平原地区低水头水工钢闸门面板的最优结构布置

钟亚丽，王 军

(上海市水利工程设计研究院有限公司，上海 200061)

钢闸门是水工枢纽的重要构成部分，在水工建筑物总造价中一般占10%～30%，在江河治理工程上甚至达到50%以上[1]，很大程度上决定了整个水利枢纽和下游人民生命财产安全。闸门结构合理布置是实现闸门结构全局最优的基础，是确保闸门整体结构经济性和安全性的重要保障[2]。李佳子[3]从闸门可靠度角度出发，指出可靠度分析是保证水工闸门良好运行的重要方法，其中一项重要指标就是了解钢闸门的荷载等相关信息。张雪才[4]等从水工钢闸门主梁的梁高优化出发，构造一个最新数学模型可以实现主梁的梁高最优。许志刚[5]等利用双拱的力学特性，闸门承受水压力受力均匀，研究了新型大跨度双拱门门体结构、拱脚结构，并根据不同运行工况对闸门进行了空间有限元分析。孙琳[6]利用NASTRAN有限元分析软件对平面钢闸门主梁、次梁作了三维有限元分析。袁宝珺[7]针对闸门流激振动进行了数值模拟计算，进而优化闸门结构设计。李国宁[8]等根据三维参数化设计的理论基础，总结了水工钢闸门三维参数化设计的优缺点和关键技术。张飞[9]对新型上下翻转弧形钢闸门设计、施工中的要点及难点的应用条件进行细致分析，对今后的工程实际应用具有良好的参考价值。王辉[10]等运用MATLAB语言采用遗传算法的方式对开敞式水闸结构进行优化设计。许世刚[11]等采用一种基于分流机制的新型遗传算法，结合水利优化设计模型，对新型方法进行了验证。仇强[12]等运用遗传算法对平面钢闸门进行了优化设计。卓美燕[13]通过对中小型钢闸门的平面体系和空间体系进行应力比较设计，优选出钢闸门面板优化设计的最佳设计方法采用规范[14- 15]的方法。

水工钢闸门的型式有平面闸门、弧形闸门以及人字闸门等。平面钢闸门具有结构形式简单，运输、安装和制造比较简便等优点。本文以平面钢闸门为例研究面板的受力情况。平面钢闸门的门叶结构形式多按孔口形式及宽高比布置双主梁或多主梁形式；闸门面板均采用梁板式结构。其中，次梁的结构布置决定了每块面板的受力情况。而整个钢闸门面板材料用量最大，成本最高。因此，如何让梁与梁之间各块面板受力均匀，是本文研究的关键。从受力机理上看，整个闸门区格被水平向主次梁及竖向隔板分为不同区格，从上到下各区格所受的水压力均不同。一般来说，面板重量占整个闸门重量的90%左右，闸门面板为整板，所以有必要通过主次梁和隔板布置，尽量使得各区格面板的应力均匀。

综上考虑，以典型平面钢闸门为例，通过合理的布置主梁后，构造一个次梁位置纠偏数学模型。保持面板经济厚度的基础上，使得各梁格之间的面板强度均匀，达到优化效果。本文以张泾河南延伸整治工程平面钢闸门为例，根据实际水头计算压力荷载，比较经过梁格布置优化的面板安全富余度提高了多少，其中安全富余度=((|优化后面板最大承受应力-最大允许应力|)/|传统方法面板最大承受应力-最大允许应力|-1)×100%，面板最大允许应力=1.1σ。

1 水工钢闸门结构布置

在一般的工程设计中，闸门结构多采用结构力学按平面体系设计方法，本文也按此设计方法进行梁格布置，梁高采用复式布置和齐平连接，水平次梁穿过横隔板上的预留孔并被横隔板所支撑，水平次梁为连续梁，其间距应为上疏下密，使面板各区格所需要的厚度大致相等，梁格布置的具体示意图如图1所示。

图1 结构布置示意图

2 优化问题的数学模型

在工程设计中，对于设计师来说，常遇到的是当工程造价一定的情况下，如何合理进行结构优化，以达到安全富余度上最优。平面钢闸门的门体主要由面板、主梁、水平次梁和横隔板等部分组成，从受力来看，面板被水平方向上的主梁和水平次梁以及垂直方向的横隔板划分成多个区格，受力特点为承受面荷载的四边支承的双向板。横隔板多按经验均匀间距布置。对于平原地区低水头钢闸门，从上到下，水压力呈三角形或梯形变化，水平次梁位置布置应采用上疏下密的形式，但具体设计时，因为各区格强度不均匀，受力较小的区格面板强度安全富余度较大，导致不合理，需进行优化，保证各区格的强度均匀，需要优化梁格布置。对于平原地区，低水头钢闸门来说，目前多采用试算法，首先拟定各梁位置，再计算各区格的面板强度，最大强度小于允许值，即认为通过。按试算法布置，计算工作量大，效率低。本文通过面板高度分布的分析模型，找其与区格位置(如图3闸门面板区格布置图所示)水压力强度的关系，运用MATLAB语言，通过纠偏函数调节水平次梁的位置，再根据目标函数的判定，使得面板受力均匀。

为了进一步阐述本文实现的技术手段、创作方法、达成目的与功效易于明白了解，笔者结合以下流程图(如图2所示)对本工程实例所采用的无偏估计法加以说明。

平原地区低水头钢闸门多采用双主梁，本文只论述次梁布置的影响。

图2 流程图

2.1 设计输入

设计输入条件包括上游侧水头Hs，下游水头Hx，闸门高度H，孔口宽度Bzs以及钢材允许应力值σ。

通过主梁的根数为x主梁根数，主梁上翼缘宽度为x主梁上翼缘宽，主梁上翼缘厚为x主梁上翼缘厚，主梁高度为x主梁高度，主梁腹板厚为x主梁腹板厚，主梁下翼缘宽为x主梁下翼缘宽，主梁下翼缘厚为x主梁下翼缘厚，等参数计算主梁应力强度，从而确定主梁位置；再根据闸门面板厚为x闸门面板厚，横隔板的根数为x横隔板根数等参数确定不同区块处，水平次梁的应力强度及位置，并判断水平次梁的应力强度及面板的应力强度是否满足。

2.2 构造数学模型

构造数学模型，其目的给水平次梁一个初始位置，如：

n=m0.688

(1)

式中，m—各区格上下位置处的水压力强度比值；n为大于1的值，是一个面板高度分布的分析模型，根据区格内水平次梁的根数，面板高度分布存在这样的一个关系1∶n∶n2…，0.688为对于低水头钢闸门最优解。

构建这个模型的目的主要是找到一个面板区间高度与水压力强度比值的关系。假设此区格间水平次梁的根数为2，如图3所示，以第二区格为例，两根主梁之间的距离定义为h，两根水平次梁将面板分成三块，将h按照1∶n∶n2划分，多根水平次梁时，按此规律划分。

图3 闸门面板区格布置图

令3面板高度为

a1=1/(1+n+n2)×h

(2)

4面板高度为

a2=n/(1+n+n2)×h

(3)

5面板高度为

a3=n2/(1+n+n2)×h

(4)

2.3 纠偏函数

纠偏函数：

(5)

式中，σi—面板应力。

区格内面板应力均值与此面板应力的比值来调整水平次梁的位置，通过纠偏函数多次迭代后，从而使得目标函数达到要求，最终确定水平次梁位置。

2.4 目标函数

目标函数：

std(σi，0)0.5<0.2

(6)

该公式表示无偏估计的应力样本标准差。标准差用来度量一组数据平均值分散程度。算出σi的标准差，其中σi表示面板的应力，是一个一行两列或多列的矩阵，0表示标注公差时要除以n-1，其目的是让这组应力平均值分散程度小于0.2。利用纠偏函数，在MATLAB应用程序中循环多次后，总会找到这样一组值，使得区格内的面板受力均匀。

3 无偏估计法与传统方法的比较

张泾河南延伸整治工程位于金山区金山新城，位于上海市水利分片综合治理的“浦南东片”，主要由一条新开挖河道和一座出海泵闸组成，工程北接卫城河，南通杭州湾，建成后将成为浦南东片南排杭州湾的通道之一。工程建设内容包括新建一座泵闸(泵闸流量90m3/s，水闸总孔径30m)以及相关配套设施。该工程节制闸为三孔，单孔净宽为10m，总净宽30m。闸门选型采用潜孔式平面直升门，闸门制作材料采用Q345钢，高度为5.5m，宽度为9.94m，小于孔口尺寸60mm，便于闸门安装、检修。梁系为实腹式双主梁结构，主梁高度为1500mm，为变截面形式。水平次梁、顶梁和底梁均采用型钢。纵向设五道竖直隔板，兼做竖向次梁。为减小阻力，启闭过程平稳、灵活，闸门采用滚动式行走支承，在两侧边梁上各安装两个悬臂滚轮。圆柱滚轮与门槽轨道采用线接触，使其运行平稳。滚轮直径800mm，材料为铸钢。闸门顶止水为P形橡皮，底止水和侧止水为条形橡胶止水，门槽宽810mm，深400mm。滚轮轨道采用工字型钢与角钢焊接截面，材料采用Q345钢。

笔者以张泾河南延伸整治工程中的节制闸为例，论述采用无偏估计法水工钢闸门梁格布置情况，并与传统方法进行比较。

本工程主梁采用实腹式双主梁，输入条件包括上游侧水头Hs=6.87m，下游水头Hx=2.5m，闸门高度H=5.5m以及钢材允许应力值σ=225MPa，主梁的根数为x主梁根数=2，主梁上翼缘宽度为x主梁上翼缘宽=0.14m，主梁上翼缘厚为x主梁上翼缘厚=0.02m，主梁高度为x主梁高度=1m，主梁腹板厚为x主梁腹板厚=0.01m，主梁下翼缘宽为x主梁下翼缘宽=0.034m，主梁下翼缘厚为x主梁下翼缘厚=0.02m，闸门面板厚为x闸门面板厚=0.008m，边梁翼缘宽为x边梁翼缘宽=0.3m，边梁翼缘厚为x边梁翼缘厚=0.014m，边梁腹板厚为x边梁腹板厚=0.01m，横隔板的根数为x横隔板根数=3。

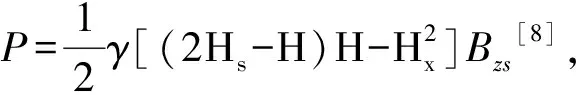
图4 水压力图

两根主梁将整个面板分为三个区格。闸门面板最底部到下主梁的位置为第一区格，下主梁到上主梁的位置为第二区格，上主梁到闸门面板最顶部为第三区格。

根据已知条件，可求得，第一区格，需布置1根水平次梁，第二区格，需布置2根水平次梁，第三区格需布置1根水平次梁。各区格水平次梁的应力见表1。

第一区格，1水平次梁高程位置在0.625m，1面板的应力为121.01MPa，2面板应力为88.29MPa，经上述的优化数学模型后，1水平次梁的高程位置在0.569m，1面板的应力为103.21MPa，2面板应力为103.21MPa。在第一区格，运用优化数学模型后，面板的安全富余度增加了32.37%。

第二区格，3水平次梁高程位置在1.898m，4水平次梁高程位置2.713m，3面板的应力为154.2MPa，4面板应力为134.99MPa，5面板应力为92.10MPa；经上述的优化数学模型后，3水平次梁的高程位置2.048m，4水平次梁高程位置在2.847m，3面板的应力为128.72MPa，4面板应力为128.72MPa，5面板应力为128.72MPa。在第二区格，运用优化数学模型后，面板的安全富余度增加了116.88%。

第三区格，6水平次梁高程位置在4.375m，6面板的应力为98.87MPa，7面板的应力为58.82MPa；经上述的优化数学模型后，4水平次梁高程位置为4.55m，6面板的应力为85.68MPa，7面板应力为85.68MPa。在第三区格，运用优化数学模型后，面板的安全富余度增加了17.10%。

在造价相同的情况下，张泾河节制闸整块面板的安全富余度增加116.88%，水平次梁的安全富余度增加了59.82%。

结合表1梁及面板应力强度分布表和图5面板应力与梁应力优化后前后对比图可知：第一区格，1水平次梁位置下移0.056m后，传统方法1面板和2面板应力强度差值为32.72MPa，优化后1面板的应力与2面板的应力相等。1水平次梁的应力没有发生变化的原因是由于下主梁的位置位于下游水位Hx=2.5m，第一区格荷载分布图属于矩形荷载，而水平次梁的荷载只与水平次梁水压力面积中心的水压力强度和区格的高程有关，二者都没有变，因此水平次梁的应力不变。

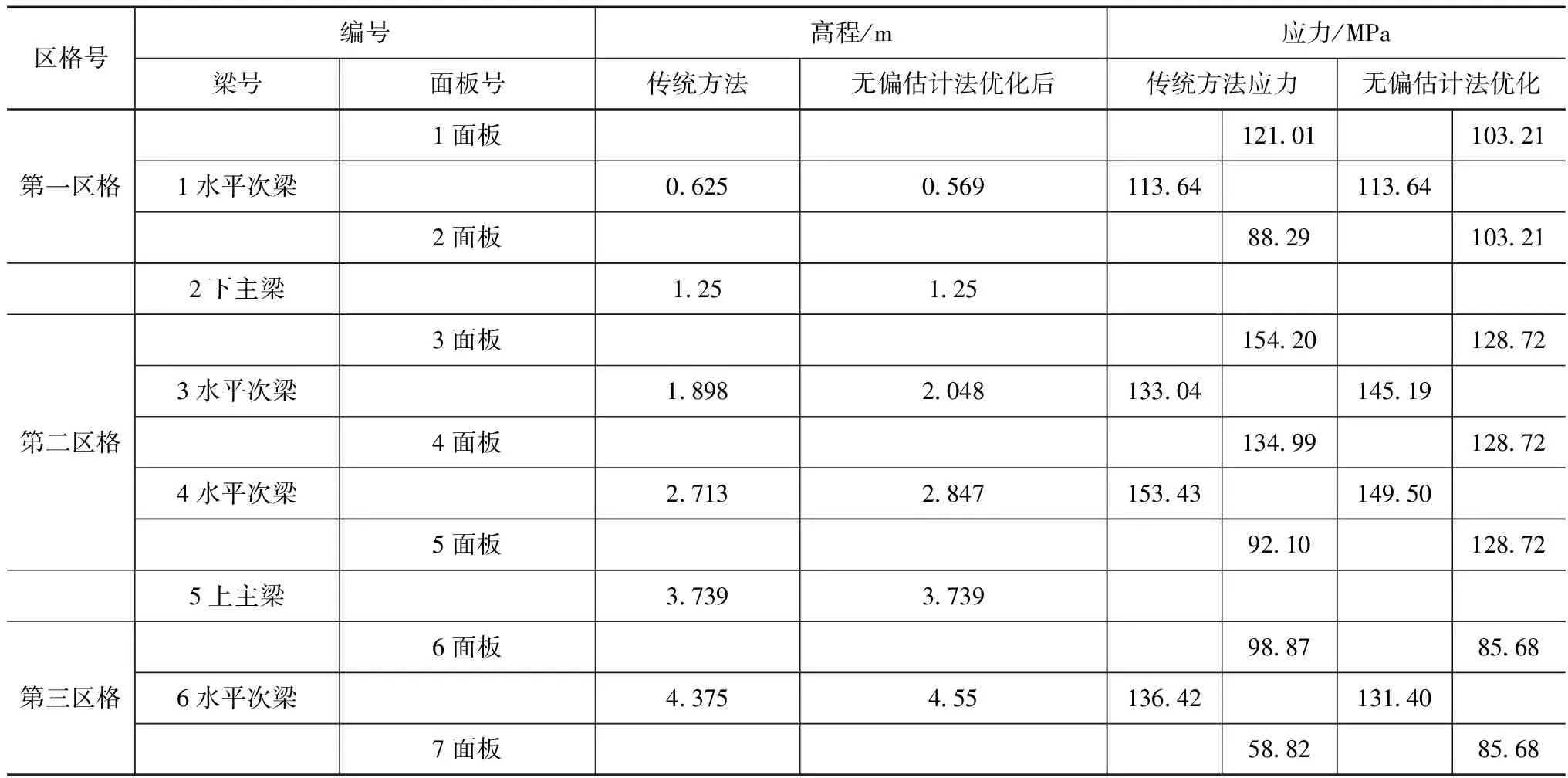
表1 梁及面板应力强度分布表

第二区格，3水平次梁位置上移0.15m，4水平次梁位置上移0.134m，传统方法面板应力强度差值(最大值减最小值)为62.1MPa，优化后3面板、4面板和5面板的应力相等。3水平次梁应力增大、4水平次梁应力减小，且受力也区域均匀。第三区格，6水平次梁位置上移0.175m，传统方法面板应力强度差值为40.05，优化后6面板和7面板的应力相等。6水平次梁应力减小。

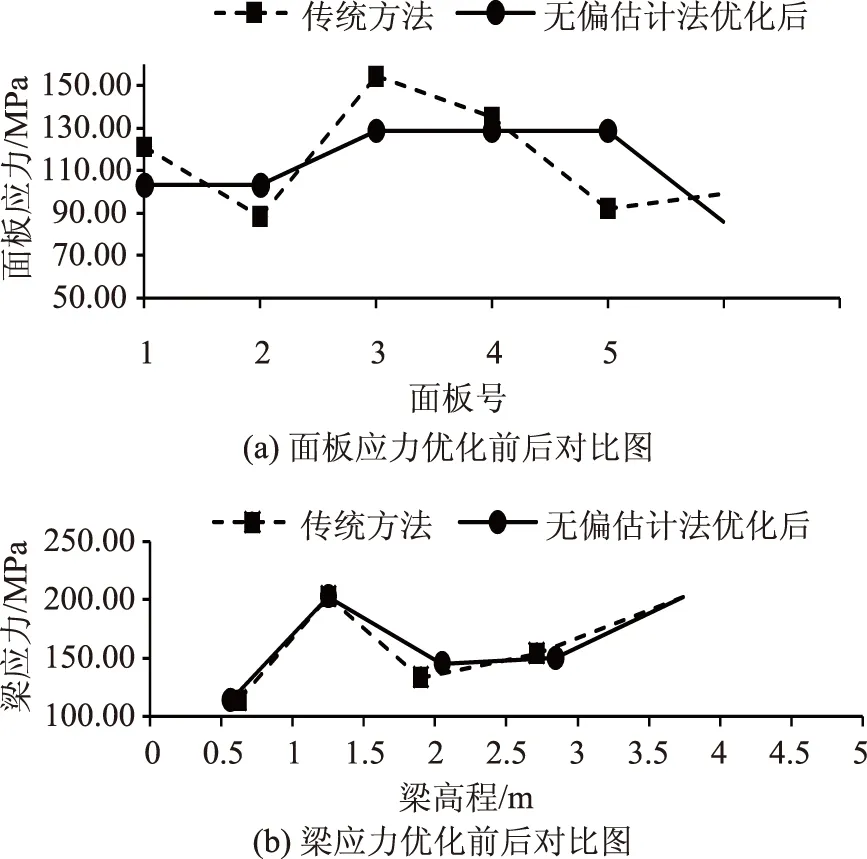
图5 面板应力与梁应力优化后前后对比图

4 结论

本文主要从闸门结构布置合理性入手，打破传统试算方法，通过编程的方式构建数学模型，优化水平次梁的位置，使面板受力均匀。在闸门面板厚度不变的情况下，从优化后的模型的可得出以下结论：

(1)利用本文采用的最优面板结构布置模型与传统方法相比较，面板安全富余度达到116.88%，各区格内的面板受力强度可以实现完全均匀，且计算方便简洁。

(2)在应力强度允许的范围内，面板材质可以采用Q235钢，减少闸门的总体造价。

公式属于根据试算结果推到得出，仍有进一步的优化空间。