基于Simulink 的GMSK 调制信号分析

张 瑾，袁韵洁，蔡晓磊，杨玉婷

（西安电子工程研究所，陕西 西安 710100）

0 引 言

通信系统中，数字调制技术作为关键技术之一，已广泛应用于数字通信系统设计及研究，其具有抗干扰能力强、易于处理等优点。相对于先前恒包络调制技术相位突变的问题，恒包络连续相位技术以其恒定包络、连续相位、频谱尽可能集中在主瓣，旁瓣滚降衰减快等适合非线性信道传输的特点应运而生。MSK 和GMSK 是恒包络连续相位调制技术的典型代表，其中GMSK 调制技术是MSK 技术的一种改进形式，因其频谱紧凑、误码性能好，在通信领域得到广泛使用[1]。

信道编码的作用主要是提高信道可靠性，降低信息传输误码率，在接收端纠正传输信息的错误，使接收端解调的信号尽可能与发送端一致。汉明码是第一个实用的差错控制编码，在一个码组只能纠正单个比特错误。常用的编码方式有RS、Turbo 等编码[2]，近年发展起来的LDPC 编码是最接近香农定理的编码方式。

1 GMSK 调制原理简述

GMSK（高斯最小频移键控）调制是在FSK（频移键控）的基础上发展起来的一种调制方法。因FSK 的相位不连续，相位连续且调制系数为0.5 的MSK（最小频移键控）调制方法由此而来，GMSK 即是在MSK 的前面加一个高斯滤波器，经过高斯滤波器的预调制滤波，交越零点处的调制信号经过平滑过滤，相位连续[3]。

GMSK 调制具备相位连续、包络恒定等特点，且由于经过高斯滤波器的预调制滤波，有效抑制了信号带外辐射。图1 为GMSK 信号调制的原理框图。

图1 GMSK 信号调制原理图

高斯滤波器的矩形脉冲响应函数g(t)为：

其中，Bb为基带带宽，Tb为基带码元间隔。

MSK 的信号表达式为：

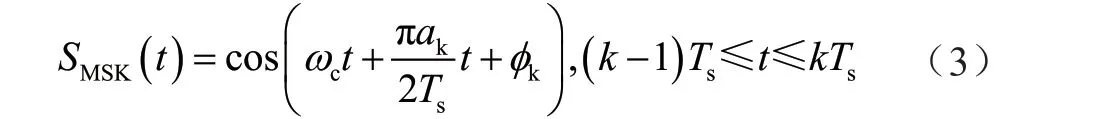
其中，ωc为载波角频率，Ts为码元宽度，ak为第k个码元中的信息，取值为±1，φk为第k个码元的相位常数，在时间(k-1)Ts≤t≤kTs内保持不变[4，5]。

由高斯滤波器的矩形脉冲响应表达式g(t)和MSK信号表达式SMSK(t)，得出GMSK 信号的表达式为：

2 GMSK 有无信道编码仿真

本设计在Matlab 仿真软件的Simulink 环境下，建立GMSK 无信道编码的硬件仿真模型，如图2 所示。其中Bernoulli Binary Generator 用于产生信息数，Buffer用于组帧，GMSK Modulator Baseband 用于进行GMSK调制，AWGN Channel 用于模拟噪声环境，可进行信噪比的设置，GMSK Demodulator Baseband 用以实现GMSK 解调；Buffer1 用于将解调后的信号由一帧数据变成一位一位的输出便于与Bernoulli Binary Generator产生信号比对；Error Rate Calculation 用于对比解调后信号与原始信号并输出误码率；Display 用于显示误码率；Scope 用于在时域观察对比原始信息与解调后信息。

图3 为GMSK 加 入LDPC 信 道 编 码 的Simulink实现框图，在GMSK 调制前加入LDPC Encoder，在GMSK 解调前先进行解码，即加入LDPC Decoder 模块。LDPC 码具有非常稀疏的校验矩阵，矩阵的行重、列重远远小于码长，且任意两行或者两列最多只有一个相同位置的1[6]。LDPC 码的译码算法根据传送消息的不同形式，分为硬判决议码和软判决议码两大类。目前主要的硬判决译码算法简单，译码速度快，易于硬件实现，但其纠错性能差。软判决议码算法主要有基于迭代结构的置信传播算法（BP）和后验概率（APP）译码等算法，应用较为广泛的为置信传播算法[7]。

图2 GMSK 无信道编码的硬件实现框图

图3 GMSK 有信道编码的硬件实现框图

在数字系统中，误码率和频谱性能是衡量可靠性的主要指标，本系统在Simulink 下进行仿真，通过AWGN Channel 修改信道信噪比， 在Error Rate Calculation 模块得到误码率，如图4 所示。由图4 可知，GMSK 调制信号在AWGN 信道下的误码率，随着信噪比的增加而降低，并且GMSK 加LDPC 信道编码相对于GMSK 无信道编码达到的传输效果要好。

在实际场景中，因无线信号在空中传播，无法避免多径效应的产生，因此本系统设计用Multipath Rayleigh Fading Channel（瑞利衰落信道）模拟多径效应。在AWGN Channel 前面加入Multipath Rayleigh Fading Channel 模块模拟，并且通过AWGN Channel 改变信噪比。通过图5 中GMSK 与GMSK+LDPC 在瑞利衰落信道下的误码率对比可知，在传输信息很长的情况下（＞104）GMSK 加LDPC 信道编码达到的传输效果最好，传输误码率最小。

图4 GMSK 与GMSK+LDPC 在AWGN 信道下的误码率对比

图5 GMSK 与GMSK+LDPC 在瑞利衰落信道下的误码率对比

3 结 论

本文对GMSK 调制信号进行了研究，将算法转换成硬件可实现模块，通过Simulink 对GMSK 有无信道编码进行硬件仿真建模，并对设计进行仿真验证，分析在不同信道下对信息传输误码率的影响。该设计具有实现简单，容易实现数字化的优点，能够与其他模块一起实现最终的大规模指令传输系统的集成。