基于贪心策略的环形穿梭车调度算法设计

◆邹佰翰 夏 鑫 张吉懿

（1.天津工业大学 天津 300387；2.华北水利水电大学 河南 450000；3.郑州航空工业管理学院 河南 450046）

1 环形穿梭车系统概述

最经典的环形穿梭车系统，由环形轨道、N 辆穿梭车、m 个进货口构成。A 侧进出货口是出货口在一起，进货口在一起；B侧进出货口交替排列。小车的起点都位于A 侧直轨道的正中间，即有如下示意图1：

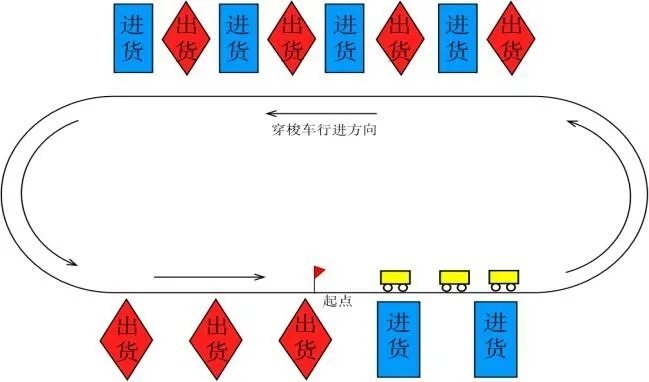
图1 环形穿梭车示意图

系统需求即需要确定使系统效率最高的环形穿梭车的数量和调度方法。

2 问题分析

在此将在同一时间区间内处于同一直轨道上的穿梭车集合视作一个队列。以贪心策略建立模型，选取评估参数，使用数据包络分析法（DEA）输出最优目标值。

3 模型的建立与求解

3.1 环形穿梭车运动基本模型的建立

贪心策略是基于贪心选择的算法，指在对问题求解时，总是做出在当前看来是最优选择每做一次贪心选择就将所求问题简化为一个规模更小的子问题。

对于穿梭车在相邻的两个装/卸货口之间的运行时间t，有如下公式：

（1）对于任意穿梭车s 的装卸路线，可总结以下方法：当穿梭车前面的车数为0，即穿梭车位于队首，需前往最远的货口。

（2）如果距离d大于相邻两装/卸货口之间的距离，则需要依据如下具体情况判断：

在A 侧：若对几个装/卸口均分穿梭车，则相邻两装卸口之间的距离无法容纳相应数量的穿梭车。此时穿梭车应当停留在最近的货口。

在B 侧：当相邻两穿梭车装载任务相同，且都是空车或都满载的情况下，不能继续前进。此时穿梭车必须停留等待，此时前往最近的货口。

为使总完工时间最小，提出如下目标函数：

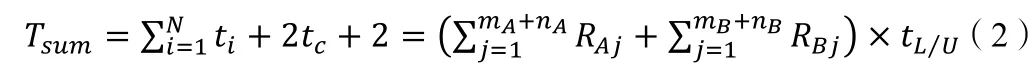
3.1.1 当穿梭车s 位于队首

在当前直轨道上，假设穿梭车s 前面的车的数量Pns=0。若穿梭车s 后面的车数Pbs＞0，即穿梭车的后面还有其他车：

① 若此时穿梭车从B 向A 运载，且满足如下条件：

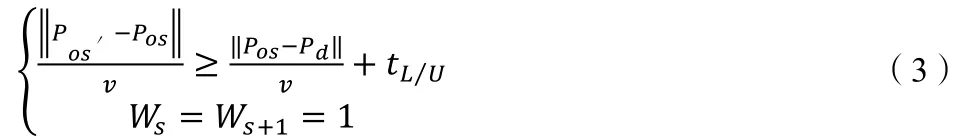
此时，穿梭车s 可以就近停在距离它最近的装货口。

②若穿梭车同样是从B 向A 运载，但满足如下条件：

此时与①中情况相反，穿梭车s 应前往距离它最远的货口。

3.1.2 穿梭车s 位于队列中间或队尾

假设前面的车数Pns＞0，考虑穿梭车在队列中间或者队尾的情况：

（1）当穿梭车从B 侧向A 侧运载时，根据排队论，对于每个装/卸货口，按顺序分配n′

辆穿梭车。从而可得到穿梭车s 的运动规划：

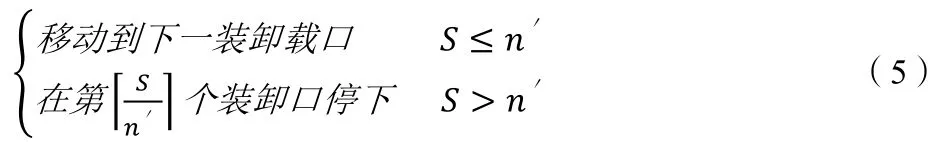
（2）当穿梭车从A 侧向B 侧运载时：

①若载货的穿梭车到达指定的卸载口，则所需时间满足递归公式：

②若穿梭车空车到达装载口，且其后面的穿梭车s-1 的任务是卸货，则穿梭车只需就近装载。这一过程可用流程图表示如图2：

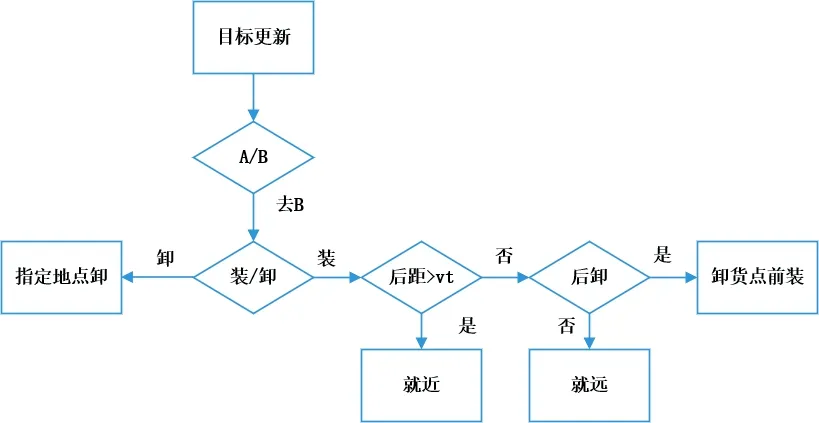
图2 去往B 侧的示意图

3.2 对系统效率的评估

为确定系统工作效率，在此运用数据包络分析法对系统效率做出评价。各项评估指标如下：

（1）拥堵时间：按所有穿梭车拥堵的时间总和来计算。设穿梭车s 在第j个货口附近消耗的拥堵时间为Tsj，则总拥堵时间Tsum为：

（2）穿梭车数量：穿梭车队列的总长度不能超过环形轨道的周长。即应当做如下约束：

将数据导入Lingo 得到效率指数如表1：

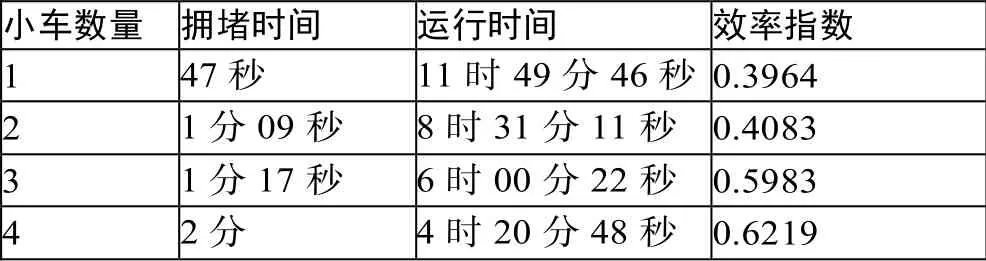
表1 效率指数表

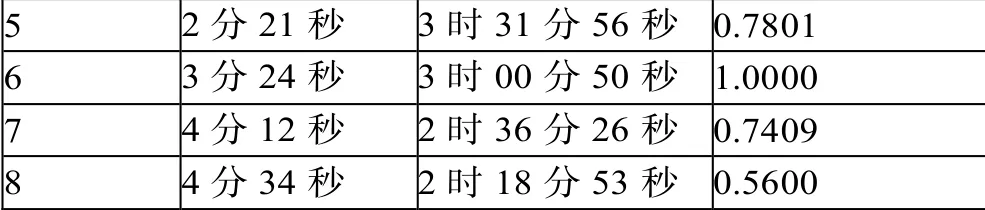
5 2 分21 秒 3 时31 分56 秒 0.7801 6 3 分24 秒 3 时00 分50 秒 1.0000 7 4 分12 秒 2 时36 分26 秒 0.7409 8 4 分34 秒 2 时18 分53 秒 0.5600

从表中可以看到在穿梭车数量区间[2，6]内，效率指数经历了稳定上升的过程。当小车数量超过6 时，在[6，8]区间内，系统的效率指数开始变得不再稳定。

综上，我们认为系统整体的运行效率较高，系统中的小车数量在6 辆左右时效率较高，但出于安全性和稳定性的考虑，小车数量不能高于8 辆。