多站交叉定位相对GDOP及其测向站分布问题研究

罗双喜

(江苏自动化研究所，江苏 连云港 222061)

被动组网探测系统能够联合利用多个站点的角度测量信息,实现对目标的定位。常用的定位方法包括多站测向定位、多站测时差定位和测向—测时差联合定位等。因为对侦察设备要求相对简单,测向交叉定位方法在测向站网络、电子侦察等方面得到了广泛的应用,定位算法已发展成熟。

众所周知,在交叉定位系统中,目标与测向站之间的相对位置分布对定位精度有重要影响。因而GDOP分析与测向站(测向站)优化配置是交叉定位理论的重要研究内容。国内外对两个测向站的情况研究较多,例如文献[1]对交叉定位误差相对几何稀释度进行了研究并得到了一些结果;文献[2-3]从交汇角的角度对定位精度进行了分析，文献[4-5]对测向站的最优分布问题进行了研究,对多个测向站的情况则很少涉及,这正是本文将要重点关注解决的问题。

考虑m(m≥2)个测向站纯方位交叉定位问题

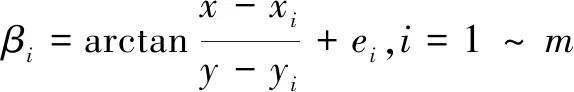
(1)

其中,(xi,yi)T为第i个测向站的位置,βi和ei为第i个测向站的方位测量值和测量噪声。根据Fisher信息理论,定位误差协方差矩阵的克拉姆—劳下界(CRLB)P的逆矩阵就是其信息矩阵[1]:

(2)

其中,ri为第i个测向站到目标的距离(i=1～m)。

对于两个测向站的情形,定位误差方差为

(3)

其中,Tr(P)表示误差方差矩阵P的迹。

(4)

其中,α1和α2为定位三角形中两个测向站所在顶点对应的三角形内角,如图1所示。

根据式(3),RGDOP达到最小的必要条件为

(5)

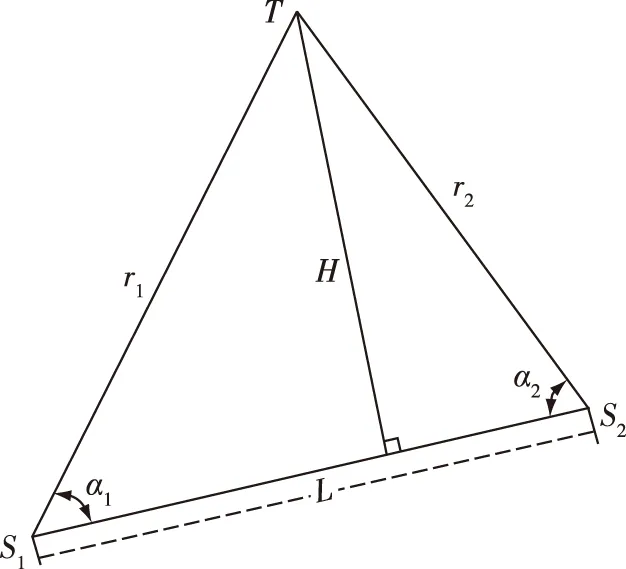
图1 两个测向站交叉定位示意图

进一步分析表明,方程组(5)有唯一解(sin2α1是某个三次多项式的特征根)。

1 两站交叉定位RGDOP分析

从式(4)可以看出,两个测向站与目标连线之间的夹角越小,定位误差越大。为保证足够的交叉定位精度,通常要求参与定位测量的两个测向站不能相距太近。因此,可以采用两个测向站之间的距离L代替H来定义RGDOP。

如图1所示,在定位三角形中,根据正弦定理可知

(6)

记f(α1,α2)=L-2Tr(P),则最小RGDOP问题可表示为如下形式的极小化问题:

(7)

该问题的最优性必要条件为

(8)

当比值λ在开区间(1/2,2)之内时,式(7)的最优解由比值λ唯一确定:

(9)

(10)

即测量误差大的测向站所对应的定位三角形的内角也大。

当λ∈(1/2,2)时,f(·,·)的最小值可表示为

(11)

其中,φ(λ)是目标函数中分母项的倒数:

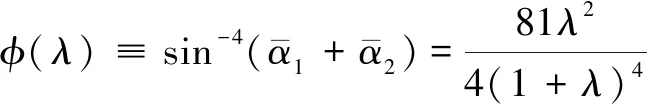
(12)

函数φ(λ)在λ=1时取得最大值,在λ=1/2和λ=2时达到最小值1,如图3所示。

图随λ变化曲线

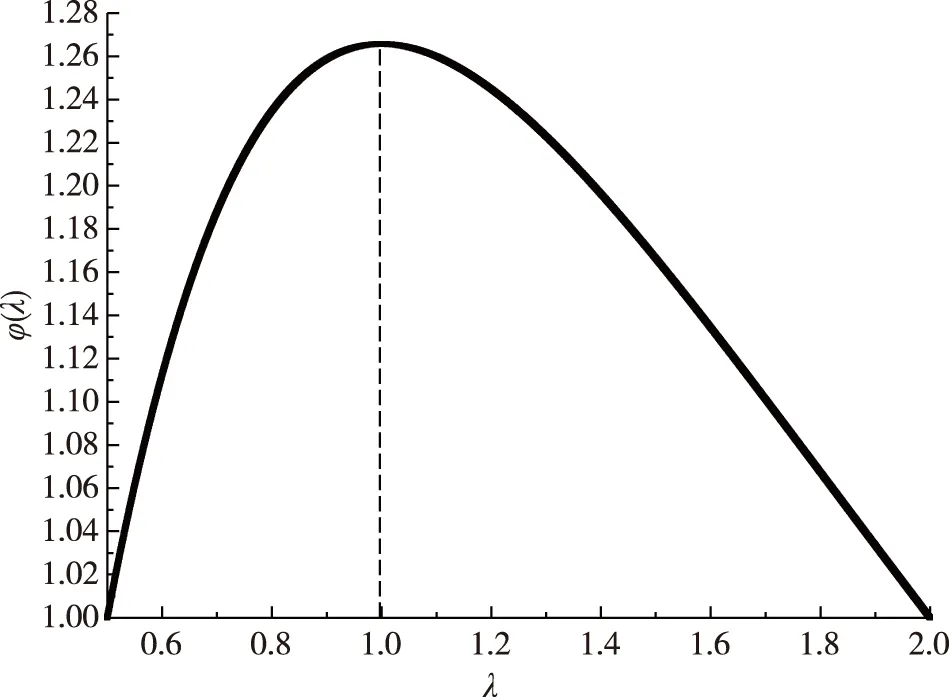
图3 φ(λ)-λ变化曲线

综上所述,优化问题(7)的最优函数值为

(13)

2 多站RGDOP分析与测向站最优分布

如上所述,对于双站测向定位系统,可以用目标到测向站连线的距离或者测向站之间的距离来定义RGDOP。对于这两种情况,理论上均可得到最小RGDOP值所对应最优解的解析表达式。但这两种定义所采用的距离量都是利用三角定位原理计算出来的;对于多个测向站的情形,可计算得到的距离量不是唯一的,因此这两种定义均难以推广应用于多站交叉定位系统。

对于形如式(1)的m个测向测向站的交叉定位问题,其定位误差方差(下限)为

(14)

其中,

(15)

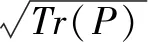
式(2)中,分子项可看作两个距离量的平方的加权值。一个自然的思路就是采用如下定义的加权距离来定义RGDOP

(16)

对于两个测向站的情况,从式(2)可以看出,当且仅当两条方位线相互垂直时达到最小RGDOP值。对于多测向站的情况,此时有

(17)

显然,此时最小RGDOP问题等价于式(17)右侧表达式分母的极大化问题。进一步分析可以发现,该优化问题存在鞍点,但不是最(极)大值点。

仔细观察式(14)的表达式,可利用如下形式的加权距离来定义RGDOP

(18)

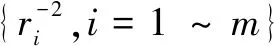
将交叉定位均方误差与距离R的比值作为相对几何稀释度,立即得到

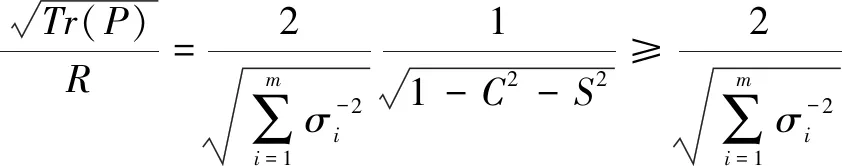
(19)

等号成立的充要条件为C=S=0,即

(20)

下面按测向站个数分两种情况进行分析。

1)两个测向站

对于两个测向站的情形,容易导出式(20)的等价形式

(21)

其中,第一个条件意味着两个测向站到目标的距离与其方位测量精度的乘积相等,第二个条件表示两个测向站与目标的连线相互垂直。

2)多个测向站

对于多个测向站的情形(m>2),方程组(20)含有2m个未知变量、2个方程,因而方程组是欠定的,通常情况下有很多解。下面的例子说明,其最小RGDOP值是可以达到的。

假设m个测向站(测向站)的分布满足条件

(22)

其中,θ=2π/m,δ为任意正常数。

式(22)中,第一个条件表示各测向站按方位“均匀”分布于以目标为中心点的各方向上;第二个条件表示测向站到目标的距离与该测向站的方位测量精度的乘积为常数。此时di=m-1(i=1～m)且有

(23)

即式(20)成立,从而达到最小RGDOP值。

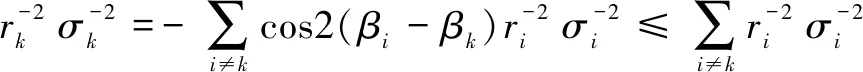
(24)

上式表明,仅在某些特定条件下,方程组(20)可能无解,例如{ri,i=1～m}已知且存在k使得不等式(24)不成立时。下面对这种条件下的最优RGDOP值及相应的测向站分布问题进行分析。

根据式(19)可知,最小RGDOP问题等价于极小化问题:

(25)

1)函数g(β1,…,βm)的角度“平移”不变性

容易验证,各测向站的方位测量值发生”平移”后,g(β1,…,βm)的函数值保持不变,即

g(β1-α,…,βm-α)=g(β1,…,βm)

(26)

其中,α为任意实数。

2)最优函数值的范围

因为方程组(20)无唯一解,所以式(25)中的最小值大于零。另一方面,取

(27)

(28)

由此可见,最优函数值在开区间(0,1)之内。

3)最优RGDOP值及测向站分布

(29)

(30)

(31)

(32)

其中,Δ⊂{1～m}表示Δ为{1～m}的任意真子集。

反之,若Δ0是式(32)右侧组合优化问题的最优解,取

(33)

(34)

根据式(32)与(34),可知

(35)

相应的最优RGDOP值为

(36)

从上述分析过程可以看出,当测向站与目标之间的距离给定且方程组(20)无解时,最优RGDOP是式(36)右侧组合优化问题的最优值,此时所有测向站分为两组,每一组内各测向站分布于同一方位线上,两组之间的方位线相互垂直。这种测向站分布形式等效于两个测向站,相当于先将同一组内各测向站的方位测量值进行加权融合,然后利用融合后的两个方位值进行交叉定位。

3 结束语

本文首先分析了两站测向定位系统的RGDOP定义,指出用于定义RGDOP的距离量可以是目标到测向站连线的垂直距离,也可以是测向站之间的距离,或者测向站到目标的距离的加权平均值。针对常用的两个测向站几何稀释度定义难以推广到多测向站的问题,提出了一种新的基于加权距离的RGDOP定义(该距离的平方的倒数是各测向站到目标距离的平方的倒数的加权平均值)。无论是两个测向站还是多个测向站,该定义具有统一的表达形式,且具有简洁的最小RGDOP值显式计算公式,并分别给出了达到相应最小RGDOP值的充要条件和实例。当各测向站到目标的距离已知但不满足该充要条件时,给出了最小RGDOP值的计算公式和相应的测向站最优分布结果。