基于多地并行融合的多传感器目标识别信息融合方法

赵 照,吴晓锋

(闽南师范大学数学与统计学院,福建 漳州 363000)

自20世纪70年代起,多传感器信息融合技术迅速地发展起来,并且在军事和民生诸多领域得到广泛应用。根据被融合信息的属性,文献[1]将信息融合划分为数据级、特征级和决策级融合。文献[2]则将信息融合分为位置估计与目标身份识别、态势估计、威胁估计等三级。文献[3]在此基础上进一步细分了信息融合功能模型,把信息融合划分为检测级融合、位置级融合、目标识别级融合、态势估计、威胁估计以及精细处理,由此对信息融合过程做了更清晰的划分,为人们研究信息融合提供了便利。

在信息融合功能模型中,目标识别级信息融合是指对来自多个传感器的目标身份识别信息进行综合,以得到对目标身份的联合估计[4]。这些目标身份按照论域的不同,划分也不同。比如空中的战斗机、轰炸机、预警机,海上的航母、驱逐舰、护卫舰等。联合估计的目的：一是得到高质量的目标识别结果,如更完整、精确的目标身份估计[5];二是多个传感器平台之间达成一致的目标身份判断,这在自主执行任务的多机器人、协同行动的多作战平台等实际应用中尤为重要[6-7]。且目标识别级融合的传感器是可以独立识别出目标可能的身份,比如有雷达、光电、声呐等传感器。

关于目标识别的信息融合,目前有基于D-S证据理论[8-11]、基于DSmT方法[12-14]、基于贝叶斯准则[15-16]、基于贝叶斯网络[17]、基于模糊综合方法[18-19]、基于Vague集方法[20,21]、基于粗糙集理论[22]、基于决策模板[23,24]、基于属性测度[25-27]等算法。在这些融合方法中,各传感器必须分别给出每个待识别目标属于每种身份类型的基本概率函数、先验概率和条件概率、模糊隶属度、灰关联度等,再采用一定的组合规则(如Dempster组合公式、贝叶斯公式等)或相似标准(如决策模板或属性标准矩阵等),对获得的多个目标识别结果进行融合和综合判断。

上述方法都是讨论多传感器的目标识别信息集中到某个融合中心进行信息融合,适合于基于融合中心的目标识别信息融合结构。与此不同,本文提出了一种多地并行融合的分布式目标识别信息融合方法,由嵌入在每个传感器的融合模块通过接收邻居的目标识别信息并进行融合,然后把融合的目标识别信息传递给它的邻居,继续循环下一轮的融合过程,直至在各传感器之间达到一致的目标身份识别。

1 分布式目标识别信息融合结构与融合算法

1.1 分布式目标识别信息融合方案

对于存在融合中心的信息融合来说,按照目标身份识别的一般过程,可以产生三种不同融合结构:数据层融合、特征层融合和决策层融合。这里,以决策层融合结构为例,给出基于融合中心的多传感器目标识别信息融合结构,如图1所示,其中,每个传感器的目标处理过程类似于图中所示的传感器平台i的目标处理过程。

图1 基于融合中心的多传感器目标识别信息融合结构

基于融合中心的目标识别信息融合结构是与集中式指挥与控制相匹配的,它具有构造简单、组织方便等优点,但存在隐蔽性差、生存能力脆弱、通信能力要求高、信息融合质量易受干扰影响等弱点。

现在考虑一种多地并行融合的分布式目标识别信息融合结构,在每个可独立发现和识别目标的传感器上都配置两个模块:本地目标识别模块和本地融合模块。在这里,每个传感器只与它的通信范围内的部分传感器(称为“邻居”)进行目标信息交换,如图2所示。

分布式目标识别信息融合结构可以克服基于融合中心的目标识别信息融合结构的缺点,并且具有拓扑结构简单、传感器之间的通信距离可缩短等优点。我们需要解决的问题是:如何设计一种在每个传感器运行的融合算法,使得在一定的传感器网络拓扑下,各传感器得到一致的目标身份信息。

图2 多传感器分布式目标识别信息融合结构

1.2 分布式融合算法模型

假设有N个分布在不同区域的传感器Vi,i=1,2,…,N,传感器集合记为V={V1,V2,…,VN}。不失一般性,考虑单目标的身份识别问题。假设目标可能有M种身份,表示为B={b1,b2,…,bM},它亦称为识别框架。

对于识别框架B,令2B={b1,b2,…,bM,{b1,b2},{b1,b3},…,{b1,bM},{b2,b3},…,{b2,bM},…,{b1,b2,…,bM}}为B的幂集(本文不考虑空集),即B的所有子集所构成的集合。幂集2B表示目标的所有身份可能(包括同时属于多种身份)。

假设每个传感器对目标识别信息的融合过程可以划分为序贯、一致有界的无限时域序列qk=[tk,tk+1],k=0,1,2,…,在每个时域qk内,每个传感器与邻居之间进行一次信息交换,并且对来自邻居的目标识别信息进行融合。

根据D-S组合原则,可以按如下公式求得融合后的目标识别信息

∀Qi,Qj∈2B,

(1)

其中,

∀Qj∈2B。

(2)

如果上述Ki(k-1)=1,传感器i在时域qk上将不能获得融合结果{mi(Qi,k),Qi∈2B}。

根据算法(1)(2),传感器i在给定时域qk内的融合算法描述如下。

传感器i的融合算法 1. k=0时,传感器i获得初始目标识别信息{mi(Qi,0),Qi∈2B},并将该组信息发送给所有接信邻居j∈Nouti;2. 对接收到的送信邻居传递来的目标识别信息{mj(Qj,0),Qj∈2B,j∈Nini}与本地目标识别信息{mi(Qi,0),Qi∈2B}进行数据关联;3. 由算法(1)(2)得到目标识别信息的更新状态{mi(Qi,k+1),Qi∈2B};4. 发送更新后的状态{mi(Qi,k+1),Qi∈2B}给接信邻居传感器j∈Nouti;5. 如果对任意i,j∈V,有mi(bm,k+1)=mj(bm,k+1),m=1,2,…,M,则结束运算,否则,返回到第3步。

2 仿真分析

假定传感器网络由6个传感器组成,待识别的目标有3种身份B={敌方,友方,中立方}。则B的幂集2B={敌方,友方,中立方,{敌方,友方},{敌方,中立方},{中立方,友方},{敌方，中立方，友方}}。

假设6个传感器获得的初始目标识别信息分别为:

{m1(Q1,0),Q1∈2B}={0.1, 0.1, 0.4, 0.2, 0.05, 0.05, 0.1};

{m2(Q2,0),Q2∈2B}={0.2, 0.2, 0.2, 0.1, 0.1, 0.15, 0.05};

{m3(Q3,0),Q3∈2B}={0.1, 0.15, 0.2, 0.1, 0.15, 0.2, 0.1};

{m4(Q4,0),Q4∈2B}={0.15, 0.1, 0.25, 0.1, 0.1, 0.2, 0.1};

{m5(Q5,0),Q5∈2B}={0.3, 0.1, 0.1, 0.15, 0.15, 0.1, 0.1};

{m6(Q6,0),Q6∈2B}={0.1, 0.15, 0.15, 0.2, 0.1, 0.2, 0.1}。

可看出传感器1～4的初始识别结果倾向于目标为“中立方”。

传感器网络的拓扑结构分别为链形、环形和有向树,如图3所示。

图3 三种传感器网络拓扑结构

本文利用Matlab软件对融合算法(1)(2)进行计算,得到传感器网络在三种拓扑情况下的分布式融合过程,分别如图4～6所示。

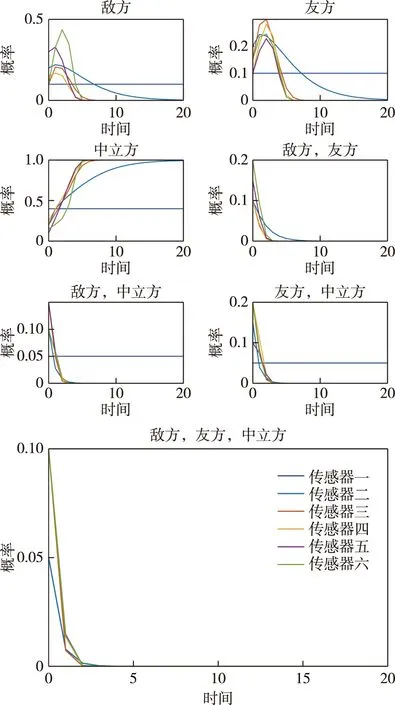
图4 传感器网络在链形情况下的分布式融合过程

从仿真中可以看出,对于链形和有向树的传感器网络,除了根传感器1之外,其他各传感器运行融合算法(1)(2)可以达到一致融合结果{m(Q,∞),Q∈2B}={0, 0, 1, 0, 0, 0, 0},即识别目标为“中立方”。对于环形传感器网络,所有传感器都可以达到上述一致融合结果。这表明,一致的融合结果倾向于各传感器的多数共识的初始目标识别意见。且易知随着传感器数量的增加,累计融合次数将会加大,算法耗时将增多。目标数量在增多时,根据D-S合成规则,目标的所有身份可能会呈指数级增长,因此，会大幅降低融合算法的速度。

图5 传感器网络在环形情况下的分布式融合过程

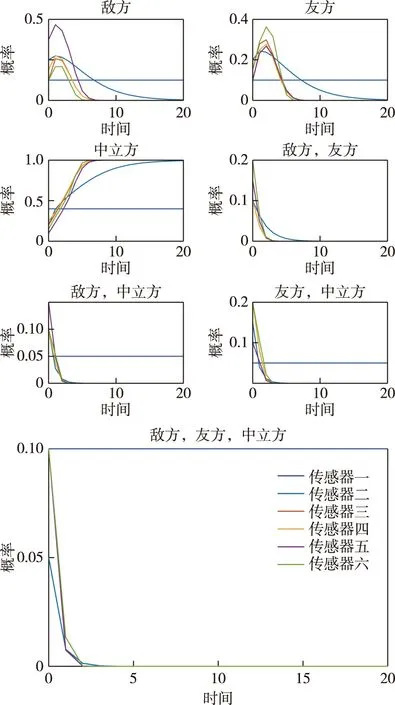
图6 传感器网络在有向树情况下的分布式融合过程

3 结束语

本文提出了一种多地并行融合、去中心化的传感器网络目标识别信息融合方案,其中,每个传感器只需要与邻居传感器交换目标识别信息。我们基于D-S证据理论,设计了一种可用于上述分布式信息融合的融合算法。在一定的传感器网络拓扑情况下,每个传感器运行该融合算法可达到一致的目标识别信息融合结果。实例仿真结果验证了该融合算法的有效性。