满足静水性要求的Jackson潜艇船型

齐 翔, 唐 晓, 齐 欢

（1. 中国舰船设计研究中心，湖北 武汉 430064；2. 空军预警学院，湖北 武汉 430012；3. 海军工程大学，湖北 武汉 430032；4. 武昌首义学院，湖北 武汉 430064）

0 引 言

潜艇具有典型的水动力学特征，其外形一般采用阻力性能较好的水滴型回转体，从而适当减小长宽比，获得更优良的总布置条件。水滴型艇型的母线线型一般采用 Jackson潜艇线型控制方程设计。杜月中等[1]分析流线型回转体外形设计的特点并研究线型拟合。陈明高等[2]研究确定常规潜艇排水量和主尺度的新方法。刘明静等[3]研究复杂回转体的数学表示方法。唐晓等[4]研究潜艇数学船型和求解形状因子的超越方程组。

1 回转体的数学表达

潜艇裸艇（主艇体，不包括指挥塔围壳、舵和鳍等附体）可分为进流段、舯段和去流段等3部分，主要设计参数包括艇长L、进流段长L1、舯段长L2和去流段长L3，其中L=L1+L2+L3。

Jackson船型有多种表现形式，一般采用两参数模型（简记为模型2）和三参数模型（简记为模型3）。

1) 对于模型2，进流段的表达式为

去流段的表达式为

式(1)和式(2)中：nh和nf为形状参数。

2) 对于模型3，进流段的表达式为

去流段的表达式为

式(3)和式(4)中：mh、nh和nf为形状参数。

通过分析Jackson模型可知，实际上可将该模型划分为四参数模型（简记为模型4）、模型3和模型2等3种，其中模型3和模型2都是模型4的特例。为详细比较这些模型在实际应用中的特点，做如下讨论。

1.1 模型4

引入形状因子α1、α2、α3和α4，回转型潜艇的回转半径函数可表示为

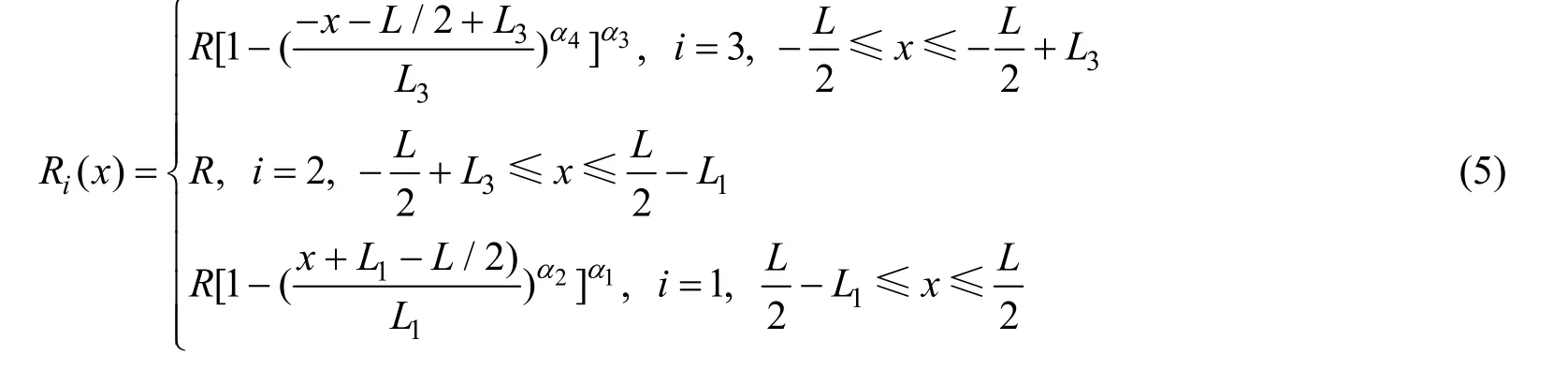
潜艇船型曲线为

在xOy平面上，潜艇进流段船型曲线（见公式（7））和去流段船型曲线（见公式（8））

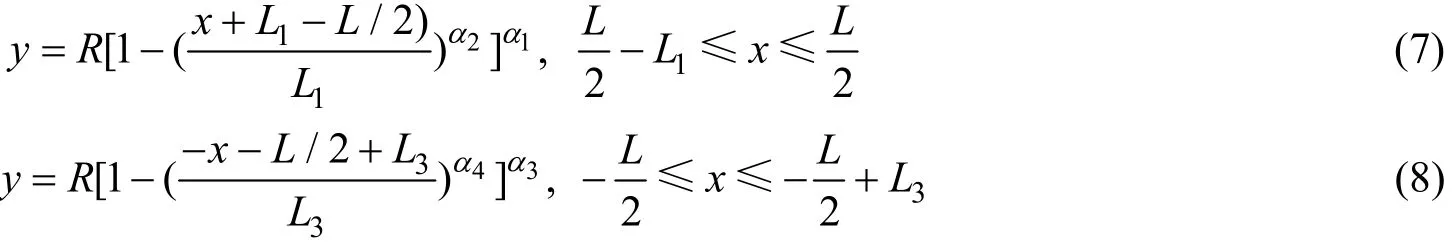
在上述潜艇的数学船型表示下，潜艇的排水量体积可表示为

潜艇的浮心纵坐标可表示为

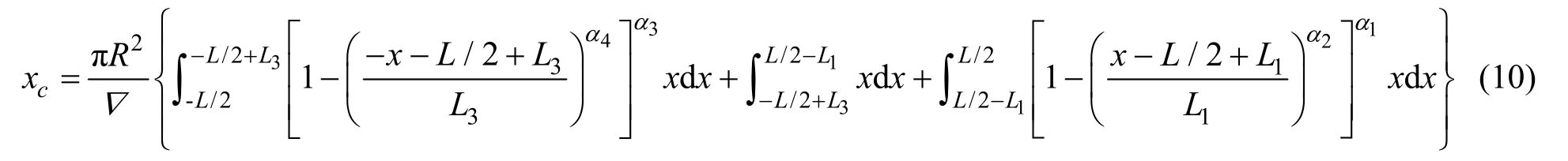
在数学船型中，由于潜艇线型是采用函数的形式表示的，可采用解析方法计算潜艇的湿表面积，有

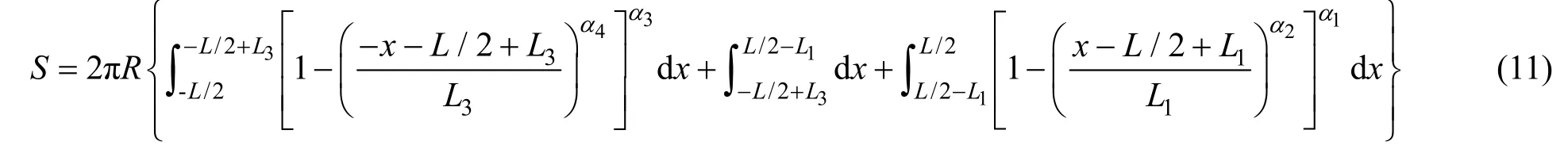
1.2 模型3

1) 模型3-1：在形状因子中，若令α4=1，则回转型潜艇的回转半径函数可表示为

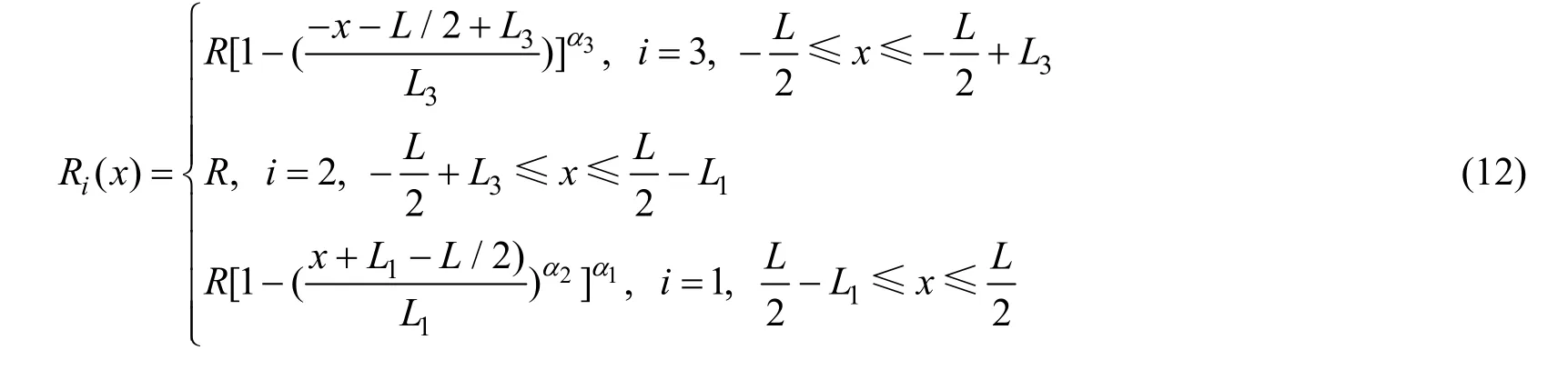
其他公式类似。

2) 模型3-2：在形状因子中，若令α4=2，则回转型潜艇的回转半径函数可表示为

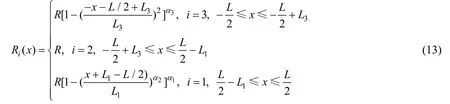
其他公式类似。

3) 模型3-3：在形状因子中，若令α3=1，则回转型潜艇的回转半径函数可表示为

其他公式类似。

1.3 模型2

在形状因子中，若令α2= 2 ,α4= 2 ，则回转型潜艇的回转半径函数可表示为

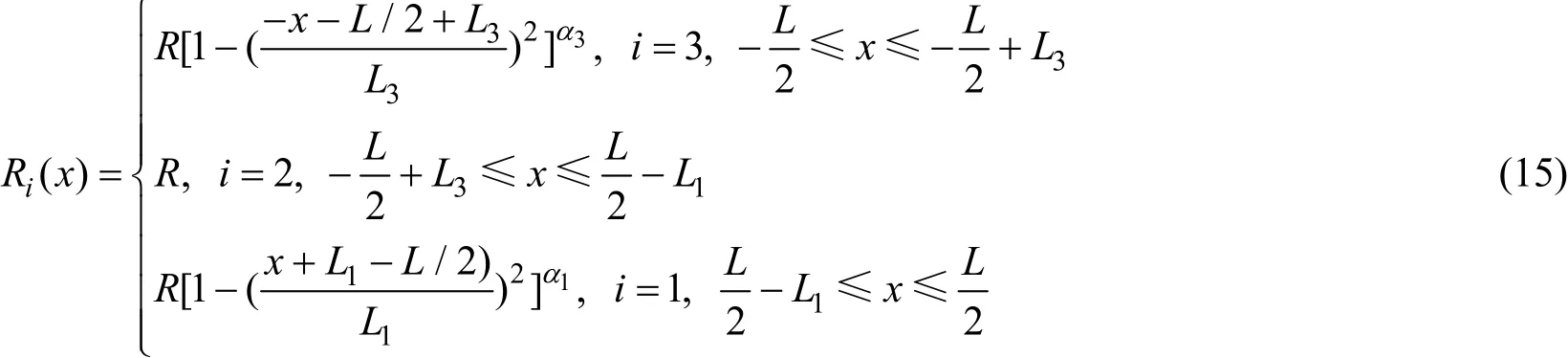
其他公式类似。

显然，参数越少越有利于进行分析和优化，不利的方面在于参数越少，调控进流段和去流段的手段越单一。设计中的一个重要问题是对二者进行平衡，在满足基本形状调节控制要求的前提下，尽可能地减少设计变量。

2 潜艇的静水性条件和船型

潜艇的静水性条件主要指排水体积和浮心纵坐标。对于模型2，根据这2个设计要求，可构造超越方程组。通过求解方程组获得2个形状因子，从而实现对潜艇外形的数学描述[4]。文献[4]证明了该超越方程组解的存在和唯一性，并提出了一种逐次逼近的求解方法。

对于2个以上的形状因子，不能构成适定的方程组。本文提出一种优化模型，确定Jackson船型的数学描述。以模型3-2为例，即设α4=2，设计变量取为3个（分别为艇首形状外因子α1、艇首形状内因子α2和艇尾形状外因子α3）。优化问题的数学模型可描述为

式(16)中：∇0为排水体积设计初值；xc0为浮心纵坐标设计初值；ak和bk分别为设计变量的上下界，由设计要求确定，k=1,2,3。取α1=、α2=2和α3=作为优化的初值。

采用不同的模型可构造不同的优化问题进行求解。

3 实例和数量形状因子对船体的影响

选取计算模型为美国DARPA潜艇技术规划办公室（Submarine Technology Program Office, SUBOFF）潜艇模型。SUBOFF潜艇是美国David Taylor海军舰船研究发展中心（DTNSRDC）的研究项目，相关资料较系统、全面。1989年，GROVES等对SUBOFF系列潜艇的数学模型进行了系统的论述。1990年，RODDY对SUBOFF系列潜艇进行了拘束模试验。1998年，LIU等对SUBOFF系列潜艇进行了模型试验。SUBOFF潜艇是回转体水池试验模型，其参数见表1。

表1 SUBOFF潜艇参数

利用模型 2计算得到α1=0.4和α3=1.3。因此，α1=0.4、α2=2、α3=1.3和α4=2是一组可行的形状因子，可作为优化计算的变量初值。5种模型对船体的影响比较见表2。

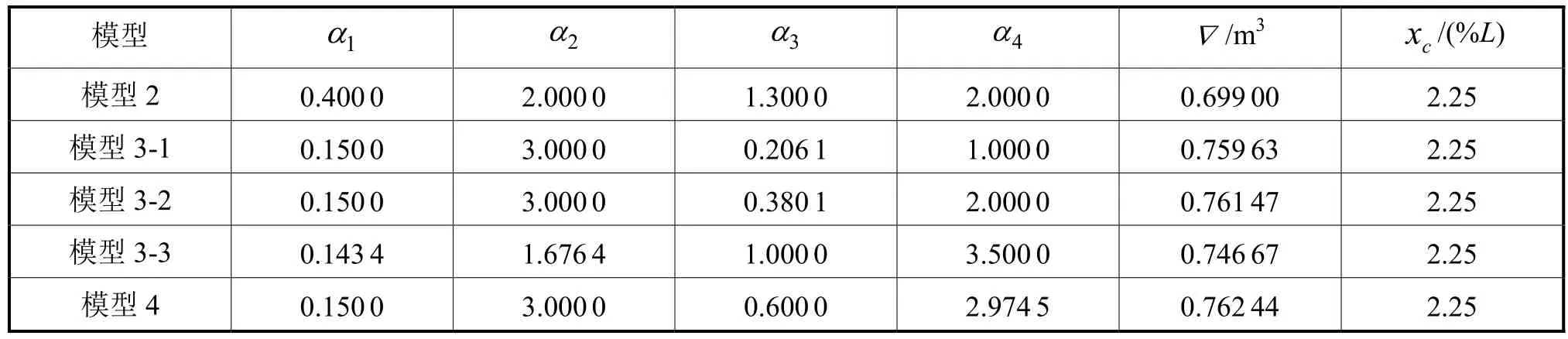
表2 5种模型对船体的影响比较

从表2中可看出，5种Jackson模型均可获得完全满足静水性条件的潜艇外形数学船型，其中2个形状因子的模型最能体现设计要求，其他模型亦可用于多学科设计优化。

4 结 语

Jackson线型控制方程广泛用于潜艇、鱼雷和导弹等具有水动力特性的物体外形描述。本文详细分析了Jackson线型控制方程的集中表现形式，指出2个形状因子的模型可利用排水体积和浮心纵坐标联立方程组获得适定解，其他形式可利用优化模型获得形状因子。实例说明了该方法的可行性。