基于数学模型素养的教学设计与反思

王慧蓉 王聪

【摘 要】本文以人教B版高中数学必修四为起点，结合课标，通过对教学内容、学习者、教学目标的分析，采用引导探究法、小组讨论法，按照复习回顾、讲授新知、例题讲解、巩固练习、课堂小结、教学反思六个环节，基于数学模型素养就《正、余弦定理应用》第一课时做了全面的教学设计与反思。

【关键词】正余弦定理;距离测量;数学模型

正、余弦定理是求解生产生活中实际问题的重要工具。通过学习正、余弦定理的应用，可以培养学生的数学模型素养以及提出问题、分析问题、解决问题和实践操作的能力[1]。笔者在教育硕士专业课《中学数学教学设计》上开展模拟授课，在合作中完成实践教学，收到了预期的教学效果。

1   课程标准要求

《普通高中数学课程标准》对本课时的要求是能用正、余弦定理解决实际的距离测量问题。

2   教学内容分析

2.1  教学内容的地位与作用

“解三角形”这一章的内容，是初中“解三角形”内容的延续与拓展。本章主要揭示三角形边角之间的数量关系，并综合利用正、余弦定理解决实际问题。

本课是人教B版必修4第九章9.2第一课时的内容，主要涉及测量距离的问题。本课时是在教学正、余弦定理之后的实际应用，因此本节课的教学内容具有理论联系实际的作用。

2.2  教材编写意图

以故宫角楼的高度测量为背景提出实际问题，引入本小节的学习内容，教师引导学生探究此问题，并让学生给出方案、解决问题的方法。设置1道例题和1道练习题。例题讲解采用交流研讨的方式，有利于展现学生的思维，让学生得出最优的解决方法，强化建立数学模型的意识，突破本节课的难点。在讲解例题后，学生已掌握解三角形实际问题的思路。接着让学生独立思考并完成练习题，巩固新知，从而使学生突破本节课的重点。最后，从解题思路进行小结，并结合思维导图加深学生的理解。

3   学习者分析

3.1  知识基础

学生已学习了三角形的有关知识和正、余弦定理，能够运用定理解决简单的问题。

3.2  数学思维

高一学生处于形式运算思维向抽象思维过渡的阶段，思维水平正逐渐提高，但空间想象能力尚有待提高。

3.3  情感态度

学生积极参与探讨测量方案（测量不可达两点的距离），合作交流，并提出质疑，进行反思。

3.4  学习困难

在求解不可达两点之间的距离问题时，学生暂时不能独立想到将不可达两点转化为可达到两点的模型，即不能独立地将空间几何问题转化为平面几何问题。

4   教学目标与重难点分析

4.1  教学目标

根据上述课程标准、教学内容分析，结合学生已有的认知结构和心理特征，制定以下教学目标。

4.1.1  情境与问题

从测量故宫角楼的高度问题出发，建立适当的数学模型，发现正、余弦定理的实际应用背景，并探讨其应用价值。

4.1.2  知识与技能

让学生能够运用正、余弦定理等解有关三角形的问题，将不可达两点间的距离测量问题转化为解三角形的问题。

4.1.3  思维与表达

通过解三角形的实际问题，培养学生提出问题、分析问题和解决问题的能力。

4.1.4  交流与反思

让学生积极主动地进行交流研讨，应用正、余弦定理解决实际问题，并从中歸纳出解决此类问题的步骤。

4.2  教学重难点

4.2.1  重点

分析测量问题的实际背景，找到测量距离的方法，运用正、余弦定理解决实际问题。

4.2.2  难点

根据实际问题建立数学模型，将实际问题抽象成一个或几个三角形，逐个解三角形，得到实际问题的解。

5   教学方法

根据教学重难点分析，教师需要在探究过程中多次引导学生将实际问题转化为数学模型，因此将第一种教学法设置为引导探究法[2]。

6   教学过程

6.1  复习回顾

教学内容：由郑和七次下西洋、徐霞客游历名山大川对我国航海和地理测量做出的突出贡献引出“解三角形”的理论在实际生活的应用，并复习正、余弦定理。

教师活动：教师拓展与实际相关的知识，回顾正、余弦定理，考查学生的掌握情况。

学生活动：回忆正、余弦定理以及公式的变形。

设计意图：通过拓展历史知识，让学生体会解三角形在生活中的广泛应用。通过复习正、余弦定理并举出生活实例，顺理成章地引出新课题。

教学反思：可以通过观看几个历史名人图片激起学生上课的积极性。

6.2  讲授新知

教学内容：在护城河对面测量故宫角楼的高度。因顶端和底部都不便到达，所以不能直接测量。引导学生思考用米尺和测量角度的工具。

Q1：你能在故宫角楼对面的岸边得出角楼的高度吗？如果能，写出你的方案，并给出有关的计算方法;如果不能，说明理由。

Q2：角楼的高度可不可以转化为不可达两点之间的距离？

教师活动：教师要多次引导，一是引导学生理解题意，把实际图形转化为数学模型，分清已知与未知，画出示意图;二是引导学生将空间图形转化为平面图形再求解;三是引导学生将已知条件与求解目标集中在一个三角形上，最后利用正、余弦定理求解。

学生活动：设计测量方案，提出解决实际问题的方法。

设计意图：由于学生的抽象能力有限，针对不可达两点问题，学生独自解题有一定的困难，所以教师要多次强调求解问题，突出教学重点，从而培养学生利用数学模型解题的素养。

教学反思：这道题属于中等难度，学生能想到利用正、余弦定理解决问题，但是在将此问题抽象成数学模型时，学生会遇到困难。因为学生掌握知识都是循序渐进的，所以可先抛出情境问题，将其放在例题后解决，更有助于培养学生解决问题的能力。

6.3  例题讲解

教学内容：A、B是某沼泽地上不便到达的两点，C、D是可到达的两点。已知A、B、C、D4点都在水面上，而且已经测得∠ACB=45°，∠BCD=30°，∠CDA=45°，∠BDA=15°，CD=100m，求AB的长。

教师活动：组织学生交流研讨，归纳学生的解题方法。

学生活动：小组讨论并提出解决此问题的方法。

设计意图：教师启发学生在解三角形时，灵活选择两个定理，寻找多种解决问题的方法。组织学生展现思维，强化学生的数学模型意识，同时突破教学难点。

教学反思：这是道典型的求解不可到达两点之间的距离的问题，因是线上授课，没有黑板，所以效果不是很好。面授时要是能在黑板上清晰地写出解题过程，效果肯定会更好。

6.4  巩固练习

教学内容：公路AB一侧有块空地OAB，其中OA=3km，OB=km，∠AOB=90°。当地政府拟在中间挖一个人工湖OMN，M、N都在边AB上（M、N不与A、B重合，M在A、N之间），且∠MON=30°，若M在距离A点2km处，求点M、N之间的距离。

教师活动：组织学生练习。

学生活动：独立思考，构建模型，解决问题。

设计意图：让学生能够完成与例题相关的练习，起过渡作用。

教学反思：练习题有点难度，部分学生无法独立解决。

6.5  课堂小结、布置作业

教学内容：

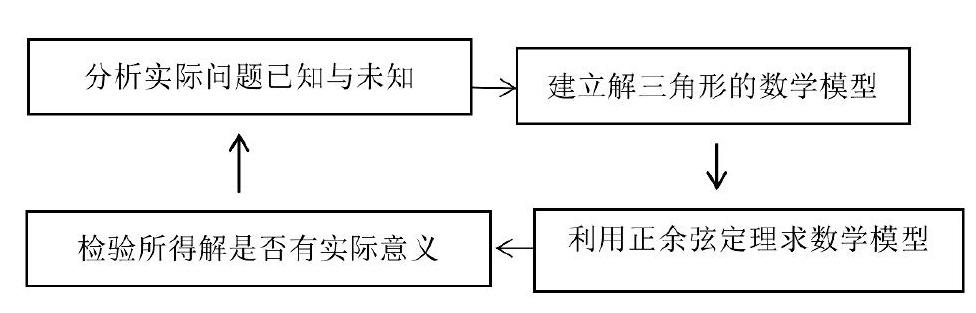
（1）解三角形的步骤，如下图。

（2）给学生预留作业，必做题为习题9-2A的第3、4题，复习题B组的第7题 ;选做题为复习题C组的第1题。

教师活动：对解题思路进行小结，由教师随机提问，并对学生的阐述归纳总结。

學生活动：依据所学新知进行总结汇报。

设计意图：紧扣教学目标，师生共同梳理解题思路，呈现出解三角形的步骤，使学生解题时得心应手。

教学反思：教师总结迅速，没有给学生回顾例题和练习题解题思路的时间。若给学生几分钟的时间理清解题思路和过程，效果会更佳。

7   教学反思总结

此教学设计的创新点是结合生活实际问题，引入情境以及利用思维导图进行总结，清晰明了，利于学生掌握。优点是教学目标定位恰当，结合了课程标准，对教材进行了深入钻研，围绕知识与技能等，制定了核心目标。同时，还能让学生在学习解三角形的实际应用中认识到数形结合的作用。

【参考文献】

[1]董强.《正余弦定理的应用（一）——距离测量问题》教学设计[J].中小学教学研究，2015（12）.

[2]管军.“解三角形的应用”教学设计与反思[J].中学数学月刊，2016（2）.

【作者简介】

王慧蓉（1995～），女，汉族，安徽安庆人，辽宁师范大学数学学院2019级在读研究生。研究方向：学科教学（数学）。

王聪（1997～），女，汉族，辽宁瓦房店人，辽宁师范大学数学学院2019级在读研究生。研究方向：学科教学（数学）。