王家坝以上流域降水量与年最大洪峰流量响应关系研究

一、引言

淮河流域地处我国南北气候过渡带，是我国旱涝频繁发生的地区，也是气候变化响应明显的地区。高超等研究表明20世纪60～80年代淮河流域年平均气温呈下降趋势，进入90年代开始显著上升。在此背景下，国内一些学者开展了相关的研究，杨赤等研究表明影响淮河上游水文极值的大气环流因子主要有西太平洋副热带高压、北半球极涡和亚洲经向环流；邓鹏等对淮河流域近50年年降水量变化研究表明年降水量呈增加趋势，存在2～3年主周期震荡和7年左右的次周期，具有南部多于北部、山区多于平原、近海多于内陆的特点；董全等研究表明流域月降水量和月平均流量存在很好的对应关系，但是比较极端的流量和降水事件线性关系不成立。洪涝灾害一般与地区的极端降水有关，在气候变化的条件下，淮河流域的重要控制站年最大洪峰流量变化也表现出一定的响应关系与周期变化规律，目前鲜有降水量与年最大洪峰流量的响应关系及年最大洪峰流量的变化规律方面的研究。淮河流域王家坝站是淮河水系的重要控制站，对流域的防汛有着重要的意义，笔者试图通过分析降水量与年最大洪峰流量的响应关系及年最大洪峰流量的变化规律，以期为流域洪水的中长期预报及水资源利用等提供参考。

二、研究区域及数据来源

淮河流域地跨鄂、豫、皖、苏、鲁五省，流域面积27万km2。王家坝站系淮河上游总控制站，集水面积30630km2，淮河上游年平均降水量为1000mm，且年际变化大，时空分布不均匀，年降水量的60%集中在5～8月，以6月、7月暴雨次数较多。根据淮河流域水资源分区，王家坝站降水量数据是王家坝以上北岸区与南岸区的平均值，王家坝站年最大洪峰量为王家坝站、钐岗站、王家坝闸、地理城四站之和。所有资料均选取1953～2012年的时间系列，为了保证数据的真实性与准确性，在计算之前对数据的可靠性、一致性进行了检验与审查。

三、降水量与年最大洪峰流量响应关系

根据王家坝站1953～2012年资料系列，作散点图分析散点变化趋势，分别采用线性函数（y=kx+b）、指数函数（y=beax）、幂函数（y=kxa）拟合降水量与年最大洪峰流量（其中用汛期降水量和年降水量分别与年最大洪峰流量拟合），分别得到汛期降水量与年最大洪峰流量的函数关系式、年降水量与年最大洪峰流量的函数关系式，见表1。其中，由于王家坝站1968年出现了异于常年的年最大洪峰流量（17600m3/s），通过对比分析研究，不包含1968年的时间系列拟合出的降水量与年最大洪峰流量的相关性得到显著性提高，故表1拟合出的函数关系式不包含1968年这个特殊年份。汛期函数关系式汛期降水量为自变量，年最大洪峰流量为因变量；全年函数关系式年降水量为自变量，年最大洪峰流量为因变量。

从表1可以看出，对于汛期函数关系式，线性函数、指数函数、幂函数拟合的函数关系式相关系数分别为0.672、0.6885、0.7328，对于全年函数关系式，线性函数、指数函数、幂函数拟合的函数关系式相关系数分别为0.6979、0.7241、0.7593，无论是汛期函数关系式还是全年函数关系式，幂函数的相关系数最大，其次是指数函数、线性函数，说明幂函数较线性函数和指数函数拟合效果好，幂函数汛期函数关系式和全年函数关系式相关系数分别达到了0.7328、0.7593，相关系数较大，这也说明了近60a 以来王家坝站以上流域降水量与年最大洪峰流量呈现较好的非线性关系，从图1也可以较为直观的看出。对于线性函数、指数函数、幂函数，全年函数关系式的相关系数均大于汛期函数关系式的相关系数，这进一步说明年降水量与年最大洪峰的相关关系比汛期降水量与年最大洪峰的相关关系好。

表1 王家坝站以上流域降水量与年最大洪峰流量的函数关系式表

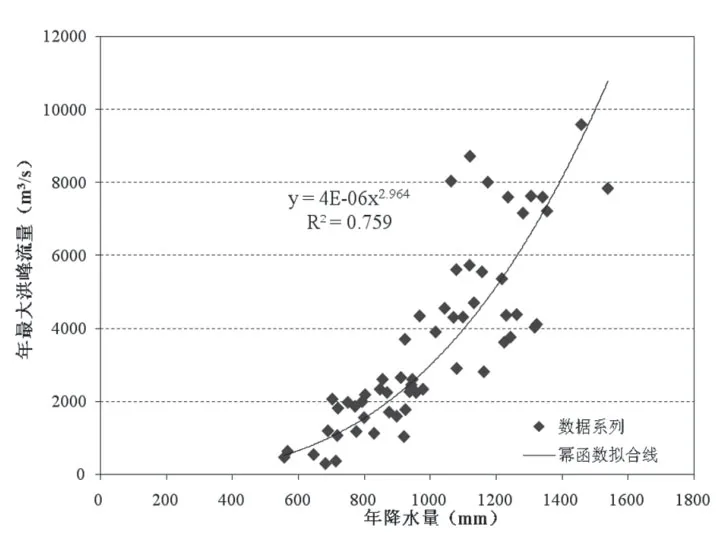
图1 王家坝站以上流域年降水量与年最大洪峰流量关系图

从图1可以看出，年最大洪峰6000m3/s以下的点据紧密分布在幂函数拟合线两边，而年最大洪峰大于6000m3/s的点据分布相对散乱。王家坝站以上流域多年平均降水量为1000mm，由拟合的关系线可知王家坝站可能出现的年最大洪峰流量为3134m3/s，根据王家坝站的水位流量关系线可知，此时对应的水位一般为27.6m，刚刚超过警戒水位27.5m。当王家坝站达到保证水位29.3m时，此时对应的洪峰流量一般为6500 m3/s，由拟合的关系线可知年降水量大约为1279mm。通过分析近年发生大洪水年份的年降水量，1991年、2003年、2007年全年的降水量分别为1236mm、1341mm、1174mm，这些年份全年降水量都非常接近1279mm，这进一步说明了年最大洪峰流量与年降水量与有着较好的响应关系，这对于流域洪水的中长期预报具有一定的指导意义。

四、年降水量与年最大洪峰流量周期变化关系

水文系统变化并不存在真正意义上的周期性，而是时而以这种周期变化，时而以另一种周期变化，并且在同一时段中又包含各种时间尺度的周期变化，即系统变化在时域中存在多层次时间尺度结构和局部化特征。基于小波分析理论，运用小波分析的多分辨率功能，对王家坝站以上流域的年降水量、年最大洪峰流量进行分析，了解其各自在不同尺度上的变化特征及是否具有相关关系。

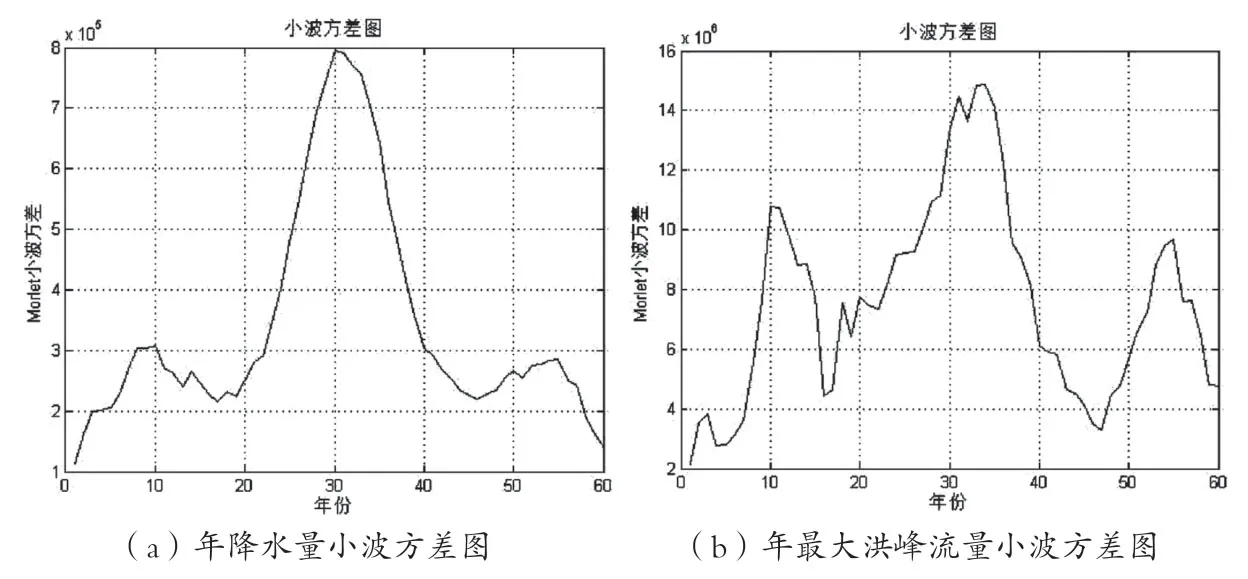
图2 王家坝站以上流域年降水量与年最大洪峰流量小波方差图

图3 王家坝站以上流域年降水量与年最大洪峰流量时频分布图

从图2（a）、（b）可知，小波方差图反映出王家坝站以上流域年降水量、年最大洪峰流量都有3个比较明显的周期变化，年降水量的3个周期分别为31年、10年、55年，最明显的周期变化为31年，年最大洪峰流量的3个周期分别为33年、11年、54年，最明显的周期变化为33年，从中不难看出，王家坝站以上流域年降水量和年最大洪峰流量最明显的周期变化均在30年左右，其次是10年左右的周期变化，55年的周期变化由于资料系列长度的问题有待进一步研究。从前面的研究可知，年最大洪峰流量与年降水量与有较好的响应关系，周期变化规律的相似性进一步说明两者呈现较好的相关关系。

图3（a）、（b）时频分布图清晰的显示了年降水量和年最大洪峰流量时间尺度变化、突变点分布及位相结构，从中可以看出不同时段各时间尺度的强弱分布。从年降水量的时频分布图可知，27～36年周期表现十分明显，中心时间尺度为31年，年降水量呈现较为显著的偏多偏少偏多交替变化规律。从年最大洪峰流量的时频分布图可知，29～37年周期表现十分明显，中心时间尺度为33年，年最大洪峰流量呈现较为显著的偏大偏小偏大交替变化规律，其次8～14年周期表现较为明显，中心时间尺度为11年，年最大洪峰流量也表现出偏大偏小偏大交替变化规律，目前正处于年最大洪峰流量偏小的周期之内。

五、结语

利用数学趋势分析模型，研究了王家坝站以上流域年降水量和汛期降水量与年最大洪峰流量的响应关系，基于小波分析理论，明晰了王家坝站以上流域年降水量、年最大洪峰流量周期变化规律及相关关系，取得了以下初步认识：

（1）王家坝站以上流域年降水量与年最大洪峰流量呈现较好的非线性关系，幂函数拟合的关系式相关系数R2到达0.7593。由拟合的关系式可知，当王家坝站以上流域年降水量大约为1000mm时，王家坝可能出现超警戒水位左右的洪峰流量。

（2）王家坝站以上流域年降水量和年最大洪峰流量最明显的周期变化均在30年左右，其次是10年左右的周期变化，年降水量和年最大洪峰流量周期变化规律呈现较好的一致性。

（3）王家坝站年最大洪峰流量表现出偏大偏小偏大交替变化的规律，目前正处于年最大洪峰流量偏小的周期之内。

由于年降水量只能反映全年大体的气候条件，降水量充沛的年份发生大洪水的可能性更大，本文只是从宏观和水文长系列方面展开了研究，以期为流域的中长期预报提供一种新的思路。但对于一次极端降水事件来说，土壤前期影响雨量、降雨时空分布、降雨历时等因素都对洪峰流量产生影响，还有待从微观方面进一步研究降雨与产流的响应机制■