基于AHP-GRA新建隧道爆破对邻近铁路隧道振动影响研究

吴波，兰扬斌，杨建新，韩亚龙

基于AHP-GRA新建隧道爆破对邻近铁路隧道振动影响研究

吴波1, 2，兰扬斌1, 2，杨建新3，韩亚龙3

(1. 广西大学 土木建筑工程学院，广西 南宁 530004；2. 广西大学 工程防灾与结构安全教育部重点实验室，广西 南宁 530004；3. 中铁十局集团第五工程有限公司，江苏 苏州 215011)

以金台铁路新建林家岙隧道为工程背景，为了科学、合理地控制新建隧道爆破施工对邻近运营铁路隧道的振动影响，采用AHP-GRA法对邻近运营隧道振动影响因素进行分析。将新建隧道爆破循环进尺的爆心距、总装药量、最大段药量和爆破循环进尺作为研究的相关因素变量，选取运营隧道迎爆侧测点振动速度、振动持续时间和振动主频作为系统的评价指标，结合现场实测数据，进行关联度计算并排序，得到邻近运营隧道综合振动影响因素的主次顺序，以及各评价指标与相关因素变量之间的关联度大小排序，其中最大段装药量和总药量对运营隧道总体振动影响最大；影响运营隧道振动主频的主要因素是最大段装药量和爆心距。AHP-GRA法的分析结果可为确定运营隧道振动影响因素的主次顺序提供科学的理论依据。

AHP-GRA；运营隧道；爆破振动；影响因素；主次顺序

随着我国国民经济的快速增长，我国铁路建设进入了高速发展的时期，无论是铁路隧道、公路隧道、还是城市轨道交通隧道，都在进行大规模的建设，由于线路的需要，会存在有些新建隧道邻近既有运营隧道进行建设，特别是山岭隧道复线修建的现象。其中比较典型的复线隧道有：成昆铁路复线隧道、渝怀铁路复线隧道、乌鞘岭复线铁路隧道等。因此，邻近既有线运营隧道进行隧道建设时，要想合理控制既有隧道的安全运营，就需要对影响运营隧道安全稳定的因素进行分析。然后根据分析结果对施工方案进行优化处理。目前，国内外应用于评价、预测隧道工程安全稳定的理论分析模型主要有人工神经网络法(ANN：artificial neural network)、回归分析法、层次分析法(AHP：analytic hierarchy process)、灰色关联度法(GRA：grey relational analysis)和模糊图法(FCM：fuzzy cognitive map。张平平等[1]通过ANN法对盾构管片接头的受力特性、管片接头的破坏类型以及管片内力和其影响因素进行敏感性分析，并比较了影响因素之间重要性。陈永雄等[2]通过组合优选的回归预测模型和模糊自适应变权重，建立了“智能监测−模型优化−信息反馈”系统，并说明该系统可以克服常规预测模型的不足。Koopialipoor等[3]通过ANN法和混合遗传算法2种智能系统对隧道钻爆作业进行预测和控制。毛正君等[4]通过AHP法建立隧道突涌水层次结构模型，对云山隧道突涌水风险等级进行了划分。Hyun等[5]通过AHP法对盾构掘进机在掘进过程中发生不良事件的潜在风险进行了研究。Nezarat等[6]通过FAHP法对隧道机械化掘进的地质风险进行排序，并指出隧道掌子面隧道失稳的概率最高。Bakhtavar等[7]通过确定隧道爆破34个影响因素，并基于FCM法来确定各爆破因素之间的交互作用。AHP-GRA法是一种对各影响因素的作用程度进行整体和局部量化排序的有效工具，该方法克服了其他方法需要收集大量的数据样本的不足，并无需考虑典型分布函数的规律，同时也弥补了GRA法分析问题的局限性。从系统工程的角度分析，爆破振动效应实际是部分未知信息和部分已知信息相结合的灰色系统[8]。本文采用AHP-GRA法评价新建隧道爆破施工对邻近运营铁路隧道振动影响，首先通过GRA法分别确定爆破参数与各个评价指标之间的灰色关联度并进行主次排序，然后结合AHP法计算爆破参数对运营铁路隧道振动的整体关联度大小并排序。最后对爆破参数进行合理、科学的调整，从而保障邻近铁路的安全运营。

1 AHP-GRA基本原理

GRA法的基本原理是通过对统计序列几何关系的比较来计算系统中多因素间的关联程度，序列曲线的几何形状越接近，则关联度越大[9]。对于传统GRA法存在一些不足的地方：1) 对各指标采用平均处理，无法反映各指标的重要性差异；2) 不同关联系数之间差异过大，使分析结果出现偏差； 3) 固定分辨系数可能会导致结果趋于平均化，人为主观因素较强[10]。AHP-GRA法是通过将专家知识和长期运行经验进行量化后赋权给各个指标，给客观评价提供了主观经验的参考，并结合动态分辨系数调整策略，有效的弥补了传统GRA法的不足。

1.1 AHP法确定权重

1.1.1 建立层次模型

AHP法解决实际问题一般分为3个层级[11]，分别为目标层(最终需选取的方案)、准则层(各评价指标，可能有多层)和方案层，相邻层级间的因素会相互影响。

1.1.2 构建判断矩阵

本文采用九标度法[12]构建判断矩阵=(a)×，其中a为准则层内指标A相对于A的重要程度，具体判断尺度量化规则见表1。

表1 判断尺度量化规则

1.1.3 计算指标权重

1.1.4 一致性检验

求解判断矩阵的最大特征值max及其所对应的特征向量，并计算值，若＜0.1，即可认为判断矩阵满足一致性要求。则可确定为该层指标相对于上一层目标层(或上一次指标层)的权重向量。式(2)为值的计算公式。

式中：为准则层内指标个数；为平均随机一致性指标，具体取值规则见表2。

表2 RI取值表

1.2 GRA法操作步骤

1.2.1 确立母、子序列

母序列对应系统特征变量，即评价指标；子序列对应相关因素变量。

系统特征变量为：

相关因素向量为：

1.2.2 无量纲处理

由于系统中不同的特征变量和相关变量所表示的含义差异性均较大，因此需要对特征变量和相关变量中的数据进行无量纲处理，也即归一化处理，将其线性映射到[0,1]区间内，如式(5)~(6)所示。

1.2.3 确定关联系数

1.3 计算关联度

1.3.1 调整分辨系数

根据式(6)发现分辨系数会对关联系数值产生直接影响，为了克服人为设定值带来的不足，本文采用一种分辨系数调整策略[10]，使得模型评价结果更加客观可信。定义分辨系数分解判断因子为：

当=0时，在区间[0,1]内任意取值；当0＜＜0.5时，表示数据不稳定，指标可能会出现异常值，此时取=4；当＞0.5，表示数据较稳定，此时在区间[0.8,1]中任意取值。最终确定关联系数矩阵为：

1.3.2 计算整体关联度

结合式(1)和式(8)，可以得到评价模型的整体关联度矩阵为：

2 工程案例分析

2.1 工程概况

金台铁路林家岙隧道穿行于丘陵区，全长4 933 m，起讫里程为LDgK3+721~LDgK8+654。隧道所处地形起伏大，海拔高程15~486 m，相对高差120~470 m，自然坡度15°~35°，隧道最大埋深约462m。本隧道与邻近线杭深铁路黄毛山隧道并行，与营业线间距为35~300 m，其中隧道进口与既有营业线间距为35 m，出口与既有营业线间距为36.5 m，对应既有营业线里程为K470+063~K474+996。图1为新建隧道与邻近隧道的位置关系。

2.2 测试方案

现场总共进行了53次测试，测试地点选在林家岙隧道进口处，如图2所示，左边为林家岙隧道进口，右边为杭深铁路黄毛山隧道进口。此次主要是对新建隧道里程段为LDgK3+721~LDgK3+805爆破所产生的振动影响进行分析，该里程段内围岩较为破碎，为Ⅴ级围岩，爆破开挖方式选用短台阶爆破开挖，掏槽形式为常规楔形掏槽，周边眼采用预裂爆破，炮孔直径为42 mm；邻近运营铁路隧道振速测试里程段为K470+063~K470+147，测点布置在运营隧道迎爆侧拱腰和拱脚处，并且随着新建隧道掌子面的推进而移动，具体测点布置如图3所示。现场第1次爆破测试为上台阶爆破，所采用的具体爆破参数见表3。

图1 新建隧道与运营隧道位置关系

图2 隧道进口

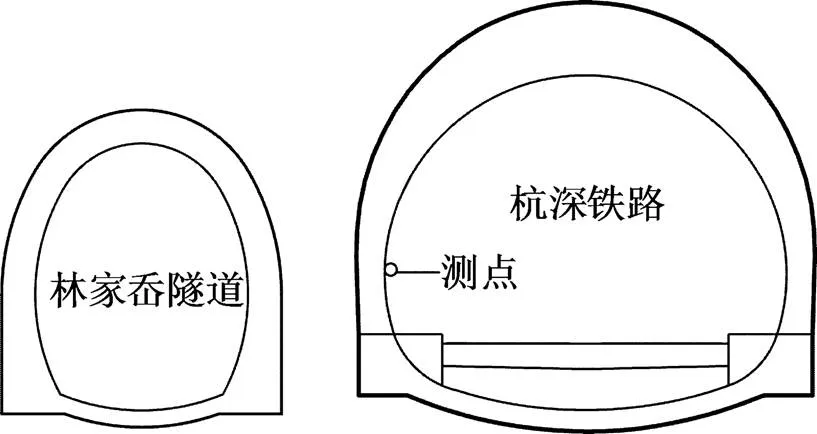
图3 测点布置图

表3 上台阶爆破参数表

现场爆破施工所采用的雷管段别均为8段，且每段所对应的延时时间都是固定的。监测设备采用成都中科测控公司的TC−4850新型测振仪，该仪器可精确地记录振动时间、振动数值等相关参数，仪器携带、操作方便。本次在现场共测试了53次，选取其中12组实测数据作为灰色关联度分析的样本值。图4为TC−4850测振仪。

图4 TC−4850测振仪

2.3 AHP-GRA模型建立

由文献[13−15]可知，评价爆破振动危害程度的主要指标有振动速度、持续时间和主频。因此本文将这3个因素作为系统指标层的特征变量，可记为Y(=1,2,3)，其中：1表示测点最大振速峰值，2表示振动波持续时间，3表示爆破振动的主频。

表4 现场实测数据样本值

在新建隧道爆破施工过程中，对邻近运营隧道产生爆破振动的主要因素有爆心距、总药量、爆破循环进尺、最大段装药量、围岩条件和装药结构等。由地勘资料可知现场测试段隧道的围岩等级均为Ⅴ级，所采用的雷管段别均为8段，且每段所对应的延时时间都是相同的，因此没有考虑爆破延时和药量拆分的影响。结合现场情况综合考虑，本文选取爆心距、总药量、爆破循环进尺、最大段装药量作为相关因素变量，可记为X(=1,2,3,4)。在运营隧道迎爆侧拱腰处布置测点，测点与新建隧道掌子面始终保持在同一平面上。表4为现场测试后整理的采集数据。

3 灰色关联度计算与分析

3.1 灰色关联度计算

3.1.1 计算指标权重矩阵

参照表5可计算指标权重值。

表5 判断矩阵和权重

1) 将矩阵每一列正规化处理得到判断矩阵为：

2) 将判断矩阵按行相加得：

(1,2,3)=(1.28,0.44,1.28)

3) 将向量(1.28,0.44,1.28)T正规化得Σ=3，则所求特征向量=(0.43,0.14,0.43)T。

4) 计算判断矩阵最大特征值max：

即max=Σ[()/]=3.032；=(max−)/(−1)= 0.016；/=0.016/0.58= 0.027＜0.1达到一致性要求。

3.1.2 计算灰色关联矩阵

1) 由于3个评价指标都是越小越优，因此选择逆向指标，将相关因素和特征变量归一化得到整理后数据见表6。

2) 根据式(7)计算得分辨系数分界判断因子均大于0.5，取=0.9。

3) 将=0.9和表5中得数据代入式(6)中，计算得灰色关联度见表7。

4) 采用平均值处理每个相关因素变量相对于评价指标的灰色关联度，得到灰色关联矩阵为：

3.1.3 计算整体关联度

将灰色关联矩阵和指标权重矩阵相乘得最终的整体关联度=[0.733 0.763 0.711 0.790]T。

表6 归一化数据

表7 灰色关联度计算值

3.2 灰色关联度结果分析

根据计算得到新建隧道对邻近运营隧道爆破振动影响的灰色关联度结果如图5所示。

图5 影响因素排序

1) 根据AHP-GRA计算所得的整体关联度可知，在爆心距、总装药量、爆破循环进尺和最大段装药量因素中，最大段装药量对运营隧道的振速、持续时间和主频的综合影响最大，其次是总装药量和爆心距。

2) 各相关因素对邻近运营隧道振动速度的影响从大到小依次是最大段装药量、总装药量、爆心距、爆破循环进尺，其中最大段装药量和总装药量起主要作用。

3) 各相关因素对邻近运营隧道振动持续时间的影响从大到小依次是最大段装药量、总装药量、爆破循环进尺、爆心距，其中最大段装药量和总装药量起主要作用。

4) 各相关因素对邻近运营隧道振动主频的影响从大到小依次是最大段装药量、爆心距、总装药量、爆破循环进尺，其中最大段装药量和爆心距起主要作用。

4 结论

1) 通过AHP-GRA法，确定新建隧道采用4种不同爆破参数下对邻近运营隧道爆破振动的综合影响的主次关系，为邻近运营隧道进行爆破施工采取合理的爆破参数和控制措施提供参考。另外，AHP-GRA法所需的样本容量较小，并能得到良好的效果，建议在今后类似的工程安全评估中推广应用。

2) 新建隧道爆破施工对邻近运营隧道振动影响相对较大的因素是最大段装药量，在最大段装药量固定的条件下，主要受总装药量的影响。因此，为了有效地降低新建隧道爆破施工对邻近运营隧道的振动影响，应降低最大段装药量，同时减小爆破循环进尺。

3) 最大段装药量和爆心距对运营铁路隧道振动主频的影响相对较大，当振动频率与行进列车的频率接近时将对列车行车安全造成极大的威胁，因此，在运营隧道附近进行爆破作业时主要关注最大段装药量和爆心距。

4) 采用AHP-GRA法既可以整体分析影响运营隧道振动破坏的主次因素，又能得出每个评价指标所对应相关因素的具体关联度大小排序，这对于合理有效地控制爆破施工对邻近运营隧道的振动破坏具有极大的意义。

[1] 张平平, 杨伟超, 尹荣申, 等. 盾构管片接头破坏类型及参数敏感性分析[J]. 铁道科学与工程学报, 2019, 16(2): 450−456. ZHANG Pingping, YANG Weichao, YIN Rongshen, et al. Failure type and parameter sensitivity analysis of shield segment joint[J]. Journal of Railway Science and Engineering, 2019, 16(2): 450−456.

[2] 陈永雄, 吴小萍, 郜成成, 等. 隧道围岩变形预测模型的优化与应用[J]. 铁道科学与工程学报, 2019, 16(2): 426−434. CHEN Yongxiong, WU Xiaoping, GAO Chengcheng, et al. Optimization and application of prediction method of tunnel surrounding rock deformation[J]. Journal of Railway Science and Engineering, 2019, 16(2): 426− 434.

[3] Koopialipoor M, Jahed Armaghani D, Haghighi M, et al. A neuro-genetic predictive model to approximate overbreak induced by drilling and blasting operation in tunnels[J]. Bulletin of Engineering Geology and the Environment, 2019, 78(2): 981−990.

[4] 毛正君, 杨绍战, 朱艳艳, 等. 基于F-AHP法的隧道突涌水风险等级评价[J]. 铁道科学与工程学报, 2017, 14(6): 1332−1339. MAO Zhengjun, YANG Shaozhan, ZHU Yanyan, et al. Risk grade evaluation of tunnel water inrush based on fuzzy analytic hierarchy process[J]. Journal of Railway Science and Engineering, 2017, 14(6): 1332−1339.

[5] Hyun K, Min S, Choi H, et al. Risk analysis using fault-tree analysis (FTA) and analytic hierarchy process (AHP) applicable to shield TBM tunnels[J]. Tunnelling and Underground Space Technology, 2015, 49(6): 121− 129.

[6] Nezarat H, Sereshki F, Ataei M. Ranking of geological risks in mechanized tunneling by using fuzzy analytical hierarchy process (FAHP)[J]. Tunnelling and Underground Space Technology, 2015, 50(8): 358−364.

[7] Bakhtavar E, Shirvand Y. Designing a fuzzy cognitive map to evaluate drilling and blasting problems of the tunneling projects in Iran[J]. Engineering with Computers. 2019, 35(1): 35−45.

[8] 李斌, 毕延华, 刘新伟. 基于灰色关联分析浅埋隧道爆破振动影响因素[J]. 工程爆破, 2018, 24(4): 86−90. LI Bin, BI Yanhua, LIU Xinwei. Influence factors of blasting vibration of shallow tunnel based on grey relational analysis[J]. Engineering Blasting, 2018, 24(4): 86−90.

[9] 施建俊, 张琪, 李庆亚, 等. 基于灰色分析和神经网络的爆破振速峰值预测[J]. 中国矿业, 2016, 25(增1): 410−415. SHI Jianjun, ZHANG Qi, LI Qingya, et al. Prediction of peak velocity of blasting vibration based on pray analysis and neural network[J]. China Mining Magazine, 2016, 25(Suppl 1): 410−415.

[10] 周依希, 李晓明, 瞿合祚, 等. 基于AHP-灰色关联度的复杂电网节点综合脆弱性评估[J]. 电力系统保护与控制, 2018, 46(23): 86−93. HOU Yixi, LI Xiaoming, QU Hezuo, et al. Node integrated vulnerability assessment of complex power grid based on AHP-gray relational degree method[J]. Power System Protection and Control, 2018, 46(23): 86− 93.

[11] 赵保卿, 李娜. 基于层次分析法的内部审计外包内容决策研究[J]. 审计与经济研究, 2013, 28(1): 37−45. ZHAO Baoqing, LI Na. Research on outsourcing content decision of internal audit based on analytic hierarchy process[J]. Journal of Audit & Economics, 2013, 28(1): 37−45.

[12] 张曾莲. 风险评估方法[M]. 北京: 机械工业出版社, 2017. ZHANG Zenglian. Risk assessment methods[M]. Beijing: China Machine Press, 2017.

[13] 范磊, 龙源, 郭涛, 等. 基于反应谱理论的爆破振动破坏评估标准分析[J]. 爆破, 2010, 27(1): 5−10. FAN Lei, LONG Yuan, GUO Tao, et al. Harm evaluation standard analysis of blasting vibration based on response spectrum theory[J]. Blasting, 2010, 27(1): 5−10.

[14] 张小军, 汪旭光, 王尹军, 等. 基于正态分布的爆破振动评价与安全药量计算[J]. 爆炸与冲击, 2018, 38(5): 1115−1120. ZHANG Xiaojun, WANG Xuguang, WANG Yinjun, et al. Blasting vibration evaluation and safe charge calculation based on normal[J]. Explosion and Shock Waves, 2018, 38(5): 1115−1120.

[15] 杜林林, 刘维宁, 刘卫丰, 等. 城市轨道交通环境振动评价指标计算与分析[J]. 都市快轨交通, 2017, 30(5): 40−45. DU Linlin, LIU Weining, LIU Weifeng, et al. Computation and analysis of evaluation indicators of environmental vibration induced by urban rail transit[J]. Urban Rapid Rail Transit, 2017, 30(5): 40−45.

Study on vibration effect of blasting of new tunnel based on AHP-GRA method on adjacent railway tunnel

WU Bo1, 2, LAN Yangbin1, 2, YANG Jianxin3, HAN Yalong3

(1. College of Civil Engineering and Architecture, Guangxi University, Nanning 530004, China; 2. The Key Laboratory of Disaster Prevention and Structural Safety of Ministry of Education, Guangxi University, Nanning 530004, China;3. China Railway l0th Bureau Group No. 5 Engineering Co., Ltd, Suzhou 215011, China)

In order to scientifically and reasonably control the vibration influence of blasting construction of newly-built tunnels on adjacent railway tunnels, this paper uses AHP-GRA method to analyze the influencing factors of vibration of adjacent railway tunnels, taking the newly-built Linjiaao Tunnel of Jintai Railway as the engineering background. The distance of blasting center, the total charge, the maximum charge and the blasting cycle feed of new tunnel blasting were taken as the relevant variables in the study. The vibration velocity, duration and main frequency of the measured points on the explosion-prone side of the operating tunnel were selected as the evaluation indexes of the system. In addition, combined with the field measured data, the correlation degree was calculated and sorted, and the primary and secondary order of the factors affecting the comprehensive vibration of adjacent operating tunnels was obtained. The order of the correlation degree between each evaluation index and relevant variables was obtained. Among them, the maximum charge and the total charge have the greatest impact on the overall vibration of the operating tunnel. The main factors affecting the main frequency of vibration in operating tunnels are the maximum charge amount and the distance between the detonation centers. The results of AHP-GRA method can provide a scientific theoretical basis for determining the order of influencing factors of vibration of operating tunnels.

AHP-GRA; operation tunnel; blasting vibration; influence factor; primary and secondary order

U455.6

A

1672 − 7029(2020)03 − 0668 − 08

10.19713/j.cnki.43−1423/u.T20190373

2019−05−05

国家自然科学基金面上资助项目(51478118，51678164)；广西特聘专家专项资金资助项目(20161103)；广西自然科学基金资助项目(2018 GXNSFDA138009)；广西科技计划项目(桂科AD18126011)；广西大学科研基金资助项目(XTZ160590)；广西岩土与地下工程创新团队资助项目(2016GXNSFGA380008)

吴波(1971−)，男，四川阆中人，教授，博士，从事隧道及地下工程方向的教学与研究工作；E−mail：813792833@qq.com

(编辑 阳丽霞)