汽车制动作用下混凝土梁桥下部结构动力响应分析

杨婷婷，李岩，李全林

汽车制动作用下混凝土梁桥下部结构动力响应分析

杨婷婷1，李岩2，李全林3

(1. 哈尔滨工业大学 土木工程学院，黑龙江 哈尔滨 150090；2. 哈尔滨工业大学 交通科学与工程学院，黑龙江 哈尔滨 150090；3. 深圳高速工程顾问有限公司，广东 深圳 518094)

将制动力系数变化拟合为时变斜坡函数，由变形协调条件和力的平衡方程推导车辆各轮时变制动力，进而建立考虑汽车制动作用的车桥耦合空间动力分析模型并编制计算程序。依托某混凝土梁桥工程实例，采用所编制的程序，分析汽车制动作用下桥梁下部结构的动力行为特性。系统开展初始车速、制动加速度上升时间、制动峰值系数和车重等关键参数对桥梁下部结构动力响应的影响分析。研究结果表明：车辆制动作用下墩顶纵桥向动力响应显著，且该响应随制动加速度上升时间的缩短、制动峰值系数及车重的提高而大幅增加，初始车速对其有影响但无单调性规律。

混凝土梁桥；车桥耦合振动；制动作用；下部结构；动力分析

现有的车桥耦合振动研究，主要考虑车辆匀速过桥状况，对于实际运营中常见的车辆制动和变速行驶等状况较少涉及。且多数研究关注车辆制动作用对桥梁上部结构竖向动力行为的影响，研究结果表明车辆制动时引起的桥梁竖向动力冲击效应较匀速作用下更为显著[1−3]。而对于车辆制动作用更为敏感的桥梁下部结构，其车辆制动作用下的动力行为研究还鲜有报道。近年来，基于动力的桥梁下部结构损伤诊断相关研究已获得广泛关注，其中基于车桥耦合振动的结构损伤识别研究也得到初步开展[4]。如Foti等[5]采用数值分析和试验方法研究基础冲刷对车辆作用下桥梁动力响应的影响，指出通过对车载作用下桥墩动力响应的比较分析进行基础冲刷识别的可行性；Prendergast等[6]通过建立车−桥−土相互作用模型分析冲刷对桥梁频率及振型的影响，研究发现桥墩局部振动对应模态对其附近的冲刷很敏感；NIE等[7]提出基于列车动力作用进行桥梁下部结构损伤诊断的理论框架，分析了列车速度、墩高及地基土种类等对桥梁动力响应的影响。显然，桥梁下部结构的水平向动力响应对车辆制动作用更为敏感，因此，将车辆制动激励作为桥梁下部结构损伤识别的激励源具有很好的应用潜力。考虑多种影响因素深入分析汽车制动作用下桥梁下部结构的动力反应特点和规律，可为后继的相关研究提供基础和参考。为此，本文依托实际桥例，建立考虑车辆制动作用的车桥耦合振动空间分析模型，系统分析初始车速、制动加速度上升时间、制动峰值系数和车重等多种关键因素对汽车制动作用下桥梁下部结构动力响应的影响规律，结果可为基于车辆制动作用的桥梁下部结构状态评估和诊断方法研究提供依据和参考。

1 车辆和桥梁分析模型

1.1 车辆分析模型

(a) 立面图；(b) 横断面图

1.2 桥梁概况与分析模型

以黑龙江宁安一座跨牡丹江的预应力混凝土梁桥为工程背景，该桥桥跨布置为16 m+4×40 m+4×40 m+2×16 m，选取中跨第2联4×40 m预应力混凝土连续梁桥为分析对象，桥宽25 m，双向4车道布置，其横断面如图2所示。主梁、桥墩、桩基分别采用C50，C30及C25混凝土；基础采用钻孔灌注桩，桩径为2.2 m，长17~19 m；桥墩为柱式墩，直径1.6 m，高5.5~8.4 m。支座采用板式橡胶支座(3号墩顶处)和聚四氟乙烯滑板橡胶支座(1号，2号，4号和5号墩顶处)2种形式。

单位：cm

采用Midas/Civil建立桥梁空间有限元模型(如图3所示)，其中主梁、墩柱和桩采用空间梁单元模拟；对聚四氟乙烯滑板橡胶支座建模时一般采用双线性模型进行模拟[9]，但由于一辆三轴车制动所产生水平荷载并未超过本桥所用型号支座的临界摩擦力，故可对其滞回特性不予考虑，因此采用三维线性弹簧模拟支座，其6个自由度方向弹性刚度如表1所示。同时，为计入相邻桥跨对研究对象的影响，模型中利用节点弹性支撑来增加边墩顺桥和横桥向平动约束；桩身纵向、横向考虑周土体对桩的弹性效应利用沿深度变化的节点弹性支撑模拟，双向土弹簧约束刚度根据“m法”计算得到。

表1 支座刚度计算结果

图3 桥梁有限元模型

2 车辆制动作用下车桥振动分析方法

2.1 车桥耦合振动分析原理

对于车辆匀速过桥情况，利用车桥接触点的位移和作用力的协调和平衡关系，可建立车桥耦合系统的整体运动方程：

式中：，和分别为质量、阻尼和刚度矩阵；v和B分别为车辆和桥梁位移响应向量；表示车桥系统的荷载向量；符号下标“B”代表桥梁；符号下标“v”代表车辆；符号下标“Bv”和“vB”表示车桥耦合项；符号上标“r”和“G”分别表示由于桥面不平度和车辆自重产生的作用力。车桥系统振动方程中的质量、刚度、阻尼和荷载向量可由车桥系统间的力和位移协调条件推导得到，文献[8]中对此具体内容进行了详细推导，此不赘述。利用通用有限元软件建立桥梁计算模型并进行模态分析，提取结构振型和频率等模态信息用于计算车桥动力响应。以下重点论述考虑车辆制动的车桥耦合振动分析模型建立方法和过程。

2.2 考虑车辆制动的车桥耦合振动分析模型

车辆制动过程中，通过轮胎与桥面间的摩擦力使车辆减速，随车速变化，摩擦力大小不断改变。定义路面制动力与垂直载荷之比为制动系数，其值不仅与路面和轮胎的材料及状态有关，还与它们之间的滑动率有关。为防止刹车时车轮抱死引起打滑，现多数车辆已设计有防抱制动装置(ABS系统)。本文研究对象为装有ABS的车辆，其制动过程可分为2个阶段[10]：1) 常规制动阶段：当滑移率在0~20%时，ABS不起作用，车轮未处于抱死滑移状态，随滑移率增加，制动系数逐渐增大；2) ABS控制阶段：随着滑移率提升，系统通过控制和不断调整制动压力，将车轮滑移率控制在最佳滑移率20%(对应制动系数峰值φ)的附近，防止车轮抱死，使每个车轮尽可能获得最大的地面制动力。

现将汽车制动过程中的制动系数假定为一个斜坡函数[11]，即制动系数从0线性地增加至峰值φ，然后保持恒定不变直至汽车在桥上停止或者驶出桥梁，可表示为：

式中：φ为制动峰值系数，其取决于轮胎和路面的种类及使用状况，另外还与轮胎的结构、气压、车速以及运动状况有一定的关系；t为制动系数的上升时间，s。

车辆制动导致的悬架变形和受力情况如图4所示。当车辆制动时，假设只存在纵向加速度[12]，可建立车体受力平衡方程：

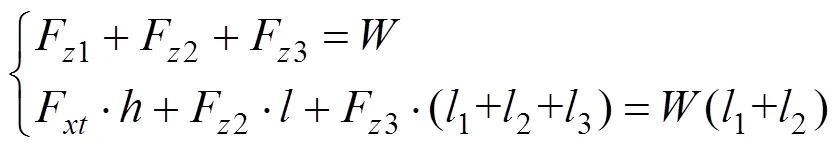
式中：Fzi为第i轴分配得地面反作用力；W为车辆总重；Fxt为地面制动力，Fxt=Wφ。

假设车辆簧载质量为刚性，各悬架位置受到刚性约束[13]。上述悬架变形可由如下几何关系描述：

联立式(2)~(4)可得到各轴车轮制动力如下：

考虑车辆制动作用影响，前述车桥耦合运动方程可改写为：

基于上述原理，笔者采用Matlab编制了相应的车桥耦合振动分析程序，并利用实桥动力试验数据对所提出的方法和程序的准确性和适用性进行了验证，结果表明该方法具有较好的精度，可用于相关问题的数值分析研究[14]，过程详见文献。

3 汽车制动作用下桥梁下部结构动力响应特征及参数分析

3.1 汽车制动作用下桥墩动力响应特征

基于所建立的制动作用下车桥振动分析方法和程序，针对前述桥例及三轴重车，考虑桥面不平度等级为“好”，汽车以初速度50 km/h由车道2驶入桥梁的工况进行桥墩动力响应特点分析。依据既有研究[15]，普通轮胎的汽车在干燥的柏油或是水泥马路上制动，制动系数峰值φ取值为0.7。制动力上升时间为0.3 s，汽车制动后前轮停止在3号墩处，得到各桥墩墩顶动力响应如图5所示。

由图5~6可见，车辆制动作用下墩顶纵向动力响应显著，竖向和横向动力响应幅值较小。汽车开始制动后0.3 s内处在减速度上升区段，纵向制动力不断增大，此时各墩顶纵向动力响应均逐渐增加；停车瞬间制动力消失，相当于车辆对桥梁突加反向荷载，此时桥梁墩顶出现制动过程的纵向振动加速度极值。此外，支座刚度差异造成不同墩顶处纵向动力响应存在较大差别，其中2号墩的动力响应最为显著。

(a) 纵桥向；(b) 横桥向；(c) 竖向

考虑汽车制动的车桥系统动力反应受多种因素影响，为解释其影响规律和机理，本文将对制动车辆的初速度、制动力上升时间、制动峰值系数和车重等关键参数对墩顶纵向动力响应的影响开展深入分析。

3.2 车辆初速度的影响

考虑制动车辆分别以30，50及70 km/h的初速度驶入桥梁，其他参数与3.1节相同，得到2-1号墩顶纵桥向动力响应如图7所示。

由图7可见，在车辆制动停车前，车辆初速度对墩顶纵向动力响应幅值影响不大；而在制动停车后墩顶纵向位移和加速度响应幅值受初始速度影响显著，但无明显线性规律。其中初始车速50 km/h对应的最大加速度响应18.56 mm/s2，较车速为30 km/h和70 km/h增加了73.61%及31.83%，而对于位移响应幅值也由50 km/h时达到最大，达到0.7 mm，相比于初始速度为30 km/h及70 km/h时的位移响应峰值分别增加了0.29 mm(68.72%)和0.04 mm (6.40%)。由此可知，制动结束后，相比于位移，墩顶纵向加速度响应对车辆制动初速度变化更 敏感。

(a) 纵桥向；(b) 横桥向；(c) 竖向

(a) 纵向加速度；(b) 纵向位移

3.3 制动加速度上升时间的影响

车辆以50 km/h初速度由车道2驶入桥梁并制动停止在3号墩处，制动峰值系数达到0.7，分别选取制动加速度上升时间为0.3，1.2，2.1和3 s 4种工况，考察制动加速度上升时间对桥梁下部结构纵向动力响应的影响。仍以2-1号桥墩顶纵向动力响应为例予以说明(如图8)。

由图8可知，制动力上升时间对墩顶纵桥向振动的影响显著，上升时间越短桥墩振动响应越大。其中制动力上升时间0.3，1.2和2.1 s对应的加速度峰值响应分别较3 s时增加了56.71%，32.27%和14.60%；对应的位移响应峰值分别增加了67.55%，12.15%和8.82%。

3.4 制动峰值系数的影响

选取制动过程制动峰值系数分别为0.3，0.5及0.7模拟不同的刹车状态，桥面平整度等级为“好”，车辆以50 km/h的初速度通过车道2驶入桥梁并制动停止在3号墩处，制动加速度上升时间均为0.3 s，对比分析2-1号桥墩墩顶纵桥向的动力响应时程，如图9所示。

可见制动峰值系数对桥墩顶纵桥向振动有显著的影响，随着制动峰值系数增加桥墩振动明显增大。其中当制动峰值系数φ=0.5以及φ=0.7时，相对φ=0.3时对应的加速度峰值和位移峰值分别增加了29.57 %和192.03 %以及68.55%和138.18 %。

(a) 纵向加速度；(b) 纵向位移

(a) 纵向加速度；(b) 纵向位移

(a) 纵向加速度；(b) 纵向位移

3.5 车重的影响

标准车重(29 802 kg)，1.2倍车重(35 762 kg)，1.5倍车重(44 703 kg)3种工况，桥面平整度等级为“好”，以初速度50 km/h单车由车道2驶入桥梁并制动停止在3号墩处，制动峰值系数达到0.7，分析车重对桥梁下部结构纵桥向动力响应的影响，以2-1号墩为例，结果见图10。可见随着车重由标准车增加到1.2倍和1.5倍车重，墩顶纵桥向加速度峰值分别增加了18.86%和49.86%，位移增加了20.15%和49.98%。表明车重对墩顶纵桥向动力响应影响明显，且随着车重增加，动力响应显著增大。

4 结论

1) 车辆制动作用下，桥墩纵桥向动力响应相对竖向和横向响应更为显著，适宜作为下部结构状态评估的动力信号源。

2) 车辆制动作用下，初始车速对墩顶纵向动力响应影响明显，但无单调性关系。

3) 制动力上升时间、制动峰值系数和车重对车辆制动作用下桥墩纵向振动响应均有明显影响，且该响应随制动上升时间的缩短、制动峰值系数和车重的增大而出现大幅增加。

[1] 殷新锋, 方志. 车辆制动作用下的车辆−路面−桥梁系统随机振动分析[J]. 计算力学学报, 2010, 27(5): 936− 41. YIN Xinfeng, FANG Zhi. Random vibration analysis of vehicle-pavement-bridge system under vehicle braking[J]. Chinese Journal of Computational Mechanics, 2010, 27(5): 936−941.

[2] 邓露, 王芳. 汽车制动作用下预应力混凝土简支梁桥的动力响应及冲击系数研究[J]. 湖南大学学报(自科版), 2015, 42(9): 52−58. DENG Lu, WANG Fang. Study of the dynamic response and impact factors of simply-supported prestressed concrete girder bridges due to vehicle braking[J]. Journal of Hunan University (Natural Sciences), 2015, 42(9): 52− 58.

[3] Hoang H P, Pham T D, Pham Q T, et al. Dynamic response of bridge-vehicle three phases interaction considering the effects of sudden heavy braking[J]. International Journal of Advanced and Applied Sciences, 2019, 6(2): 39−47.

[4] 黄进鹏, 黄杰忠, 张纯, 等. 基于车桥耦合振动信号和扩展卡尔曼滤波的桥梁结构损伤识别[J]. 土木工程与管理学报, 2018, 35(5):143−147, 154. HUANG Jinpeng, HUANG Jiezhong, ZHANG Chun, et al. Bridge damage identification based on vehicle- bridge coupling vibration signals and extended kalman filtering[J]. Journal of Civil Engineering and Management, 2018, 35(5): 143−147, 154.

[5] Foti S, Sabia D. Influence of foundation scour on the dynamic response of an existing bridge[J]. Journal of Bridge Engineering, 2011, 16(2): 295−304.

[6] Prendergast L J, Gavin K, Hester D. Isolating the location of scour-induced stiffness loss in bridges using local modal behaviour[J]. Journal of Civil Structural Health Monitoring, 2017, 7(4): 483−503.

[7] NIE Rusong, CHEN Y F, LENG Wuming, et al. Experimental measurement of dynamic load parameters for pier pile caps of high-speed railway bridges[J]. Proceedings of the Institution of Mechanical Engineers Part F Journal of Rail & Rapid Transit, 2015, 231(2): 10−12.

[8] LI Yan, CAI C S, LIU Yang, et al. Dynamic analysis of a large span specially shaped hybrid girder bridge with concrete-filled steel tube arches[J]. Engineering Structures, 2016, 106(1): 243−260.

[9] 李正英, 蒋林均, 李正良. 曲线连续梁桥支座模型对结构地震反应影响分析[J]. 振动与冲击, 2015, 34(2): 182−86. LI Zhengying, JIANG Linjun, LI Zhengliang. Effect of bearing model on the seismic response of curved continuous girder bridge[J].Journal of Vibration and Shock, 2015, 34(2):182−186.

[10] Harifi A, Aghagolzadeh A, Alizadeh G, et al. Designing a sliding mode controller for slip control of antilock brake systems[J]. Transportation Research Part C Emerging Technologies, 2008, 16(6): 731−741.

[11] 姚东强, 谭永营, 吴文文. 某型车辆防抱死控制系统设计与分析[J]. 山东工业技术, 2017(21): 24−25. YAO Dongqiang, TAN Yongying, WU Wenwen. Design and analysis of an anti-lock braking control system for a certain type of vehicle[J]. Shandong Industrial Technology, 2017(21): 24−25.

[12] 黄新艺. 混凝土连续曲线梁桥在车辆荷载作用下的动力响应研究[D]. 哈尔滨: 哈尔滨工业大学, 2008: 94−99. HANG Xinyi. Dynamic response research of continuous curved concrete bridges under moving vehicle[D]. Harbin: HarbinInstituteof Technology, 2008: 94−99.

[13] 汪知望, 钱友军, 郭春雷. 中卡三轴载货车制动系统的匹配设计[J]. 合肥工业大学学报(自然科学版), 2007, 30(增1): 22−24, 61. WANG Zhiwang, QIAN Youjun, GUO Chunlei. The match design of braking system for a triaxial mid-sized- truck[J]. Journal of Hefei University of Technology, 2007, 30(Suppl 1): 22−24, 61.

[14] 杨婷婷. 基于变速行驶车辆激励的桥梁下部结构损伤诊断方法研究[D]. 哈尔滨: 哈尔滨工业大学, 2019: 18−20. YANG Tingting. Damage detection method for substructure of bridges based on vehicle excitation with variable velocity[D]. Harbin: HarbinInstituteofTechnology, 2019: 18−20.

[15] Gillespie T D. 车辆动力学基础[M]. 北京: 清华大学出版社, 2006: 229−231. Gillespie T D. Vehicle dynamics foundational study[M]. Beijing: Tsinghua University Press, 2006: 229−231.

Dynamic performance analysis of substructure for concrete girder bridges under vehicle braking

YANG Tingting1, LI Yan2, LI Quanlin3

(1. School of Civil Engineering, Harbin Institute of Technology, Harbin 150090, China; 2. School of Transportation Science and Engineering, Harbin Institute of Technology, Harbin 150090, China; 3. Shenzhen Highway Engineering Consulting Company, Shenzhen 518094, China)

The change of the braking coefficient was assumed as a time-varying slope function and the time-varying braking force of each wheel was distributed by using the deformation compatibility condition and force balance equation. Then the vehicle-bridge coupling dynamic analysis model considering braking load was established and the corresponding calculating program was built. Based on a concrete girder bridge, the dynamic behavior of the bridge under the action of vehicle braking was analyzed with the program. The influence factors such as initial velocity, braking acceleration rise time, peak braking factor and vehicle weight on dynamic response of bridge piers were studied. The results show that the longitudinal vibration response of pier top is significantly affected by the braking effect. With the reduction of the braking acceleration rise time, the increase of peak brake factor and vehicle weight, the longitudinal response of the pier increases greatly. The initial velocity has an effect on it, but there appears no linear relationship.

concrete girder bridge; vehicle and bridge coupled vibration; vehicle braking; substructure; dynamic analysis

U441.3

A

1672 − 7029(2020)03 − 0637 − 08

10.19713/j.cnki.43−1423/u.T20190460

2019−05−27

国家自然科学基金资助项目(51108132)；黑龙江省自然科学基金资助项目(LH2019E049)

李岩(1978−)，男，黑龙江依安人，副教授，博士，从事桥梁结构振动研究；E−mail：liyan2011@hit.edu.cn

(编辑 阳丽霞)