基于博弈论和证据理论的桥梁加固方案优选研究

孔令楠，郝伟

基于博弈论和证据理论的桥梁加固方案优选研究

孔令楠，郝伟

(兰州交通大学 土木工程学院，甘肃 兰州 730070)

为了更加合理地选择桥梁加固方案，处理方案优选过程中的不确定信息以及避免主观偏好性对决策的影响，提出基于博弈论和D-S证据理论相结合的加固优选方法。采用基于博弈论的组合赋权，确定科学合理的综合权重，结合西北干寒地区桥梁病害，以待评方案为辨识框架，根据加固效果目标，选取效果可靠性、经济合理性、施工技术可行性等3个2级指标，14个3级指标作为证据体，利用灰色关联法确定各证据体的确定信度，通过D-S证据理论融合规则，由信度函数值排序得到方案排序。结合西北地区某桥梁加固实例，研究结果表明：该模型在桥梁加固方案优选应用中有效性显著，比选结果可靠合理，大大提高了决策的准确性和方案间的区分性。

桥梁加固；博弈论；D-S证据理论；方案优选

随着我国公路交通运输网的不断发展和完善，行车密度和大型载重车辆不断增长，而早年较低的建造标准和维修养护意识的缺失，导致许多公路桥梁在设计寿命周期内劣化严重，桥梁可靠性要求严重不足。同时西北地区经济相对落后，自然条件恶劣，危旧桥数目之庞大，使得在面对公路交通运输业的发展需求和危旧桥梁、加固、改造两者之间的矛盾时，如何利用有限的资金合理进行旧桥加固方案的决策，最大化的达到经济使用寿命，保障公路建设可持续发展这一问题变得更为突出。桥梁加固方案的优选是一个典型的复杂多目标决策问题(影响加固效果的因素复杂、定性指标与定量指标兼含、量纲不一致等)，目前，学者们对多目标决策问题进行了深入研究。梁东等[1]通过区间数决策模型，得到了基于区间数距离的铁路线路决策方案排序；邱自学等[2]将模糊层次分析法与灰色关联法相结合，建立了多目标决策模型，对数控机床横梁设计方案的比选研究起到了指导意义。同时诸多学者结合多目标决策思想与桥梁加固方案优选进行了研究。杨永清等[3]针对桥梁加固方案评价过程中指标的不确定性和模糊性建立了以模糊数学理论为基础的不确定AHP方案评价模型，得到了合理可靠的决策方案；姜禹等[4]针对桥梁加固这一多目标决策问题，基于赋权关联度法，对主梁加固的4种方法进行了合理的比选；刘超等[5]通过数值分析和加载试验对空心梁桥铺装层2种加固方案的破坏模态和铺装层的应力比选得到较优方案。上述关于桥梁加固方案优选的研究中，采用模糊数学理论的定量分析方法相对缺乏对目标决策的客观性，由仿真模型得到的优选方案对加固方案定性指标的考虑又比较欠缺，而且上述模型中对比选方案间的多维信息的分析和融合较为缺乏，这些在较大程度上影响了方案比选结果的可信性和准确性。本文基于博弈论组合赋权和D-S证据理论，针对西北干寒地区桥梁病害，建立指标体系，在对主客观权重进行均衡博弈获取科学合理权重的基础上，引入D-S证据理论对方案多维信息进行融合，减少由于定性指标主观判断带来的累计误差，来提高决策的准确性，从而获取可信满意的方案，避免误选。

1 建立桥梁加固方案优选评价指标体系

由于桥梁加固方案优选的影响因素繁多，指标之间互不相容，使得构建一套更适合于西北干寒地区桥梁加固方案优选的评价指标体系用于科学合理的比选方案显得尤为重要。现通过参考相关文献[6−8]，根据《公路桥梁加固设计规范J22—2008》[9]及相关文献[10]，建立如表1所示的三层级评价指标体系。该指标体系具有如下特点：西北干寒地区恶劣的气候环境使桥梁结构多出现冻胀、裂缝、钢筋锈蚀等病害，因此效果可靠性中充分考虑了气候环境对桥梁病害及劣化的影响和加固后桥梁的安全性，耐久性以及适用性，大大增强了指标的普适性；方案的经济合理性以寻找桥梁寿命周期内效益的平衡点为目的，全面考虑了加固方案带来的效益和加固所需的直接与间接费用(中断交通等)。由于不同加固方案的施工措施受客观条件的制约，同时施工技术的成熟、适用性等很大程度上影响着施工的进度和质量，因此，将施工技术也作为指标评价准则层。

表1 桥梁加固优选方案评价指标体系

2 基于博弈论的组合赋权

科学合理的确定指标的权重对正确指导方案比选具有重要的意义。基于博弈论的组合赋权[11−12]，以纳什均衡理论为基础，目的在于将主、客观权重进行合理化的协调，从而降低主观赋权的任意性和客观赋权的绝对性，使得权重的确定更加贴近实际，更好的指导解决实际问题。

2.1 单一赋权法对指标赋权

采用表2中的主、客观单一赋权方法分别对指标求取权重。

2.2 基于博弈论确定综合权重

1) 用种不同赋权方法对指标赋权，构造基础权重向量集：

式中：为某一综合权重向量；λ为线性组合系数。

得到最满意的综合权重向量为：

表2 单一赋权法步骤

3 基于灰色关联和D-S 证据理论的方案优选计算模型

3.1 D-S证据理论

D-S证据理论以其处理不确定信息的优越性在信息合成中被广泛应用。通过证据合成规则来融合多个证据体的Mass(信度函数)函数，由得到的新的Mass函数确定证据体置信度的大小从而实现信息的融合，降低决策事件的不确信性[13−15]。定义如下：

则为Θ上的基本概率分布函数，即Mass 函数。

3.2 灰色关联法确定信度

采用何种方式确定Mass函数从而利用D-S规则有效融合各指标信息是证据理论的核心，而灰色关联法明晰的思路，还可一定程度上减少方案间信息不对称带来的损失，故本文采用灰色关联法来求解mass函数。

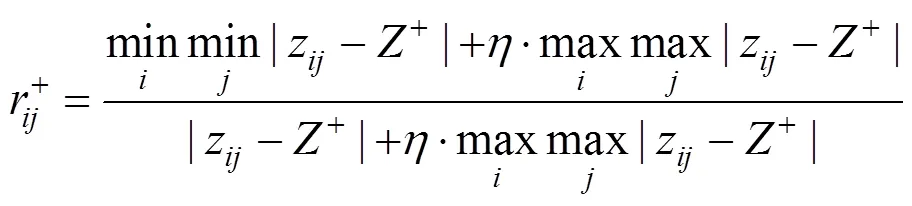
通过灰色关联系数可确定指标的2阶不确定度为：

那么指标下不同方案的Mass函数为：

整体不确信度的Mass函数值为：

3.3 D-S证据融合Mass函数

在Mass函数确定后，依据式(15)的证据融合法则对其进行不确信度的融合，从而降低方案的不确信性，可得不同方案的融合公式见式(14)：

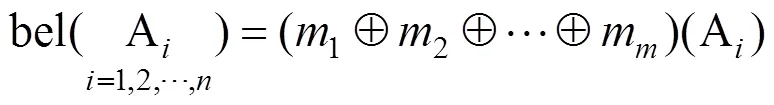
总体信度函数为：

由各方案的证据融合后的信度函数值排序即得到对应的桥梁加固方案排序。其中计算值最大的方案即为最优桥梁加固方案。同时可由式(15)得出方案决策整体的不确信度。这一融合过程通过对不确定信息的数学语言描述和推理融合，更好地降低了方案决策过程中的信息的不确定性，提高了比选结果的合理可信性。

4 案例分析

4.1 项目背景

本文以甘肃靖远三滩黄河大桥的加固为依托，进行分析和研究。三滩黄河大桥位于靖远县109国道上，始建于1999年，其主跨跨径为140 m，桥面铺装为钢纤维混凝土刚性路面，桥梁为双向4车道的跨河大桥。经统计由北向南的车道主要通行车辆为重载车辆，而由南向北的通行车辆轴重相对较小。当前经桥梁检测发现，桥梁重载车道铺装层出现了大面积纵向裂缝及45°斜向裂缝(图1)，并在跨中位置出现了较宽的横向裂缝(图2)。且当前跨中桥面铺装标高小于原桥面标高，桥面平整度较差。桥面铺装经钻孔取样发现，与梁板接触的最下一层铺装层与梁板脱空，且整体呈粉碎状态。以上桥梁病害严重威胁到了行车的安全性和舒适性。初步分析病害成因为桥墩基础下沉导致的桥梁整体线形变形较大，进而引起的铺装层和桥面板脱空，其次，重载车辆对桥面较大的冲击动荷载加速了桥梁病害的发展。

图1 重载车道纵向裂缝

图2 重载车道45°斜向裂缝

图3 跨中位置横向裂缝

通过分析桥梁病害原因，在结合现场条件和经济等因素的前提下，提出了4种可行的加固方案[16]。方案1：将桥面原刚性混凝土铺装层换成沥青混凝土柔性铺装层；方案2：在方案1更换铺装层的基础上，在铺装层与梁板之间增加环氧沥青黏结剂，并在桥梁主跨负弯矩较大处植入受拉筋；方案3：处理桥梁病害部分基础，更换病害部分桥墩，并按方案1方法对铺装层进行加固维修；方案4：旧桥只按方案1更换铺装层处理，降低使用等级，供轻轴重车辆行驶，并在旧桥原址附近修建新桥，专供重载车辆行驶。

4.2 权重确定

对桥梁加固方案各指标权重的计算可通过不同的权重计算方法得到，其中，G1法由专家对指标主观排序进行计算得到；熵值法根据各加固方案指标值量化形成决策矩阵，规范化后根据公式计算得出；由2.2节可得权重线性组合系数*= (0.287 2, 0.712 8)，各方法权重计算结果详见表3。

表3 不同方法的各指标权重

4.3 加固方案优选模型计算

由建立的桥梁加固指标体系，除指标k16，k23，k31，k32和k33等为定性指标外，其余的定量指标参考文献[10]得到不同方案对应的指标值；对于定性指标的计算，参照文献[4]中的7级因素等级集={很差，差，较差，中，较好，好，很好}模糊处理，对应值域[0,1]上的评定值为[0.05, 0.20, 0.35, 0.50, 0.65, 0.80, 0.95]；即得到方案评价矩阵。将方案评价矩阵规范化后，与所求的的综合权重向量相乘可得加权隶属度矩阵，由式(8)~(10)可求得灰色综合关联系数矩阵：

则各指标的2阶不确定度可由式(11)求得：

则桥梁加固指标在方案时的Mass函数矩阵由式(12)得：

不确信度DOI(I)由于原始矩阵标准化的原因,等于各指标下整体不确定性Mass 函数。辨识框架Θ即方案集，Θ={A1,A2,A3,A4}由合成法则可得4个方案和整体的信度合成函数值：

4.4 决策结果对比分析

由以上计算结果可知，在证据合成的过程中使得整体不确信度函数值由其平均值0.036下降到了融合后的0.000 48，不确定性大大减小。加固方案优选顺序为A3＞A4＞A2＞A1，选用第3个加固方案时，信度函数值最大，因此最优方案为方案3。最劣方案为方案1。方案1，2虽然短期来看成本工期都较低，对加固场地，周围建筑物扰动性都很小，但加固质量难以保证，较发展变化的交通量承载力也无法很好地满足，加固后使用维护费用昂贵，使用寿命难以量化，后期隐患大；方案4摆脱旧桥约束，施工方便，新建桥梁结构安全、可靠，但所需的人力物力财力，修建期间的交通问题，绕行的时间成本，高昂的造价等又是新的难题。而方案3整体造价较前2个方案虽然较高，但相对方案4来说造价和工期相对更优，合理地利用了桥梁原有资源，且对病害根源进行了有效的防治，在保证旧桥修复效果的前提下，使经济及使用性能达到最大的协调与均衡。表5所示为不同方法评估结果，经对比分析：各方法方案间决策结果大致相似，采用IAHP法，加固方案间难分伯仲，差异性不明显，对决策者的主观偏好依赖较大；采用灰色关联法，虽在1，2与3，4方案间有一定区别，但仍然体现不出方案的优越性。而本文所用模型，通过对各方案信息有效融合，综合反映了不同方案的差异性，准确客观的确定各方案的确定信度，大大提高了决策的准确性。

表5 各方法评估结果对比

5 结论

1) 基于西北地区干寒性气候对桥梁的影响而形成的普遍的特殊病害，所建立的桥梁病害加固方案优选指标体系适用性强；对西北地区桥梁加固方案的评价与优选有较强的指导意义。

2) 加固方案间的有效信息通过证据理论的有效融合，综合反映了不同加固方案对桥梁整体的共同作用，提高了决策的精确度。在证据合成的过程中使得整体不确信度函数值由平均值0.036下降到融合后的0.000 48，不确定性大大减小。

3) 采用证据理论和博弈论构建的桥梁加固方案优选模型和实际情况相吻合，说明该方法切实可行，对西北地区危旧桥加固对策研究的应用前景广阔。

[1] 梁东, 李远富, 樊敏. 基于区间数距离的铁路线路方案决策模型与方法[J]. 西南交通大学学报, 2019, 54(4): 823−830. LIANG Dong, LI Yuanfu, FAN Min. A decision making model and method base on distance measure between interval numbers in railway location[J]. Journal of Southwest Jiaotong University, 2019, 54(4): 823−830.

[2] 邱自学, 高志来, 任东, 等. 桥式龙门铣床横梁方案设计及其多目标决策方法[J]. 计算机集成制造系统, 2019, 25(10): 1−18. QIU Zixue, GAO Zhilai. REN Dong, et. Study on design of crossbeam scheme and its multi-objective decision-making method for bridge gantry milling machine[J]. Computer Integrated Manufacturing Systems, 2019, 25(10): 1−18.

[3] 杨永清, 杨灯, 余取. 基于不确定AHP的桥梁加固方案模糊综合评价[J]. 西南交通大学学报, 2019, 54(2): 219− 226, 216. YANG Yongqing, YANG Deng, YU Qu. Fuzzy comprehensive evaluation of bridge reinforcement scheme based on uncertain AHP[J]. Journal of Northwest Jiaotong University, 2019, 54(2): 219− 226, 216.

[4] 姜禹, 郝伟. 基于赋权关联度法的桥梁加固方案优选研究[J]. 铁道科学与工程学报, 2016, 13(7): 1317− 1322. JIANG Yu, HAO Wei. Research on bridge reinforcement scheme optimization based on empowerment relational degree[J]. Journal of Railway Science and Engineering, 2016, 13(7): 1317−1322.

[5] 刘超, 邹宇罡, 赵正. 同济路立交桥空心板梁桥加固方案比选[J]. 桥梁建设, 2018, 48(4): 118−123. LIU Chao, ZOU Yugang, ZHAO Zheng. Comparison of reinforcement schemes for hollow slab beam bridge of Tongji road overpass[J]. Bridge Construction, 2018(4): 118−123.

[6] 孙艳云. 干寒地区混凝土梁桥病害机理分析及耐久性评估[D]. 兰州: 兰州交通大学, 2018. SUN Yanyun. The disease mechanism analysis and durability evaluation of concrete beam bridges in arid and cold region[D]. Lanzhou: Lanzhou Jiaotong University, 2018.

[7] 黄建. 基于多属性群决策的桥梁加固方案比选研究[D]. 重庆: 重庆交通大学, 2013. HUANG Jian. Study on comparison and selection of bridge reinforcement schemes based on multi-attribute group decision making[D]. Chongqing: Chongqing Jiaotong University, 2013.

[8] XIE H B, WU W J, WANG Y F. Life-time reliability based optimization of bridge maintenance strategy considering LCA and LCC[J]. Journal of Cleaner Production, 2018, 176: 36−45.

[9] JTG/T J22—2008, 公路桥梁加固设计规范[S]. JTG/T J22—2008, Specifications for strengthening design of highway bridges[S].

[10] 赵丹. 西北干寒地区桥梁加固方案优选研究及应用[D].兰州:兰州交通大学, 2017. ZHAO Dan. Research on reinforcement scheme optimization and application of the bridge in the arid and cold region of north-west China[D]. Lanzhou: Lanzhou Jiaotong University, 2017.

[11] WEI X, DUAN H, WANG Y. Hybrid game theory and D-S evidence approach to multiple UCAVs cooperative air combat decision[C]// International Symposium on Neural Network, Springer, Berlin, Heidelberg, 2009.

[12] LIANG X F, XU Y. Reinforcement planning decision of old bridge based on TOPSIS-AHP method[J]. Advanced Materials Research, 2014, 919−921: 426−429.

[13] 李嘉良, 马东辉, 王威. 基于证据理论和熵权灰色关联的潜在地震滑坡危险性评价[J]. 中南大学学报(自然科学版), 2016, 47(5): 1730−1736. LI Jialiang, MA Donghui, WANG Wei. Assessment of potential seismic landslide hazard based on evidence theory and entropy weight grey incidence[J]. Journal of Central South University (Science and Technology), 2016, 47(5): 1730−1736.

[14] Shafer G. A mathematical theory of evidence turns 40[J]. International Journal of Approximate Reasoning, 2016, 79: 7−25.

[15] LÜ W. Decision-making rules based on belief interval with D-S evidence theory[C]// Fuzzy Information & Engineering, Second International Conference of Fuzzy Information & Engineering, Icfie, May, Guangzhou, China. DBLP, 2007.

[16] 朱定, 李书亮.港珠澳大桥钢桥面铺装方案比选及浇注式沥青混合料(GMA)标准化施工工艺控制[J]. 中外公路, 2019, 39(2): 161−164. ZHU Ding, LI Shuliang. Comparison and selection of steel deck pavement scheme for Hong Kong-Zhuhai- Macao Bridge and Standardized construction technology control of cast asphalt mixture (GMA)[J]. Journal of China and Foreign Highway, 2019, 39(2): 161−164.

Optimum selection of bridge reinforcement scheme based on game theory and evidence theory

KONG Lingnan, HAO Wei

(School of Civil Engineering, Lanzhou Jiaotong University, Lanzhou 730070, China)

In order to select the bridge reinforcement scheme more reasonably, deal with the uncertain information in the optimization process and avoid the influence of subjective preference on decision-making, a reinforcement optimization method based on the combination of game theory and D-S evidence theory is proposed. Combination weighting based on game theory is adopted to determine scientific and reasonable comprehensive weights. Combining with bridge diseases in dry and cold regions of Northwest China, the scheme to be evaluated is taken as identification framework. According to the goal of reinforcement effect, three secondary indicators, namely, effect reliability, economic rationality, feasibility of construction technology, are selected, and 14 third-level indicators are taken as evidence bodies. The grey correlation method is used to determine the reliability of each evidence body. The D-S evidence theory is used to fuse the rules. Finally, the reliability function is used to rank the schemes. Combining with a bridge reinforcement example in Northwest China, the results show that the model is effective in the optimization of bridge reinforcement schemes, and the results are reliable and reasonable, which greatly improves the accuracy of decision-making and the distinction between schemes.

bridge reinforcement; game theory; D-S evidence theory; optimal scheme selection

U445.72

A

1672 − 7029(2020)03 − 0556 − 07

10.19713/j.cnki.43−1423/u.T20190443

2019−05−21

长江学者和创新团队发展计划滚动资助项目(IRT-15R29)

郝伟(1970−)，女，陕西西安人，副教授，从事工程项目管理与工程经济研究；E−mail：gslzhaowei@ sina.com

(编辑 涂鹏)