基于分段拟合的致密气藏递减分析方法

刘会会，崔越华，吴 优，江乾锋，杨 辉

（1.中国石油长庆油田分公司勘探开发研究院，陕西西安 710018；2.低渗透油气田勘探开发国家工程实验室，陕西西安 710018）

Arps 递减曲线[1-3]以其简捷易用、所需数据少且易于获得等优势，成为目前油气藏工程中进行油气井产量变化规律分析及预测最常见的方法。Arps 的适用条件之一：气井处于边界控制流阶段。尤其是致密气藏的气井，有很长时间的不稳定流阶段，若对该阶段的生产数据应用Arps 递减曲线进行产量预测与指标评价，会存在较大误差。文献[4-6]提出：对于致密气藏有限边界压裂气井，随着流动阶段的变化，递减指数呈现“急速上升、持续下降、趋于稳定”的变化趋势。达到边界控制流以后，递减指数趋于稳定，产量变化规律也趋于稳定。根据前人的研究成果及Arps 递减曲线的适用条件，针对苏里格致密气藏压裂气井生产实际，提出其产量递减分析的关键—分段拟合，即以是否达到边界控制流为分界点，研究不同阶段气井产量变化规律。

1 致密气藏压裂气井数值模型的建立

应用产量不稳定分析法[7-10]，对苏里格气田苏X 区块315 口致密气井生产动态历史数据进行拟合，并结合该区域试井解释参数，得到不同类型气井所对应地层参数、井筒参数和生产参数的平均值（见表1），建立致密气井数值模型（以Ⅰ类井为例展示，见图1），模拟定压条件下单井产量变化规律。

图1 致密气藏压裂气井数值模型

表1 苏里格气田苏X 区块三种不同类型井平均参数表

2 确定气井到达边界控制流时间的方法

2.1 单井到达边界控制流时间模拟

判断气井生产是否处于边界控制流阶段是应用Arps 递减曲线进行产量递减分析的前提。根据试井理论中边界在压降试井双对数特征曲线中的反映[11，12]，采用上述建立的模型，进行试井设计[13，14]，获取压降过程的双对数曲线（见图2），可知：压力波传播至储层边界后，经过一段时间的压力过渡阶段后，进入稳定的阶段，可以看出压力的双对数曲线斜率变为1 并保持恒定，双对数曲线刚变为1 的时刻视为进入边界控制流的时间。依据该方法模拟得到苏里格气田Ⅰ、Ⅱ、Ⅲ类井到达边界控制流的时间分别为200 d～360 d、600 d～820 d、860 d～1 200 d（见图2）。

2.2 单井到达边界控制流时间计算方法

Craft 和Hawkins 于1945 年指出，油气藏开始受到边界控制流影响的时间和其半径有关，并且与扩散常数成反比，近似计算公式[15]为：

式中：tpss-边界控制流时间，d；φ-孔隙度，%；μ-黏度，mPa·s；ct-压缩系数，psi-1；re-控制半径，ft；K-渗透率，mD。

将苏里格气田压裂气井数值模型模拟的边界控制流时间，通过数学回归，对公式（1）进行校正，得公式（2）。

图2 压裂气井压降试井双对数曲线

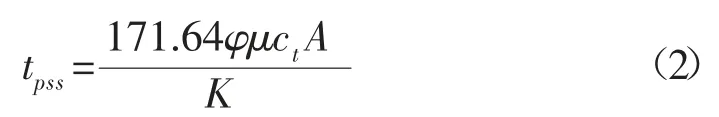
式中：tpss-边界控制流时间，d；φ-孔隙度，%；μ-黏度，mPa·s；ct-压缩系数，MPa-1；A-单井控制面积半径，m；K-渗透率，mD。

通过此公式可以方便的计算出单井到达边界控制流所需要的时间。

3 分段拟合递减分析方法

基于Arps 递减模型的分段拟合递减分析方法的核心是以气井生产到达边界控制流为分界点，对未达到边界控制流阶段、达到边界控制流阶段的气井分别进行指标初步预测及产量变化规律研究。

3.1 边界控制流阶段

对于生产时间较长、地层压力波及范围已经到达边界的气井，取边界控制流阶段生产数据，对比不同递减模型的预测效果。以模型拟合曲线的吻合程度和模型预测的可采储量拟合值与模拟值之间的相对误差作为评价模型拟合效果的指标，认为吻合程度高并且相对误差小于10 %时模型可靠，具体做法如下：

（1）同未达到边界控制流阶段做法（1），确定气井的可采储量，为理论值；

（2）利用上述公式计算模型到达边界控制流时间，取边界控制流时间的一倍、三倍、五倍、十倍时间的生产历史数据（见图3），运用Arps 不同的递减类型分别进行产量变化趋势拟合与可采储量预测；

（3）对比可采储量预测值与理论值之间的误差及曲线拟合吻合程度（见表2），确定最佳递减模型，进一步进行产量递减规律分析与预测。

对致密气藏苏里格气田不同类型气井均做上述分析，从拟合效果对比分析结果来看，不同类型气井递减规律和适用递减模型一致，均是采用衰竭模型预测的结果更可靠，预测曲线拟合度更高，预测可采储量误差均小于10 %，并随着生产数据量的增多，相对误差逐渐减小，说明生产历史数据越多，拟合越可靠。

3.2 实例分析

选取致密气藏苏里格气田典型气井分别进行整体拟合预测与分段拟合预测。以苏X 井为例进行说明，该井孔隙度为12 %，应用产量不稳定分析法建立该井数值模型，模型渗透率为0.1 mD，控制面积为0.28 km2，预测可采储量1 892×104m3，利用上述公式计算得到该井达到边界控制流时间为562 d。整段拟合。

预测可采储量1 564×104m3，与产量不稳定分析法得到可采储量相差较大，且预测曲线与实际生产数据偏差较大（见图4）；取该井边界控制流阶段的生产数据，以递减指数为0.5（衰竭递减）进行拟合预测，可采储量为1 828×104m3，与产量不稳定分析法得到可采储量相近，并且预测曲线与实际生产数据较为吻合（见图5），可以快速准确预测该井产量变化规律及生产指标。

图3 模型拟合数据体的选取

表2 Ⅰ类直井产量递减模型拟合效果

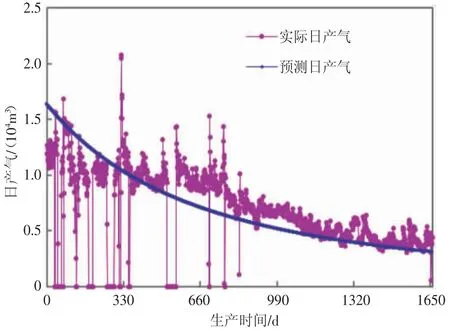
图4 苏X 气井整体拟合曲线效果

图5 苏X 气井分段拟合曲线效果

4 结论

（1）对于致密气藏压裂气井，应用Arps 递减模型进行产量变化规律分析时，必须以边界控制流为分界点，分段进行拟合预测，苏里格气田Ⅰ、Ⅱ、Ⅲ类井到达边界控制流的时间分别为200 d～360 d、600 d～820 d、860 d～1 200 d；

（2）对于达到边界控制流阶段的不同类型气井，产量变化规律符合Arps 的衰竭递减模型，即递减指数为0.5 的双曲递减模型，且生产时间越长，指标预测结果越可靠。