最大相关熵准则下多层极端学习机的批量编码

刘兆伦，武 尤，王卫涛，张春兰，吴 超，刘 彬，

1(燕山大学 河北省特种光纤与光纤传感重点实验室，河北 秦皇岛 066004)2(燕山大学 信息科学与工程学院，河北 秦皇岛 066004)3(燕山大学 电气工程学院，河北 秦皇岛 066004)

1 引 言

近年来，为了克服基本极端学习机(extreme learning machine，ELM)及其改进算法提取特征能力差[1]，难以有效处理图像、视频等自然信号的问题[2]，基于稀疏编码的多层极端学习机(HELM)作为一种多层神经网络被提出[3]，其与传统的叠加式自动编码器(SAE)相比，训练时间可以从小时缩短到秒[4]，在图像处理[5-8]和非线性模型辨识[9，10]等领域得到了广泛的研究.但在其应用过程中，HELM暴露出一些明显且公认的缺点，即其在进行大样本数据集学习时所产生的巨大运行内存需求，以及当训练集中存在噪声等异常数据时，HELM的学习效果变差且过拟合现象明显.

HELM在运行过程中内存占用较大的主要原因是：为保证HELM的学习精度，其决策层中的隐含层神经元数量往往需要被设置得很大，这使得参与计算的特征矩阵维度升高，从而导致运行内存需求的剧增.目前学者们针对HELM内存需求大的问题也多从降低决策层特征矩阵维度这个角度出发，通过PCA等多种算法实现对HELM的决策层隐含神经元数量的缩减来提出改进，如Wong Chi-man等将核学习引入HELM中来减小运行内存[11]；Zhou Hong-ming等人利用主成分分析法逐层对隐含层输出的特征矩阵进行降维以降低内存占用[12]；Henríquez等人提出一种基于Garson算法的非迭代方法对隐含层神经元进行剪枝实现降低运行内存的目的[13].尽管这些方法均实现了减少运行内存的目的，但是增加的算法无疑会导致计算复杂度的上升和模型结构复杂度的增加，从而使运算时间变长、学习速度变慢.针对这一问题，Liang Nan-ying等人提出的一种在线极端学习机[14]，可以实时根据新到来的数据对输出层权重矩阵进行矫正更新，给极端学习机处理大样本数据提供了一种将训练数据分批次进行学习的方法，也为降低多层极端学习的模型复杂度提供了思路.

HELM在训练集中存在噪声等异常数据时，学习效果变差且易发生过拟合现象的原因是：HELM中的最小均方差准则(MMSE)默认数据误差呈高斯分布[15]，这在实际应用数据中这样的假设明显是不合理的.针对这个问题Xing Hong-jie等人提出了基于相关熵准则(MMC)的极端学习机[16]，提升了极端学习机应对异常数据的性能，降低模型对异常点的敏感性从而改善模型的过拟合问题.如Chen Liang-jun等人，用MCC准则代替传统多层极端学习机(multilayer extreme learning machines，ML-ELM)决策层中的MMSE准则，使ML-ELM的鲁棒性和过拟合现象得到改善[3].唐哲等人将MCC准则应用于半监督学习算法中，有效地提高了半监督学习算法的学习性能[17].Luo Xiong等人将一种堆叠式多层极端学习机(stacked extreme learning machine，S-ELM)中的MMSE准则替换为MCC准则，实现了S-ELM学习精度的进一步提高[18].这都为本文将MCC准则引入HELM决策层提供了理论基础和方法指导.

根据上述多层极端学习机现存的问题和在线极端学习机、相关熵准则等方法的启发，本文提出一种基于最大相关熵准则的批量编码式多层极端学习机.在原始多层极端学习机的决策层中引入最大相关熵准则，构建基于最大相关熵准则的多层极端学习机.基于最大相关熵准则的多层极端学习机(MCC-HELM)分批次对由大数据集分解得到的多个小数据集进行学习，接着利用在线极端学习机的方法，将多个批次的学习数据，在MCC-HELM的决策层实现融合，构成基于最大相关熵准则的批量编码式多层极端学习机(BC-HELM)，并得到最终的学习结果.最后通过仿真实验确定其网络参数并通过与其他多层极端学习机对比来验证其性能.

2 基于最大相关熵准则的批量编码式多层极端学习机

2.1 多层极端学习机与最大相关熵准则的结合

原始多层极端学习机由两部分组成：基于稀疏自动编码器的无监督特征学习和基于传统极端学习机的有监督决策[19].而决策层中传统极端学习机是基于MMSE准则来建立目标函数的，由于该准则对异常点极为敏感，传统极端学习机在应用过程中极易出现过拟合现象.于是本文将原始多层极端学习机决策层中的MMSE准则使用MCC准则代替，设输入的训练样本数为S，隐含层神经元个数为L到，得到新的目标函数：

(1)

(2)

式(2)中σ为尺度因子，τ为正则化参数。针对上述非线性优化问题，采用半二次优化技术通过迭代方法进行求解，目标函数为：

(3)

对式(3)进行求导得到：

(4)

根据半二次优化技术中的共轭凸函数理论[20]，式(4)中的高斯核的部分暂时使用对角矩阵中Λ表示即：

(5)

于是式(4)整理为矩阵形式变为：

(6)

由于多层极端学习机是针对大样本数据集的处理提出的，因此本文默认训练样本数远远大于隐含层神经元的数目，则对式(6)进行求解得到输出权值矩阵的表达式为：

β=[2τσ2I+HTΛH]-1HTΛT

(7)

于是得到迭代表达式：

(8)

式(8)中的对角矩阵Λ是根据半二次优化技术中的共轭凸函数理论建立的，来表示目标函数中高斯核的部分.其中对角矩阵Λt+1中的Λii对应第i组数据通过上一次迭代得到的输出权重βt而求得的学习输出与目标输出之间的距离；βt+1表示根据Λt+1中的距离更新得到的新的输出权重矩阵.设输出数据维度为m，设置一个转换矩阵φ∈(S×m)，令：

β=HTφ

(9)

同时将式(7)中等号右边求逆的部分换回等号左边，则式(7)重构为：

[2τσ2I+HTΛH]HTφ=HTΛT

(10)

将式(10)等号右边中的HT乘进括号中，等号两边便能够同时抵消掉最右边的HT，于是式(10)写为：

[2τσ2I+ΛHHT]φ=ΛT

(11)

由核函数理论可知，存在低维输入空间中的核函数k(x,x′)与高维特征空间中的內积〈φ(x)·φ(x′)〉相等[21]，即核函数用来代替式(11)表达式中的內积计算，则：

[2τσ2I+ΛK]φ=ΛT

(12)

同理，将式(9)的变换代入式(5)中，并将对角矩阵Λ中的內积计算由核函数形式代替，得到：

(13)

式(13)中Ki表示第i个数据对应隐含层输出的特征矩阵的內积hihiT，式(12)中K表示由Ki组成的对角矩阵，这里由于只需计算对角线上的数值，因此即使核变换导致运算矩阵的维度由L×L升高至S×S但是计算量却大大下降，避免了计算量因隐含神经元数目的增加而剧增的问题，于是经过式(9)变换后得到MCC-HELM的决策层即MCC-ELM的迭代公式为：

(14)

MCC-HELM结构如图1所示.

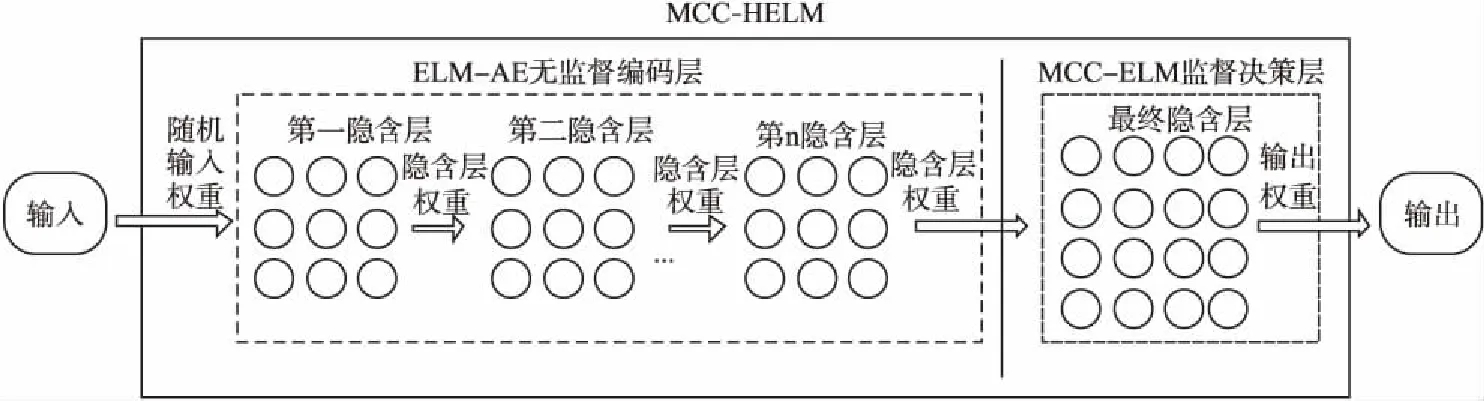
图1 MCC-HELM结构Fig.1 MCC-HELM network

2.2 最大相关熵准则下多层极端学习机批量编码的实现

在保证学习效果的前提下，训练数据的个数越多则需要的隐含层神经元数量越大.于是本文将训练数据平均分为D组，每组数据形成一个批次，分别通过MCC-HELM进行学习，从而降低每一个MCC-HELM对最后决策层中隐含层神经元数量的需求.最后将在线极端学习机的方法引入进来，将当前组的MCC-HELM的决策层与历史组数据的MCC-HELM决策层结合再完成决策.这样一来，每一次的决策都是在综合历史训练数据通过多层稀疏自动编码器学习到的所有特征信息的基础上进行的，因此保证了学习结果的可靠性，达到保证精度的同时缩小内存需求的要求.

由于在融合决策阶段涉及到整体求逆的问题，为了减小求逆的时间，不再进行式(9)以及核矩阵的转换，仍然转换为原始极端学习机中当训练数据远远大于隐含层神经元时的输出权重表达式的形式，从而减小融合决策时需要进行求逆的矩阵的维度，缩短计算时间。用A表示由各批次数据的迭代结果Λ所组成的融合对角矩阵，即式(14)迭代运算中的φ只为了求得更优的Λ，来用于融合进A中，而融合得到的A则代回式(7)求得最终的β。

于是假设多层极端学习机由两层稀疏自动编码器和一层基于最大相关熵准则的极端学习机构成，以批次数为3做例，将训练数据平均分为3组，分别使用D1、D2、D3来表示。将D1输入MCC-HELM1中，得到多层极端学习机决策层的隐含层输出的特征矩阵Η31，并迭代求得第一部分训练数据D1所对应的输出权重矩阵β1；同理分别将D2、D3输入MCC-HELM2、MCC-HELM3中，得到多层极端学习机决策层的隐含层输出Η32、Η33。本文提出一种批量编码式MCC-HELM的结构，对D组训练结果进行融合决策。对于数据D1来说，根据2.1内容所示令：

H1=H31

A1=Λ1

其中Λ1表示数据D1通过半二次优化技术迭代求得的对角矩阵，则：

(15)

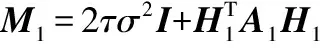
(16)

将第2批数据求解得到的特征矩阵Η32与第1批数据求得的特征矩阵Η31结合，得到Η2：

同时，通过式(14)的迭代得到Λ2，于是：

则得到：

(17)

式(17)右侧求逆部分用M2表示，则：

(18)

式(17)右侧非求逆部分可表示为：

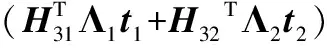
(19)

于是得到：

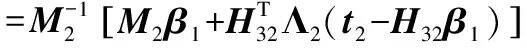
(20)

同理，依次将每一批训练数据对应的MCC-HELM决策层中隐含层输出进行融合，得到MCC-HELM最终的迭代表达式：

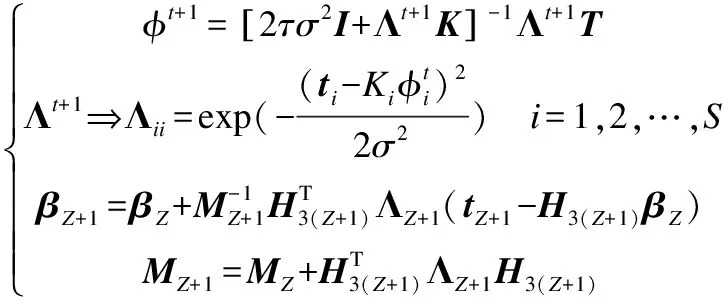
(21)

式(21)中，t表示每一批数据的迭代次数，Z表示已输入的数据批次数；每对一批训练数据进行融合和学习，输出权重矩阵β就被优化并更新一次，最终得到一个包含对所有训练数据学习得到的信息的最优输出权重矩阵βfinal.在测试阶段，将测试数据全部输入MMC-HELM中，得到Η3t.直接通过式(22)得到预测输出：

Y=H3tβfinal

(22)

基于最大相关熵准则的批量编码式多层极端学习机结构如图2所示.

3 实验仿真

本论文的数值计算得到了燕山大学超算中心的计算支持和帮助，均是基于Intel E5-2683v3(28核)@2.0GHz，64GB RAM，Centos7.2，使用Matlab R2018a仿真软件进行的.以MNIST、NORB两个深度学习最常用的大样本数据集为例对本文所提出的BC-HELM进行参数的选择并与其它多层极端学习机进行性能对比.其中MNIST数据集由250人的手写数字图像构成，是最常用的合理性检验数据集；NORB数据集为以不同照明及摆放方式摄制玩具模型的双目图像，是常用的图像分类数据集.具体信息如表1所示.

3.1 参数选择

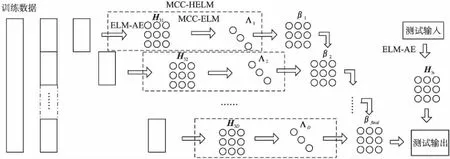
图2 基于最大相关熵准则的批量编码式多层极端学习机结构图Fig.2 Structure of batch coded hierarchical extreme learning machine based on maximum correntropy criterion

表1 数据集信息
Table 1 Data set information

数据集特征数训练样本数测试样本数类别MNIST28∗28600001000010NORB1024∗224300243005

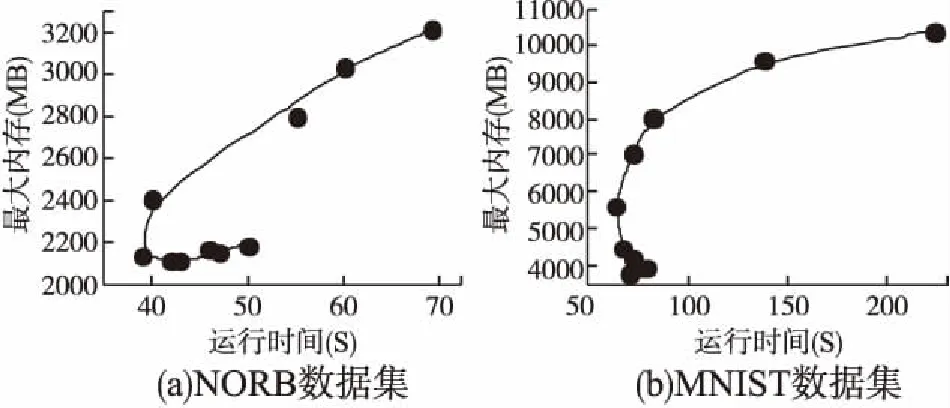
图3 不同批次数性能对比Fig.3 Performance comparison of different batches

从图3可以看到，对于最大内存占用：当批次数变大时，由于每次输入的训练样本数变小，使得最大内存占用也会相应减小.对于运行时间：当批次数变大时，每次输入的训练样本数变小，参与计算的矩阵维度减小，使得计算时间降低，但是同时，不同批次的训练结果依次进行结合的过程需要额外的计算，因此随着批次数的增加，这部分额外计算所需要的时间也将变大，因此，由于矩阵维度降低而缩短的计算时间大于多个训练批次结合的计算时间时，运行时间将会下降，反之，运行时间将会上升.于是随着批次数的增加，最大内存占用将呈现逐渐减小的趋势，而整体运行时间将会出现先下降后上升的情况.因此需要通过实验来折中选取每个数据集对应最佳的批次数，即最大内存占用尽量少的同时运行时间也较低的情况.图3(a)对应NORB数据集将批次数依次设置为1-10时所占用的最大内存和运行时间，可以看出当批次数为5的点是最接近原点的点，即将训练样本分成5个批次进行训练时，内存占用与运行时间都较低是最佳的情况.同时，由于测试样本数相对较大(与训练样本数相同)，当批次数大于5时所占用的最大内存将产生于测试数据的运算过程中，因此呈现较为平缓的趋势.图3(b)对应MNIST数据集将批次数依次设置为1-10时所占用的最大内存和运行时间，当批次数大于6时，训练样本数降至10000以下，小于测试样本数，所占用的最大内存将产生于测试数据的运算过程中，因此占用的最大内存趋于稳定，由于图3(b)中当批次数为7、8、9、10对应的点相距较近，因此将这5种情况在表2中详细列出进行对比与选择.

表2 MNIST数据集的相近批次数性能对比
Table 2 Performance comparison of similar batches under MNIST data sets

批次数运行时间(S)标准差最大内存(MB)标准差778.009.833948.55379.46875.0012.543921.14716.08972.008.634190.761026.071070.007.033909.84243.19

表2中标准差数值的大小反映了每次运行的结果相对于均值的离散程度，标准差越小，表示运行结果与均值的偏差越小.通过表2不难发现，对于MNIST数据集，批次数为7、8、9、10时相比，最大内存占用相当，而批次数为10时的运行时间最短，同时运行时间与最大内存分别对应的数据标准差也最小.因此综上所述，对于MNIST数据集将批次数设置为10，对于NORB数据集将批次数设置为5.将每个数据集的训练批次数确定后，每批次输入的样本个数即确定了，在此基础上通过实验可以得到BC-HELM的正则化系数C的数量级以及决策层隐含层神经元个数L与测试精度之间的关系.实验结果如图4、图5所示.

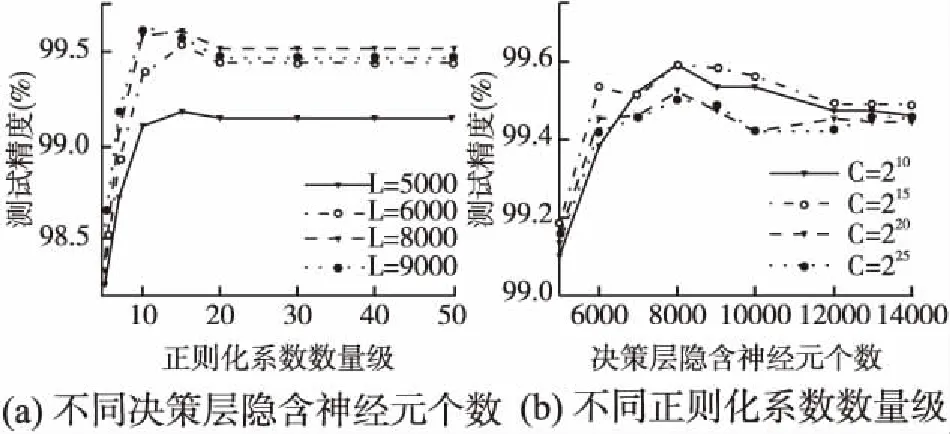
图4 MNIST数据集 BC_HELM在不同参数下性能对比Fig.4 Performance comparison of BC_HELM with different parameters data set MNIST data set

从图4可以看出，对于MNIST数据集，当C=220时(a)图中的不同L值对应的曲线开始趋于稳定，同时从(b)图中可以看出当L=8000时不同C值对应的曲线均达到最大值.即当L=8000时BC-HELM的精度在趋于稳定时达到最高，当L<8000时，测试精度随着L的增加而变大；当L>8000时，测试精度略低于L=8000时的精度，且随着L的增大，测试精度逐渐趋于稳定.从图5可以看出，对于NORB数据集，当C=215时(a)图中的曲线开始趋于稳定，同样从(b)图中可以看出当L=650时不同C值对应的曲线达到最大值.即当L=650时BC-HELM的精度趋于稳定时达到最高，当L<650和L>650时，测试精度随着L的变化现象与MNIST数据集对应相同.于是对于MNIST数据集将BC-HELM的正则化系数C设置为220，决策层隐含层神经元个数L设置为8000；对于NORB数据集将BC-HELM的正则化系数C设置为215，决策层隐含层神经元个数L设置为650.

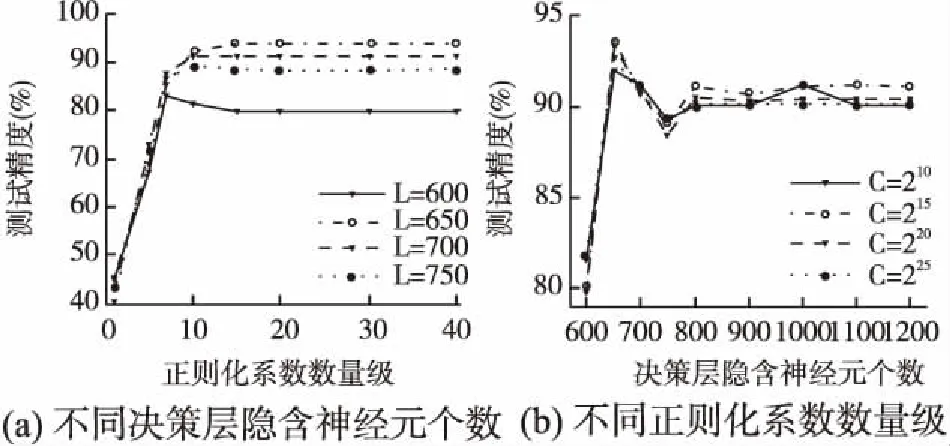
图5 NORB数据集 BC-HELM在不同参数下性能对比Fig.5 Performance comparison of BC_HELM with different parameters under NORB data set

3.2 与HELM比较

将所有参数确定后，将BC-HELM与HELM进行性能对比.同时表3中列出了BC-HELM与HELM的多方面信息进行对比.

表3 BC-HELM与HELM的性能对比统计
Table 3 Performance comparison statistics between BC-HELM and HELM

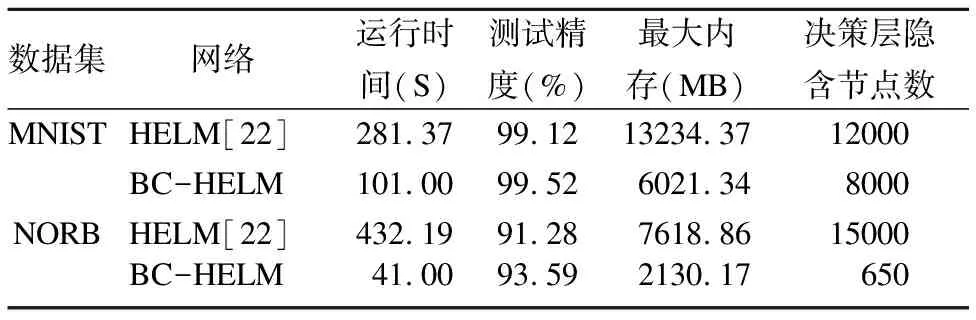
数据集网络运行时间(S)测试精度(%)最大内存(MB)决策层隐含节点数MNISTHELM[22]281.3799.1213234.3712000BC-HELM101.0099.526021.348000NORBHELM[22]432.1991.287618.8615000BC-HELM41.0093.592130.17650

根据表3中的统计数据可以得到，BC-HELM虽然与HELM有着相同的收敛特性，但相较与HELM，BC-HELM可以收敛于更高的测试精度.即与HELM相比，在MNIST数据集上测试精度提高0.4%，在NORB数据集上测试精度提高2.31%.这是由于MCC准则与HELM中MMSE准则相比降低了网络对异常点的敏感性，使网络的过拟合问题得到改善，因此测试精度有小幅度的提升.从决策层隐含节点数来看，训练数据分批次输入，使每次输入的训练样本数减小，这直接降低了数据对决策层节点数L的需求，因此在两个数据集上BC-HELM的决策层节点数均小于HELM.同理，对于占用的最大内存而言，BC-HELM与HELM相比，在MNIST数据集上降低54.50%，在NORB数据集上降低72.04%，这是由于输入的训练样本数减小，相当于将特征矩阵纵向降维，同时决策层节点数减少相当于对特征矩阵进行横向降维，双重降维后对特征矩阵的计算量将大大减小，也因此与HELM相比运行时间被大大缩短，分别在MNIST数据集上缩短64.10%，在NORB数据集上缩短90.51%.综上所述，BC-HELM相比于HELM，在保证测试精度的前提下，缩短了运行时间的同时大大降低了内存需求.

3.3 与其他多层ELM网络对比

下面针对运行时间与测试精度两个方面将BC-HELM与两种经典的多层ELM网络(文献[22，1])以及三种最新的多层ELM网络(文献[12，3，2])进行对比，统计结果如表4所示.

表4 BC-HELM与其他多层ELM的性能对比统计
Table 4 Performance comparison statistics between BC-HELM and other multilayer ELM

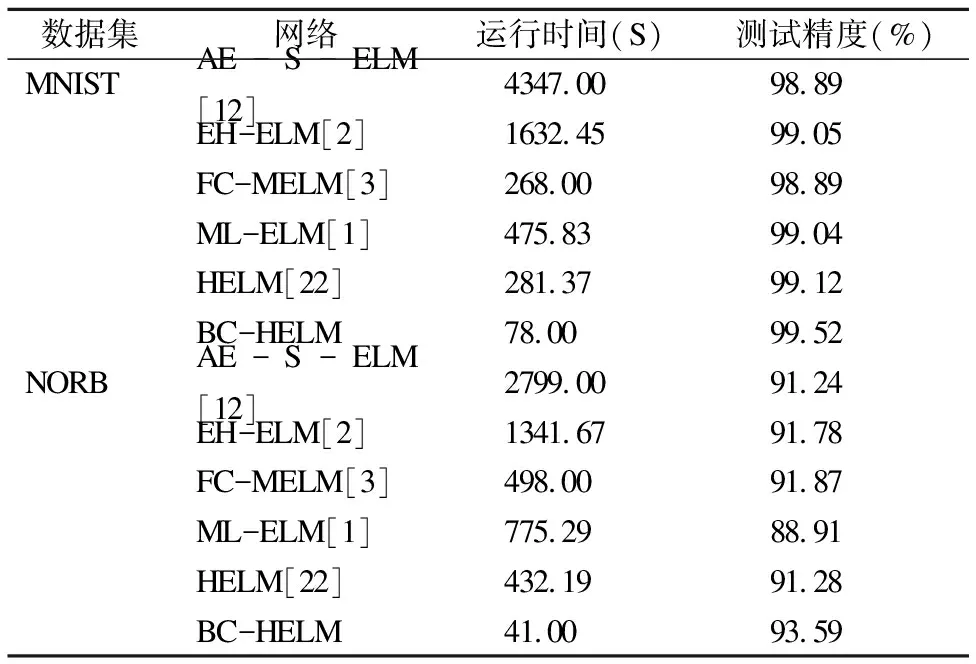
数据集网络运行时间(S)测试精度(%)MNISTAE-S-ELM[12]4347.0098.89EH-ELM[2]1632.4599.05FC-MELM[3]268.0098.89ML-ELM[1]475.8399.04HELM[22]281.3799.12BC-HELM78.0099.52NORBAE-S-ELM[12]2799.0091.24EH-ELM[2]1341.6791.78FC-MELM[3]498.0091.87ML-ELM[1]775.2988.91HELM[22]432.1991.28BC-HELM41.0093.59

从表4中数据可以得到，两种经典的多层ELM网络相比，HELM的运行时间在MNIST数据集上较ML-ELM缩短40.87%，在NORB数据集上较ML-ELM缩短44.25%，同时测试精度分别提高了0.08%和2.37%，这是由于在决策层中加入一层隐含层映射，使决策层变为原始极端学习机，相比于ML-ELM的决策层减少了自动编码的大量计算因此运行时间被缩短，也正因加入的隐含层映射，将编码层无监督学习到的结果映射至特征空间再进行有监督决策使测试精度提高，使HELM比ML-ELM具有更佳的学习性能.而3.2节中将HELM与本文提出的BC-HELM进行对比可以得到，BC-HELM具有比HELM更高的学习效率.

从三种最新的多层ELM网络数据来看，AE-S-ELM、EH-ELM两个网络在两数据集上的运行时间远远大于BC-HELM，较HELM也显著增加，这说明此两种多层ELM网络均存在着由于网络复杂度的增加而使运行时间被大幅增加的问题，而FC-MELM网络的运行时间虽然与HELM相比不相上下，但BC-HELM与之相比，在MNIST数据集上缩短70.90%，在NORB数据集上缩短91.77%，可见从运行时间来看，BC-HELM最佳.从测试精度来看，在MNIST数据集上，BC-HELM较AE-S-ELM提高0.63%，较EH-ELM提高0.47%，较FC-MELM提高0.63%；在NORB数据集上，BC-HELM较AE-S-ELM提高2.35%，较EH-ELM提高1.81%，较FC-MELM提高1.72%，即与三种最新的多层ELM网络相比BC-HELM的测试精度最高.综上可得，本文提出的BC-HELM与两种经典的多层ELM网络以及三种最新的多层ELM网络相比，运行时间更短且测试精度更高，具有更佳的学习效率.

4 结 论

本文构建了一种基于最大相关熵准则的批量编码式多层极端学习机--BC-HELM.将MCC准则应用于HELM的决策层中，避免了传统的MMSE准则对异常点敏感的问题，使HELM网络的过拟合现象得到改善，从而保证了分类精度.同时提出了一种对训练数据进行批量编码的学习方法，通过将训练样本批量学习的方式，减少输入网络的样本个数，降低了大样本数据对网络隐含层节点数的需求，使计算量随之大大下降，从而也降低了学习过程中所占用的最大内存与运行时间.实验结果表明，本文提出的BC-HELM与HELM相比，在保证测试精度的前提下，运行时间更短且内存需求也被大大降低；与其他多层ELM网络相比也具有更高的学习效率.