基于车联网的信号灯协同控制

李婉，班学钢*

a Oak Ridge National Laboratory,Knoxville,TN 37932,USA

b University of Washington,Seattle,WA 98195,USA

1.引言

在过去的几十年中，为了减轻日益严重的交通拥堵，人们已经在改善交通信号控制系统的性能方面进行了长期的努力。车联网（CV）技术在信号时序优化过程中受到越来越多的关注。这些技术包括了车对车（V2V）通信、车对基础设施（V2I）通信、车对行人（V2P）通信和车对万物（V2X）通信。通过车联网技术，我们可以获取驾驶员的信息，比如他们的出发地、目的地以及精确的轨迹信息（如每秒车速以及位置）等。此类信息可以传输到信号控制器以进行信号时序优化。车联网还有利于信号化干道或道路网络上多个交叉路口的信号协同控制，这可以大大提升车队通过相邻交叉路口的效率。信号灯协同控制有三个关键参数：周期时长（Cycle）、相位时长（Split）和相位差（Offset）。周期时长的定义为完成完整信号相位序列的时间段。通常，协同控制的交通信号必须具有相同的周期时长，即“公共周期时长”（或公共周期时长的一半或两倍的情况）。实际上，可以通过诸如SYNCHRO†http://www.trafficware.com/synchro.html和TRANSYT之‡https://trlsoftware.com/products/junction-signal-design/transyt/类的信号设计工具来确定这样的公共周期时长。相位时长是一个相位的绿灯时长与黄灯和红灯时长的总和，也是周期时长的一部分。相位差是相位周期中某个固定时间点（如绿灯时间的开始）与系统参考点之间的时间差。对于干道上相距较近的交叉路口而言，协同控制是非常有利的，因为这些相邻交叉路口之间的交通需求相对较大而且随机[例如，美国联邦公路管理局（FHWA）[1]提出的建议间距是1200 m]。

信号协同控制模型有一些常用的有效性度量（MOE）。带宽最大化曾经是信号协同控制常见的目标函数。这是指车辆在不停车的情况下经过协同控制干道所有路口的时间。带宽与系统饱和流量以及实时交通流量有关，后者由相位差决定。早期关于带宽优化的研究文献主要依靠图形法[1-4]，而后来的文献研究则集中在混合整数线性规划（MILP）上，以实现协同控制干道两个方向带宽之和的最大化[5]。分支定界算法通常用于解决优化问题。例如，Gartner等[6]扩展了以前的信号协同控制模型，在MILP公式中考虑了实际的交通流量和流量承载力，以实现带宽优化。他们的模型被称为多带模型（MULTIBAND），因为他们为干道的每个方向设定了不同的带宽，并根据它们对目标值的贡献单独加权。PASSER是一种软件工具，它可以在给定相位时长的情况下实现带宽效率的最大化[7]。其他有效性指标还包括延误、总行程时间、停车次数和排队情况等。Coogan等[8]通过假设每个交叉路口都有一个公共周期时长的固定配时方案，优化了协同控制交通信号的相位差。他们导出了一个非凸的、二次约束二次规划（QCQP）的闭式分析模型。模拟结果表明，队列长度显著减少。由于交通流量的随机性，行程时间的可靠性是衡量动态交通状况的另一个重要指标。Zheng等[9]将平均行程时间最小化及其可靠性作为优化固定周期时长、有效绿灯时间和相位差的目标。他们采用了基于遗传算法的方法来解决非线性优化问题。在模拟网络和实际干道当中，该模型能显著提高行程时间的可靠性并减少模拟和真实情况的延误。Hu和Liu[10]开发了一个数据驱动模型以实现主干道交通总延误的最小化。他们解决了两个问题：协同控制阶段的早期返绿问题以及交叉路口排队长度的不确定性。分解求解技术是解决网络级交通信号优化问题的常用方法[11-15]。尽管大多数分解方法并未将相位差视为其模型中的变量，但他们在优化交通网络的信号时序时会利用其协同控制特性。每个交叉路口的交通信号灯时序都是通过考虑交通条件的影响和大面积（如几个上游和下游交叉路口）的信号时序来确定的。因此，研究者同时考虑多个相邻交叉路口以改善系统运行。

随着车联网技术的出现，车辆（驾驶员）和交通基础设施可以实现信息实时交换。这些信息（如起点、目的地、出发时间和每秒运动的轨迹）可以被基础设施用来更好地更新交通信号时序，从而减少拥堵并提高燃料效率。Li等[16]开发了一个基于车联网环境中单个车辆轨迹的信号时序优化和协同控制模型。他们采用混合整数非线性规划（MINLP）对干道当中多个信号的绿灯时间和相位差进行了优化。Li和Ban[17]将单个交叉路口的交通信号优化问题归结为混合整数非线性规划问题。然后将其转化为一个动态规划（DP）问题，并采用两步的方法来确保动态规划得到的最优绿灯相位差为一个固定的周期时长。Beak等[18]为车联网环境中的自适应协同控制开发了双层优化模型。在交叉路口层，他们根据动态规划确定每个相位的最优绿灯时间。在干道交通层，他们对相位差进行优化以获得最小延迟。该模型可以降低协同控制相位和整个网络的平均时延以及停止次数。基于累积的行程时间，Lee等[19]在车联网环境下提出了一种实时交通信号控制方法。研究者利用Kalman滤波技术估计不同车联网渗透率下累积的行程时间。这些学者认为，该方法可以应用于主干道的信号灯协同控制。Li等[20]开发了一个双层优化模型来对网络中的交通信号时序进行优化。模型上层用于计算最优绿灯时间和相位差，以实现平均行程时间最小化的目的；而模型较低层的问题则是为了实现网络平衡而开发的。这些研究人员将双层优化问题分解为通过遗传算法（GA）和动态交通流量分配（DTA）解决的单级问题。Priemer和Friedrich[21]提出了一种车联网环境下多交叉路口的自适应交通信号控制方法。他们运用动态规划和枚举来优化信号定时参数，以便在不同车联网渗透率下减少接下来20 s的队列长度。Islam和Hajbabaie[22]开发了一种分布式交通协同控制方案。通过决定绿灯时间的终止或延续，他们将网络级决策问题的复杂性降低到单个交叉路口级问题的程度上。他们还在几个案例研究中评估了需求水平和车联网渗透率的影响。

当前，大多数交通信号时序优化和协同控制方法均采用集中式方案，各种类型的时序参数（相延续时间、周期时长和相位差）被集中在一个优化问题中同时求解，这可能会导致几个问题。首先，基于单个车辆的交通信号控制/协同控制问题通常具有较多的维数，并且是不确定性多项式（NP）完全问题（这类计算问题通常无法找到有效的解决算法）。其次，对于大型的交通干道或道路网络，信号时序优化和协同控制问题难以解决并且不适用于实时信号控制。一些学者试图通过将整个问题分解为几个可控的子问题来解决该信号优化问题。但是，这些研究所使用的周期时长大多是变化的[19-22]，因此不能直接应用于交通信号协同控制。

本研究的目的是在车联网环境中利用车对基础设施（V2I）以及车对车（V2V）通信来生成多个相邻路口的最优信号时序参数。我们假定干道中的所有车辆都已连接到基础设施（当车辆在交叉路口一定距离之内时），以便其轨迹（每一秒的速度和位置）可实时提供给信号控制器进行信号时序优化。这其中，我们将Li和Ban[17]的信号优化方法从单个交叉路口扩展到交通干道上多个交叉路口的优化协同控制当中。为了实现协同控制，多个交叉口的信号灯周期被设定为固定值。首先，我们将基于车联网的信号灯协同控制问题归结为MINLP。目标是通过计算最优的相位时长和相位差使得干道当中所有互联车辆的燃料消耗量以及行程时间同时达到最小化。由于MINLP模型的高维度，直接求解该问题具有一定挑战性。因此，我们将问题分解为一个基于车联网的交通信号双层优化模型，该模型包含单个交叉路口层和交通干道层（多交叉路口）。为对该双层优化模型进行求解，我们开发了一种基于预测的自适应方法，该方法收集每个周期开始时到达车辆的信息，并使用研究者在参考文献[23]中提出的动态规划（DP）方法计算每个交叉路口最优的相位时长。在计算过程中，我们会在每个路口确认其他路口的信号状态、车辆状态和“临时”最优相位差。这确保了主要干道上的车流量在相邻的道路交叉路口之间的协同控制。在交通干道层，我们对“临时”的相位差进行迭代计算，以便在总成本收敛到最小值时找到最优相位差。

本研究所提出的模型不同于Beak等[18]开发的双层优化方法。差异主要体现在以下几个方面。首先，在交叉路口层，Beak等应用了固定信号灯配时中的强制关闭选项，并在动态规划方法中增加了更多的协同控制约束条件以计算信号时序参数。该方法本身具有双层结构，这使得Beak等[18]采用的整体结构体系是一个三层模型。本研究所提出的模型使用Li和Ban[17,23]文中的DP来计算单个路口的最佳信号时序，其总和为固定的周期时长。在交通干道层，Beak等[18]开发了一个MILP，以使车队的延迟实现最小化。本文在确定最优相位差时考虑了单个车辆的轨迹，因此比参考文献[18]中的交通干道层模型考虑的路网和车辆信息更为全面。

这项研究在以下方面为该领域的研究做出了贡献：

（1）将交通信号优化与协同控制问题建立成混合整数非线性规划（MINLP），模型利用车联网技术提供的实时轨迹数据来优化信号灯配时方案；

（2）本文将基于MINLP的高维度集中式信号灯优化模型分解为双层优化控制模型，其中交叉路口层用于优化各个交叉路口的信号灯相位时长，而交通干道层用于计算信号灯的相位差；

（3）针对双层问题提出了一种基于预测的迭代求解方法。

2.交通信号灯协同控制

在干道或交通网络，交通协同控制为通过多个相邻交叉路口的车队能够平稳行进保驾护航。在本项研究中，我们的目标是实现沿协同控制方向（即在主干道上的）的所有互联车辆的燃料消耗和行程时间最小化，以计算干道的最优交通信号参数，即相位时长和相位差。如图1（a）所示，我们可以将底部交叉路口作为参考信号灯，并根据参考信号灯的信号操作来协同控制其他交叉路口。通常，相位差会保持一段时间（如30 min），并且可以根据实际交通状况进行变化。

本研究采用双环控制器，双环控制器由六个相位组合以及八个相位组成，如参考文献[23]所述，如图2（a）所示。假设东行（EB）和西行（WB）的直行方向是协同控制方向[图2（b）中第1相的移动2和6]，并且该相位不能为0 s。第2相和第3相不能同时实现，因为是冲突相位。同样的情况适用于第五组中的第6相和第7相。

2.1.将信号协同控制整理为混合整数非线性规划问题

图1.多路口的协同控制。（a）具有交通协同控制功能的道路示意图（数字1～8代表不同的行驶方向，E：向东）；（b）相位差图示（两个交叉路口之间的距离可以变化，如1000 m）。

图2.交通信号灯配置。（a）分组配置交通信号；（b）分相配置交通信号。

在作者先前开展的研究[17,23]中，单个路口的信号控制问题被表述为MINLP。它可以求得满足固定周期时长约束的最优相位时间。当考虑干道上多个交叉路口的协同控制时，通过引入一个新变量，即交叉路口（信号）j的相位差Oj，可以将此模型扩展到交通干道层。我们的目的是在总时间跨度T内，实现干道上所有车辆（车辆总数为N）的燃油消耗和行驶时间最小化，如等式（1）所示。FCn,t和TTn,t是车辆n在时间t的燃油消耗和行驶时间。参数mF和mT是货币值。例如，可以将mF设置为每升0.8美元（每加仑3美元），而mT为每小时12美元。在这里，我们应用Zhao等[24]开发的燃油消耗模型，如等式（2）所示。燃料消耗量FCn,t是基于车速vn,t计算的。如果车辆处于空转状态（速度小于8 km·h-1），则怠速状态指示变量In,t等于1，否则，指示变量In,t为0；如Zhao等[24]所述，燃油消耗参数a,b,c,d和e已经根据各种车辆类型进行校准。

为了协同多个交叉路口，我们需要在不同交通信号的协同相位之间建立连接，如每个交叉路口相位1（图2中的移动2和6）的绿灯开始时间。这些连接用两种类型的时间标记来表示：全局时间t和局部时间。全局时间t是指在协同操作期间每个信号都引用到的主时钟，其取值范围从零开始到总时间跨度T。局部时间指的是从零开始到周期时长C的局部交叉点j的时间。T和之间的关系如等式（3）所示：

式中，mod是指取模运算。相位差Oj是参考信号与信号j之间协同相位开始的时间差。等式（4）也描述了边界情况，其中，Omax表示最大相位差的参数。

为了进行信号协同，固定的周期时长约束是必需的。该约束要求相延续时间等于预定义周期时长C，如等式（5）所示。参数I和J代表研究范围内的周期和交叉路口总数。等式（6）表明了相延续时间的边界。当相交j处的周期i的相位持续时间为零时，跳过相k，这可以通过将最小绿灯时间设为零来实现。对于无法跳过的协同相，如相1（通过主干道的移动），最小绿灯时间应该设置为非零（如5 s）。等式（7）[或等式（8）]表明两个相中至少有一个等于零，因为两个相都包含冲突运动。相关内容可以在Li和Ban[17]的工作中找到。

为了计算交通网络中所有车联网的消耗，有必要知道每个互联车辆的信号状态，因为它会影响车辆轨迹。在等式（9a）中，如果信号在时间为红色，则信号状态（Sj,k,t）等于1，如果信号为绿色则等于零。变量表示在时间（即1,2,...,8）的有效相（绿灯）。等式（9b）在等式（9a）的基础上引入大M概念[25]。大M约束通常用基于二进制变量的值来限制变量的值，如等式（9b）中的二进制变量yt,1和yt,2。

在确认过每个时间点的每个交叉路口的信号状态之后，我们需要根据信号与车辆的相对位置找到距离车辆n前方最近的交通信号。等式（10a）使用指示变量yt,3和yt,4识别车辆n是否在交叉路口j的边界内：。等式（10b）在等式（10a）的基础上引入大M概念。每辆车都会在两个相位上有通行权。比如，相位1或相位2为绿灯时，由西向东的直行车辆拥有通行权。这种情况由等式（11）定义。是在时间t可以服务于车辆n的两个相位的最小信号状态，例如，如果其中一个相位为绿色（Sj,k,t=0），则Zn,t将为零。等式（12）确保只有在车辆进入交叉路口j的边界（在与交叉路口j的停车线之间）时，交通信号才会影响车辆的轨迹。

对于可在交叉路口j为车辆n服务的所有相k有

在确定了车辆n的信号状态之后，可以根据智能驾驶模型（IDM）估算和预测其轨迹[26]。考虑到信号状态对互联车辆的影响，我们将交通信号模拟为一个“虚拟车辆”，当信号状态为红色时，它是一个速度为零且位置预先确定的静止车辆。当信号为绿色时，它会从交通网络中消失。等式（13a）通过比较车辆n（dsignal,n）的最近前方交通信号的位置与车辆n（dn,t）和车辆n-1（dn-1,t）的位置，确定车辆n之前的车辆是真实车辆还是“虚拟车辆”。参数dsignal,n表示车辆n最近的前信号的位置。等式（13b）等价于式（13a）使用大M法。

等式（14）以及等式（15）更新了前车n-1的位置以及速度信息（vn-1,t是车辆n-1在时间t处的速度）。变量yn,t可以是真实的车辆或交通信号。

公式（16）～（19）应用了智能驾驶模型来计算车辆n在时刻t的加速度an,t。变量Sn,t表示对车距的估计，ln-1表示车长，Δvn,t表示车辆n与前车的速度之差，v0表示理想车速，Son表示静止车距，H表示理想车头时距，amax和bmax分别表示最大加速度和最大减速度。指数δ一般设为4。更多细节请参考Li和Ban等[17,23]的工作。

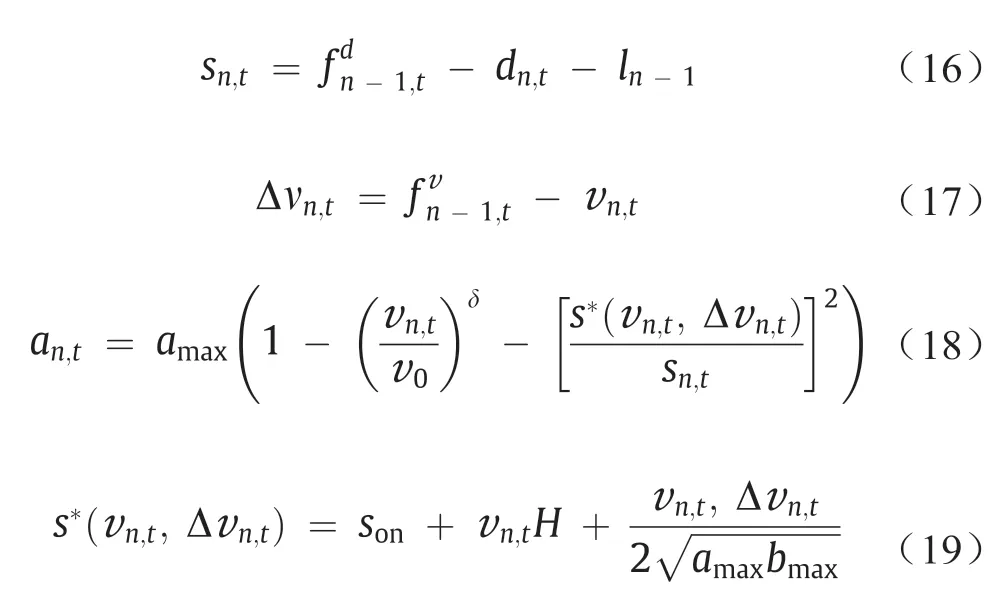
由IDM得到的加速度被用于预测车辆n的轨迹，如公式（20）、（21）所示。

公式（1）～（21）描述了车联网环境中多个交叉路口的信号优化和协同模型。当考虑每辆车的轨迹时，模型表明，该问题可以表述为MINLP问题。公式（1）～（21）是对参考文献[23]中的模型的重要扩展，但更为复杂。首先，变量的数量大大增加，从单交叉路口的八个相位变成八个相位乘以交叉路口数量，此外还新增了许多相位差变量。其次，道路干道或网络包含的车辆多于单个交叉路口。因此，预测车辆轨迹（即特定时间段和特定网络范围内的每辆车每秒的速度和位置）的计算量将会增加。此外，每辆车的状态与多个交通信号之间复杂的相互作用，导致模型需要许多if-then-else条件语句[公式（1）～（21）]。求解生成的MINLP公式更难，且求解过程不适用于实时信号控制。在下一节中，我们将介绍如何把基于车联网的交通信号优化和协同问题[公式（1）～（21）]分解为一个可以更有效地解决的分散式双层模型。

2.2.将信号协同过程重新构造为双层优化模型

由于MINLP公式[公式（1）～（21）]过于复杂，我们将该问题重新构造为分散的双层优化问题。在该双层优化模型中，我们没有将整个交叉路口的相位持续时间和偏移优化作为一个规划问题求解，而是将整个问题分解为两个级别：一个是交叉路口级别，即优化每个交叉路口的相位持续时间，一个是干道级别，即优化所有交叉路口的相位差。这种方法大大降低了原始数学模型的复杂性。

图3显示了双层优化模型的总体结构。假设所有交叉路口和车辆都已接入网络，并且它们可以相互发送消息。进一步假设已知一些初始相位差和相位持续时间。在这种情况下，本文使用著名的交通信号优化软件SYNCHRO 6计算得到了这些变量。然后，可以使用IDM来估算和预测出到达每个交叉路口的车辆。特别注意，此处使用包含两步法[23]的动态规划（DP）模型来计算每个交叉路口每个周期的最佳相位持续时间。该方法能够计算出满足单个交叉路口固定周期时长约束的相位持续时间。图4展示了DP方法的无环图，其等效于在图中找到最短路径。可变相位差指出了交叉路口和干道级别优化之间的联系。为了考虑相位差对单个交叉路口DP公式的影响，如公式（3）所示，我们使用交叉路口j的本地时间来实现和求解该DP问题。这从本质上将公式（1）～（21）定义的全干道模型缩减为针对每个交叉路口的模型。单个交叉路口DP算法的细节请参考[23]。

在干道上生成所有交叉路口的最佳信号计划几个周期后，这些数据会被传送到中央控制器，接着，在此处进行干道级别的相位差优化。通常，相位差值会被保留一段时间，并且不会每个周期都更新。在这里，我们假设相位差每隔特定个数的周期更新一次，即图3中的Nc。也就是说，Nc可能是10个周期。行驶超过Nc个周期后，交叉路口级别的优化终止，开启干道级别的优化。参数ε是决定干道级别计算是否收敛的阈值，一个可能的取值是0.01。在本节中，我们进一步将偏移优化问题重新表示为MINLP，但变量要少得多，因为每个交叉路口的相位持续时间可以通过解决上述交叉路口级别模型而获得（使用参考文献[23]中的DP方法）。干道级别优化的目的是最大限度地减少干道主要街道上所有联网车辆的油耗和行驶时间：

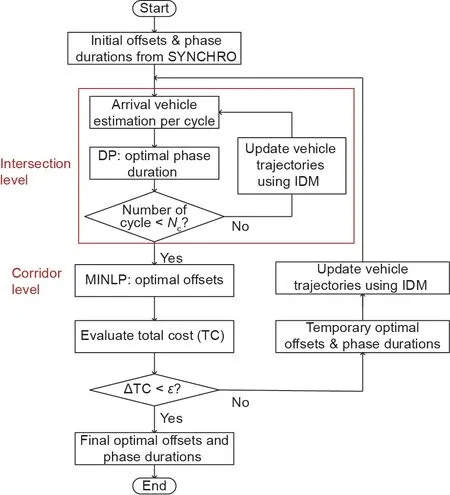
图3.交通信号双层优化模型的解决方案。Nc：周期数；ε：决定干道级别计算是否收敛的阈值。

图4.DP方法的无环图。xp*表示分配给阶段p的最优绿灯时长；sp是状态变量，代表从开始到结束的总时长。带虚线的箭头表示DP中的阶段处理序列。

式中，N是主要道路上联网车辆的总数。该双层优化模型的目标与公式（1）代表的MINLP问题不同，因为在双层优化模型中，只考虑了主要街道上车辆的协同问题。按照协同控制信号灯行驶的联网车辆会实现成本最小化。双层优化模型中关于相位差的约束与公式（3）和公式（4）一致。

由于最佳相位持续时间是根据交叉路口级别的模型生成，原始MINLP模型[公式（1）～（21）]中的变量对应了干道级别模型中的。信号状态可由公式（23）估算。

信号状态确认之后，可以用公式（10）～（21）和IDM预测出车辆的轨迹。综上，公式（10）～（23）建立了一个干道级别的相位差优化模型。该模型同时也是一个MINLP问题，但是比原始MINLP问题[公式（1）～（21）]的维度简单许多。原始MINLP模型中的相位持续时间在干道级别相位差优化模型中不再是变量，因为已经在交叉路口级别模型中使用动态规划对它们进行了优化。该干道级别模型可以用Matlab中的NOMAD求解器求解[27]。该模型使用IDM计算/更新车辆随时间变化的速度和位置。如图3所示，为了找到最优相位差，需要对干道级别MINLP模型生成的“临时”最优偏移进行迭代计算，直到总成本收敛为止。收敛的标准是两次连续迭代中估算的总成本之差（即ΔTC）小于阈值，如10-5。

3.数值实验

本文提出的交通信号优化和协同控制模型及解决方法在仿真网络中进行了测试，网络干道包含了五个信号交叉路口。两个相邻交叉路口相距800 m（0.5 mi）。WB和EB是协同控制方向。如图5所示，交叉路口的边界被定义为停靠线上游400 m和下游400 m之内。在整个网络的边界处生成随机到达的车辆，其到达时间、初始速度和转向都是已知的。我们还假设进场时只有一个车道（加上交叉路口的左转弯车道），因此没有模拟变道行为。联网车辆的渗透率假定为100%。评估提出的方法及将其性能与其他模型进行比较共分成三个步骤。首先，在不同的交通需求水平下，在SYNCHRO中计算最佳信号时序参数，包括周期时长、相位持续时间和相位差。其次，针对每种情况，采用不同的方法来计算最佳信号计划（相位持续时间和相位差）。最后，通过在同一仿真网络中实现上述计算方法，来比较各个方法的性能。请注意，SYNCHRO在某一特定时间段内实施了固定的最佳信号方案（基于平均交通需求），该方案不考虑单个车辆的轨迹或不同类型的车辆。相反，利用CV技术，在信号时序确定过程中，提出的双层优化模型考虑了实时到达的车辆轨迹、变化的车辆类型以及转弯/通过车辆的数量。

我们首先测试了六个案例，这些案例考虑了不同的交通需求水平和车辆类型（表1），与Li和Ban[17,23]的测试类似。在案例I～III中，所有车辆均为轿车。主要街道东西（WE）方向的需求设置从低[每小时250辆车（vph）]到高（800 vph）。对于次要街道的南北（NS）方向，需求设置为125 vph、250 vph和250 vph。在案例IV～VI中，车辆需求水平与案例I～III中相同，而车辆类型不同。南北方向上的所有车辆均为电动汽车（EV），WE方向上的所有车辆均为公共汽车。在这六种情况下，80%的互联车辆将为直行车辆，而其他20%的互联车辆将会在每个交叉路口左转。

表2显示了在十个周期中使用三种方法生成的不同信号配时的总成本（突出显示了每个案例的最低总成本）。第一种方法是SYNCHRO软件中的触发式信号灯控制系统。给定干道的地理信息和每个方形的车流量，SYNCHRO可以计算出最优信号参数，包括相位持续时间、周期时长和相位差。最优信号计划，连同随机生成的到达车辆和使用IDM得到的车辆轨迹，都在仿真网络中实现，以计算总成本，即公式（1）和公式（2）。表2中MINLP方法和双层优化模型方法也遵循相同的程序来计算成本。注意，为了进行信号协同控制，我们在本研究中使用了固定的周期时长约束。使用SYNCHRO估算不同情况的周期时长，即低流量需求（案例I和IV）为60 s，中等流量需求（案例II和V）为80 s，高流量需求（案例III和VI）为120 s。第二种方法，即公式（1）～（21）所表示的MINLP，用Matlab中的NOMAD求解器求解。如图2所示，每个信号有8个相位。如果每10个周期计算一次信号计划，则对于包含5个信号的仿真网络来说，将有40个表示相位持续时间的变量和4个相位差变量。第三种方法是本文提出的双层优化模型，可以通过基于预测的方法求解。在交叉路口级别，用DP方法求解每个交叉路口的相位持续时间，并且可以在每个周期更新。在干道级别，每10个周期求解一次偏移。

对于所有案例，MINLP和双层优化模型的结果都比SYNCHRO的结果要好。对于案例III和案例IV，双层优化模型的结果要优于MINLP的结果。图6显示了每个案例中模型性能的提高程度。在需求水平相对较低的案例I和IV中，改进幅度小于其他案例；这一发现可能表明，在流量相对较小的情况下，协同控制带来的收益有限。

图5.包含五个交叉路口的仿真网络。WE：东西方向边界（协同控制后的方向）。

表1 不同交通需求等级和车辆类型下的六个案例

除了行驶时间和燃料消耗的成本外，我们还比较了所有方法中的停止次数，如表3和表4所示。在所有六个案例中，协同控制方向的停车次数通常少于其他方向的停车次数。此外，SYNCHRO方法下的停车次数大于从MINLP和双层优化模型计算出的停车次数。

为了进一步评估协同控制是否可以使整个网络（包括不同情况下的主要街道和次要街道）受益，我们比较了两种情况下模型性能的改进：有协同和无协同（即相位差等于零）。例如，在MINLP中，我们首先求解仅包含40个相位持续时间变量的模型，并将所有相位差设置为零。然后，我们在IDM中实施估算的信号计划，并分别估算主要街道和次要街道的总成本。将这一成本与求解整个模型[公式（1）～（21），优化了相位持续时长和相位差]的结果进行比较。双层优化模型采用同样的流程。表5展示了比较结果。负值在表中加粗显示，表示进行协同控制后主干道或次干道的路网表现反而变差。如果对主干道进行协同控制，那么在低交通流量（案例I或案例IV）下，MINLP和双层优化模型均表现不佳，而在较高交通流量水平（案例II、III、V和VI）下模型的改善更为显著。结果表明，协同控制方案对交通流量低且车辆随机到达的干道作用不大，因为这些车辆不太可能形成受相邻交叉路口影响较大的车队。对于次要道路，无论是正面还是负面的影响都相对较小。在这六个案例中，主干道协同对次要街道上的车辆几乎没有影响。

表2 六个案例各自的总成本（单位：美元）

图6.案例I～VI中模型性能的提升（对比SYNCHRO）。

表3 协同控制方向的停车次数

表4 所有方向的停车次数

表5 协同控制后针对主要街道和次要街道的模型性能改善情况

这六个案例测试了交通流量和车辆类型的各种组合对信号协同控制算法的影响。本文提出的方法仍需在相反方向车流量不同的场景下进行测试。因此，将测试另外三个案例（案例VII～IX）。首先，向仿真网络中添加了向右转的交通需求。在案例VII～IX中，从每种方法总需求的10%～20%之间随机抽样车辆执行左转和右转。另外，相反方向的交通需求也不相同。例如，在主要街道上，E-W和W-E方向的流量不同。对于案例VII和VIII，每个方向的交通需求是给定值，如表6所示。在案例IX中，每个方向的交通需求在一定范围内随机采样。例如，在E-W方向上，初始需求是从250 vph至500 vph范围内随机（均匀）选择的。在所有案例中，MINLP和双层优化模型的性能均优于基线SYNCHRO模型。模型改进如图7所示。

图8显示了在4000 m干道内使用不同信号计划更新10个周期（600 s）后的车辆轨迹。车辆在图5中沿W-E方向行驶。与图8（a）中使用SYNCHRO生成的轨迹相比，图8（b）和（c）中使用MINLP方法和双层优化模型的延迟和停车次数明显下降。通过优化信号计划，车队随机生成的车辆可以顺利通过交叉路口。

表6 不同交通需求水平及相反方向下，不同方法的总成本

图7.案例VII～IX中模型性能的提升（对比SYNCHRO）。

图8.不同信号计划生成的车辆轨迹。（a）使用SYNCHRO的信号计划；（b）使用MINLP的信号计划；（c）使用双层优化模型的信号计划。

图9.案例I中双层优化模型的收敛情况。（a）每5个周期更新一次相位差；（b）每10个周期更新一次相位差。

本数值实验测试了不同方法在10个周期时的表现（每个周期时长固定，总时间为10～20 min）。可以延长仿真周期，但这样做明显需要更长的计算时间。当车辆需求水平较高，信号计划更新间隔较小（意味着变量更多）时，NOMAD求解器可能无法找到可行的解决方案。双层优化模型通常可以确保收敛，但是计算时间会根据上述因素而有所不同。图9显示了案例I中相位差更新间隔不同时的迭代次数。程序通常会在10次迭代内收敛。在其他案例中也可以找到类似的模式，在此省略。

4.结论

本研究开发了一个信号时序优化和协同控制的模型，该模型在CV环境中考虑了单个车辆的轨迹。首先提出了集中化方案MINLP，规定信号灯周期时长为孤星时长，以便做多个交叉路口相位差优化。假设交通路网中联网车辆市场占有率为100%，本文提出的方法先用IDM跟车模型来估计和预测车辆的轨迹。由于模型过于复杂，我们将问题整理成双层优化模型：底层是交叉路口级别，使用笔者先前为每个交叉路口开发的DP方法，生成最佳相位时长，上层是干道级别，为所有交叉路口更新最佳相位差。双层模型降低了MINLP的复杂性。为了解决该模型，我们进一步开发了一种基于预测的求解方案，可以迭代地解决该问题。通过交通仿真，我们在包含五个路口的干道中测试了所提出的模型和求解方法。MINLP和双层模型的结果在交通延误和燃料消耗方面均优于SYNCHRO生成的信号灯优化方案。仿真中对不同交通量和车辆类型的多个情景进行了测试。结果还表明，信号协同控制对交通流量低的交叉路口和次要道路上的车辆带来的改善有限。在以后的研究中，我们将放宽联网车辆市场占有率为100%的假设，这需要我们基于采样的CV轨迹对非CV的轨迹进行估计。此外，我们计划使用更多数据（如实际流量和信号时序数据）测试和验证所提出的双层优化方法。

致谢

作者要感谢两位匿名审稿人的深刻见解，他们帮助改进了本文的原始版本。这项研究得到了纽约大学互联城市智慧交通（C2SMART）一级大学交通中心[由美国交通部（USDOT）资助]的部分支持，该资助来自华盛顿大学（69A3551747124）。

Compliance with ethics guidelines

Wan Li and Xuegang Ban declare that they have no conflict of interest or financial conflicts to disclose.