小周期区域内热-力-电耦合问题的高阶双尺度渐近分析

陈惠敏, 冯永平

(广州大学 数学与信息科学学院, 广东 广州 510006)

0 引 言

随着热压电材料在生活中的广泛应用,人们对此类材料的热-力-电行为也产生了浓厚的兴趣.早在1974年,Midnlin[1]就第一次提出了热-力-电的三维线性控制方程,并分析了解的一些属性；Nowacki[2]给出了有关热压电材料的一般理论和数学模型,这些结论已经被各种数值方法当做基础进行分析与验证.基于上述已得到的理论,Ashida等[3]运用势函数方法求解了热压电材料的三维轴对称问题.由于材料的复杂性,这类结构一般具有某种小周期性,但对小周期区域内新型热电材料导效性能研究的文献甚少.本文基于上述理论,利用双尺度方法探讨具有小周期结构的热-力-电耦合问题的双尺度渐近解.

目前,利用双尺度方法解决小周期区域内具有震荡系数的数学问题已有了越来越广泛的应用.文献[4]利用双尺度方法分析具有小周期条件热弹性耦合问题的二维线性控制方程；文献[5]主要利用双尺度方法对具有小周期孔洞结构区域中的压电耦合问题分析了均匀化力学、介电常数的正则性；宋士仓和王自强等[6-7]利用双尺度方法探讨稳态和非稳态条件下小周期复合材料的热传导问题,得到具有震荡系数的抛物型方程的渐近展开式,并分析其收敛性;文献[8]利用双尺度方法解决小周期孔洞区域中带阻尼项椭圆方程；文献[9]利用双尺度方法研究了一类化-力耦合问题等.

由于热压电材料局部分布的不同,结构并不是绝对均匀化分布的,存在多尺度的跨度与效应问题,并且因为材料局部具有很强的震荡性,数学上要得到热-力-电耦合问题的精确解是比较困难的.因此,利用双尺度方法讨论其近似解有一定的可行性,本文主要研究具有小周期结构、并且满足狄利克雷边界条件的热-力-电耦合问题.数学上,周期性区域中的热-力-电耦合问题可由以下偏微分方程边值问题表述[10].

(1)

其中：

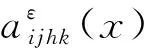
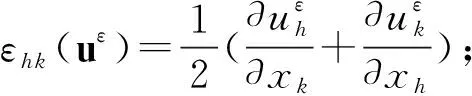
(3)Ω是满足Lipschitz边界条件的有界周期闭区域；

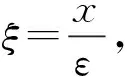
考虑如下的偏微分方程组[4]：

(2)

注1 当aijhk(ξ),kij(ξ)满足一致椭圆条件与正定条件时,易证上述问题存在唯一解(相差一个常数),即

其中,{ηih}是任意实对称矩阵,1,2是与ε无关且大于0的常数.

同样地,元素kij(ξ)是有界可测函数,并满足：

其中,{ηi}是任意实向量,1,2是与ε无关且大于0的常数.

本文利用文献[4-5]等相关定理与方法得到此条件下该方程的均匀化方程和均匀化常数,并讨论高阶双尺度近似解与二阶双尺度近似解的误差估计.

将方程组(1)转换成以下两个方程组：

(3)

(4)

1 Τε(x),uε(x),φε(x)的双尺度渐近展开

首先探讨Τε(x),uε(x),φε(x)如下的形式渐近展开式：

(5)

(6)

(7)

将式(5)代入方程(3)中,通过计算、整理,比较两端ε的同次幂系数,分析ε-1的对应系数,可以得到：

(8)

Q是小周期单胞区域.

比较等式两边关于ε0的对应系数,可以得到：

上面等式两边在Q上关于ξ作积分,得到：

因此,T0(x)为方程组(3)的均匀化解,由下面的方程定解：

(9)

(10)

由关于ε0的对应系数可知标量函数Hα1α2(ξ)可通过下面单胞问题定解：

(11)

比较等式两边关于ε1的对应系数,可以得到如下确定单胞函数的方程：

(12)

注3 上式(8)、(11)和(12)中边界条件也可以利用周期边界条件,当小周期系数满足某种对称性时,可证明不同边界定义的周期单胞函数仅相差一个常数.

类似地,将式(5)、(6)和(7)代入方程组(4)中,通过计算、整理,比较两端ε的同次幂系数,分析ε-1的对应系数,可以得到如下几个确定单胞函数的方程组：

(13)

(14)

(15)

比较等式两边关于ε0的对应系数,可以得到：

eα1mα2(ξ)+eα2jk(ξ)εjk(Mα1m(ξ))-

上面等式两边在Q上关于ξ作积分,得到：

因此,u0(x)和φ0(x)是方程组(4)的均匀化解,其由下面的方程组定解：

(16)

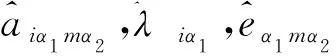
(17)

(Eα1α2m(ξ),Mα1α2m(ξ)),(Fα1α2(ξ),Nα1α2(ξ))和(Gα1(ξ),Pα1(ξ))可分别通过下面单胞问题定解：

(18)

(19)

(20)

比较等式两边关于ε1的对应系数,可以得到如下几个确定单胞函数的方程组：

(21)

(22)

(23)

注4 由Korn不等式及Lax-Milgram引理可知方程组 (13)、(14)、(15)、(18)、(19)、(20)、(21)、(22)和(23)存在唯一弱解.

综上,有下面定理.

定理1 假设f,ρ,g,u0,T0,φ0在Ω内足够光滑,则

(i)方程组(1)有(5)、(6)和(7)的形式渐近展开式;

(ii)当 <α>=1时，单胞函数Hα1(ξ),(Eα1m(ξ),Mα1m(ξ)),(Fα1(ξ),Nα1(ξ)),(G0(ξ),P0(ξ))分别由式(8)、(13)、(14)和(15)定解;

(iii)均匀化解T0,(u0,φ0)分别由式(9)、(16)定解;

(v)当 <α>=2时，单胞函数Hα1α2(ξ),(Eα1α2m(ξ),Mα1α2m(ξ)),(Fα1α2(ξ),Nα1α2(ξ)),(Gα1(ξ),Pα1(ξ))分别由式(11)、(18)、(19)和(20)定解;

(vi)当 <α>=3时,单胞函数Hα1α2α3(ξ),(Eα1α2α3m(ξ),Mα1α2α3m(ξ)),(Fα1α2α3(ξ),Nα1α2α3(ξ)),(Gα1α2(ξ),Pα1α2(ξ))分别由式(12)、(21)、(22)和(23)定解.

2 渐近误差估计

在实际计算中,通常运用下面的近似计算公式.

o(ε2),x∈Ω,

对以上二阶近似解,有下面的渐近误差估计.

定理2 设Tε(x)是方程(3)的弱解,假设T0(x)∈H4(Ω),ρ(x)∈H2(Ω),那么有

其中,C是与ε、T0(x)和ρ(x)无关的正常数.

定理3 设uε(x)、φε(x)和Tε(x)是方程组(4)的弱解,假设u0(x)∈H4(Ω)，φ0(x)∈H4(Ω)，T0(x)∈H4(Ω),ρ(x)∈H2(Ω),f(x)∈H2(Ω),g(x)∈H2(Ω),那么有

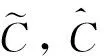
注5 上述两个定理可以运用变分方法与偏微分方程的正则性理论给出证明,限于篇幅限制,其证明过程另文讨论.

3 小 结

在实际问题中,想得到此类热-力-电耦合问题的解析解是很困难的,因此,只能通过近似解去逼近它.本文主要研究此类问题的双尺度渐近分析,给出了方程中Tε,uε和φε的双尺度渐近展开式,从而得出方程的均匀化解和均匀化方程.基于构造的高阶双尺度渐近展开式,分析了二阶双尺度渐近解的误差,改进了已有结果,为进一步进行数值模拟提供了理论基础.

对其他更一般区域内的热-力-电耦合问题，可以利用相似的双尺度匹配边界层的方法进行方程解的渐近性能分析.