EMFedAvg
——基于EMD距离的联邦平均算法
周旭华, 丛 悦, 李鉴明, 仇计清
(1. 移动互联网系统与应用安全国家工程实验室,上海 201315; 2.广州大学 网络空间安全先进技术研究院,广东 广州 510006; 3.河北科技大学 理学院,河北 石家庄 050027)
当今时代,信息技术给人们工作和生活带来极大便利的同时,日益渗透到人们生活的方方面面.个人信息一旦被泄露,人们的日常生活将会受到严重的干扰.据“中国网络安全审查技术与认证中心”统计,2020上半年全球共发生20起重大数据泄露事件,其中8起发生在国内[1].与之相对应,公众对个人隐私[2]的保护意识逐渐提高,法律法规对用户隐私的监管越来越严格[3-6],如《中华人民共和国民法典》、欧盟的《通用数据保护条例》[7]等.因此,数据的使用越来越受到限制.
与之矛盾的是,机器学习和人工智能技术能够取得如今的成就,很大程度上得益于当今互联网时代的海量数据.然而法律监管、商业竞争、隐私安全[8]等因素使得数据以孤岛的形式存在[9-10],难以发挥其应有的价值.
因此,设计一种能解决数据孤岛与数据利用矛盾、安全高效的机器学习框架具有重要的研究意义与价值.
联邦学习是一种能解决数据孤岛问题且满足隐私保护和数据安全要求的可行方案.与现有机器学习方法一样,联邦学习要面临的首先是数据问题.现有的机器学习任务默认训练数据遵循独立同分布(Identically Independently Distributions,IID),神经网络、深度学习等常见算法一般都将数据遵循IID 的假设作为其推导的一部分.然而真实世界中数据相关性无处不在,非同源数据常常具有不同的概率分布,而联邦学习往往面临着非独立同分布(non-IID)[11-12]的数据.在一些场景中,直接应用已有的机器学习算法基于non-IID数据进行模型训练[13],由于算法本身的先进性,训练结果仍然较好.但在很多情况下,利用现有的机器学习算法和框架,基于non-IID 数据训练会出现意想不到的负面效果,比如模型准确度低[14]、模型无法收敛等[15].
联邦平均算法(Federated Averaging,FedAvg)[13]是联邦学习中第一个提出的解决non-IID问题的算法,使得联邦学习中各参与方可以协同训练卷积神经网络,其有效性在分类算法的典型数据集MNIST[16]、CIFAR-10[17]和莎士比亚文本数据集[18]均得到验证.在FedAvg基础上,Zhao等[14]提出数据共享策略,各参与方仅共享5%的数据作为可以公共使用的数据子集,就能使FedAvg算法在non-IID划分的CIFAR-10上提升30%的准确率.本文在手写数字集MNIST上进行实验,计算non-IID划分MNIST数据子集的EMD距离,并从小到大排序,以第三四分位数为分界线,去掉EMD值较大的后1/4的参与方,及时淘汰不良参与方[19-20],留下优质参与方进行后续训练,在解决数据量偏差与特征分布偏差上取得了较好的效果,100轮迭代后联邦平均算法FedAvg在non-IID问题上的准确率提升了5%.主要表现在:
(1)准确率提升.针对non-IID的数据问题,FedAvg算法准确率一般在85%~86%之间.本文在FedAvg的基础上结合了EMD距离,在权重更新的时候,及时去掉分布差异过大的参与方,最终使FedAvg在non-IID的数据准确率提高到了91%.
(2)通信成本降低.与Zhao等[14]不同,本文提出的方法没有采用数据共享策略,减少了联邦训练过程的通信次数和数据通信量,节约了网络通信成本,提高了联邦训练的效率.同时,不共享任何数据可以使各方数据隐私得到更好的保护.
(3)为各方贡献提供度量参考.MNIST数据集经过non-IID划分后并不是所有的数据子集都适合加入到联邦学习中来.实验发现,去掉数据分布差异过大,即EMD距离后1/4的数据子集,淘汰不良参与方,FedAvg的准确率有了明显的提升.由此可以衡量各方贡献的大小,从而建立一个更加有效的效果激励机制.
1 相关概念
1.1 联邦学习
为了打破数据孤岛和行业壁垒,谷歌首先提出了联邦学习的概念[13,21-23],并应用到了安卓手机输入法的预测.中国计算机学会(China Computer Federation,CCF)把联邦学习定义为一种加密的分布式机器学习,分布式的各参与方数据不出本地,利用加密的中间结果,如差分隐私[24-26]、同态加密[27-29]等进行协同训练一个优于各方独自训练的全局模型,且无法从中间结果反推各参与方的数据.
联邦学习让每一个参与方利用己方数据在本地训练同一个机器学习模型,训练完成后,让各参与方在各自训练模型上利用参数进行交流沟通,最后通过模型聚合方法,经过一系列迭代计算,获得一个最终的全局模型.按照Yang等[30]的定义,设有N个参与方{F1,…FN},各参与方拥有的数据为{D1,…DN},传统做法是把N个参与方拥有的数据收集起来得到一个整体的数据集D=D1∪…∪DN,并用D训练得到一个整体的模型MSUM.联邦学习是各参与方协同训练得到一个全局最优模型MFED.设MSUM的准确率为VSUM,MFED的准确率为VFED,δ为无穷小的非负实数,联邦学习追求的效果为
VFED-VSUM<δ,
即联邦学习模型在准确率上无限接近传统模型.联邦学习架构如图1所示.

图1 联邦学习架构Fig.1 Federated learning structure
联邦学习在诸多领域拥有广阔的研究价值和应用前景,众多与金融[31]、医疗[32]、智慧城市[33-34]、物联网[22]和区块链[35]等领域结合的研究都取得了一定的进展与成就.
1.2 数据非独立同分布(non-IID)
虽然IID的概念在现有机器学习方法中已经比较明确[36],但现实生活中non-IID的数据更为普遍[37],以谷歌安卓手机输入法预测GBoard[38]为例,不同个体、不同地理位置、不同时间(如昼夜)等因素,输入法里常用词频率分布往往不同,甚至对于不同文化背景的人,同一个词的含义也不一样.因此,相比于传统机器学习中单一场景的IID数据集,联邦学习考虑的通常是各参与方之间非均匀、非独立同分布的non-IID数据[39-40].
Kairouz等[41]把联邦学习中非独立同分布数据分为五种情况:①特征分布偏差,对于同一个特征其边缘分布不同,如手写同一个数字,不同的人书写的笔迹宽度和力度一般不一样;②标签分布偏差,表现为特定的标签和特定的群体绑定,如写汉字的基本上是中国人;③同样的标签不同的特征,如都是好评但评价电影和评价食品的词不一样;④同样的特征不同的标签,如同一个词对于不同文化背景的人感情色彩可能不同;⑤各参与方的数据量偏差.由此可见,寻找处理非均匀、非独立同分布数据算法在联邦学习的研究中至关重要.
现实世界中,联邦学习数据集可能包含上述五种数据偏差的组合,然而如何处理参与方之间的数据偏差是一个重要的开放问题.大多数关于non-IID数据的工作主要关注标签分布偏差,其non-IID数据集一般由标签的扁平数据划分而来.更准确地理解现实世界non-IID数据的本质,有利于构建可控且真实的non-IID数据集,以便测试算法性能,并评估它们对不同程度偏差异构数据的鲁棒性.
此外,由于联邦学习是加密的分布式训练,不同于传统的分布式机器学习,联邦学习过程中网络通信的消耗往往比计算消耗大.除了数据non-IID,联邦学习还要考虑带宽、参与方设备可用性,以及数据通信量等问题.
1.3 EMD距离
EMD距离是基于概率分布的度量距离[42],是一种评价特征空间中两个多维分布之间相似度的方法,常用于图像检索中图片相似度的度量.一般来说,图像的特征很多,其分布可以用一组集群表示,其中每个集群均由其平均值以及属于该集群的分布百分比,即权重来表示,这种表示称为图像特征分布的签名(Signature).设s是一个签名,m是某个特征,w是该特征的权重,则签名可以写作s=(m,w).不同签名可以有大小不同,如表示简单分布的签名比表示复杂分布的签名要短.
设P={(p1,wp1),…,(pm,wpm)}为具有m个集群的签名,Q={(q1,wq1),…,(qn,wqn)}为具有n个集群的签名,D=[dij]为单个特征之间的距离,每一项dij表示pi与qj的距离,因此,D是一个M*N的矩阵.对于P和Q,设流矩阵为F=[fij],其中每一项fij表示从pi到qj的流数目,则EMD距离可以进一步转化为线性规划问题,即找到矩阵F中的一个流,使得从P到Q的全局代价最小,公式如下:
且服从以下四个约束条件:
fij≥0,1≤i≤m,1≤j≤n
(1)
(2)
(3)
(4)
其中,式(1)约束流是从P流向Q而不是反过来.式(4)是尽可能地减少流动的距离.因此,两个不同分布P与Q的EMD距离为
实际应用中使用EMD距离时,不同情况使用方式可能不同,所选取的特征只需符合以上四个约束条件即可.
2 相关工作
本节主要介绍与本文相关的已有算法,主要是联邦平均算法FedAvg、基于损失的自适应增强联邦学习,以及联邦效果激励机制等.
2.1 FedAvg

fi(w)=l(xi,yi;w)为模型参数w对个例(xi,yi)进行预测的损失.对于第k个参与方
则联邦模型总体损失函数为
第k个参与方的梯度为gk=▽Fk(wt),学习率为η,则第t轮迭代得到的新参数为
每个参与方的本地更新为
FedAvg的全部伪代码如算法1所示.
算法1 FedAvg,K是参与者总数
服务器:
初始化w0
对每一轮t=1,2,…:
m=max(C*K, 1)
随机选取参与者子集St
St全体并行计算:

客户端:
把nk分成大小为B的块
对本地1到E轮迭代:
对每一块:
w←w-η▽l(w;b)
返回w到服务器
McMahan等[13]的实验结果表明,该算法对IID数据和non-IID数据均具有良好的鲁棒性.
2.2 算法优化
在联邦学习框架中,通过算法优化可以提升各参与方之间参数更新的通信效率.在non-IID情况下,Woodworth等[43]通过设计一个间歇性通信模型,其中无状态参与方参与全部T轮中的每一轮,在每一轮中,每个参与方可以计算其中部分样本的梯度,再同步地将参数传递给所有其他参与方.在这种场景中,相对于通信成本,本地计算量很大.
在FedAvg算法的基础上,Li等[44]设计了一种FedProx算法.该算法的关键思想是系统异质性和统计异质性之间存在相互作用.由于系统约束而简单地删除网络中的离散者可能会隐式地增加统计异质性,因此,该算法在FedAvg的基础上做了一个小修改,允许基于底层系统约束跨设备执行部分工作,并安全地合并起来.理论上,FedProx使用不同度量来捕获网络中的统计异质性,并在有限设备不同假设下为凸函数和非凸函数提供收敛保证.收敛分析还包括每个设备在本地执行可变数量工作的设置.
2.3 数据共享策略
对于联邦学习non-IID的情况,可以适当添加数据以使参与方之间的数据分布更加相似.一种可行方法是创建一个可以在全局共享的小型数据集,即数据共享.该数据集可能来源于一个公开可用的代理数据源,可能来源于一个不涉及隐私的客户数据的单独数据集,也可能来源于原始数据的精馏[45].
对于用高度不均匀的non-IID数据来训练的神经网络,联邦学习的准确性显著降低,当每个参与方只训练己方单一类的数据时,最高可降低约55%[14].这种精度降低可以用权重发散来解释,而权重发散可以通过每个参与方数据分布的EMD距离来量化.当EMD超过一定阈值时,联邦学习的精度会急剧下降.因此,对于高度不均匀的non-IID数据,可以通过数据共享缩小各参与方数据集的EMD距离,以提高模型准确率.
2.4 LoAdaBoost FedAvg算法
FedAvg为处理联邦学习提供了一个范例和解决方案,Zhao等[14]指出,由于non-IID的数据分布场景下SGD不再是数据全体的无偏估计,FedAvg在non-IID划分的MNIST数据集上最大的精度损失达到了11.31%.为此,Zhao提出了数据共享策略以提高FedAvg在non-IID的准确率.为处理大规模、高敏感性的数据,Huang等[46]结合数据共享策略,提出了自适应[47]数据增强的LoAdaBoost FedAvg算法,该算法迭代的参考指标主要是全局损失函数的中位数.

2.5 效果激励机制
不同于现有的机器学习方案,联邦学习系统中各参与方有较大的自主权,联邦建模需要各参与方的积极参与.因此,联邦学习有必要建立一个兼顾公平与效率的效果激励机制(Federated Learning Incentivizer, FLI)[48]才能维持联邦学习的长期稳定,从而吸引更多的个人或机构参与到联邦学习中来.
参与方加入到联邦学习,共同构建一个机器学习模型,模型带来的收益可以用收益分享博弈[49]来划分.收益分享博弈主要分为平均分配、边际收益和边际损失三类.通常,一轮联邦迭代t会产生该轮迭代的收益,设一个参与方i在第t轮迭代从总预算B(t)中得到的分享收益为
其中,ui(t)表示参与方i对收益B(t)产生的效用,其数值要根据收益及分配方法计算.
此外,基于边际收益的常用方法有工会博弈收益(The labour union game profit-sharing)[50]、沙普利博弈收益分享(The Shapley game profit-sharing)[51]等.设v(F)为评估联邦集合体F效用的函数,工会博弈收益分享方法以各参与方加入联邦集合体F的相同顺序计算其边际收益:
ui(t)=v(F∪{i})-v(F),
不同于工会博弈收益分享,沙普利博弈收益分享排除了参与方加入顺序不同的影响,从而更加公平地评估各参与方对联邦集合体的边际贡献.该方法把联邦集合体分为m个部分(P1,P2,…,Pm),每个参与方以不同顺序加入联邦所产生的平均边际贡献为
[v(P∪{i})-v(P)].
基于边际损失的方法主要考虑参与方离开集合体时带来的收益影响,公平价值博弈方法(The fair-value game)[43]是一种基于边际损失的方法,其参与方收益计算如下:
ui(t)=v(F)-v(F{i}).
在本文提出的EMFedAvg算法中,ui(t)可以通过各参与方的EMD距离来定量计算,相比上述方法,EMFedAvg提供了准确计算参与方贡献ui(t)的方案,使得联邦建模的收益分配更加公平、客观.
3 EMFedAvg
数据共享策略可以在一定程度上缓解non-IID的情况,但有泄露数据的风险,同时也增加了中央服务器和各参与方的通信负担,现实情况也不存在数据共享这种理想情况,而FedAvg算法在non-IID数据上的效果还有待提升.为了解决这个问题,本文提出了基于EMD距离的联邦平均算法EMFedAvg,针对non-IID的情况,在没有数据共享的条件下,把FedAvg的准确率提高到了91%,首次把FedAvg在non-IID场景下的准确率提高到90%以上.
3.1 数据集划分
为模仿真实场景中non-IID的数据分布,实验用标签0~9按从小到大的顺序对MNIST训练集60 000张手写数字图片进行排序,排完序后,再把训练集依次划分为200片,每片包含300张图片.经过划分,每一片里包含的图像都是同一个数字.把200片训练数据分发给100个参与方,每个参与方分到的训练数据集只有两种可能:只包含一个数字的600张图片和包含两个数字各300张图片.训练全程没有数据共享,各参与方只能接触到分配给己方的数据,且最多只能接触到两个不同的数字.因此,各参与方的数据种类和对应种类的图片数目都有不一样的可能,是一种non-IID划分的方法,如图2所示.

图2 200*300 non-IID划分MNISTFig.2 200*300 non-IID split of MNIST
3.2 权重更新与异常处理
对比FedAvg算法,训练开始的时候对权重w0进行随机初始化.对于联邦整体的每一轮迭代,迭代完都会用每个参与方样本的权重分布与整体权重分布计算一个EMD值,并对EMD值由小到大排序,排在EMD值第三四分位数后面的参与方认为与总体分布差异过大,会降低联邦模型效果而被淘汰.设第t轮被淘汰的参与方数目为qt,剩下来的参与方集合为Pk,则第t轮没被淘汰的参与方k损失函数为
其中,fi(w)=l(xi,yi;w),与FedAvg算法里含义相同,为本地模型参数w对数据实例(xi,yi)的预测损失.由此得到第t轮联邦模型总体损失为
同样设第k个参与方的梯度为gk=▽Fk(wt),学习率为η,则第t轮迭代得到的新参数为
总结起来,EMFedAvg算法的伪代码如算法2所示.
算法2 EMFedAvg
服务器:
随机初始化w0
对每一轮t=1,2,…:
更新全局权重wt
计算参与迭代的参与方权重的EMD距离
淘汰EMD距离大于第三四分位点的参与方
Pk全体并行计算:
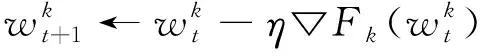
参与方:
对本地1到E轮迭代:
对每一片:
w←w-η▽l(w)
返回w到服务器
3.3 计算EMD距离
针对3.1中的数据集划分,联邦学习中各参与方的数据分布和总体数据分布的差异,即权重偏移可以用以下公式计算:
w_d=‖wFedAvg-wSGD‖/‖wSGD‖.
Zhao等[14]证明权重偏移可以通过EMD距离来进行度量,p(y=i)为样本标签总体的概率分布,pk(y=i)为第k个参与方的样本标签概率分布,则从参与方k到联邦总体分布的EMD距离为
其示意图如图3所示.
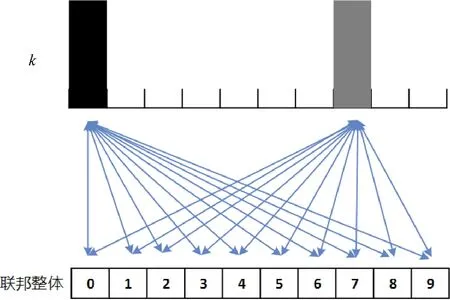
图3 EMD距离示意图Fig.3 EMD sketch map
算出EMD距离后,各参与方对联邦整体的贡献值就可以借助EMD值来定量计算了.这里给出一个参考,即每个参与方在第t轮迭代产生的贡献ui(t)为
其中,α为可调整的参数,b为偏置项.
3.4 训练流程
EMFedAvg采用的是经典的联邦学习架构,整体流程如图4所示.
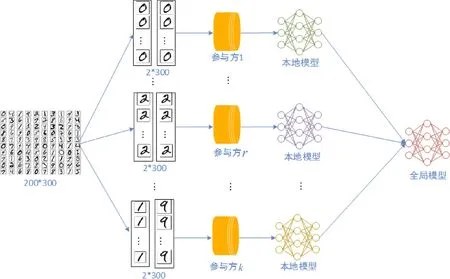
图4 EMFedAvg整体流程图Fig.4 Overall structure of EMFedAvg
第一步,中央服务器选取卷积神经网络作为要训练的全局模型并随机初始化权重,把模型和权重发送到各个参与方,同时把MNIST分成non-IID的200片,分发给各个参与方;第二步,各个参与方利用分发到的数据作为本地数据,并行迭代训练本地卷积神经网络,这里各参与方只知道己方得到的数据而无法获知他方的数据情况;第三步,各参与方把本地更新的模型权重返回到服务器,服务器算出所有参与方的平均权重以及每个参与方的EMD距离,对EMD距离进行排序,淘汰EMD距离过大的异常值,与剩下的参与方进入下一轮联邦迭代,直到模型收敛或达到最大迭代次数为止;第四步,服务器把得到的最终联邦模型分发到各参与方,并应用到实际环境中.
3.5 实验结果
根据以上设置,EMFedAvg在MNIST数据集的实验结果印证了实验设想.EMFedAvg与FedAvg在测试准确率与实验迭代次数的对比如表1所示,其对应关系见图5.

表1 EMFedAvg与FedAvg在non-IID划分的MNIST上实验结果对比Table 1 Comparison of EMFedAvg and FedAvg on non-IID split MNIST dataset

图5 EMFedAvg与FedAvg的准确率对比Fig.5 Precision comparison of EMFedAvg and FedAvg
从表1以及图5可以看出,虽然刚开始时EMFedAvg比FedAvg收敛要稍慢,但在第60轮迭代的时候,准确率已经超过了FedAvg,在第80轮时超过FedAvg的最高准确率86.81%,且仍然有提升的趋势.实验最好的情况EMFedAvg比FedAvg测试准确率高了近5%,这是一个不小的提升,使得联邦学习在non-IID数据上的准确率首次超过了90%.虽然在达到最终最好结果的时候,EMFedAvg比FedAvg的迭代次数要多,但EMFedAvg没有任何数据共享,在每一轮联邦整体的迭代中,EMFedAvg的通信次数和通信量是更少的.因此,EMFedAvg是一个高效、准确的算法,同时能够使得各参与方数据不出本地,很好地保护了数据隐私与安全.
4 总结与讨论
联邦学习技术使数据不出本地的分布式模型训练成为可能,是平衡数据隐私保护与人工智能发展的新兴技术.FedAvg是联邦学习的经典算法,本文在FedAvg的基础上结合样本分布与总体分布偏差的EMD距离,并对超过第三四分位数的异常值进行处理,留下优质参与方进行后续训练,使得FedAvg在non-IID场景中的效果得到了很好的提升.EMD距离衡量了各参与方数据分布与联邦整体分布的差异,可以用来衡量各方的贡献度,为联邦学习系统的效果激励提供了度量参考.
为了更切实地模拟真实环境中的non-IID场景,后续可以尝试在对数据进行non-IID分割的时候,发放给参与方不同数量的数据片,使各参与方在样本数量上形成不均衡这一极端情况.
人工智能技术发展到现在,数据隐私保护是一个不得不重视的问题.当前人工智能技术在数据隐私保护问题上的研究是比较欠缺的,研究如何能保护数据隐私的同时又使得海量数据能够得以发挥应有价值、解决数据孤岛问题的人工智能技术意义重大.基于这些原因,联邦学习近两年得到了极大的关注,寻找一种安全、高效、符合法律监管要求的算法是这一领域后续需要努力的方向.

