DNA计算中的可级联分子全加器
肖 玮, 强小利
(广州大学 计算科技研究院, 广东 广州 510006)
1 简 介
DNA是生物遗传信息的天然载体,它也可以作为可编程计算纳米材料使用[1].研究人员使用人工合成DNA编码序列实现了诸如可编程DNA纳米结构[2-5]、DNA信息存储[6-7]、分子逻辑计算[8-10]等.
DNA计算模型首先由Adleman[11]于1994 年提出.它的最大优点是充分利用了DNA分子具有海量存储的能力, 以及生化反应的海量并行性[12].近些年,许进等在利用DNA性质进行高效计算上有较大突破[13-14].DNA计算的一个重要研究方向是DNA链置换技术(DSD)[15].DNA链置换是在DNA粘贴模型基础上发展起来的一种动态DNA分子计算方法[16],它可以通过脚点完成各种复杂的动态DNA粘贴反应.DNA分子逻辑电路的实现需要由很多基础门电路组成,而DNA链置换技术在组成各种基础的分子门电路上给研究人员提供了极大的便利,可以说,DNA链置换技术促进了DNA计算研究的发展,在DNA计算机的研究中起着至关重要的作用.
在之前的一些研究工作中,很多研究人员通过级联组合一些简单的门电路,实现了复杂的逻辑电路系统,如2006年,Seelig等[17]构造了三种基本逻辑门,包括AND、OR和NOT逻辑门,并通过级联形成多层逻辑放大器电路,其分子逻辑运算的反应机制完全依赖于链置换和序列识别.2011年,Qian等[18]通过DNA链置换的级联实现了Hopfield联想记忆神经网络计算.该网络使用112条不同的DNA链组成4个完全连接的Hopfield网络联想记忆计算过程.为了组装大规模的电路,Qian等[19]提出了跷跷板逻辑门并验证了其能力,将其级联并并联到大规模逻辑电路中.近些年,Zhang[20]开发了一种基于逻辑的方法,通过级联DNA链位移来操纵硫化DNA物种与AuNPs的结合.利用该方法,建立了多个基于逻辑的操作系统,同时引入了多种DNA信号.这些研究都证明了DNA分子构建的逻辑运算系统具有独特的可编程逻辑计算能力和级联扩展功能.但是,目前基于DNA链置换逻辑电路的实现大多过于繁琐,需要高超的实验技巧,难以大规模应用于实验室操作实现.
针对现有的DNA链置换逻辑电路实现过于繁琐的难题,笔者提出了一种新的更加简洁高效的分子全加器的实现方法,通过国际通用的DNA链置换仿真软件Visual DSD进行了仿真计算分析,该软件是牛津大学的Lakin等[21]通过描述DSD编程语言和编译器实现的.仿真结果表明,这一全加法电路具有很好的稳定性,具备大规模级联组装实现基于全加器的四则运算分子电路系统的潜力,本文为分子计算模拟大规模逻辑运算电路的研究提供了理论基础.
2 方 法
2.1 基础逻辑门
本文设计的加法器逻辑电路由与门和异或门组成,通过DNA链置换设计了这两种基本电路门,并且构造了一个多输入全加器,这些门的结构如表1所示.半加器的电路结构如图1所示,全加器的电路结构如图2所示.
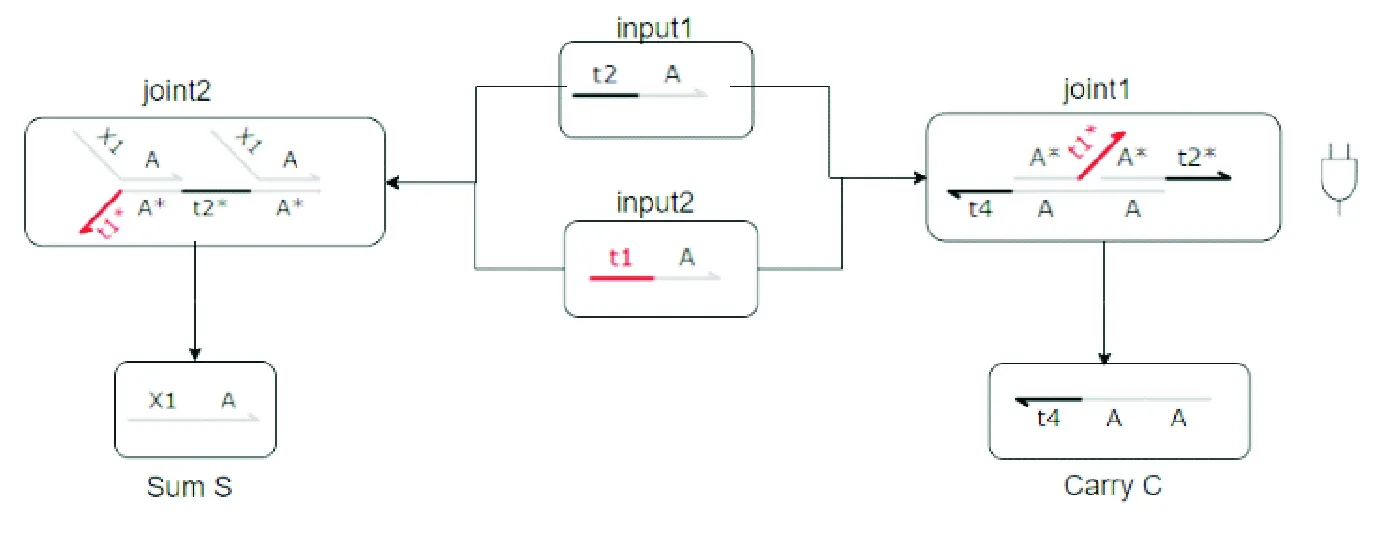
图1 半加器的电路结构Fig.1 Logic circuit structure of the half adder
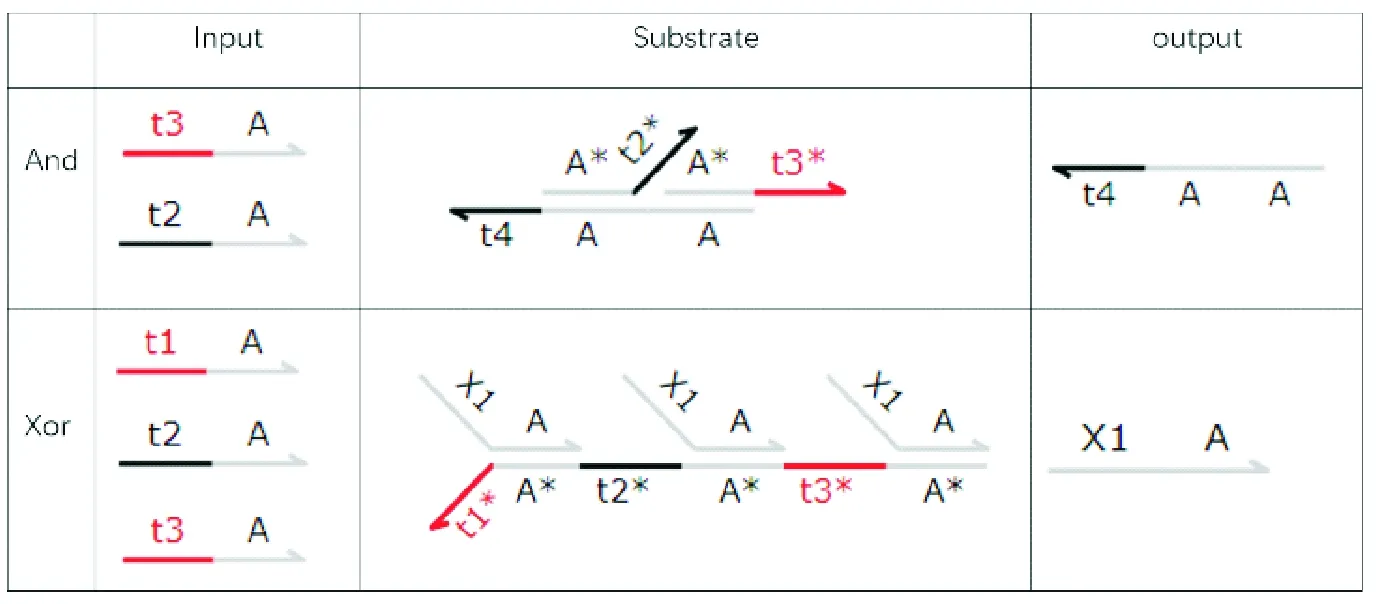
表1 两个基础电路门(与门和异或门)Table 1 Basic circuit gates (and gate and xor gate)
异或门由一个包括t1,t2,t3三个不同脚点域的基底构成,当输入链进入异或门发生反应后,会置换出带有荧光标记的信号链,通过信号链的浓度来判断输出的结果,DSD模拟实验可以证明,当输入链和基底全都过量时,通过设定joint4(图2)的浓度就可以知道信号链在各种输入情况下对应的浓度.图3为各种情况下输入对应的荧光值柱状图.图3可见,当joint4设定为100 nM时,信号链的浓度会固定在0,100,200,300这四个值之间,当浓度为0和200时输出“0”,当浓度为100和300时输出“1”.通过模拟实验可以发现,这样设计异或门的好处在于反应过程简单,避免生产过多复杂的产物干扰其他的反应过程.虽然有四个输出,但通过判断浓度可以得到二元结果,因此该方法可以应用于二元系统.
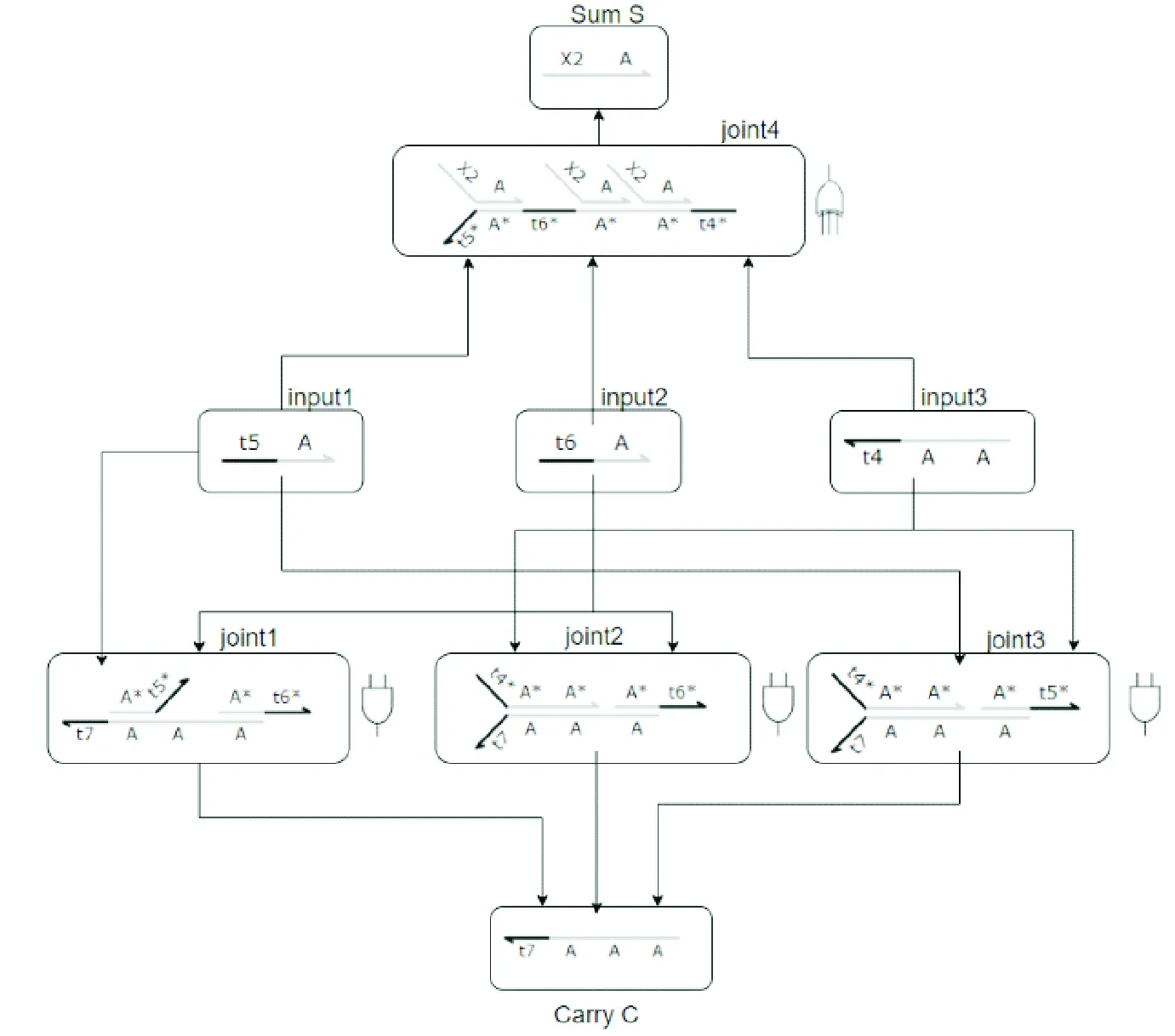
图2 全加器的电路结构Fig.2 Logic circuit structure of the full adder
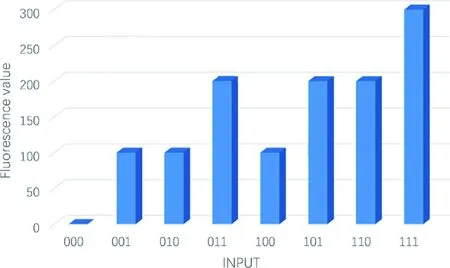
图3 各种情况下输入对应的荧光值柱状图Fig.3 Histogram of fluorescence values corresponding to various inputs
2.2 逻辑电路
利用这两个基本逻辑门,构造一个加法器的逻辑电路.该电路的结构如图2所示.
由图2可见,初始输入链为带有脚点域t1和域A的input1、带脚点域t2和域A的input2以及带脚点域t3和域A的input3.当input1,input2和input3输入时,会同时和joint1,joint2,joint3进行与门反应以及和joint4进行异或门反应.当input1,input2,input3传输到joint1,joint2,joint3时,它们将会和里面的基底发生反应.如果有2个以上的输入,那就会产生代表进位的输出链c.在第二个反应途径中,input1,input2,input3传输到joint4中,并与其中的基底发生反应,产生代表加法结果的输出信号链s.可根据信号链的浓度来判断加法结果是“1”还是“0”.真值表如表2所示,反应网络如图4所示.
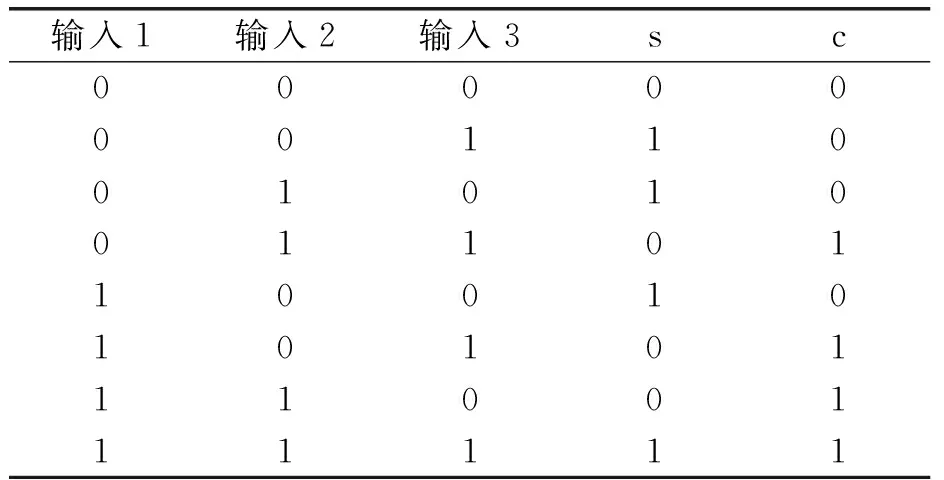
表2 逻辑电路真值表Table 2 Truth table of the logic circuit
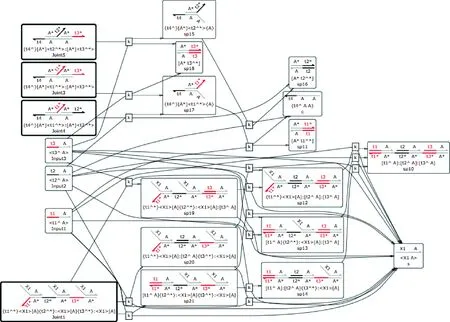
图4 全加器逻辑电路的反应网络Fig.4 Reaction network of the full adder logic circuit
仿真结果(图5)和真值表(表2)根据不同的输入显示输出信号.仿真实验中除了joint4设定为100 nM,其他的反应物都设定为过量(5 000 nM),这样的设定一是为了固定信号链s的浓度,方便之后做级联电路的时候可以提前知道代表“1”和“0”的浓度,二是为了产出大量的进位链C,这样才能使级联的下一个反应中进位链C可以达到过量.
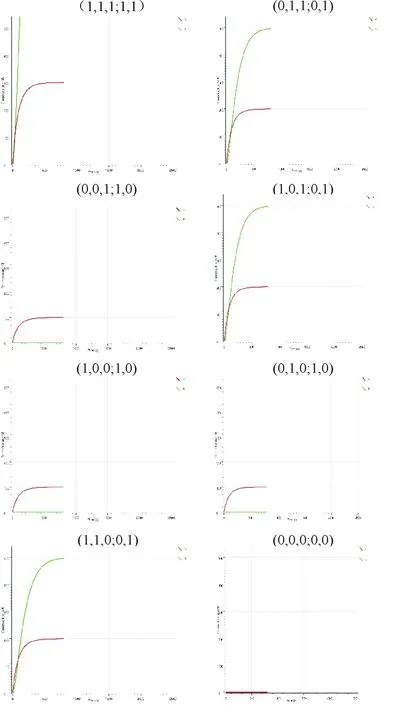
图5 逻辑电路的DSD仿真结果Fig.5 DSD simulation results of the logic circuits注:括号中的数字是代表各种情况的逻辑输入和输出.(输入1,输入2,输入3;加法结果s,进位c)
2.3 多位输入加法器
笔者将这两个反应集成到一个支持多位输入的级联加法器上,由于最终产物代表进位的链C和输入链具有一样的置换域,所以只需要在接下来的级联电路中替换掉以上逻辑电路中的一些脚点就可以实现.然后将四个一位加法器串联起来,就实现了四位加法器逻辑电路,仿真实验如图6所示.反应网络如图7所示.
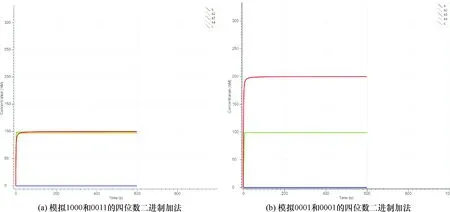
图6 仿真实验图Fig.6 Simulation experiment diagram
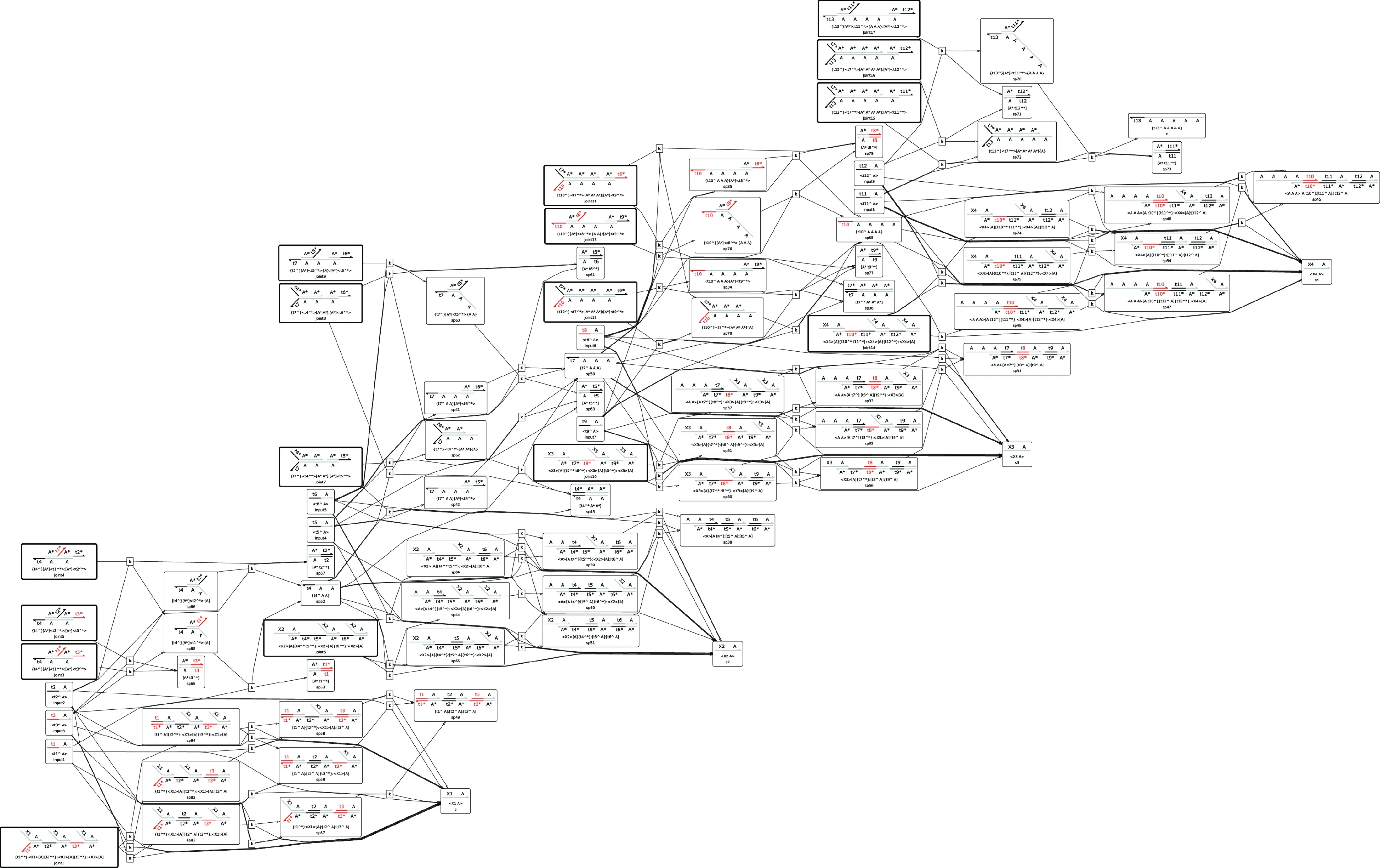
图7 多位输入加法器的反应网络,由DSD仿真软件自动生成Fig.7 Response network of multi-bit input adder automatically generated by DSD simulation software
每个加法器完成链置换反应后产出的进位链C都会比上一个域的进位链多一个A(图8).
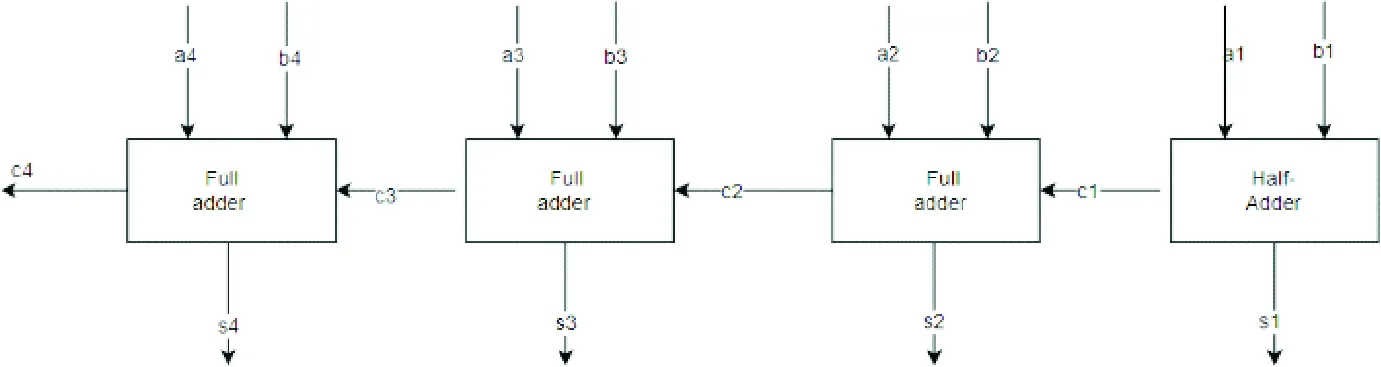
图8 四个加法器级联成为四位全加器Fig.8 Four-bit Full Adder using cascading four Adders
为了避免出现破坏上一个加法器与门规则的情况,在每个加法器的基底上也加了一个域A,每发生一次级联,下一个加法器的基底就要加上一个域A,这样可以保证上一个加法器中的秩序不会被破坏.每次级联之后进位链C的域变化如图9所示.

图9 每次级联之后进位链C的域变化Fig.9 Change of domain of carry strand C after each cascade
3 比 较
笔者与以前的一些研究[22-24]进行了比较,见表3~表5.DSD所需的能量来自分子热运动,其功耗和能耗都很低,因此,不需要比较功耗和能耗.所以在相同的输入条件下比较了反应时间.

表3 和Jiang研究的反应速度比较Table 3 Comparison with Jiang’s research on reaction speed
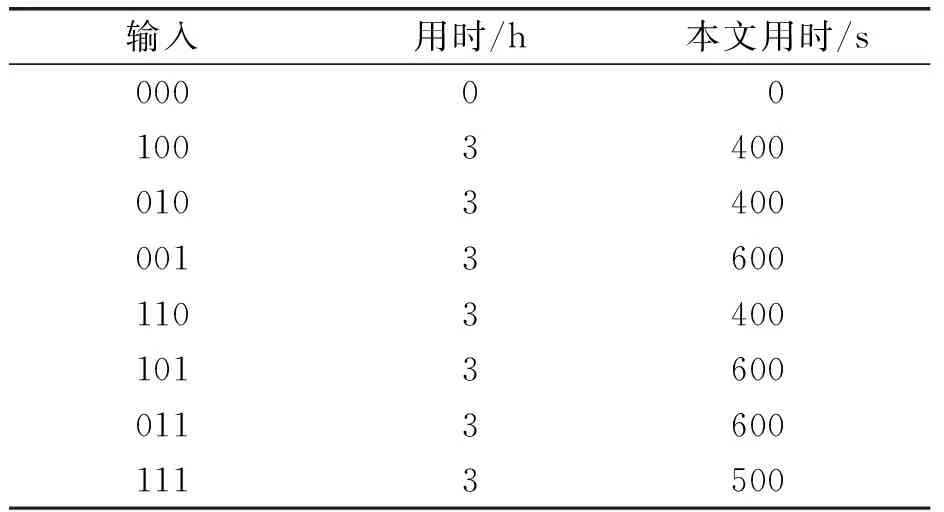
表4 和Lederman研究的反应速度比较Table 4 Comparison with Lederman’s research on reaction speed
4 讨 论
DNA分子计算的链置换反应机制是通过设定好的脚点域来精准地完成一系列可编程逻辑运算的生化反应过程,利用动态的脚点域能完成各种各样的DNA分子计算操作.由于DSD分子计算的动态特性,使得这一方法在进行分子运算逻辑设计的时候非常灵活和方便,一经问世就深受研究人员们的喜爱,但是也正是因为它的灵活性以及脚点域的不稳定性,导致反应中也会经常出现意想不到的副反应,有时候甚至会产生很复杂的二级产物以及泄露过程[25].本文的逻辑设计避免了这些问题,并通过Visual DSD模拟实验验证了该设计,这一方法只在逻辑电路中设计必要的域,让反应尽量少产出会产生干扰的二级结构,使得逻辑电路保持简洁高效.同时,基于这一原则设计的多种逻辑门构建的多位输入加法器也具有高效且简洁的优势,组成该全加器逻辑电路的基础门电路总和相较于同类研究的个数较少,涉及了更少的生化反应过程,也避免产出一些复杂的二级产物,整个反应过程高效且一目了然.进一步的研究可以通过修改脚点域,不断拓展这一加法器的输入位.整个系统的仿真实验结果表明,该电路具有强大的大规模计算能力和其他功能.这一研究为形成更复杂的分子逻辑电路结构和功能奠定了基础,为DNA计算、生物检测、纳米电路等领域的发展提供了新的编码设计思路.
—— “T”级联

