激光焊接裂纹磁光成像频域特征分析
杜亮亮,高向东,张南峰,季玉坤
(广东工业大学 广东省焊接工程技术研究中心,广州 510006)
引 言
焊接是现代工业中应用广泛的加工技术,焊接过程中容易受到焊接参量和外部环境的影响产生焊接裂纹,直接影响焊接产品的质量降低生产效率[1-3],因此对焊接裂纹进行检测尤为重要。而传统的焊接缺陷无损检测方法都存在一定的局限性,如射线检测对人体有辐射,超声检测需要耦合剂,漏磁检测只适用于铁磁性焊接材料的检测等。本文中研究了基于法拉第磁光效应的磁光成像无损检测新方法,通过旋转磁场励磁,获得缺陷处周围的漏磁场,生成缺陷磁光图像,提高缺陷无损检测效果。
目前国内外对数字图像的处理主要在空域、时域和频率域内进行。焊接裂纹的磁光成像检测主要在空域范围研究缺陷,反映空间域内裂纹灰度信息的分布情况。时域反映信号幅度随时间的演变,除信号分量的简谐波之外,难以明确地揭示信号的频率组成和每个频率分量的幅度[4-6],并且磁光图上的缺陷信息不是连续信号,无法从时域信息辨别缺陷,所以选择从频域角度对缺陷磁光图像进行分析。对图像信号进行频域上的处理,即将信号基于傅里叶变换分成不同频率成分[7],对裂纹磁光图像进行图像变换主要是进行2维离散傅里叶变换,获得包含裂纹信息的频谱图,提供比时域信号波形更丰富和更直观的信息。变换后图像的高频成分大部分是图像噪声和缺陷轮廓,低频成分是背景部分和图像中变化较慢的部分。对图像进行傅里叶变换后,图像能量主要集中在低频段上,包含图像的基本外形轮廓特征和总体灰度特征[8-9],这对图像的压缩和传输都比较有利,而且使得运算次数减少,节省运算时间,便于缺陷信息的提取和识别[10]。
作者在参考文献[11]的基础上,从频域的角度进一步研究旋转磁场焊接裂纹的磁光成像,通过对裂纹磁光图像在频域上进行2维离散傅里叶变换,分析不同采样时间裂纹频谱图特征,得到旋转磁场下焊接裂纹磁光成像规律的频域特征,分析焊接裂纹磁光成像规律在空域和频率域上的对应关系,从频域的角度进一步验证旋转磁场下焊接裂纹磁光成像规律的正确性,为焊接裂纹检测提供试验基础,提高缺陷磁光成像无损检测效果。
1 2维离散傅里叶变换
傅里叶变换是常见的正交变换,应用广泛,在数字图像的分析、增强和压缩中起着重要作用[12]。傅里叶变换是作为自变量的“信号”与“频谱”之间的转换关系,将函数变成了一系列的周期函数,其物理意义是将图像从空域变换到频域的分析。傅里叶变换之后,信号可以在一个新的频率空间被识别,在时域中更为复杂的问题可以在频域中被简化,从而简化了分析处理步骤,信号可更好地在频域中表示。傅里叶变换包含连续、离散、快速和短时傅里叶变换,其中2维离散傅里叶变换在处理数字图像处理时应用的最广[13-14]。
对焊接裂纹磁光图像进行2维离散傅里叶变换,假设1帧磁光图像的大小为M×N,它的离散函数可以看作是f(x,y),其中x=0,1,…,M-1;y=0,1…,N-1[15]。2维离散傅里叶变换F(u,v)定义为:
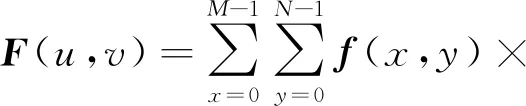
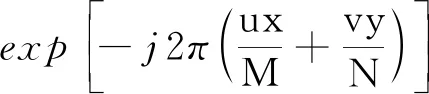
(1)
式中,u=0,1,…,M-1;v=0,1…,N-1。
根据2维傅里叶变换的定义,即使原图像f(x,y)是实数矩阵,它的2维傅里叶变换的结果通常也是复数形式。因此一般以计算图像函数f(x,y)的傅里叶变换谱的方法来观察傅里叶变换结果。F(u,v)的实部和虚部可以表示为R(u,v)和I(u,v)[16],那么f(x,y)的傅里叶变换可定义为:
F(u,v)=R(u,v)+jI(u,v)
(2)
对于图像的频域分析,其特征量主要是频谱。原图像函数f(x,y)傅里叶变换的频谱定义为:
|F(u,v)|=[R2(u,v)+I2(u,v)]1/2
(3)
图像通过2维傅里叶变换获得的频谱图是图像的梯度的分布图,显示了图像的能量分布。如图1所示,焊接裂纹傅里叶频谱图上的明亮点实际上是灰度图上点与图像相邻点之间的差值,也就是裂纹灰度值差异的大小,即焊接裂纹在该点的频率[17]。如果梯度高,则该点的亮度高,否则该点的亮度低。如果裂纹频谱图上有较多暗点,则裂纹的实际图像更平滑,因为灰度图上点与附近的点没有太大差异,渐变也相对较小。相反,如果频谱图中有更多亮点,则实际图像表现为边界两侧明显,且有明确的像素差异。

Fig.1 Spectrum diagram of welding cracka—original graph b—the enlarged graph
图1中裂纹磁光图像是经过傅里叶变换得到的频谱图。靠近原点周围比较亮,四周比较暗,也就是这帧磁光图中低频部分份量多,高频部分份量少,符合图像识别时的直观感受。频谱图中频率较低的部分一般是物体的主体、背景等。离原点越远,频率越高,对应图像中像素值变化速度快的部分,如物体的边界[18]。一张图片中通常也是边缘部分较少,颜色相近或灰度相近的主体区域较多。
对焊接裂纹磁光图像在频域上进行图像处理,获得对应的频谱图,通过对比分析所获得的傅里叶特征图的不同,探究频域下旋转磁场焊接裂纹磁光成像规律的特征,为焊接缺陷的无损检测和识别提供新的研究方法和依据。
2 焊接裂纹磁光成像试验系统
如图2所示,试验系统主要由钇铝石榴石(yttrium aluminum garnet,YAG)激光器、旋转磁场发生器、磁光传感器及计算机组成。本文中试验样本采用如图3所示的模拟裂纹。由YAG激光器焊接两块低碳钢板得到,用微小间隙模拟微裂纹,低碳钢板参量为200mm×80mm×2mm。激光焊焊接峰值功率为1kW,焊接速率为2.5mm/s,脉宽为6ms。选取磁粉探伤仪作为旋转磁场发生器,其两相交流电相位角和交叉角都为90°。用旋转磁场发生器对图3中的感兴趣区域励磁,通入旋转磁场发生器的电源为200V,50Hz;旋转磁场发生器励磁电压为150V,频率为50Hz;磁光传感器的提离值为3mm,采样频率为75Hz;磁光图像大小为400pixel×400pixel。由磁光传感器采集包含裂纹信息的动态磁光图,通过分析所获磁光图中第1帧磁光图的变化来研究旋转磁场工频激励下的成像规律。
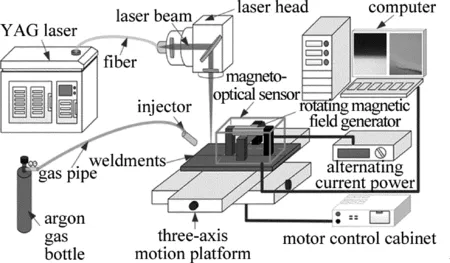
Fig.2 Experimental setup of weldment magneto-optical imaging under rotating magnetic field excitation

Fig.3 Physical diagram of weld cracks
3 试验结果与分析
由旋转磁场激励下的裂纹动态磁光成像可知,在旋转磁场两个励磁周期(40ms)内,磁光传感器可采集连续3帧动态磁光图像[19-20]。以同样的焊接裂纹和试验参量进行两次试验,获得两次试验数据,每次试验数据采集1200帧裂纹磁光图。分析过程中将分别采集到的1200帧磁光图以3帧一组依次分成400组,每组中的3帧磁光图分别定义为第1帧、第2帧、第3帧,以第1组的3帧磁光图作为初始3帧磁光图,把这400组磁光图按顺序排列,对比分析所有组中第1帧磁光图的变化,按次序提取当中第1帧变化最明显的几组磁光图。第1次试验数据中提取了9组焊接裂纹第1帧变化明显的磁光图像,第2次试验数据中提取了7组焊接裂纹第1帧变化明显的磁光图像。
为了获得旋转磁场焊接缺陷磁光成像规律在空域和频域上的区别,对所获得的两次试验数据进行2维离散傅里叶变换,得到裂纹对应组别第1帧磁光图像的频谱图,通过分析频谱图的变化和亮度情况研究旋转磁场磁光成像规律的频域特征,分析焊接裂纹磁光成像规律在空域和频率域上的对应关系,从频域角度对旋转磁场成像规律进行解释和验证。
3.1 焊接裂纹磁光图像的频谱图对比
第1次试验数据中提取的9组第1帧焊接裂纹磁光图像如图4所示。图4a~图4i分别对应第1组~第9组。其中图4a中间变化部分为缺陷区域,中上半部分和下半部分均为无缺陷区域。对这9组第1帧磁光图像作2维离散傅里叶变换,得到对应的频谱图。由于图像原始频谱图中心对应低频分量一般较少,难以区别其特征,因此将对应的9组裂纹频谱图按相同比例放大得到对应的9组频谱放大图,如图5所示。图5a~图5i分别对应第1组~第9组。

Fig.4 9 groups of the first frame of crack magneto-optical images in the first test data

Fig.5 The enlarged spectrum images of 9 Groups of the first frame of crack magneto-optical images in the first test data
从图5中可以看出,裂纹第1次试验数据中,第1组~第9组频谱图的整体变化趋势为:第1组~第3组频谱放大图逐渐变小,第3组~第5组频谱放大图慢慢变大,第5组~第7组频谱放大图又逐渐变小,第7组~第9组频谱放大图又慢慢变大。
为了验证频谱放大图变化规律的正确性,以第2次试验数据提取的7组第1帧焊接裂纹磁光图像为研究对象,如图6所示。经2维离散傅里叶变换得到对应的频谱放大图如图7所示,图7a~图7g分别对应第1组~第7组。

Fig.6 7 groups of the first frame of crack magneto-optical images in the second test data
从图7中可以看出,裂纹第2次试验数据频谱图的整体变化趋势与第1次试验数据频谱放大图的整体变化趋势截然相反:第1组~第3组频谱放大图逐渐变大,第3组~第4组频谱放大图慢慢变小,第4组~第6组频谱放大图又逐渐变大,第6组到第7组频谱放大图又慢慢变小。

Fig.7 The enlarged spectrum images of 7 groups of the first frame of crack magneto-optical images in the second test data
3.2 焊接裂纹磁光成像规律频域特征与空域特征对比分析
为了更好区别焊接裂纹同一组试验数据中频谱图的特征,统计分析每组频谱图上最亮的点,即统计灰度级为255的点,通过数字统计亮度的变化来确定频谱图上低频分量大小变化情况。表1和表2分别为焊接裂纹两组试验数据中灰度级为255的点的个数。

Table 1 Point number with gray level of 255 of spectrum images in Fig.5

Table 2 Point number with gray level of 255 of spectrum images in Fig.7
由图8可以看出,表中每组灰度级为255的点的个数变化和图5中得到的频谱图整体变化趋势一致,都为第1组~第3组频谱放大图变小,第3组~第5组频谱放大图变大,第5组~第7组频谱放大图又变小,第7组~第9组频谱放大图又变大。针对焊接裂纹第1次试验数据,结合图5和图6可以看出,裂纹9组对应频谱图上行方向变化较小,主要为竖直方向上变化明显,对应在图4的磁光图上,说明磁光图上水平方向差异大变化剧烈,这也体现了图像的频域特征和空域特征有一定的对应关系。而在频谱图上表现基本相同的第1组、第5组和第9组,以及第3组和第7组,在磁光上表现的却不尽相同。这也充分说明了虽然图像的频域特征和空域特征有一定的对应关系,但也不是完全对应,频谱图上表现更多的是磁光图空域中灰度变化快慢的程度。
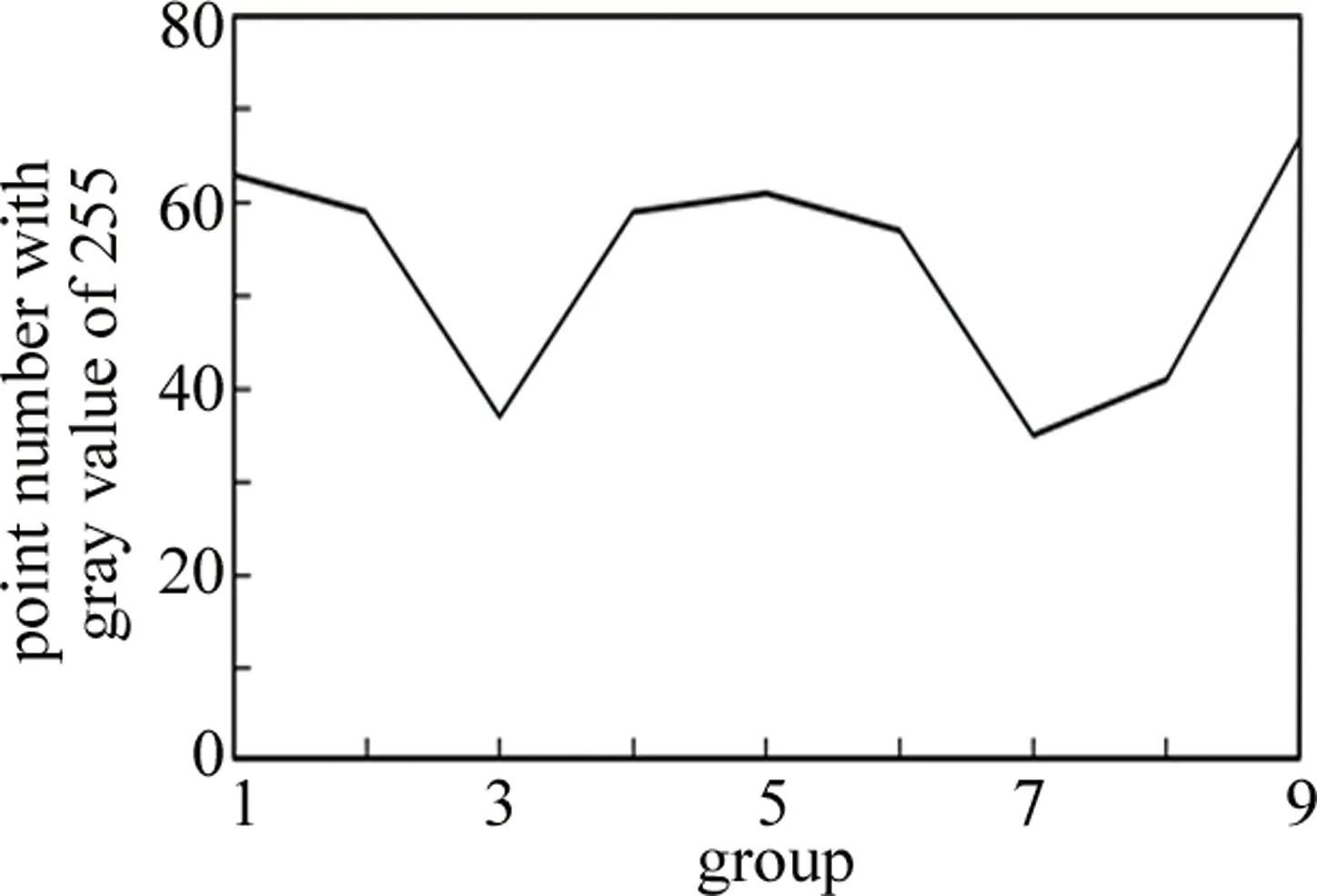
Fig.8 The change of points with gray level of 255 in Table 1
针对焊接裂纹第2次试验数据,由图9可以看出,表中每组灰度级为255的点的个数变化和图7中得到的频谱图整体变化趋势一致,都为第1组~第3组频谱放大图逐渐变大,第3组~第4组频谱放大图慢慢变小,第4组~第6组频谱放大图又逐渐变大,第6组~第7组频谱放大图又慢慢变小。结合参考文献[11]中图8,观察第1帧磁光图的变化过程,如果两帧缺陷磁光图像在旋转磁场圆形上的同一条对角线上采集,虽然表现在磁光图上这两帧磁光图不尽相同,但这时两帧磁光图像周围的磁场强度是相同的,所以表现在频域上,灰度级大小也相近,误差不大,见表2中的第1组、第7组和第4组;第2组与第5组;第3组与第6组。
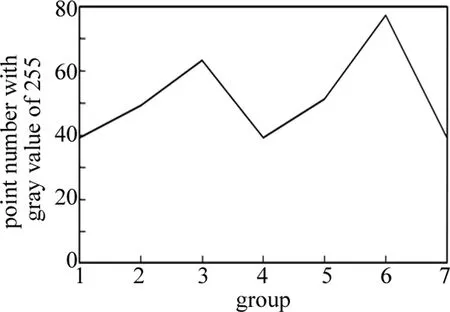
Fig.9 The change of points with gray level of 255 in Table 2
由参考文献[11]可知,旋转磁场激励下焊接裂纹磁光成像规律是表示为:任意一帧磁光图随着励磁时间的推移都会发生变化,经过885帧磁光图后回到初始状态。在频域范围内,旋转磁场磁光成像规律对应的频域特征表现为在一个变化周期(885帧磁光图)内,对应频谱图上会出现先变小再变大、再变小再变大或相反(先变大再变小、再变大再变小)的变化过程,这是由于分析选择时的起始帧不同,所以造成变化的过程也有差异。但是无论频谱图最初是变小还是变大的过程,在这个周期内焊接缺陷的频谱图最终会变回初始状态。在空域上每一帧磁光图的变化都可以定义为以初始3帧磁光图为一个循环周期,依次向下一帧转换。由于一个周期内频谱图会出现先变小再变大、再变小再变大或相反的情况,包含4个变化过程,即磁光图上有一组变化对应频谱图中两个变化过程,说明在空域上这一帧磁光图的变化过程剧烈,这是所有焊接缺陷在旋转磁场激励下磁光成像的统一频域特征。虽然在频域上表现相同的几组,在灰度图上表现得却不一样,因为这是频域上的特征,反映的只是灰度图上变化的快慢,但是也能从频谱图的变化特征中反推缺陷在空域内的形状分布特征和变化情况,可以作为焊接缺陷的无损检测和识别的参考。
4 结 论
激光焊接裂纹磁光图像的频域特征和空域特征有一定的对应关系,裂纹磁光图像经过2维离散傅里叶变换后得到的频谱图,可以看出,焊接裂纹在频域上的成像特征,频谱图的亮度对应空域中焊接裂纹磁光图像上灰度变化快慢的程度,频谱图上亮度越大,磁光图上灰度变化越大,裂纹变化也越明显。在频域范围内,旋转磁场激励下激光焊接裂纹磁光成像规律对应的频域特征为:在一个变化周期(885帧磁光图)内,对应频谱图上会出现先变小再变大、再变小再变大或相反的变化过程,最终变回初始状态。进一步验证了旋转磁场下裂纹磁光成像规律的正确性,为焊接缺陷的无损检测提供了一种新方法。

