高水头船闸阀门顶止水安装变形试验与数值模拟*

魏述和，王 新

(1.凯里学院 建筑工程学院，贵州 凯里 556011；2.南京水利科学研究院，通航建筑物建设技术交通行业重点实验室，江苏 南京 210029)

当前，船闸建设正朝着高水头的方向持续发展，也对船闸阀门止水的水密性提出了更高的要求。船闸阀门顶止水初始安装位置的确定与其安装变形及受力特性密不可分，直接关系到阀门水封系统的工作可靠性和使用寿命。三峡船闸反弧门顶止水历次更换中，止水橡皮在阀门全关位置紧贴门楣，拧紧压板后在螺栓预紧力作用下，止水橡皮在门楣处压缩变形约2 mm，通过几年运行发现，这种初始安装位置要求对20～30 m的工作水头是合适的，但对于三峡中间级船闸40 m以上的工作水头并不合适，止水使用寿命无法达到预期[1]。因此，研究阀门顶止水的安装变形特性具有重要意义，可为止水初始安装位置的确定和顶止水变形预测提供依据。

止水安装变形研究大多是关于水工钢闸门。陈五一等[2]采用数值仿真和模型试验相结合的方法，对伸缩式水封水密性及封水判断依据进行研究，建立基于封头接触宽度和接触应力的判断依据，但只适用于特殊形式的伸缩式水封；刘礼华等[3]根据伸缩式止水的受力特点，设计一种水库库压自行封闭的高压闸门止水，并结合某大型水电工程进行试验研究，得出高压闸门止水水密性的变化规律和封头间隙对此的影响；杨斌等[4]采用数值仿真研究充压伸缩式水封封头外伸特性，计算多工况的临界封水背压值并与试验结果对比，认为计算仿真可信度高，可采用仿真计算代替试验，从而显著降低试验成本；张绍春等[5]通过某高水头弧形闸门伸缩式水封的切片试验，研究3种不同形式止水的变形及封水性能，认为伸缩式水封中采用软硬不同的复合断面性能最佳；王新等[6]研发止水切片试验方法，研究了半圆头型顶止水的变形特性。然而，高水头船闸普遍采用的反弧门半圆头型顶止水，与水工钢闸门的止水形式和工作特性差异很大，其安装变形特性的相关研究很少。从物理模型与数学模型的互补性考虑，本文采用试验与数值模拟相结合的方法，对高水头船闸阀门半圆头型顶止水安装变形特性进行研究。

1 研究方法

以高水头船闸反弧门半圆头型顶止水为研究对象，采用1:1切片试验和数值模拟相结合的方法，研究不同安装扭矩作用下止水的变形轮廓、位移、头部伸长、接触宽度等变形特征和按第四强度理论衡量的等效应力分布规律。

1.1 切片试验

研发的模拟反弧门顶止水安装条件的切片试验装置如图1所示。在阀门宽度方向，按两个安装螺栓布置宽度考虑，螺栓间距为120 mm，试验装置切片宽度取240 mm，安装螺栓横向对称布置，在装置侧面对应止水安装的位置布置有机玻璃观察窗，以便观测止水的变形。用于试验的顶止水试件见图2，取自工程实际使用的止水材料。止水安装采用自制的扭力扳手，可实时显示记录安装的扭矩值。止水安装按多个不同扭矩考虑，包括52.6、83.5、114.4、145.4 N·m，变形利用固定相机通过侧面有机玻璃观察窗观测，然后由计算机处理得到变形轮廓和变形量。

图1 1:1切片试验装置

图2 顶止水试件

1.2 数值模拟

切片试验可以模拟不同安装荷载作用下止水的变形特性，但无法获得止水的应力分布，因此，在试验的基础上，采用有限元数值模拟方法重点分析止水的应力特性。止水安装中涉及压板、止水、座板、胸墙等，它们之间有接触约束作用，数值模拟重点需要解决止水与各结构在边界上的接触问题。

令tSc是每个物体接触的整个面积，L为1和2分别表示物体I和J，则在时刻t给出的虚功原理为：

(1)

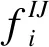
对应于时刻t线性化的有限元离散方程是：

(2)

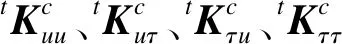
(3)

橡胶止水材料采用Mooney-Rivilin模型，通过对试验所用的橡胶进行材料力学试验，获得其应力-应变曲线如图3所示，进而拟合得到模型参数C01=445 722.2、C10=125 362.4，用于数值计算分析。采用平面应变假定，建立的止水二维模型网格如图4所示，所有与止水接触的面都设置接触条件，采用接触算法求解。胸墙和座板底部全约束，压板上表面施加荷载，荷载通过式(4)由安装扭矩换算得到：

(4)

式中：F为压紧力；T为扭矩；d为螺栓直径；Kt为换算系数。

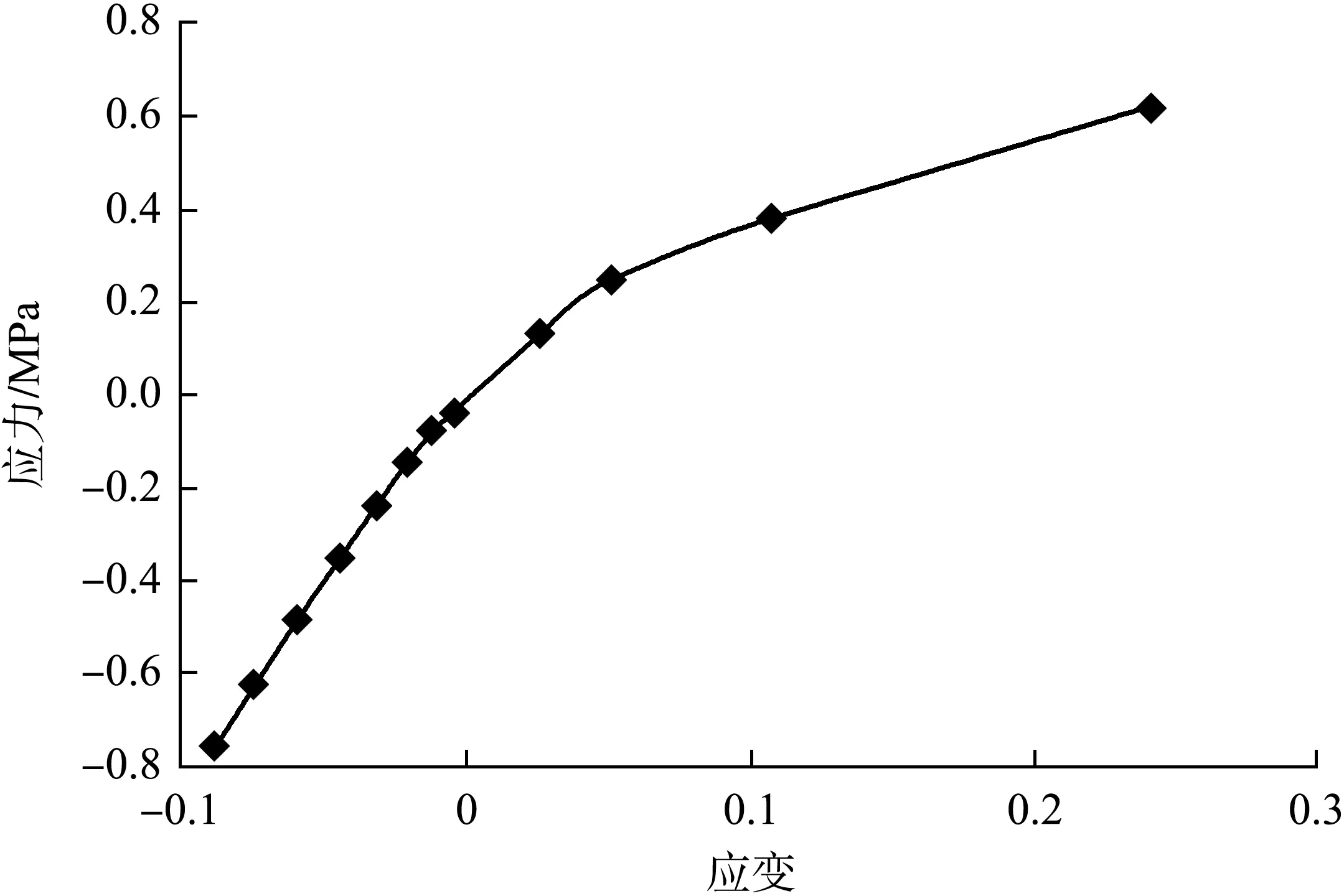
图3 止水材料力学试验曲线

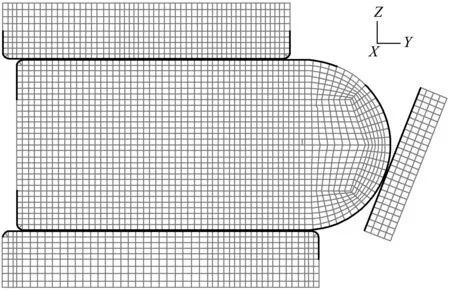
图4 止水有限元模型

2 结果分析

通过1:1切片试验和数值模拟分别得到了安装扭矩为0、52.6、83.5、114.4和145.4 N·m作用下的变形轮廓、头部凸起和接触宽度等安装变形特征，以及不同安装荷载作用下止水的应力分布。

2.1 止水安装变形

2.1.1变形云图

不同安装荷载条件下切片试验和数值模拟获得的止水变形结果如图5所示。左侧为试验照片，右侧为计算变形云图，试验和数值模拟结果显示，止水在逐渐增大的预紧扭矩作用下，压板挤压止水压缩变形，与上压板接触的止水上表面竖向压缩，止水头部向右伸长，并在倾斜胸墙的约束下，向上凸起；随着预紧扭矩增大，止水与胸墙接触愈加紧密，接触宽度逐渐增大；从变形特性看，试验和数值模拟结果吻合较好。

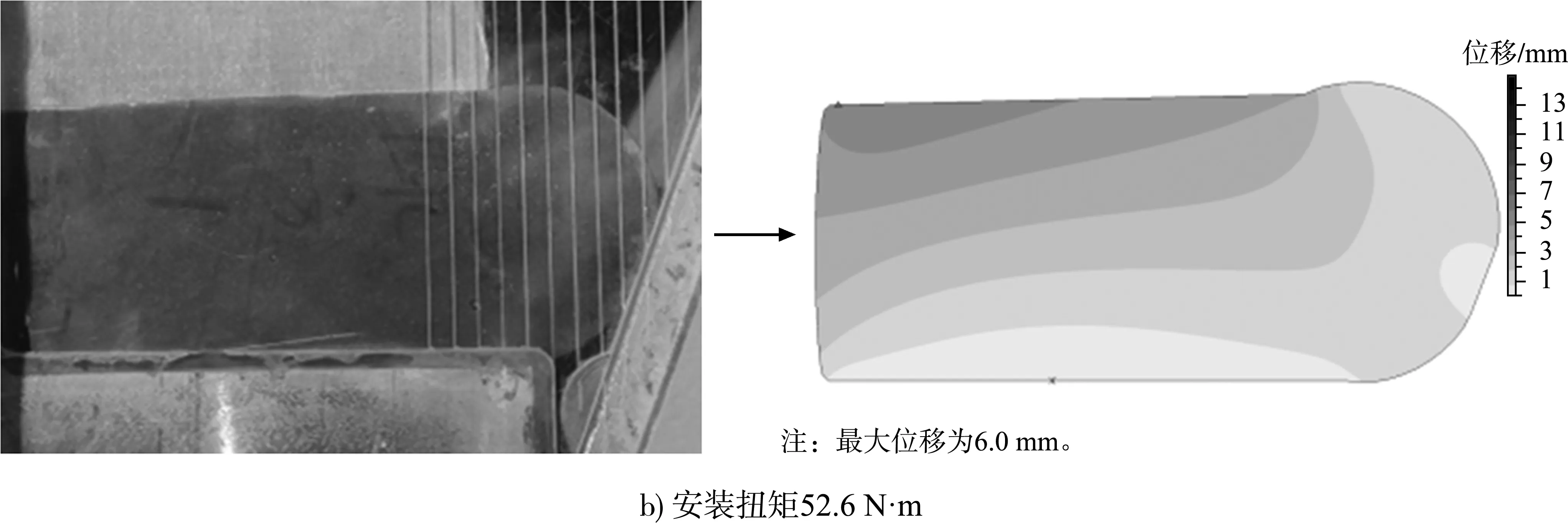
图5 止水安装变形试验和计算结果

2.1.2止水变形量

切片试验和数值计算止水头部变化轮廓对比见图6，图中实线为切片试验变形轮廓线，虚线为数值模拟得到的轮廓，倾斜细实线为胸墙位置。试验结果和数值模拟结果吻合较好，但止水头部右下部分在各级荷载作用下均出现偏差，其原因是数值模拟时在止水与胸墙接触处未产生相对滑动，而试验过程中观察到加载时止水与胸墙间产生了小幅度相对滑动。总体来看，数值模拟结果与试验结果轮廓线吻合度较好。

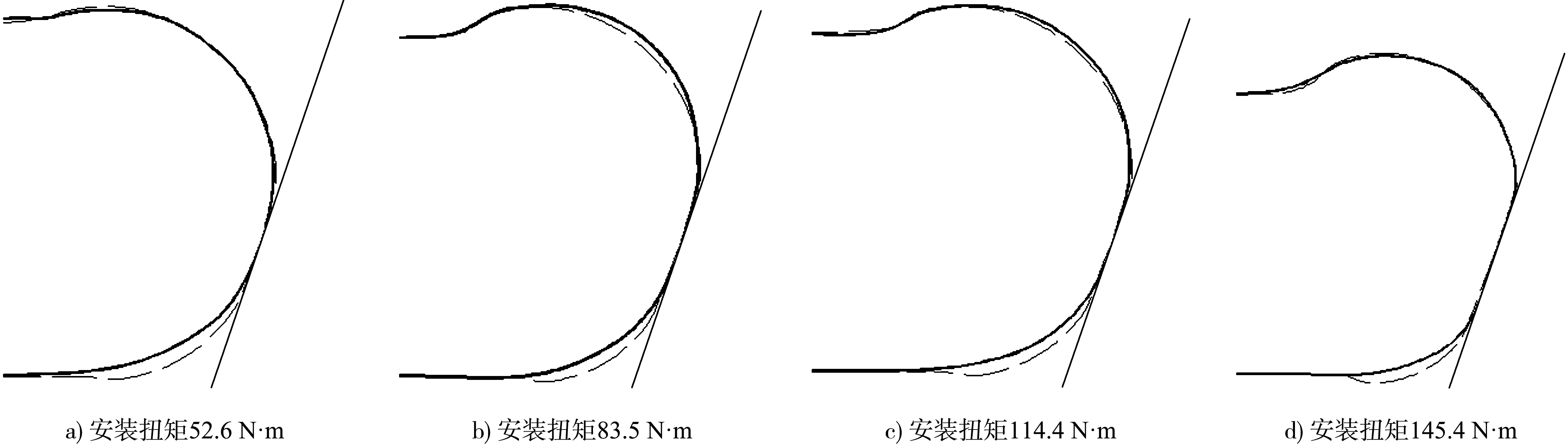
图6 切片试验和数值模拟结果对比

荷载逐渐增大，压板压紧止水，并且在止水座限制下头部受到挤压。止水从与垫板接触表面向上到与压板接触表面位移逐渐增大，半圆形头部由于受到倾斜胸墙的限制，位移变形小于压板下部区域的止水变形，预紧荷载增大时位移分布也是呈现同样规律；安装扭矩52.6 N·m，位移最大值为6.0 mm，出现在与压板接触表面的最左侧；安装扭矩为83.5、114.4、145.4 N·m，位移最大值分别为8.9、10.5和13.0 mm，最大值同样出现在相同位置附近。最小值均出现在与垫板接触的止水下表面和与胸墙接触的半圆形头部位置。

2.1.3止水头部凸起高度

从螺栓中心、止水上表面为基准，测量止水头部受门楣约束时的凸起高度。头部凸起高度变化如图7所示。未加载时，由于上压板的自重作用，止水受压，头部产生1.17 mm的凸起；逐渐加载，半圆头型止水头部向上凸起高度逐渐增大，切片试验结果显示，安装扭矩从52.6 N·m增大到145.4 N·m时，凸起高度从2.41 mm增大到8.47 mm，近似线性变化；数值模拟表明，同样加载方式凸起高度从3.27 mm增大到8.97 mm，与试验结果契合。研究表明，随着安装扭矩增大，头部凸起高度相应增大，变化近似线性。

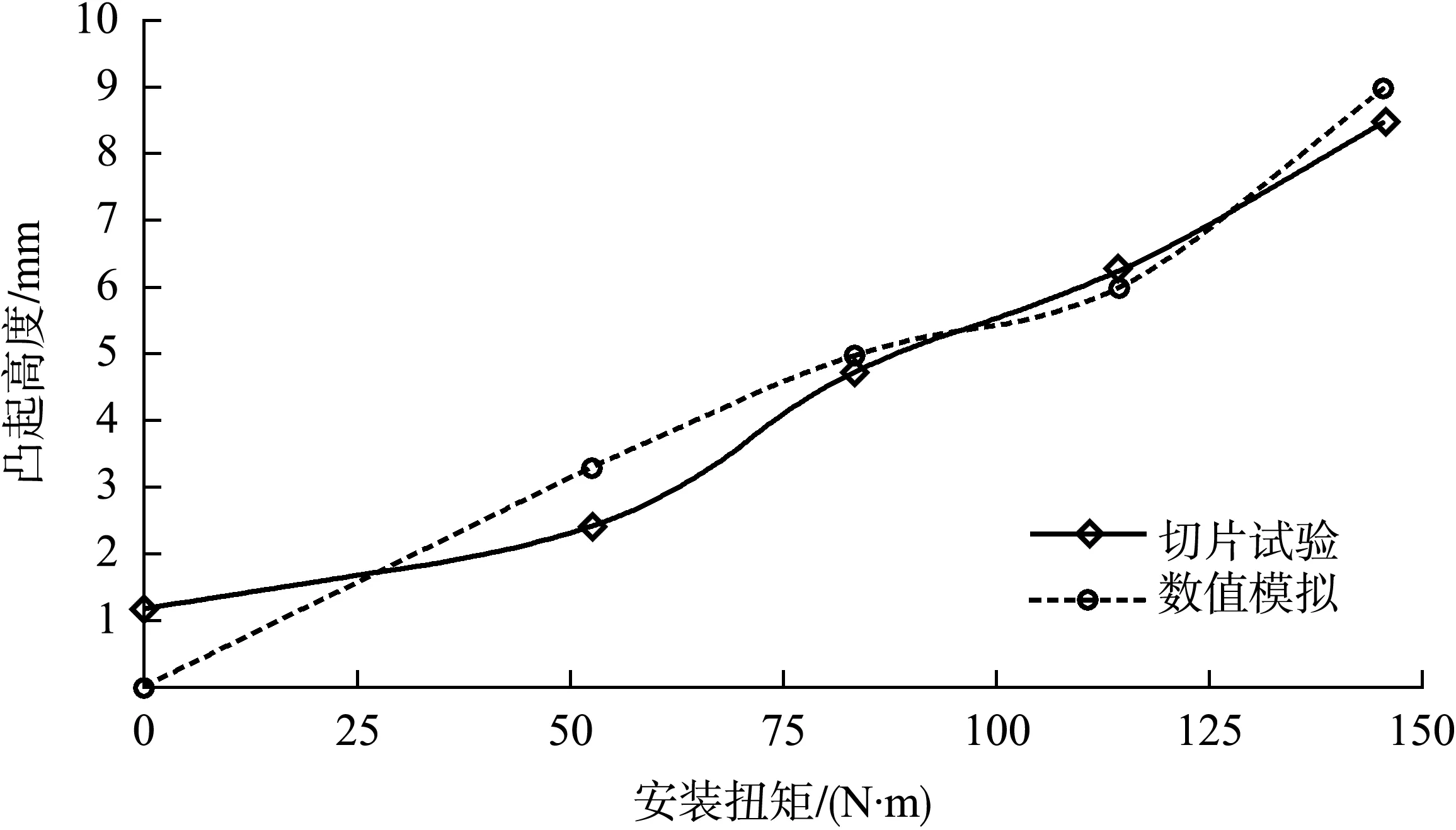
图7 止水头部凸起高度

2.1.4接触宽度

水密性与止水座板间的接触宽度密切相关，图8为止水座上止水橡胶的接触宽度变化曲线，安装扭矩增大，接触宽度相应增大。安装扭矩施加前，由于上压板的自重作用，止水受压，半圆形头部位置与止水座接触宽度为11 mm；逐渐加载，头部与止水座进一步压紧，接触宽度继续增大，切片试验结果显示，安装扭矩从52.6 N·m增大到145.4 N·m时，接触宽度从25.2 mm增大到33.2 mm，呈非线性变化趋势；数值模拟表明，同样加载时接触宽度从14.9 mm增大到24.1 mm，与试验结果变化规律相同。试验与数值模拟的接触宽度存在约10 mm的初始误差，这是由于试验加载前，上压板的自重所导致。分析表明，随着安装扭矩增大，止水座上橡胶接触宽度相应增大，呈非线性增大趋势。

图8 止水头部与胸墙接触宽度

2.2 等效应力

按第四强度理论，不同安装扭矩作用下止水等效应力的数值计算结果见图9。安装扭矩逐渐锚紧压板挤压止水，压板和垫板之间的止水部分处于相对高的等效应力状态，半圆形头部除了与胸墙接触的部位外，其余部位未受约束，处于低应力状态，逐渐增大安装扭矩等效应力呈现相同的分布状态。52.6 N·m安装扭矩作用下，最大等效应力出现在止水上表面与压板接触的两侧边缘处，为0.8 MPa左右，属于应力集中现象，其余大部分区域等效应力处于0.4 MPa的水平；半圆形头部处于相对低的等效应力水平，大部分不超过0.2 MPa，而受胸墙止水座约束而受挤压的部位等效应力显著增大，但未超过0.5 MPa。随着安装扭矩增大到83.5、114.4和145.4N·m，止水最大等效应力分别达到1.5、2.6和3.6 MPa，均出现在压板角点与止水接触位置。由加载过程止水应力分布特性看出，压板、座板与半圆头接触区域的应力梯度较大，加之阀门频繁启闭，止水反复变形，该位置最易发生损坏，与止水实际使用情况相符。

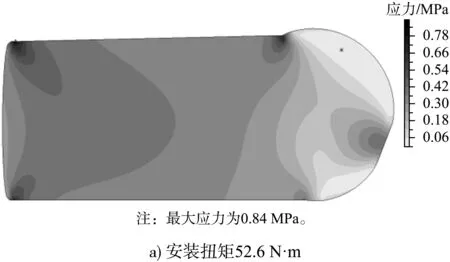
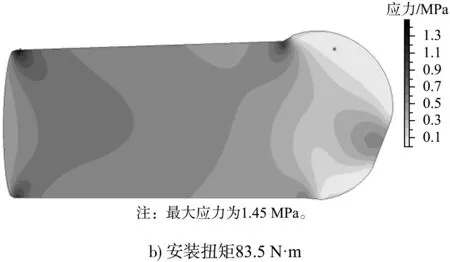
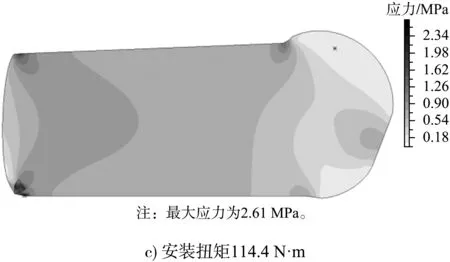
图9 等效应力云图(单位：MPa)

3 结论

1)基于力学试验获得原型材料参数和接触力学计算理论，止水变形数值模拟结果与1:1切片试验结果吻合较好，为止水应力、动力等数值分析奠定基础。

2)随着安装扭矩增大，止水头部凸起高度近似线性增大；胸墙与止水接触宽度呈非线性变化，增大速率随着安装扭矩增大而递减。

3)在各级安装扭矩作用下止水最大等效应力均出现在压板角点位置，属于应力集中现象；止水头部与压板、座板接触边界位置应力梯度最大，是止水最易发生损坏的部位。

4)本文仅研究了阀门止水的安装受力变形，水压作用下的变形规律及初始状态的叠加分析应做进一步研究。