频谱细化分数阶Fourier 变换的LFM 信号滤波算法

伍 龙，黄凯峰，肖理庆，徐小军

淮南师范学院机械与电气工程学院，安徽 淮南 232038

线性调频LFM（linear frequency modulation）信号是典型的非平稳信号，具有较大时宽带宽积，通过增加脉宽能够在较低的峰值功率下，可提高发射功率，增加探测距离。因此LFM 信号适合应用于雷达、无线通信、声纳等领域[1-3]。在无线通信系统中各类通信信号频谱相互重叠，且在信道传输过程中易受到自然界各种电磁波噪声的干扰，因此如何有效的抑制噪声和干扰是LFM 信号传输过程中需要解决的关键技术。

分数阶傅里叶变换（FRFT，fractional Fourier transform）对LFM 信号具有独特的处理优势，在分数阶Fourier 域内线性调频信号是带限的，基于这一特性，FRFT 非常适合处理LFM 信号，因此分数阶Fourier 变换在LFM 信号处理领域被国内外专家学者广泛深入研究[4]。文献[1]中采用的是经典分数阶Fourier 变换滤波的方法，该算法通过扫描二维时频平面寻找峰值最优阶数，以峰值为中心进行峰遮隔处理，选择合适带宽保留有用信号，进行相同阶次反变换，得到滤波后的信号，这种传统分数阶Fourier 变换算法适应性很强但计算量很大。文献[5]，提出一种基于分数阶Fourier 变换的量化噪声抑制方法，利用经典量化器的统计特性，分析得到在分数阶Fourier 域内量化噪声具有白噪声的特性，利用过采样和分数阶傅里叶域数字滤波方法对输入信号的量化噪声进行抑制，这种方法可以有效的滤除LFM 信号中的白噪声，但应用有一定的局限性。文献[6]对LFM 信号滤波的最优阶次FRFT 滤波方法，一种基于Radon-Ambiguity 变换和FRFT 的改进算法，将二维搜索降为一维搜索，减少了计算量。但在时频面上作一维搜索的计算量也比较大。参照文献[6]的思想，本文提出一种计算量更小的含噪LFM 滤波算法，首先通过分段解线调，估计出粗略调频率，然后通过频谱细化提高调频率的估计精度，再由调频率计算出FRFT 最佳变换阶次，在最优分数阶傅里叶域对含噪LFM 信号做窄带通滤波处理。

1 分数阶Fourier 变换

Fourier 变换是信号分析和处理的经典工具，但其并不适合用于非平稳信号的处理[7-9]。分数阶Fourier 变换作为一种新型时频分析工具，用分数阶Fourier 变换域内的单一变量，表征信号的时频特性，并且不会受到交叉项的困扰。在t域的信号x(t)的p阶FRFT 定义式[7]如式（1）所示：

Kp(u，t)=Aαexp[jπ(u2cotα-2utcscα+t2cotα)]K p(u，t)称为FRFT 的核函数；p为变换阶次，α=pπ/2(p≠2n)，n为整数，α为旋转角度。

分数阶Fourier 变换的逆变换可看作阶次为-p的FRFT，其公式如（3）所示：

令p=1，此时就是信号x(t)的傅里叶变换，可见傅里叶变换是FRFT 的一种特殊情况。

2 频谱细化FRFT 滤波算法

2.1 分段解线调

假设含噪LFM 信号x(t)的数学模型如式（4）所示：

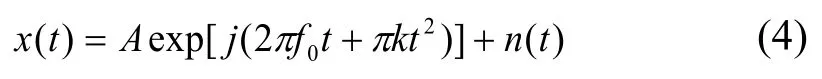
式中，A、f0、k分别为LFM 信号的幅度、初始频率、调频率，n(t)为加性高斯白噪声。

实际应用中，需要在t=nΔt时刻对x(t)进行采样得到离散信号，取其前N0/2 点和后N0/2，将它们进行逐点相乘，将它们进行逐点相乘得到的新序列为受噪声污染的正弦波，这个过程为分段解线调。对点乘得到的正弦波做FFT，则频谱峰值处所对应的频率是延迟N0/2 点后的频率改变量Δf，采样频率为fs时，实际延迟Δτ=N0/2fs，所以LFM 信号的调频斜率如式（5）所示：

如果延迟信号是在采样信号之前添补M0个零点得到的，那么M0就是实际的延迟，将延迟信号与原信号做分段解线调处理，便可以估计得到线性调频信号的粗略调频率。由于分段解线调无需搜索即可估计出LFM 信号的调频率，因此计算量比文献[6]中需要进行一维搜索的RAT 小。

2.2 频谱细化

由于分段解线调只能粗略估计LFM 信号的调频率，估计精度有待提高。若要提高调频率的估计精度，采样频率一定时只能通过增加FFT 的点数来提高FFT 的频率分辨率，实质即在整个频谱中均匀增加频域采样点数，计算量大为增加。可以先通过FFT 获取延迟相关谱主瓣所在位置，然后局部增加主瓣附近的频域采样点数，提高估计精度，这就是局部频谱细化[8]。采用chirp-Z 变换（CZT）实现局部频谱细化，CZT 的定义如式（6）所示：

式中，A=Aejθ0，W=Wejφ0，A为采样螺旋线起始点，W为描述轮廓上的点之间的复数比的

00复数标量m=0，1，…，M-1，M为频域采样点数。由，可得：

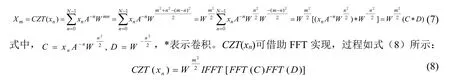
2.3 频谱细化FRFT 滤波算法步骤

（1）利用分段解线调方法，根据式（5）求出LFM 信号的粗略调频率kest；

（3）对含噪LFM 信号进行p0阶FRFT，如式（10）：

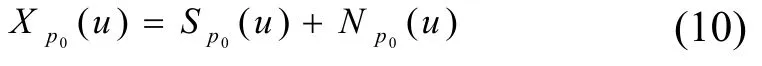
其中，Sp0(u)为LFM 信号的FRFT；Np0(u)为噪声的FRFT；

（4）利用窄带通滤波器在分数域内去噪[9]，如式（11）：

其中，Yp0(u)为滤波后LFM 信号的FRFT；W(u)是中心频率为u0的窄带滤波器。

（5）对经过滤波后的信号做-p0阶的FRFT，得到滤波后时域的LFM 信号y(n)。

3 频谱细化FRFT 滤波算法仿真

为了验证所提改进算法的有效性，在相同的仿真条件下，对比了频谱细化分数阶Fourier 变换和传统分数阶Fourier 变换滤波算法。

3.1 传统分数阶Fourier 变换滤波仿真

仿真选取的LFM 信号的参数[10，11]如下：初始频率f0=1 Hz，调频率k=15 Hz/s，幅度A=1 mV。观测时间为T=2 s，采样频率为fs=200 Hz，选用高斯白噪声作为干扰噪声，信噪比为10 dB。无噪LFM 信号的波形如图1 所示，加入白噪声的LFM 信号的波形如图2 所示，可以看到图2 的波形和图1 比较已失真严重，需要对其滤波后才可以恢复其信号特性。

图1 无噪LFM 信号波形Fig.1 Noise-free LFM signal waveform

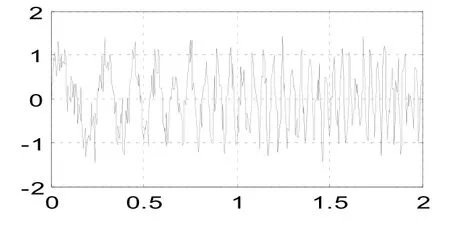
图2 含噪LFM 信号波形Fig.2 Noisy LFM signal waveform

利用传统的FRFT（本文采用Ozaktas 采样型FRFT）滤波，首先对含噪LFM 信号参数估计，得到最优变换阶次p0，然后在最佳变换阶次p0对含噪LFM 信号做分数阶Fourier 变换得到最优分数阶傅里叶域u0[12-14]。图3 为含噪LFM 信号u域的FRFT，得u域的最优采样点为277，利用分数阶傅里叶域的窄带通滤波器滤波后的LFM 信号如图4 所示，仿真程序计算可得到其SNRout=-2.98 dB。

图3 含噪LFM u 域的FRFTFig.3 FRFT in noisy LFM u domain

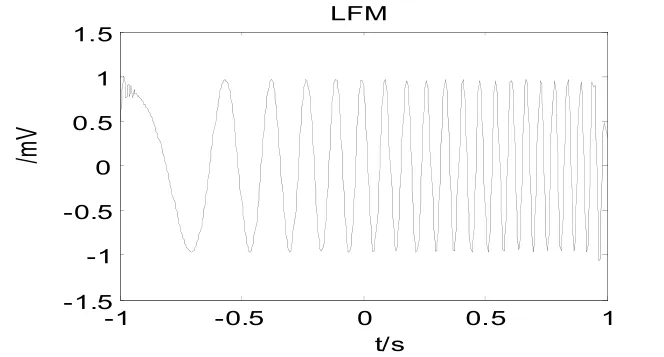
图4 传统FRFT 滤波后的信号Fig.4 Traditional FRFT filtered signal

3.2 频谱细化FRFT 滤波仿真

在相同的仿真条件下采用提出的频谱细化分数阶Fourier 变换滤波算法，将LFM 信号和其M0=100 点延迟逐点相乘，对得到的新信号做1024 点FFT 运算，得到的频谱如图5 所示。

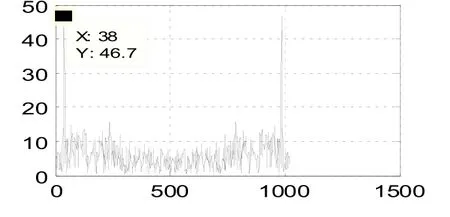
图5 延迟自相关频谱Fig.5 Delayed autocorrelation spectrum

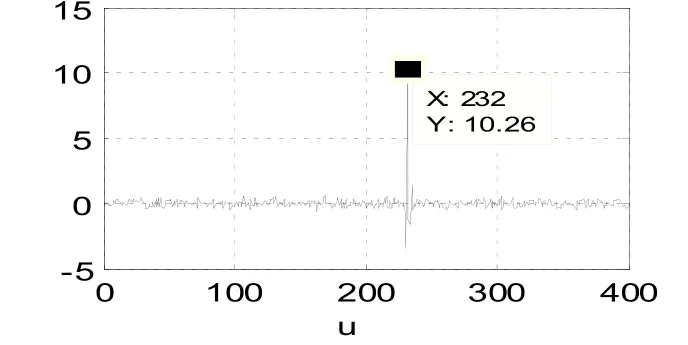
图6 分数阶傅里叶域上的幅度谱Fig.6 Amplitude Spectrum in Fractional Fourier Domain

可见，在频点38 处出现谱峰，利用式（4）计算出调频率为14.4531 Hz/s。为了获取更精确的调频率，在频率区间[37，39]内做chirp-Z 变换，求得调频率为=14.7207Hz/s。可以发现，经过chirp-Z变换后，求得的调频率更接近于实际值。根据式（6）求得LFM 的分数阶傅里叶变换阶次为p0=-0.0432，对LFM 信号做p0阶FRFT，由图6 可见，在u0=232处出现能量聚集现象。

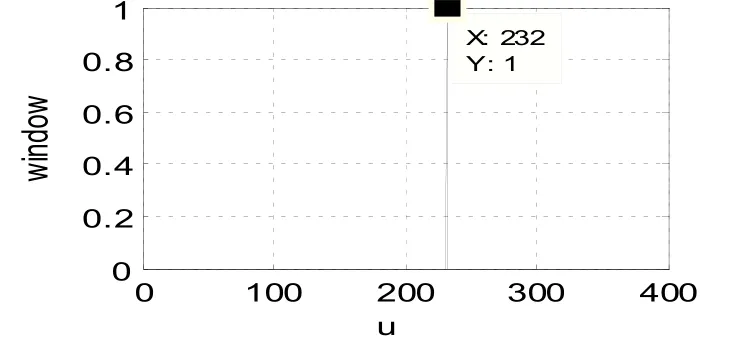
图7 窄带通滤波器Fig.7 Narrow bandpass filter

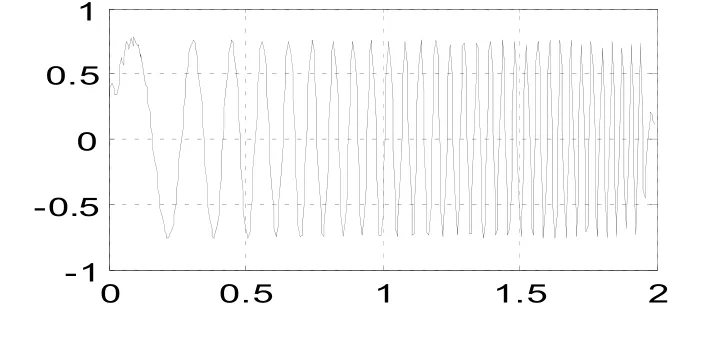
图8 频谱细化滤波后的信号Fig.8 Spectrum refinement filtered signal

选取的窄带滤波器如图7 所示，仅允许u0=232 处的信号通过滤波器。在分数阶傅里叶域滤波后对信号做-p0阶FRFT，得到滤波后的时域信号，如图8 所示。对比图1、图2 与图8，可见，经频谱细化FRFT 算法滤波后LFM 信号波形十分接近原无噪LFM 信号波形，仿真程序计算得到其SNRout=-1.576 dB。

在相同的仿真条件下，对比采样频谱细化分数阶Fourier 变换和传统分数阶Fourier 变换两种滤波算法，输出信号信噪比，改进算法比传统算法提高了近1.41 dB。

3.3 运算量分析

利用传统FRFT 对信号滤波数值计算分三步实现：chirp 调制、卷积、再次chirp 调制，第二步的卷积可通过FFT 实现，因此一次FRFT 的运算量为FFT 加上两次chirp 相乘的运算量，约为O(Nlog2N)，为了获取最优FRFT 域u0，需要扫描阶次区间[0，2]以获得u0对应的谱峰值，一般选取扫描间隔为0.01，则整个过程需要扫描的次数为200 次，即进行200 次FRFT，所以传统FRFT 滤波算法获取最优FRFT 域u0的运算量约为O(200Nlog2N)。

改进算法的运算量包括两部分：由式（8）可知，一次CZT 计算量主要为两次FFT 和一次IFFT，加上分段解线调所需的一次FFT，总计算量约为O(4Nlog2N)。因此频谱细化估计LFM 信号调频率的计算量约为O(4Nlog2N)；根据估计出的调频率，在最佳变换阶次做分数阶傅里叶变换，运算量约为O(Nlog2N)。与传统FRFT 扫描法获取u0的运算量O(200Nlog2N)相比，改进滤波算法的运算量由传统的O(200Nlog2N)降为O(4Nlog2N)。

4 结论

传统分数阶Fourier 变换滤波算法对含噪LFM 信号滤波时，需要在在分数阶Fourier 域与阶次形成的二维平面扫描获取最佳阶次，这样需要大量的运算来寻找最佳阶次，运算效率不高，运算量较大。为了减少运算量，本文将频谱细化与分数阶Fourier 变换结合，利用分数阶Fourier 变换对线性调频信号良好的能量聚焦特性，研究了含噪线性调频信号的滤波。给出了频谱细化与分数阶Fourier变换结合的含噪LFM 信号滤波算法具体流程，并以单分量含噪LFM 信号为例，建立LFM 信号滤波仿真模型，验证本文提出的频谱细化分数阶Fourier 变换信号滤波算法的可行性与有效性。利用频谱细化FRFT 可以比传统FRFT 更有效的实现含噪LFM 信号的滤波，且相对于传统的FRFT 滤波算法运算量明显减少，速度更快，更易于工程实现。