突发事件下的医院应急资源冗余配置优化模型

万志远，刘勤明，叶春明，刘文溢

（上海理工大学管理学院，上海200093）

0 引言

应急资源冗余配置是一切应急救援活动顺利开展的必要保障，但若应急资源冗余的配置不合理，会降低医院在面临突发事件时应急救援的及时性、增加突发事件的不确定性，甚至会降低医院对应急资源的利用效率。

应急资源优化问题的研究内容一直颇多。张华等［1］探讨了改良护理应急管理系统及人力资源配置在灾害救援中的应用效果，改良了医院护理应急管理体系，实施了科学的人力资源管理；张玲等［2］考虑到突发事件的不确定性，建立了随机规划模型；潘星明等［3］建立了基于仿真智能对象（Simulation Intelligent Object，SIMIO）的医院应急系统模型，模拟出突发事件下医院的应急救援过程；Xiang 等［4］提出了一个新的排队网络，以模拟病人健康状况的恶化，并提供分析解决方案和数字说明，制定了两种资源分配模型；Yang等［5］认为选择合适的分类过程并为分诊和专用实验室增加额外的容量可以显著提高急诊科（Emergency Department，ED）性能，尤其是在医生利用率很高的情况下，共享实验室通常比专用实验室为ED提供更好的支持；Su 等［6］致力于以并行方式将多个紧急资源分配给多个并发事件的挑战性问题，减少响应时间和紧急资源成本；Wen 等［7］研究了紧急医疗资源分配是用于资源优化调度的多目标优化问题。

资源冗余方面已有研究大多从冗余资源的整体出发。熊雪晨等［8］针对医院医疗系统中的资源需求变化性，认为资源冗余优化配置过程中需要有合理性；陈舒盈等［9］通过优化医疗卫生资源配置结构合理调整存量、提高医疗资源在机构内的投入产出效率、完善卫生资源配置评价体系；李晓翔等［10］研究了资源冗余与企业绩效之间不同条件下的相关性；徐莹等［11］提出了波形电路和导向按钮的资源冗余优化方法，将可靠性与转换器中的投资相协调，验证了配置策略的有效性；Cheng等［12］提出了一种基于六角锥冗余配置的单轴回旋调制捷联惯导系统（Strapdown Inertial Navigation System，SINS）方式，建立了多指标约束冗余配置的优化准则，并设计了六边形金字塔配置方案；龙婷等［13］研究了企业内部存在的冗余资源环境对企业投资和战略创新的影响调度作用。由于资源冗余方法的使用导致模型的拟态空间变大，寻优算法的求解效率需要增加，为此，何盼等［14］研究了基于相邻空间解析的模因算法。

效用理论的研究方向各有不同，李宗活等［15］引入双方风险分均的效用函数，建立了双方效益对称下的风险分均模型；Bayrak 等［16］提出了一种风险决策的新模型，该模型为经验观察到的偏好逆转提供了解释，其核心是概率感知不精确的结合，这是由于个体对数值概率的模糊理解而产生的；袁竞峰等［17］结合社会期望上的效用理论，建立了以风险决策为主的效用模型。

已有的资源冗余相关研究很少涉及突发事件下的应急资源冗余，突发事件发生前，应急资源的冗余预备必不可少，医院在正常运转的过程中，必定会出现一定量的资源冗余。本文从应急救援资源预先配置的角度出发，将应急资源冗余进行定义并分类，引入效用函数，建立突发事件下的医院应急资源冗余配置优化模型，将粒子群算法（Particle Swarm Optimization，PSO）和常用来求解效用函数的序列二次规划（Sequential Quadratic Programming，SQP）方法相结合对模型进行寻优求解，并通过一次案例分析得出研究结果。

1 模型建立

1.1 医院应急资源冗余的效用体现

由Hermann的灾难模型［18］可知，突发事件带来生命危险、决策时间紧和未知意外。应急资源冗余对突发事件下医院应急的效用可能体现在以下三点：

1）拯救生命、应急救援。应急资源冗余有助于医院拥有足够的空间去适应突发事件场景的变化，维持医院应急工作的顺利进行，即使在灾情严重的情况下，应急资源冗余完善的医院仍然能够较大程度地保障病人的生命安全。

2）灵活救援、短时间应急决策。应急资源冗余给予应急人员和医院各部门之间主动性和灵活性，突发事件发生之后，拥有较多应急资源冗余的医院中低层应急管理者能在紧急情况下灵活响应救援活动和自行做出决策，高层应急管理者面对海量的细节信息时就可以减少决策压力，集中精力进行关键性应急决策。

3）面对意外情况和紧急调度，及时完善应急体系。突发事件下应急救援活动的同时，医院可以同时审视自身的不足，及时调度应急资源，应急资源冗余能够帮助医院在临时调度过程中支持所带来的风险和意外，减少资源约束。

1.2 医院应急资源冗余及分类

本文将医院应急资源冗余定义为医院为了保障突发事件下应急救援的缓冲资源，其分类及内容表述如表1。

效用理论是管理者进行决策时使用的一种理论。突发事件下医院应急资源冗余配置优化的系统效用，即医院应急管理者对应急资源冗余产生突发事件发生时应急救援效用水平的满意度，就像消费者对商品消费的满意度。

表1 医院应急资源冗余的分类及内容Tab.1 Classification and contents of hospital emergency resource redundancy

基于突发事件下医院应急救援管理的特性，本文将医院应急资源冗余配置优化中的效用和边际效用定义为：效用表示为医院应急救援活动中，在使用应急资源（人力、物力、财力、信息）后对医院应急效用水平的满意度（即效用值）；边际效用表示医院应急救援活动中，单位应急资源冗余量使用后得到的效用值增加度。

1.3 效用函数的确定

本文选取人力保障资源冗余x1、社会保障资源冗余x2、物质保障资源冗余x3和信息保障资源冗余x4作为模型的决策变量。结合已确定的医院应急资源冗余分类，假设影响医院应急水平质量的应急资源冗余类型为S，对第i 类应急资源冗余的投入总量为xi，应急效用水平为P(xi)。在突发事件下的应急环境中，应急资源冗余可看作一种特殊而昂贵的商品，其消费应符合边际规律，即有：

边际效用的函数曲线如图1所示。

其效用函数为：

对应边际效用函数为：

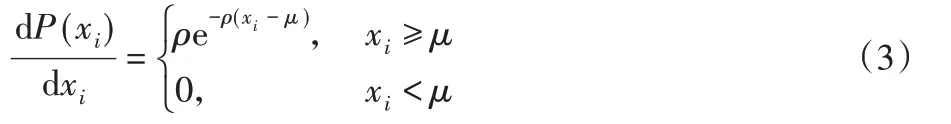
针对上述公式，引入两个变量，xmax与xmin：xmax表示医院对于应急资源冗余量的最大量值，当医院存在的应急资源冗余大于xmax时，效用值不会再增加；xmin表示安应急资源冗余量的最小量值，当医院存在的应急资源冗余小于xmin时，效用值为0。

随着xi的增加，P(xi)的值会逐步增加，且越来越趋近于1。再设置参数ε，ε是无穷小的一个值，当函数值大于或等于1-ε时，令P(xi)=1。

参数ρ 与μ 的求解过程如下：设当资源冗余为xmax时，P(xi)=1-ε；当资源冗余为xmin时，P(xi)=0。

解得：

1.4 医院应急资源冗余配置模型的建立

在上述效用函数确定后的基础上，综合资源配置优化理论，建立医院应急资源冗余配置优化模型。

当应急资源冗余的量值不变时，将其总效用值作为目标函数。记此函数的总效用为Y，则：

其中，ωi指各变量之间的加权比重，且

P(xi)和xi分别表示第i 类应急资源冗余的资源效用值和其对应的变量值。

由于医院存在的应急资源冗余总量的值是一定的，即：

其中，B表示医院储存应急资源冗余量的最大值。

根据柯布-道格拉斯函数常表示的函数关系，医院的合理应急程度可以用F(x1，x2，…，xi)表示为：

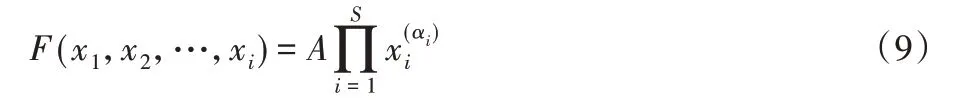
其中：A 为医院医疗技术水平系数；x1，x2，…，xi为医院各决策变量的投入；αi表示i 个决策变量之间的重要性系数，且α1+α2+…+αi=1。

医院的救援需要在一定的合理应急程度下进行，故：

其中，W为医院应急救援必须要有的最低合理应急程度。

1.5 模型最优解的必要条件

对于上述模型中的目标函数，使用拉格朗日乘数函数则可以表示为：

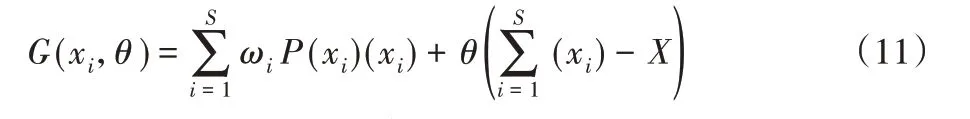
G(xi，θ)取极值的必要条件为：

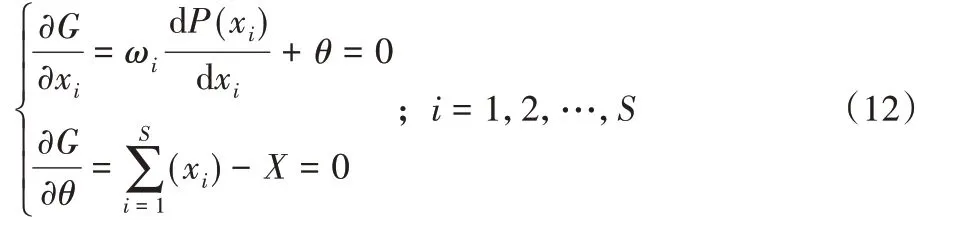
由此，得到模型最优解的必要条件为：

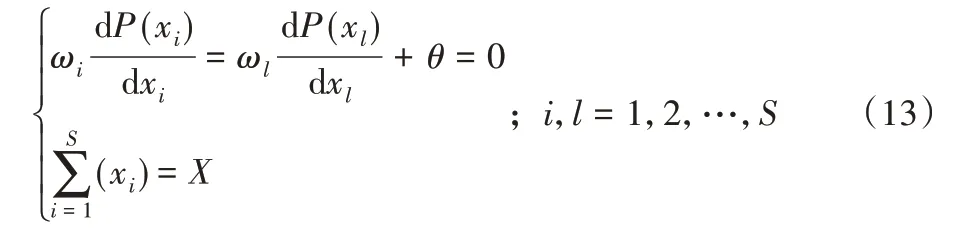
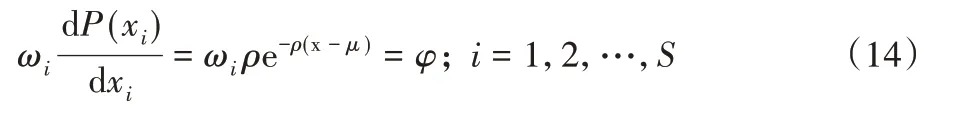
则有：

式（13）中，若记：

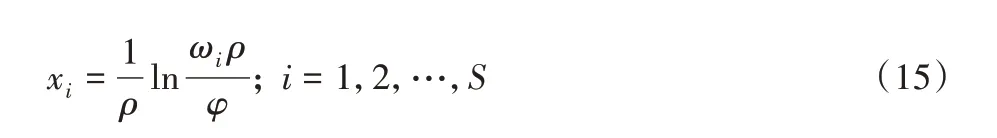
式（15）表明，当xi＞0 时，有ωiρ ＞φ。因此，医院只需对所有ωiρ ＞φ 的应急资源进行投入。记满足该条件的资源冗余类型有I个（所有资源冗余类型的重要程度已按照ωiρ由大至小进行排序），则模型最优解的必然条件式（15）等价于：

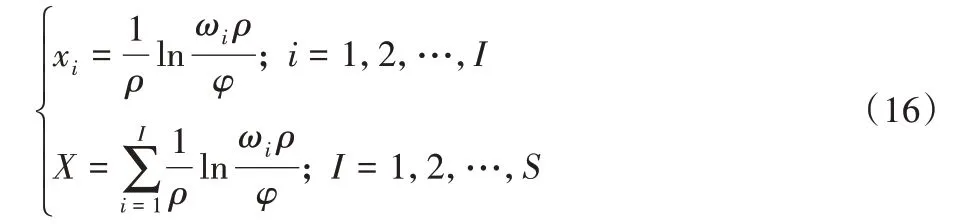
此模型属于非线性规划问题，主要特点是在求解过程中变量较多，非线性函数具有复杂性，突发事件下应急资源需求波动具有随机变化性。这样的特点使得求解难度偏高，普通的数学寻优无法很好地进行求解。本文运用拉朗日方法与KKT（Karush-Kuhn-Tucker）条件，将粒子群算法和常用来求解效用函数的序列二次规划法相结合，通过粒子群算法进行全局搜索，用序列二次规划法进行局部寻优，以此求得最优解。

2 模型求解

2.1 需求波动状态下PSO的全局寻优

PSO 操作过程较简单，且可以并行搜索寻优。用PSO 求解寻优时，首先需要初始化随机粒子，经过每一次的搜索，粒子群需要追寻2 个值来更新自己的位置和速度，个体极值和全 局 极 值 分 别 用Pi=[Pi1，Pi2，…，Pid，…，PiD]和Pg=[Pg1，Pg2，…，Pgd，…，PgD]表示。

具体迭代公式如下：

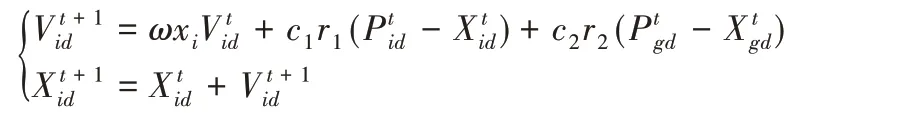
式中：Xi=[Xi1，Xi2，…，Xid，…，XiD］是指第i 个粒子在其求解集合内的所在位置，Vi=[Vi1，Vi2，…，Vid，…，ViD]是指第i个粒子其求解集合内的运行速度；ω 为惯性权重系数；c1和c2为常量，表示正的学习因子；r1、r2为0到1之间均匀分布的随机数。

而在求解过程中，粒子的速度却对全局收敛性存在着极大的影响，当求解过程中无法控制和约束粒子时，就会拖慢后期的求解，使得其求解结果的最优值不够完全。

2.2 函数梯度下降方向的SQP局部寻优

在用SQP 方法对模型进行求解时，首先需要求出每一个迭代的值，然后将其作为寻优的点，沿着该点搜索，直到逼近最终的解。

在求解非线性化的函数问题时，虽然SQP方法收敛快、求解效率较高，但其初始值的设定对求解效率和准确度有着较大的影响，初始值设定需谨慎合理。

2.3 PSO-SQP算法步骤

PSO 算法与SQP 方法的结合，避免了两者缺点的同时又有着较好的优势互补。

其主要思路是：首先，通过PSO 算法迭代搜索，当其2 次寻优的值小于规定的值时，可用其作为PSO-SQP 算法的初始值；然后，通过最大效用函数和模型中的约束建立一个适应度函数；最后，求解此函数，从而不断获取下一个迭代值，直至求得最优解。

算法具体操作及改进如下：

步骤1 设定权重系数、初始值、变量和学习因子等参数。

步骤2 初始化随机产生一定数量的粒子种群。

步骤3 采用PSO 算法进行一定次数的寻优计算，得到最优值及其变量X。

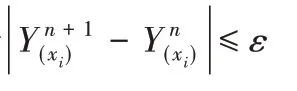
步骤5 设定xi为SQP方法的初始值。

步骤6 使用SQP 方法进行局部搜索优化并求解，从而获得Y(xSQP)的值作为其最优解，以及其对应的变量xSQP。

步骤7 判断优化计算的最终值，取2种算法的最小值为最优解，即对Y(xi)和Y(xSQP)的大小进行比较，得到最终解值。

3 算例与分析

3.1 算例描述

某医院某年的应急资源冗余总量为392 万元，其中人力保障资源冗余为92万元，社会保障资源冗余为100万元，物质保障资源冗余为105 万元，信息保障资源冗余为95 万元。突发事件下医院的合理应急度达到95 才可以达到应急救援活动的相关要求，各类参数的具体数值见表2。

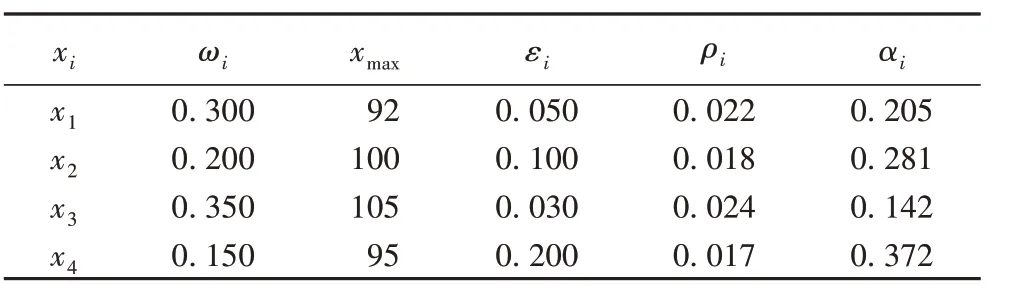
表2 应急资源冗余模型相关参数Tab.2 Related parameters of emergency resource redundancy model

3.2 算例分析

在CPU 为3.4 GHz、内存为4 GB 的计算机上，使用Matlab R2017a 编程求解，实现PSO-SQP 算法优化，设粒子群算法的种群规模为200，惯性权重取值0.729 8，两个学习因子都取值为1.494 45，运行程序30 次，求解时间都在11.401 547～11.894 152 s，说明其求解的结果和时间都具有较高的稳定性。PSO-SQP 算法适应度函数的关系变化曲线如图2所示。

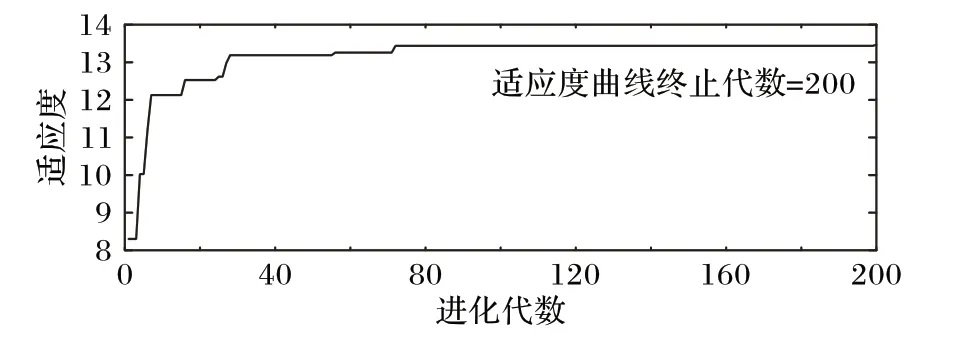
图2 PSO-SQP算法的适应度曲线Fig.2 Fitness curve of PSO-SQP algorithm

根据上述参数进行计算，可以得出该医院模型的应急总效用值Y为0.876，合理应急度为97.118。最终获得的应急资源 冗 余 量 配 置 情 况 为：xT=[101.187，117.352，162.216，70.245]，此时总效用为0.907，与优化之前相比提高了1.48%，医院的应急合理度为99.579。表3 列出了模型的优化前后结果数据。

1）人力保障资源冗余：人力保障资源冗余的量与之前相比，由92万元增加至101.187万元，表示该医院人力保障资源冗余的量偏小，需要增加。研究调查结果发现，应急救援主要依靠人力保障资源，在确保医院及时应对突发事件的能力下，该医院应增加人力保障资源冗余的投入量，提升医护人员等人力保障资源冗余的质量水平，以提高医院系统的应急效用值。

表3 医院应急资源冗余模型优化前后结果对比Tab.3 Result comparison of hospital emergency resource redundancy model before and after optimization

2）社会保障资源冗余：该医院应增加社会保障资源的投入，将社会保障资源冗余从100万元增加至117.352万元。调查显示，虽然该医院有社会保障资源冗余，但是突发事件的严重性可能导致此种资源的不足，应适量增加。

3）物质保障资源冗余：该医院的物质保障资源冗余的量投入过少，需要增加，应该由105 万元增加至132.216 万元。良好的物质保障基础能帮助医院在面对突发事件时提高应急水平，使得医院的应急救援活动能够快速有效地进行。

4）信息保障资源冗余：该医院的信息保障资源冗余的量偏多，需要由95 万元减少至78.245 万元。调查结果显示，该医院为了增加突发事件反应调度功能，投入了偏多的信息管理系统构建和应急知识培训课程。然而由于大量的培训在后续时段内缺乏对受培训医护人员的知识查验，使得许多应急人员没有真正具备正确的应急能力，让医院的应急管理存在疏漏。因此，该医院应提高应急人员的综合能力，以及多引进应急管理高水平人才，提升管理人员的综合水平和能力。

另外，不同医院的应急水平不同，如表4 所示，其应急合理度也不同，为了进一步验证模型的有效性以及分析不同类型资源冗余的优势，通过调查，得出的不同医院的资源冗余需求如表5所示。

表4 医院应急水平对比Tab.4 Comparison of hospital emergency levels

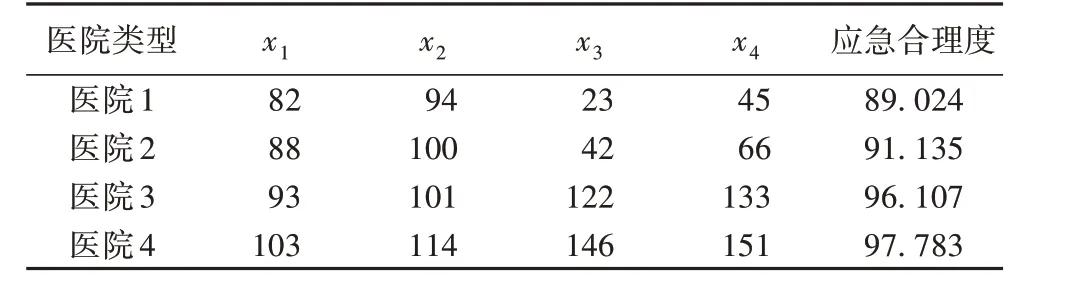
表5 几种医院的应急资源冗余对比Tab.5 Comparison of emergency resource redundancy in several types of hospitals

可以看出，对于应急水平为低和中的中小型医院来说，其冗余资源主要在于人力保障资源和物质保障资源，社会保障资源与信息保障资源的适用性较低；相反，对于应急水平高的一些大型医院来说，社会保障资源与信息保障资源的重要性呈直线上升。

这是因为大型医院在突发事件发生的时候，承担的救援任务较重，信息保障资源的及时供应显得尤为重要，应急管理制度的完善亦需要信息保障资源提供强有力的支撑；而对于小型医院来说，人力和物力是最直接的应急手段，所以这两种资源冗余的妥善完备更为重要。图3 为上述几种类型医院优化前后的应急合理度数值。两条曲线所构成的区域代表着优化的效果，面积越大效果越明显。

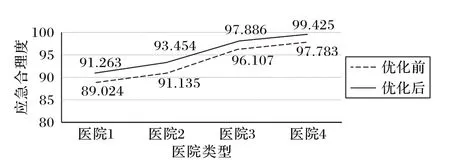
图3 几种类型医院应急合理度优化前后对比Fig.3 Comparison of emergency rationality of several types of hospitals before and after optimization

4 结语

本文首先从应急救援资源预先配置的角度出发，阐述了医院应急资源冗余效用所体现的三个方面，将应急资源冗余进行定义并分类；之后引入效用函数，建立了突发事件下的医院应急资源冗余配置优化模型，将常用来求解效用函数的序列二次规划方法和粒子群算法结合对模型进行寻优求解；最后通过一次案例分析，将某医院的应急资源冗余进行了合理优化配置，优化后的总效用水平提升了1.48%，验证了突发事件下应急资源冗余配置优化的合理性和有效性。

然而本文的应急资源冗余是医院为了保证突发事件下应急救援活动的合理进行而留存的“预备资源”，应急资源冗余的总量如果太多，就会使得医院的运行成本偏大，所以在确保医院应急水平合理化的同时，怎样减少医院的应急资源冗余量，是我们以后的研究方向。