基于DoG检测图像特征点的快速二进制描述子
刘 凯,汪 侃,杨晓梅,郑秀娟
(四川大学 电气工程学院,四川 成都 610065)
1 引 言
图像的局部特征独特性好,对光照、旋转、视角变化等图像转换都具有不变性,因此被广泛应用于图像拼接、目标识别、目标跟踪和图像检索等领域[1-6]。尤其在大场景的三维重建[7-8]中,优秀的特征描述能帮助我们以极高的效率重建出精细的三维模型。局部特征的提取分为两个步骤:关键点检测[9]和描述子生成[10-11],本文主要讨论描述子的设计。
关键点描述子按照描述子的表现方式分为浮点数描述子和二进制描述子。浮点数描述子中最典型的方法是尺度不变特征变换(Scale Invariant Feature Transform,SIFT)[12]。在对局部描述子的性能评估后,Mikolajczyk和Schmid[10]提出SIFT描述子具有最好的鲁棒性和独特性。但是SIFT描述子生成复杂,匹配效率低下,因此许多学者对SIFT算法进行了改进和扩展。Bay等[13]提出利用关键点邻域的小波响应来生成64维描述子;Ke等[14]和颜雪军等[15]提出用主成分分析的方法对SIFT梯度向量块进行降维;Tola等[16]和曾峦等[17]通过提出新的分块策略构建特征描述子,降低了描述子运算复杂度;耿庆田等[18]提出在边缘检测出的感兴趣区域上构建全局SIFT组合特征向量,通过减少冗余极值点来提高SIFT算法的效率;唐永鹤等[19]在Schmid等[20]研究的基础上提出了基于灰度差分不变量区域统计直方图的算法来提高特征描述子的稳定性。
浮点数描述子虽然有良好的性能,但是采用统计直方图的方法计算量大,描述子占用存储容量多,匹配时间复杂度高。而二进制描述子采用比特位的存储方式,占用容量小,同时,其通过计算汉明距离来匹配。汉明距离通过异或运算实现,计算效率极高,经典的二进制描述子主要包括:二值鲁棒独立单元特征(Binary Robust Independent Elementary Features,BRIEF)[21]、ORB[22]、二值鲁棒不变尺度关键点(Binary Robust Invariant Scalable Keypoints,BRISK)[23]、快速描述神经元类关键点(Fast Retina Keypoint,FREAK)[24]。上述二进制描述子均是基于灰度比较的描述子,随着近年来机器学习方法的高速发展,越来越多的学者通过机器学习的方法来为特征点提取二进制描述子。在有监督学习中, Trzcinski等[25]通过训练将几个弱分类器组成强分类器,进而将图像特征投影为二值结果构成描述子;Balntas等[26]基于线性判别分析离线训练不相关的二进制测试点对,在线训练特征子集块,提高了机器学习中二进制描述子提取的速度。在无监督学习中,Lin等[27]提出DeepBit方法来学习生成紧凑的二进制描述子;Zieba等[28]提出新的正则化方法,并应用到对抗生成网络上生成在图像匹配和图像检索表现优异的二进制描述子;Duan等[29]应用KAEs网络在深度学习框架下共同学习参数和二值化功能。然而,这些通过机器学习提取二进制描述符的效率要远低于传统描述符的提取效率。
在上述描述子的基础上,本文设计了一种时间复杂度低、鲁棒性更好的二进制描述子。首先,结合传统二进制描述子采样模式的优点,本文提出了新的采样模式,新采样模式的同心圆半径和采样点的滤波半径均与尺度关联,且采样点采用均值滤波;然后,根据特征点主方向,我们将采样模式中各采样点旋转到特定位置;接着,我们选择最优的最小相关点对比较模式,该模式通过机器学习的方法从采样模式中选取独特性最好、相关性最低的128对点对;最后,在点对灰度值比较的基础上,我们添加梯度绝对值和比较来构建二进制描述子。
2 生成二进制描述子
2.1 设计采样模式
BRIEF特征点的采样区域是以特征点为中心的一个的邻域块,论文作者在邻域块中随机选取点对进行二进制编码;BRISK以特征点为中心,构建不同的同心圆,在每个圆上获取一定数目的等间隔采样点;FREAK算法的采样模式接近于人眼视网膜接收图像信息的采样模型,在离中心点近的采样点密度高,远离中心点的采样点密度低;惠国保等[30]提出采样点密度和平滑范围重叠度均对采样模式有影响,在中心集中度为78%,重叠度为22%时能使描述子的独特性最大化。本文分析了BRIEF,BRISK和FREAK的采样模式特点,在其基础上提出了新的采样模式,如图1所示。
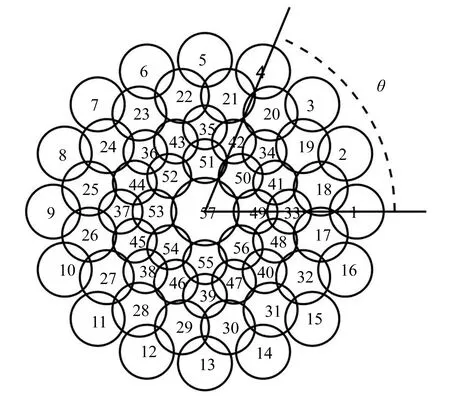
图1 采样模式示意图Fig.1 Sampling pattern
图1是特征点组内尺度σ=1.6时的采样模式示意图,其中每个圆形代表采样点的平滑范围。采样模式共计5层,即有5个以特征点为中心的同心圆,同心圆的半径分别为3σ,4.5σ,5σ,7σ,9σ。其中中心点的平滑半径为2σ。采样模式内3层的每个同心圆上均匀分布着8个采样点,每个采样点的平滑半径为1.3σ。各采样点在坐标系下的位置如公式(1)所示:
(1)
其中:同心圆的半径r=3σ,4.5σ,5σ,采样点的序号k=0,1,…,7,采样模式的层数t=1,2,3,p(t)函数在t为奇时取0,t为偶时取1,θ表示特征点主方向。
采样模式外2层的每个同心圆上均匀分布着16个采样点,每个采样点的平滑半径为1.6σ。各采样点在图像坐标系下的位置如公式(2)所示:
(2)
其中:同心圆的半径r=7σ,9σ,采样点的序号k=0,1,…,15,采样模式的层数t=4,5,q(t)函数在t为奇时取1,t为偶时取0,θ表示特征点主方向。
本文提出的采样模式与BRIEF,BRISK和FREAK的有很大不同。BRIEF在方形区域内检测随机点对的响应值;BRISK的采样模式有4层,每层上均匀分布着10,14,15和20个采样点,采样点平滑范围彼此独立,没有重叠;FREAK采样模式有7层,每层上均匀分布着6个采样点,采样点平滑范围高度重叠,产生大量冗余信息。本文提出的采样模式是在BRISK采样模式的基础上推广而来。首先,采样模式中同心圆的半径和采样点平滑范围均和特征点的尺度关联以确保采样的尺度不变性,其次,相较于BRISK采样模式,本文提出的采样模式更密集,各个采样点之间不存在空隙,更能充分利用特征点周围的邻域,而且本文对采样点采用均值滤波替代BRISK中采用的高斯滤波,在减小计算量的同时,使相邻的采样点存在部分重叠,有利于提高描述子的独特性,最后,采样模式根据特征点尺度最小值选取平滑范围,确保所有采样点的平滑范围在3×3以上,避免了BRISK采样模式内圈采样点平滑范围太小的缺陷。因此,本文提出的采样模式相较于BRISK采样模式有更大优势。
2.2 特征方向
为保证描述子的旋转不变性,需要将特征点周围的区域旋转到主方向上去,对采样模式中的每个采样点编号如图1所示。解决旋转不变性主要包括以下两个步骤:
(1)采用SIFT的主方向估计方法得到特征点的主方向θ;
(2)将采样点1和特征点的连线方向与主方向θ对齐。
将特征点周围整个区域旋转到主方向的代价比较高,为减少运算量,本文仅将57个采样点旋转到相应位置。首先,在特征点组内尺度为1.6,主方向为0时,建立查找表存储57个采样点的横、纵坐标,然后对组内尺度σ、主方向θ、编号n的采样点,按如下公式计算其横坐标x与纵坐标y:
(3)
其中X,Y是存储表中编号为n的采样点的横、纵坐标。
2.3 特征描述
参考局部二值模式[31]与ORB,本文提出以下三种采样点对模式方案:
(1)中心点比较模式(Center Comparison Pattern,CCP),即同心圆上任意一点与中心点组成点对;
(2)中心对称比较模式(Centrosymmetric Comparison Pattern,CSCP),即同心圆上一点与其关于中心点的对称点组成点对;
(3)最小相关点对模式(Minimum Correlation Pattern,MCP),其算法步骤如下:
a.从ImageNet Large Scale Visual Recognition Challenge 2012测试集数据集中选取1 000张图片共提取K=276 696个特征点。对于每个特征点,从其周围邻域的57个采样点中选取两个采样点(xp,xq)组成点对进行灰度值大小比较。点对的选取如公式(4)所示:
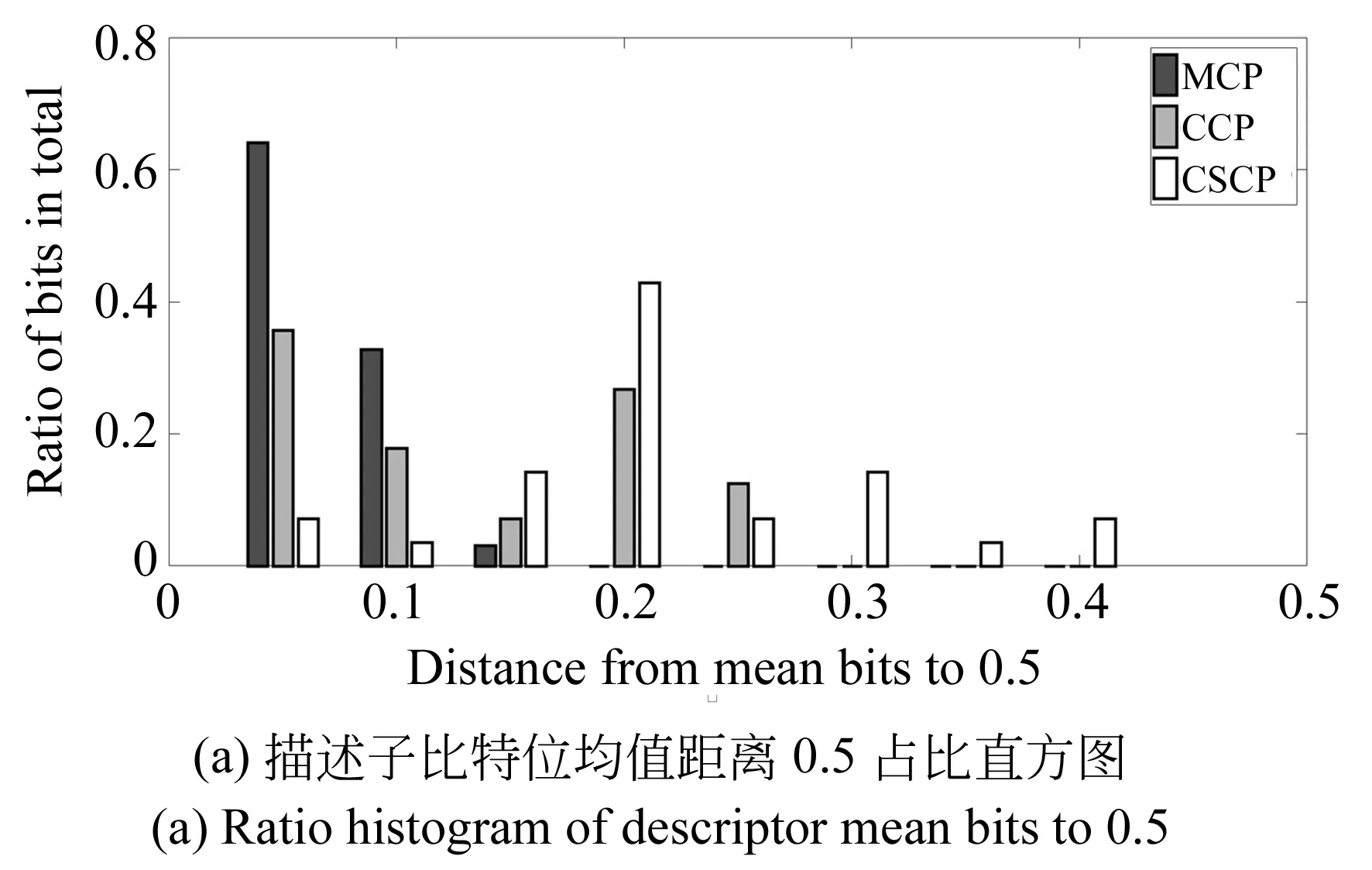
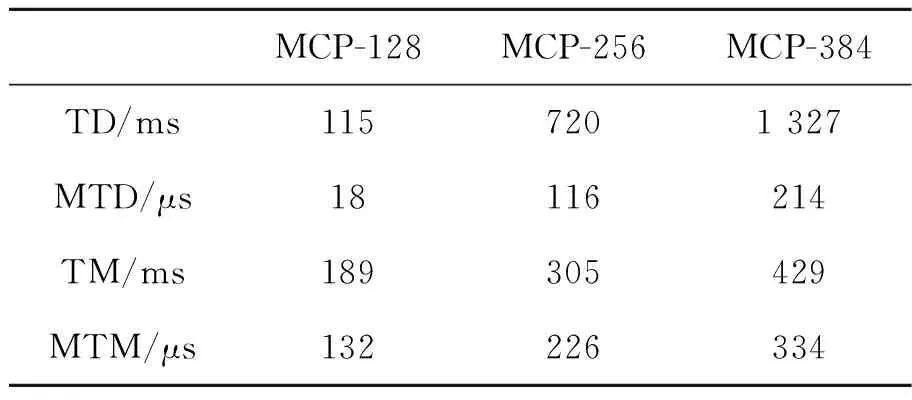
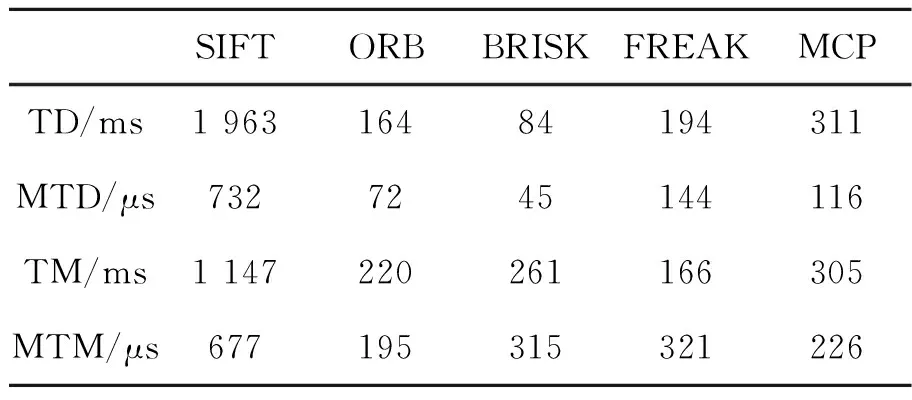
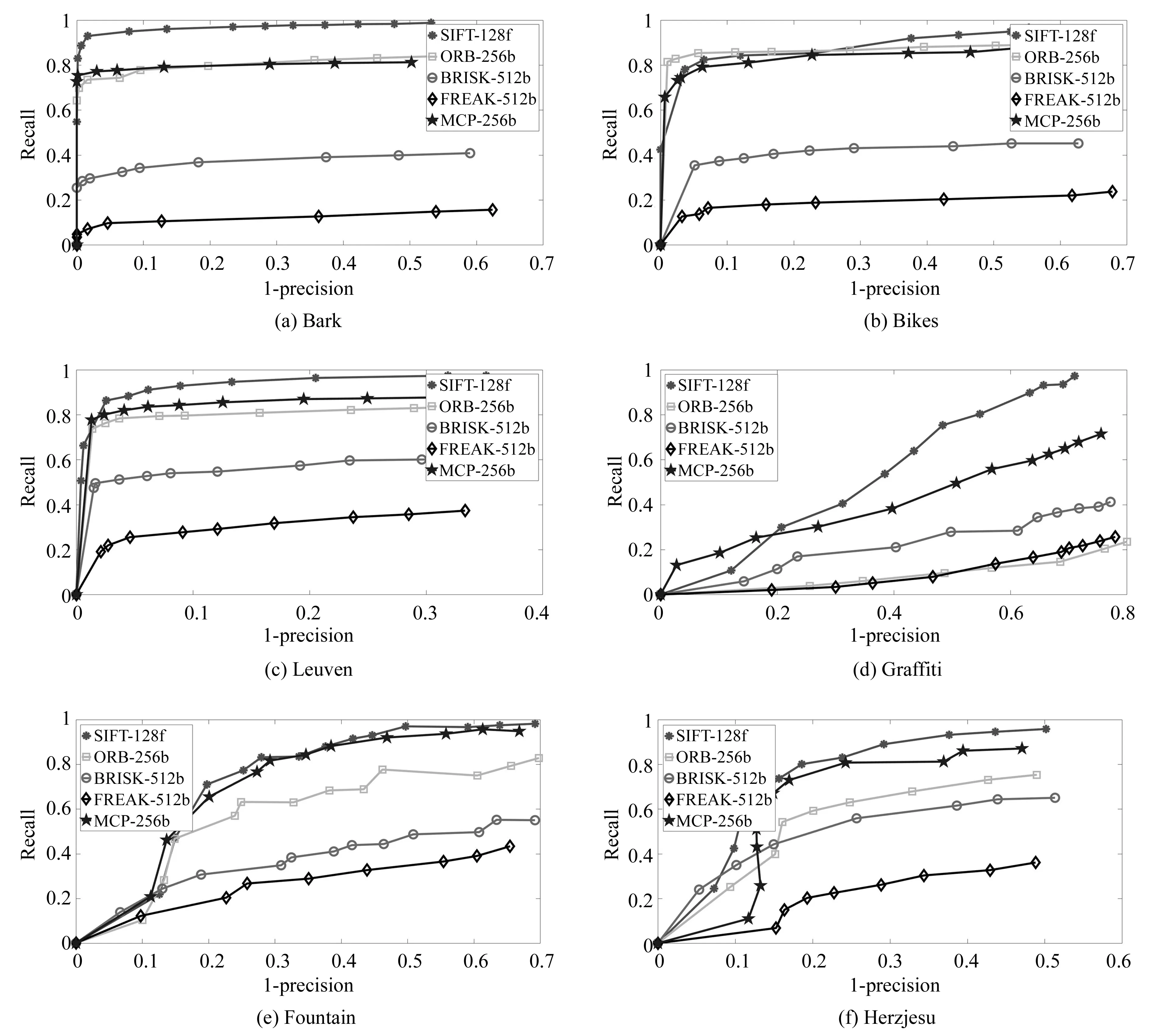
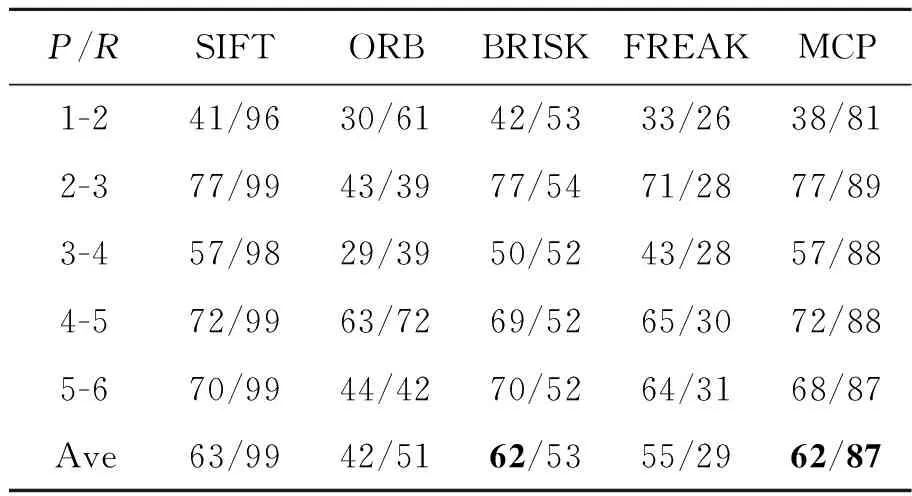
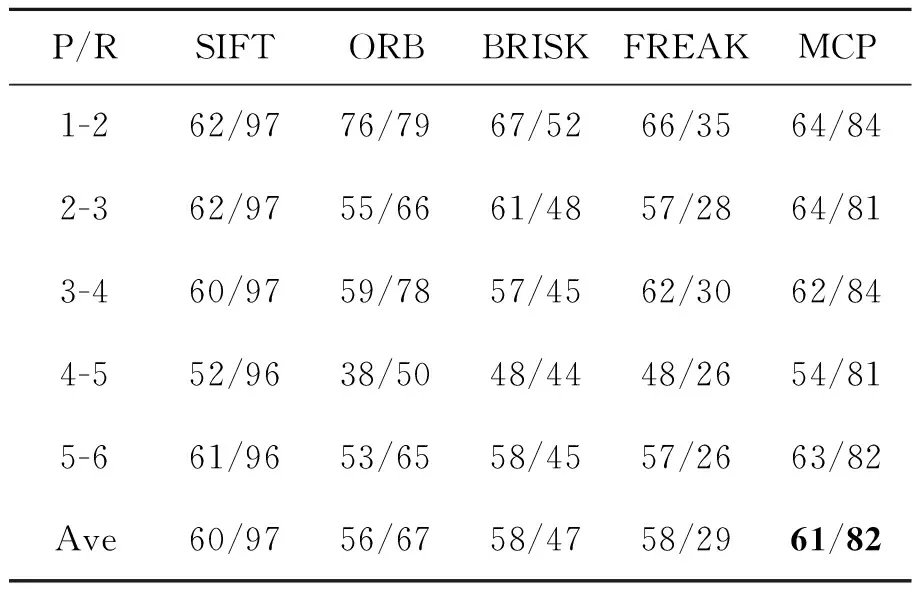
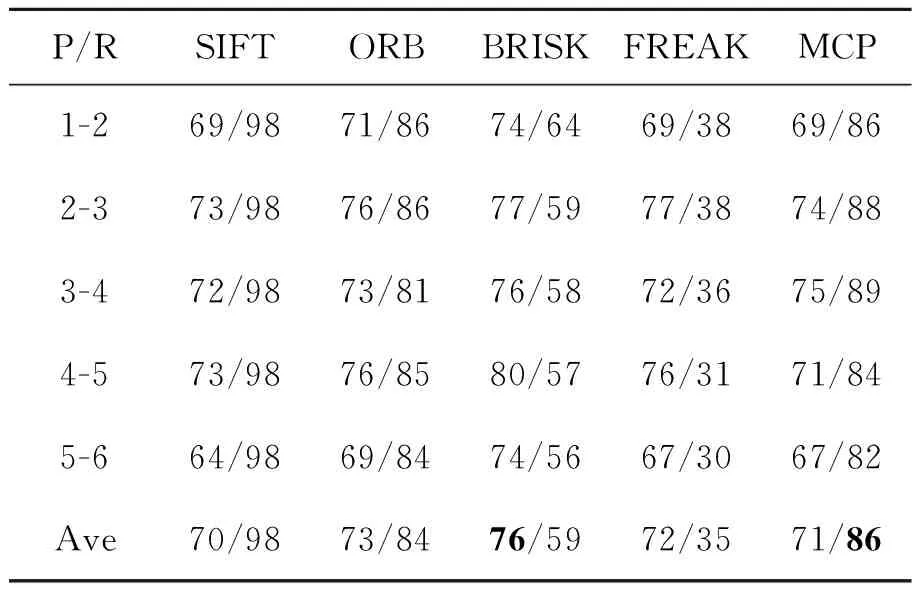
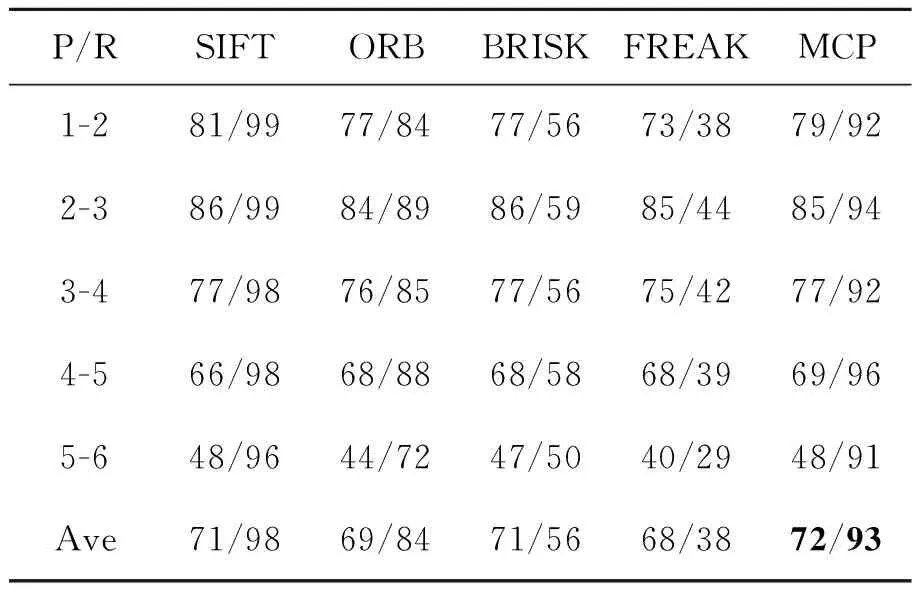
A={(xp,xq)|1≤p<57∧p (4) 对于每个特征点有M=1 596个二进制测试结果,将K个特征点的测试结果排列成K×M的矩阵; b.令S为测试结果矩阵中列的集合,计算S中每列均值,从中选取均值为0.5的列加入集R,对于S中剩下的列,从中挑选出均值与0.5的绝对距离在0.1以内的列,计算其与集R中每列的相关性,若均小于一定的阈值则添加到集R中,直到R中有128列; c.确定集R中每列所对应的点对。经选择后的最小相关点对如图2所示,其中每条线段连接的两个采样点为一对点对。 图2 采样点对示意图Fig.2 Sampling point pairs 从测试集数据集中另选130幅图片共提取32 264个特征点对三种采样点对模式的优劣进行比较,结果如图3所示。 图3 描述子均值、特征值测试结果图Fig.3 Results of descriptor mean value and eigenvalues 从图3(a)中可以看出,MCP生成的描述子每个比特位均值靠近0.5,表明每个比特位方差靠近最大样本方差0.25,这使得描述子不同比特位之间有着较大的区分度,即描述子独特性较好。而CCP描述子比特位均值分布较为宽泛,CSCP描述子比特位均值分布离0.5较远,因此这两种模式生成的描述子比特位方差较小,描述子之间区分性较差,容易造成误匹、错匹。图3(b)是主成分分析后,三种点对模式描述子最大的20个特征值分布情况。MCP和CCP描述子的初始特征值较大,表明两种描述子各比特位之间的相关性较弱,而CSCP描述子的初始特征值较小,描述子各比特位之间的相关性强,即各比特位之间的采样结果相互影响。综上比较可知,MCP描述子每个比特位均值和方差为最大,不同比特位之间的相关性弱,描述子独特性最好,区分度最高,故以下实验中的描述子均采用MCP描述子。 传统的二进制描述子采样点之间仅仅比较灰度值信息,比较结果受噪声的影响较大。受文献[18,19]的启发,本文在采样点灰度值比较的基础上,增添新的灰度差分不变量比较,如公式(5)所示: (5) 其中:V[0]表示该采样点的灰度值,V[1]表示梯度绝对值和,V[2]表示二次梯度和。同时,为减少噪声的影响,用采样点平滑区域所有像素点V[i]和的均值代表采样点的V[i]值: (6) 其中:Rn表示编号n的采样点的平滑区域,N表示平滑区域像素点的个数。二进制编码规则如下公式所示: (7) 其中s(x)的表达式如下: (8) (9) (10) 本文采用牛津标准图像集和Fountain,Herzjesu数据集评估特征描述子。牛津标准图像集下共有8个子集,涵盖有不同程度的几何和光度转换,包括:图像旋转、尺度变化、光照亮度变化、图像模糊、视角变化和JPEG压缩。Fountain和Herzjesu数据集主要测试小角度视角变换和非平面几何的影响。本文采用的评估标准是Mikolajczyk和Schmid提出的查全率(Recall): (11) 和错误率(1-precision): (12) 其中:#correctmatches是在匹配成功的点对#matches中通过随机抽样一致性确定的正确匹配的点对数,#pointcorrespondence是所有能匹配上的点对数,在实验中取SIFT描述子最近邻匹配(即距离阈值α=1.0)后通过随机抽样一致性确定的点对数。本文在Intel(R) Core(TM) i3-3240 CPU @3.40 GHz双核四线程CPU的平台上,采用C++编程。 图4 不同维数MCP描述子匹配结果Fig.4 Matching results of MCP descriptors with different dimensions 二进制描述子维度对描述子性能有很大影响,描述子维度太低不能充分挖掘采样点邻域信息,而描述子维度太高会增大错匹率。本文对提出的三种MCP描述子进行图像匹配性能评估,测试图像选择为牛津标准图像集中Graffiti图像集的第一幅和第三幅图片,测试结果如图4所示。可以看出,为MCP描述子添加梯度信息后,能显著提高描述子的性能,同时,MCP-256描述子和MCP-384描述子的性能相当,即添加二次梯度信息并不能有效地提升MCP描述子性能。 三种维度描述子的实时性测试结果如表1所示,测试的数据主要包括:两幅图片所有描述子的生成时间(Time of Descriptors,TD)、平均每个描述子的生成时间(Mean Time of Descriptors,MTD)、两幅图片描述子的总匹配时间(Time of Matching,TM)、平均每个匹配的花费时间(Mean Time of Matching,MTM)。实验中两幅图片生成的描述子个数分别为2 681、3 521,匹配的总数为距离阈值α=0.95时两幅图片的匹配个数。 表1 不同维数MCP描述子实时性测试结果 Tab.1 Real-time performance of MCP descriptors with different dimensions MCP-128MCP-256MCP-384TD/ms1157201 327MTD/μs18116214TM/ms189305429MTM/μs132226334 MCP-256描述子需要计算梯度绝对值信息,从表1可以看出,其MTD比MCP-128描述子多出一个数量级,同时,由于MCP-256描述子优秀的性能增加了匹配数,MTM并没有达到MCP-128描述子的两倍。MCP-384描述子的MTD和MTM均大于MCP-256描述子,但描述子性能却没有提高。因此,在以下描述子的实时性和鲁棒性评估中,均使用MCP-256描述子。 实时性是检测二进制描述子性能的一个重要方面。实验中描述子的测试图像为Graffiti图像集中的第一幅和第三幅图片,实验给出五种描述子算法(SIFT,ORB,BRISK,FREAK和MCP)性能的测试结果,其中SIFT,ORB,BRISK和FREAK的关键点检测、描述子生成均使用OpenCV3.1.0中的封装函数,所有描述子的匹配采用暴力匹配法。实验中取20次测试结果的平均值作为测量的实际值,图像匹配的距离阈值α=0.95,测试结果如表2所示。 从表2中可以看出,二进制描述子的MTD和MTM均要小于浮点数描述子。同时,MCP描述子的MTD要大于BRISK和ORB的MTD,但小于FREAK的MTD,比SIFT的MTD小84%;MCP描述子的MTM仅略大于ORB的MTM,比SIFT的MTM小67%。 表2 不同描述子实时性测试结果 Tab.2 Real-time performance of different descriptors SIFTORBBRISKFREAKMCPTD/ms1 96316484194311MTD/μs7327245144116TM/ms1 147220261166305MTM/μs677195315321226 实验中采用DoG检测关键点,匹配测试图像选用Bark图片集(尺度+旋转变化)、Bikes图片集(模糊变化)、Leuven图片集(光照变化)、Graffiti图片集(大角度视角变化)、Fountain及Herzjesu图片集(非平面几何)中的第二张与第四张图片,测试图片如图5所示,测试结果如图6所示。在查全率-错误率曲线中,描述子匹配曲线越往上,描述子的鲁棒性越好。实验中选用的#pointcorrespondence是SIFT描述子最近邻匹配后通过随机抽样一致性筛选的匹配数。 图5 描述子鲁棒性测试图片Fig.5 Test images of descriptor robustness 参与比较的五种描述子中,SIFT是128维浮点数描述子,其他均为二进制描述子,ORB,BRISK,FREAK和MCP分别是256维、512维、512维和256维描述子。从图6中可以看出,MCP描述子的性能好于其他二进制描述子,尤其体现在视角变化(Graffiti)和非平面几何变换(Fountain,Herzjesu)上,这跟MCP描述子好的采样模式、独特的特征描述以及添加灰度差分不变量比较测试均有直接的联系。但是,二进制描述子相对于SIFT描述子仍有不足。在采用DoG检测关键点的前提下,二进制描述子在大多数图像变换下达不到SIFT描述子的高召回率。 图6 不同描述子鲁棒性测试曲线图Fig.6 Diagram of different descriptor robustness 用4种二进制描述子分别匹配Fountain图像集的第2张和第4张图片、Graffiti图像集的第4张和第5张图片,结果分别如图7、图8所示。从下面两幅图中可以看出,在非平面几何变换(Fountain)和视角变化(Graffiti)下,MCP描述子的正确匹配数要远高于其他二进制描述子。 对Bark,Bikes,Graffiti,Leuven,Ubc和Wall图片集中相邻图片两两匹配,对描述子进行鲁棒性测试。距离阈值α=0.95,P/R表示准确率/召回率,Ave表示均值。其中SIFT浮点数描述子作为基准参考不参与比较,黑色加粗部分表示该图像集下二进制描述子的最优值。比较结果如表3~表8所示。 从表3~表8可以看出,在六种图像变换中,相较于其他二进制描述子,MCP描述子的准确率、召回率在四种变换下更高。尤其在视角变化(Graffiti,Wall)下,其准确率要比其他二进制描述子高3%~5%,召回率平均要高30%以上。 图7 不同描述子的Fountain图像对匹配结果Fig.7 Matching results of different descriptors on Fountain 图8 不同描述子的Graffiti图像对匹配结果Fig.8 Matching results of different descriptors on Graffiti 表3Bark图像集描述子鲁棒性测试结果 Tab.3 Robustness results of different descriptors on Bark (%) 表4Bikes图像集描述子鲁棒性测试结果 Tab.4 Robustness results of different descriptors on Bikes (%) 表5Graffiti图像集描述子鲁棒性测试结果 Tab.5 Robustness results of different descriptors on Graffiti (%) 表6Leuven图像集描述子鲁棒性测试结果 Tab.6 Robustness results of different descriptors on Leuven (%) 表7Ubc图像集描述子鲁棒性测试结果 Tab.7 Robustness results of different descriptors on Ubc (%) 表8Wall图像集描述子鲁棒性测试结果 Tab.8 Robustness results of different descriptors on Wall (%) 选择Fountain图像集、Herzjesu图像集中的8张图片,分别用MCP描述子、SIFT描述子重建三维稀疏点云,结果如图9所示。 从图9可以看出,MCP描述子重建的稀疏点云密度SIFT描述子的相近,这跟SIFT描述子、MCP描述子的高召回率有直接的关系。但MCP描述子的重建效率要远远高于SIFT描述子。 图9 Fountain,Herzjesu三维稀疏点云Fig.9 Sparse point cloud of Fountain and Herzjesu 本文针对SIFT描述子构建时间、匹配时间长和传统二进制描述子对尺度、视角变化和非平面几何变换鲁棒性差的问题,提出了一种新的二进制描述子算法。算法优化采样模式,根据特征点主方向旋转采样点到特定位置,并选择机器学习训练后的128对独特性好、相关性低的采样点对,在传统二进制描述子灰度值比较的基础上,添加梯度绝对值和比较测试构建描述子。实验结果表明,本文提出的二进制描述子在描述子构建时间、匹配时间分别比SIFT描述子少84%,67%,在有视角变化的图像匹配上,准确率比传统的二进制描述子高3%~5%,召回率平均要高30%以上。但是本文提出的二进制描述子召回率不如SIFT描述子,下一步的工作将为提出的描述子选择合适的关键点检测器,增加描述子的匹配数总量,提高描述子的召回率。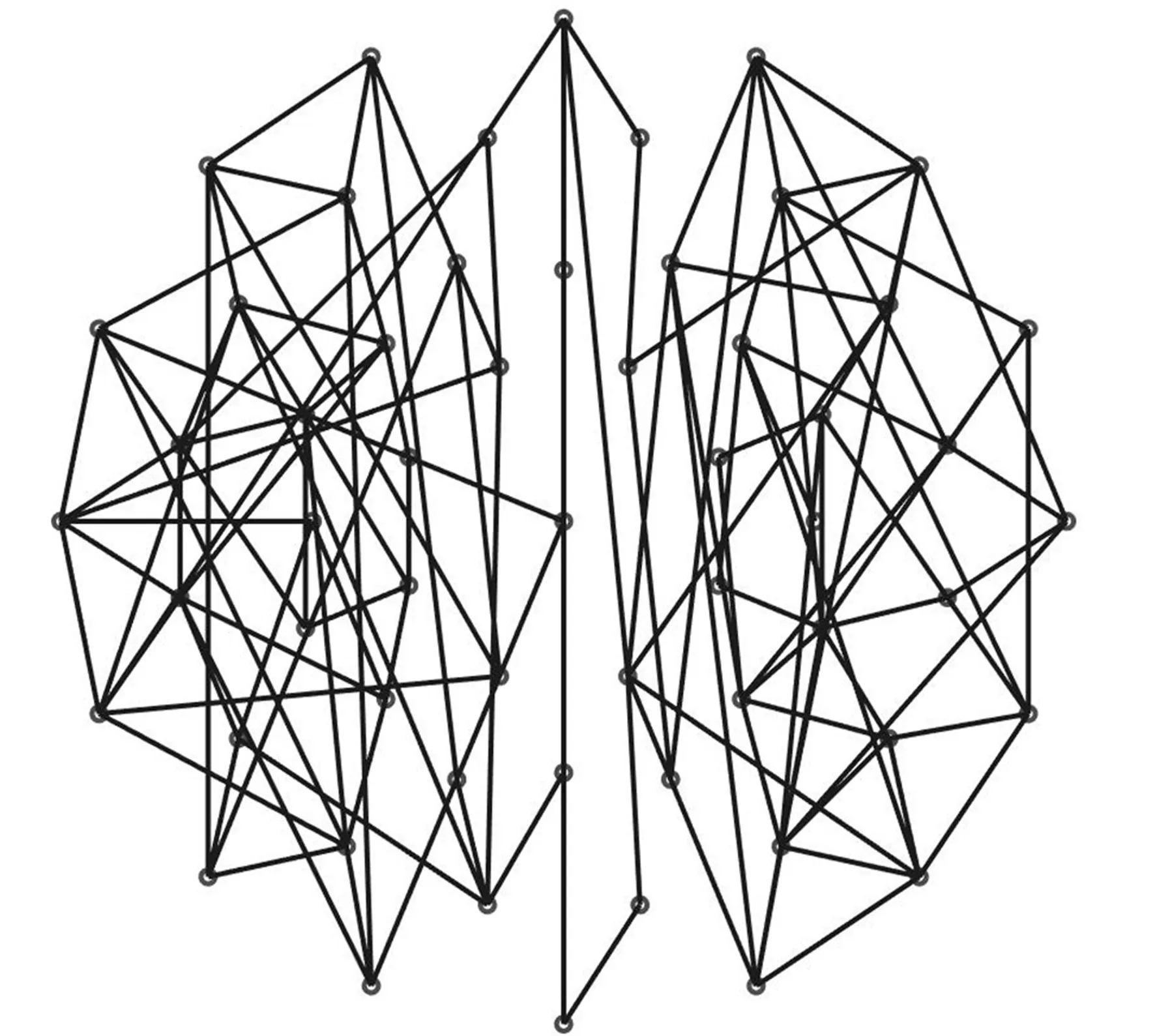

2.4 灰度差分不变量比较
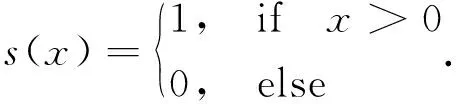
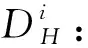
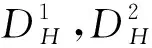
3 测量实验与结果
3.1 描述子维数评估
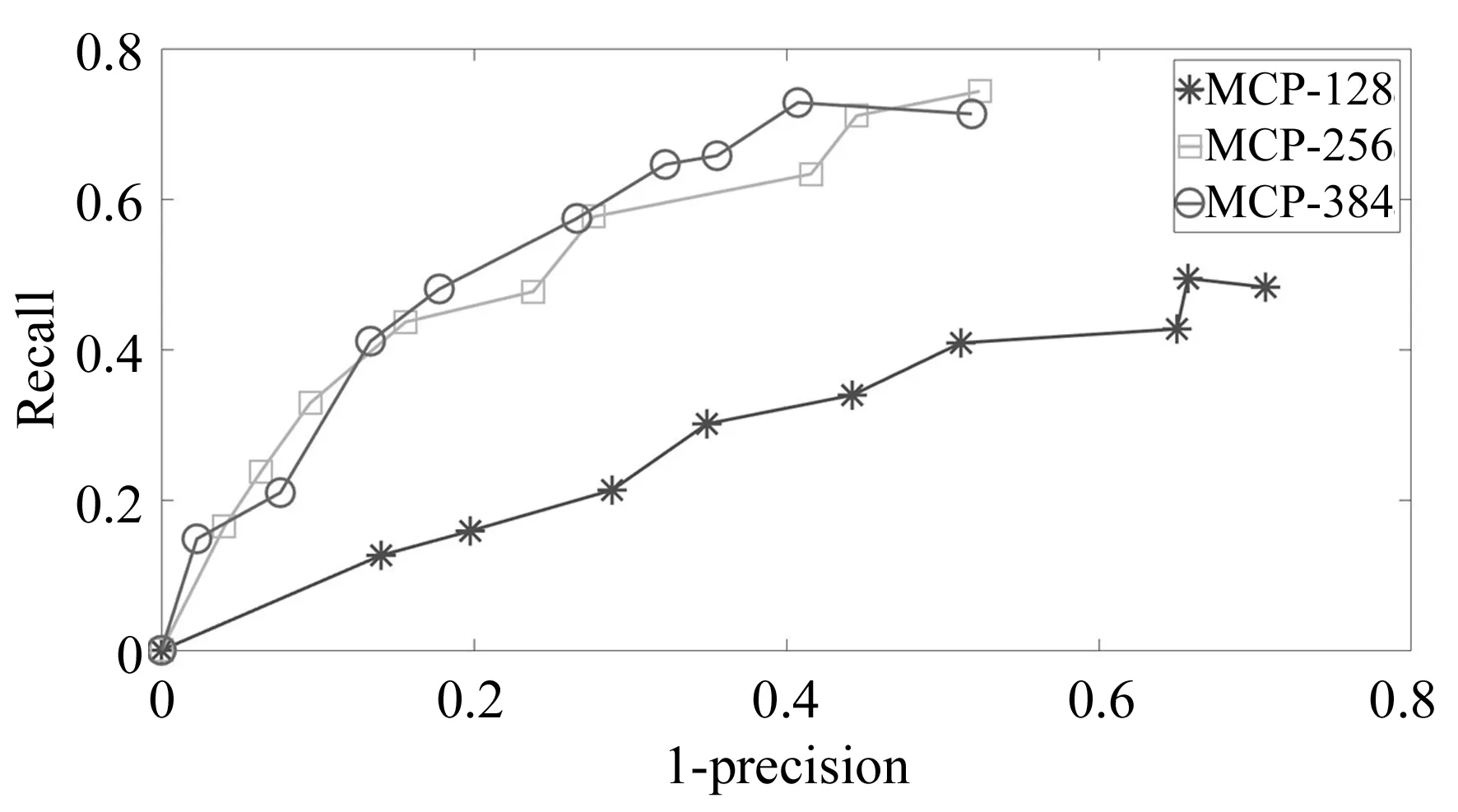
3.2 描述子实时性评估
3.3 描述子鲁棒性测试





3.4 三维重建实验


5 结 论

