引入变异算子的改进贪心和蚁群混合算法

张玉茹,王晨旸

(1.哈尔滨商业大学 计算机与信息工程学院，黑龙江 哈尔滨 150028;2.哈尔滨商业大学 黑龙江省电子商务与信息处理重点实验室，黑龙江 哈尔滨 150028)

0 引言

旅行商问题(Travelling Salesman Problem, TSP)是经典的NP(Non-deterministic Polynomial)难问题，旅行商从某个城市出发，遍历图中所有城市且不重复，最终回到出发城市，求使得经过路径最短的遍历顺序及其路径长度[1]。当图中所有城市的数量为n时，遍历图中所有城市且不重复的路径共有(n-1)条[2]。随着图中城市数量的不断增加，遍历图中所有城市且不重复的路径的数量也将以阶乘级别进行增长。目前求解TSP的算法主要包括完全算法(精确算法)和不完全算法(近似算法或启发式算法)两类。完全算法包括但不限于以下算法：①穷举搜索法，将所有情况罗列，逐个进行两两比较，该算法计算量大，但结果准确；②贪婪法，每一步都按照当前最好情况去选择，以求得最终的最优解，适合求解“单峰”问题；③动态规划法，将复杂问题进行分解后分别求解，再合并求解结果得到复杂问题的解，适合小规模问题求解；④分支定界法，通过约束边界控制搜索进程，不适合求解规模较大的问题。不完全算法包括但不限于以下算法：①插入算法，建立初始路径，不断向初始路径中插入新城市得到复杂路径，使得插入点到附近两个城市的距离最小；②最近邻算法，是贪心法的一种特殊情况，不断选取到当前城市距离最近的城市作为下一个城市；③神经网络算法，通过不断学习训练确定神经元之间的权值，使得网络能量达到最低并趋于稳定；④模拟退火算法，从初始高温出发，伴随着温度下降，利用概率的变化随机寻找全局最优解；⑤蚁群算法，每只蚂蚁随机寻找全局最优解，通过传递信息素让生成路径不断收敛，求得全局最优解。在工程实践中，不完全算法能够在较短的时间内得到一个极好的近似解，因此成为了人们研究求解TSP方法的热点之一[3]。

1 蚁群算法

蚁群算法是一种群智能启发式算法，其算法设计灵感来自于自然界中蚂蚁寻找食物过程中规划蚁群行动路径的行为。每一只蚂蚁从巢穴向四周寻找食物，在蚂蚁经过的路径上留下信息素，找到食物的蚂蚁沿着路径再返回巢穴，之后出发的蚂蚁有倾向地选择信息素浓度高的路径。随着时间的推移，最短路径上的信息素浓度越来越高，同时吸引更多的蚂蚁沿着最短路径走，形成正反馈，最终所有的蚂蚁都在最短路径上行动，实现整个蚁群的路径规划[4]。

基本蚁群算法的原理如下：在初始时刻，m只蚂蚁随机放置于n个节点中，节点与节点之间n(n-1)/2条边上的信息素初始值相等，即τi,j(0)=τ0为信息素初始值，τ0为常数。其次，蚂蚁k(k=1,2,…,m)根据式(1)计算得到的转移概率，通过轮盘赌算法随机地选择下一个节点。

(1)

式中：τij表示边(i，j)上的信息素；ηij=1/dij表示从节点i转移到节点j的期望启发式，即节点i与节点j之间距离的倒数；allowedk表示蚂蚁k下一步被允许访问的节点集合；α表示信息启发式因子，代表信息素浓度对状态转移概率计算的影响度；β表示期望启发式因子，代表期望启发式对状态转移概率计算的影响度，即节点i与节点j之间距离对状态转移概率计算的影响度。

为了让蚂蚁每个节点仅访问一次，采用禁忌表tabuk来记录蚂蚁k当前走过的节点序号。当m只蚂蚁都完成了一次周游，回到出发节点，分别计算每只蚂蚁在本次周游中所走过的n条边的总长度，并记录下其中最短的长度和对应的节点顺序。同时，根据本次蚂蚁周游过程中经过的路径，更新n(n-1)/2条边上的信息素浓度。首先计算信息素随着时间的流逝挥发后n(n-1)/2条边上的信息素剩余量，

τij=(1-ρ)τij。

(2)

式中ρ表示信息素挥发系数，且0<ρ≤1。

其次考虑蚂蚁本次周游过程中在它们所经过的路径上释放的信息素：

(3)

(4)

蚂蚁遍历完所有节点，n(n-1)/2条边上信息素浓度完成更新，禁忌表清零，蚂蚁周游次数增加一，重新将m只蚂蚁随机放置在n个节点，准备下一次周游。

当蚂蚁周游次数达到预定最大周游次数时，停止循环，输出执行整个算法得到的最优路径及其长度[5]。

蚁群算法具有鲁棒性强、分布式计算、易于与其他算法结合的优点，但也有易收敛于局部最优解的不足[6]。为了加强蚁群算法的全局收敛性和加快收敛速度，多位研究者从不同角度对蚁群算法进行了改进：文献[7]提出了改进型量子蚁群算法，引入信息素挥发因子的自适应动态更新策略，并将传统的旋转门变换成Hδ；文献[8]将蚁群算法与粒子群算法相结合，综合了二者的优势；文献[9]将遗传算法与蚁群算法结合，由蚁群算法生成遗传算法的初始种群，再用改进遗传算法进行寻优。

2 本文改进算法

文献[10]提出一种改进2-opt和蚁群混合算法来求解TSP，提高了算法的寻优性能和收敛性，但是没有达到理论最优解，且进行了1 000次的迭代次数，算法运算时间过长，算法仍需进一步改进。本文沿用文献[10]的思路，先进行全局寻优，找到局部最优解，再利用局部搜索不断优化所求解，最终得到全局最优解。

2.1 结合贪心算法

贪心算法又被称作贪婪算法，是一种常见的寻优算法。贪心算法的核心思想是用局部最优解去逼近全局最优解，在寻优过程中总是做出当前情况下的最优选择，能够在较短时间内找到较为满意的解[11-12]。对于求解TSP，贪心算法的求解方法是每次选择未访问节点中的最近节点作为下一个节点，最终形成一条完整路径[13]。对比贪心算法和蚁群算法，发现蚁群算法其实是贪心算法的进阶算法：在全局搜索方面引入了信息素浓度这一贯穿时间和空间两个维度的变量，强化了算法的寻优性能；在下一节点选择方面引入了轮盘赌算法，以概率的方式选择下一个节点而不是一味地选择最优节点。

文献[14]对基本蚁群算法进行了改进，定义并引入了间接期望启发式(5)和间接期望启发式因子γ，并将节点转移概率计算公式改进为式(6)，加强了节点距离在整个节点转移概率计算中的影响力，避免了算法运算后期信息素浓度影响度过大造成算法陷入局部最优解。

(5)

(6)

其中：γ表示间接期望启发式因子，代表间接期望启发式对状态转移概率计算的影响度，即节点j与除节点i以外的其他节点之间距离的均值对状态转移概率计算的影响度。

本文采用文献[14]中类似的改进方案，对贪心算法进行改进，将贪心算法选择下一节点的计算方式规定为式(7)：

(7)

在蚁群算法寻优过程中，最需要解决的问题就是算法因局部最优解上的信息素浓度过高而无法找到全局最优解。在蚁群算法中，能够影响下一节点选择的只有信息素浓度和节点之间距离两个因素，信息素浓度的影响度决定着收敛性，节点之间的距离的影响度决定着多样性，二者处于一种微妙的平衡之中。信息素浓度是可以经过时间的积累不断增强的，这也是蚁群算法能够通过不断迭代进行寻优的精髓所在，而节点之间的距离则是固定不变的。通过对蚁群算法仿真计算的观察，算法大约经过100次迭代就能寻找到一个较优解，而此时大量的信息素不断积累，使得算法难以走出局部最优解。

为了加强算法路径的多样性，本文提出用改进贪心算法短期替代蚁群算法进行寻优的方案。当1≤NC<0.25×NCmax时，采用式(6)计算状态转移概率；当0.25×NCmax≤NC<0.5×NCmax时，采用式(7)计算状态转移概率；当0.5×NCmax≤NC≤NCmax时，采用式(6)计算状态转移概率。即当0.25×NCmax≤NC<0.5×NCmax时，仅考虑期望启发式ηij和间接期望启发式zij对转移概率计算的影响，不再考虑信息素浓度，但是这期间不影响信息素的积累与挥发，即改进后的贪心算法也引入了本次迭代最优路径上信息素浓度的积累机制和全部信息素浓度随时间变化的挥发机制，只是不影响下一节点的选择。

2.2 引入变异算子

变异算子是求解TSP中较为常见的一种局部搜索方法，借鉴遗传算法中的变异方法，本文采用逆转和插入两种变异算子代替文献[10]中的2-opt算法作为局部搜索算子。

所谓逆转算子，即将原路径中部分由连续若干个节点组成的片段进行翻转，设原路径为{4，0,1,3,5,8,9,7,6,2}，随机生成两个2到9之间不相等的数字2和6，则原路径中对应的节点为0和8，经过逆转变换后得到新路径{4,8,5,3,1,0,9,7,6,2}。

所谓插入算子，即将原路径中某个节点调动到另一个节点之后，其余节点顺序保持不变，设原路径为{4，0,1,3,5,8,9,7,6,2}，随机生成两个2到9之间不相等的数字2和6，则原路径中对应的节点为0和8，经过插入变换后得到新路径{4,0,8,1,3,5,9,7,6,2}。

在蚁群算法每次迭代完成之后，使用逆转、插入算子进行局部优化。采用遗传算法优胜劣汰的理念，若新生成的路径更优，则保留新路径舍弃原路径，否则保持不变，每次迭代分别用逆转、插入算子变换n次。

3 算法执行步骤

如图1所示，本文算法的执行步骤如下：

步骤1初始化各项参数，α，β，γ，η，τ，ρ，Q，m，n,NC,NCmax。

步骤2将m只蚂蚁随机放置在n个节点。

步骤3判断NC大小，选择对应的状态转移概率公式，m只蚂蚁按照式(6)或者式(7)选择下一节点，完成本次循环。

步骤4用逆转、插入算子优化蚁群算法所得解，记录优化后所得本次循环中最短的路径及其长度。

步骤5更新各条路径上的信息素。

步骤6判断NC是否小于等于NCmax，如果满足条件，则NC=NC+1，并跳转至步骤2；否则，停止循环，输出所有循环中最短的路径及其长度。

4 算法改进仿真比较

本文算法在MATLAB软件平台下对eil51、eil76和eil101数据模型进行20次仿真求解，得到的最优解路径如图2～图4所示。本文算法是在文献[10]的基础上进行的改进，文献[10]仅针对最优解求解结果进行了展示，文献[15]提出一种改进蚁群算法对eil51、eil76和eil101数据模型进行了求解，并对最优解结果和平均值结果都进行了展示。为验证本文算法的求解性能，将本文算法的求解结果与文献[10]中求得的最优解、文献[15]中求得的最优解和平均解以及TSPLIB提供的理论最优解进行比较，在参数设置上采用与文献[10]相同的设置，即α=1,β=3,γ=3,NCmax=500,ρ=0.5，Q=10∧6，m=n。

如表1和图5所示，相比于文献[10]中的算法，本文算法求得的最优解更优，相比于文献[15]中的算法，最优解和平均值都有所优化，寻优能力得到了进一步加强。具体来说，在eil51模型中，求得的最优解就是理论最优解，20次仿真结果的平均值与理论最优解也只有不到1的差距，而在节点规模较大的eil76和eil101模型中，求得的最优解也已十分接近理论最优解。而且在文献[10]文献[15]中，算法运行的最大迭代次数设置为1 000，而本文算法仅需将最大迭代次数设置为500即可得到满意的结果，大大缩短了算法寻优时间。

本文算法在求解eil76和eil101中求得的最优解与理论最优解还有一些差距，为了进一步提高算法求得的最优解，对本文算法原理进行分析，本文算法在节点规模更大的eil76和eil101数据模型中无法达到理论最优解，一方面是因为模型节点规模扩大，局部最优解数量增加，全局最优解的寻找难度增大，另一方面是因为本文算法在求解TSP问题时，依靠局部优化来实现从局部最优解向全局最优解的调整，而如果最初的局部最优解与全局最优解相差很大，局部优化的工作量会很大，通过局部调整无法达到全局最优解，下一步改进的方向可以减小最初得到的局部最优解与全局最优解之间差距，使其经过少量的局部调整就能够达到全局最优解，即提高全局搜索中得到的局部最优解的质量，为之后的局部调整打好基础。

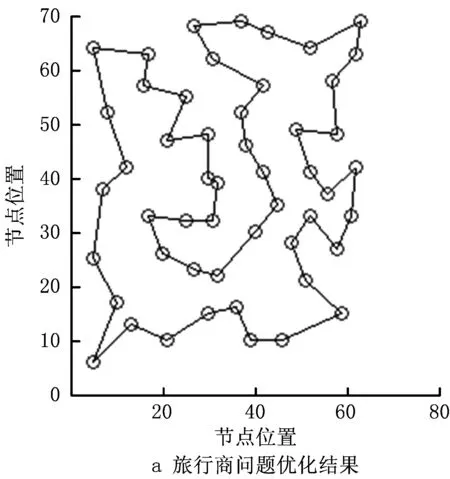
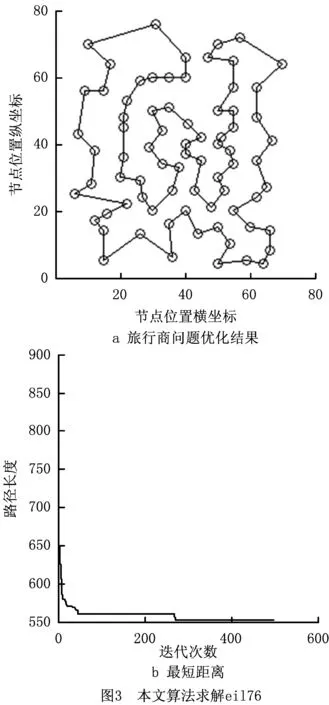
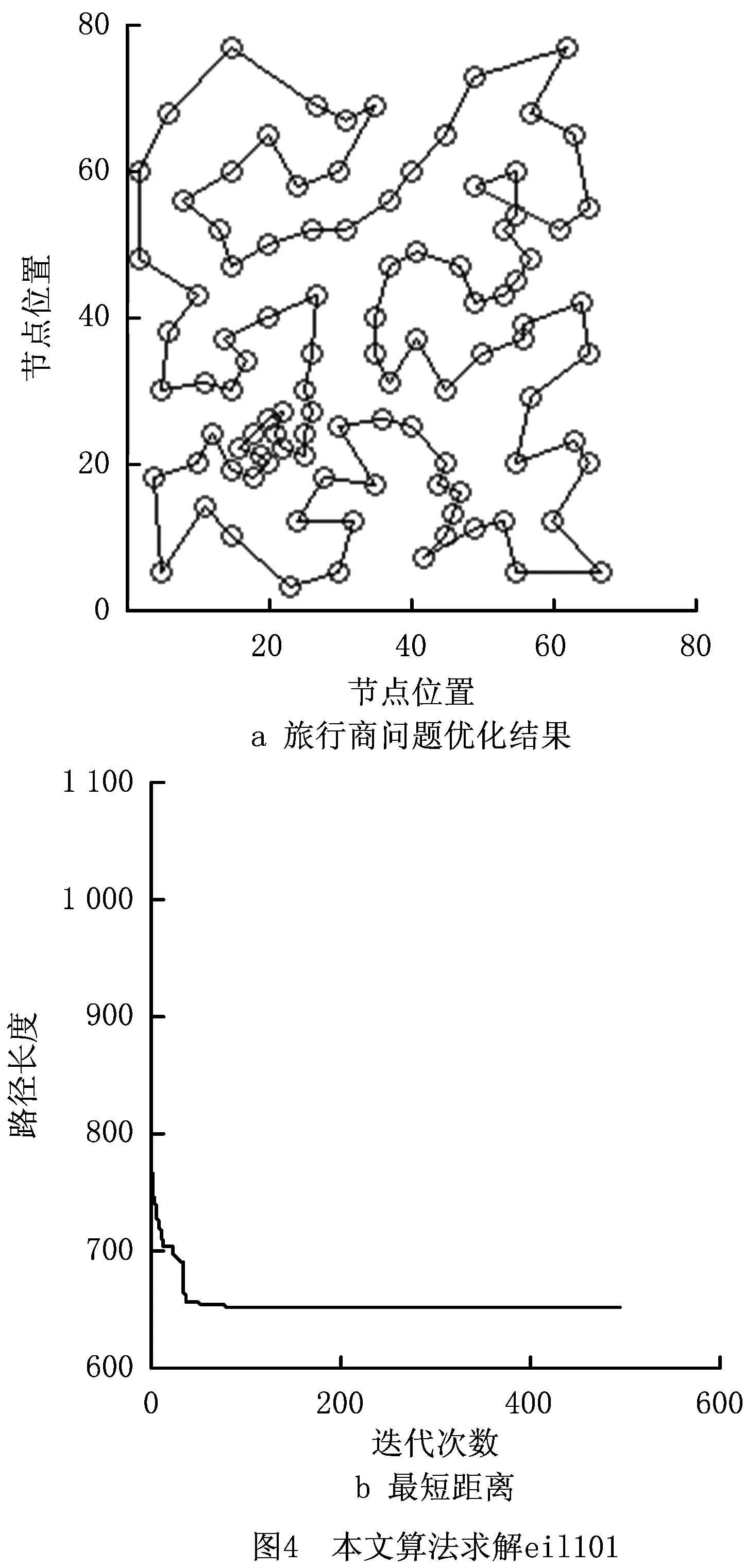
表1 算法改进仿真比较

5 参数优化仿真比较

5.1 参数优化方法介绍

在文献[10]中，算法的参数设置借鉴了文献[16]中的数值，将参数分别设置为α=1,β=3,γ=3。为了寻找更优的参数组合方案，文献[17]采用控制变量法，改变其中的一个参数，比较算法的寻优性能和收敛性能。这样的方法看似合理，但随着对算法设置研究的深入，发现蚁群算法的参数之间存在着互相制约的关系，不能简单地采用控制变量法来确定参数组合，那样会割裂参数之间的联系，无法找到最优的参数组合[18]。

文献[19]认为，可以将蚁群算法的参数设置问题看作一个新的组合优化问题，使用启发式算法来求解这个参数组合优化问题的最优解。本文采用差分进化算法求解参数组合优化问题。

差分进化算法类似于遗传算法，最大的不同点在于利用个体间的差异实现变异。首先计算随机选取的个体与另外两个个体之间的差值，再将差值进行缩放后与选取的个体相加，生成新的个体。差分进化算法的交叉和选择与遗传算法相同[20]。交叉过程是将种群中两个较优个体的片段从原先个体中断开，互相交换片段后生成新的两个新个体；选择过程则是典型的优胜劣汰机制，使用评价函数的计算结果作为评价标准，新生成的个体代入评价函数进行计算，结果比原先个体更优则保留，否则，舍弃。

与遗传算法不同，差分进化算法可以将种群内部的差异继承下来迭代给下一代，这样可以保持种群的多样性。而交叉过程又可以将多样性进行加强，产生更多不同的个体。

基本差分进化算法涉及到3个主要控制参数，分别是种群规模NP，变异算子F及交叉概率因子Cr[21]。文献[22-23]中指出，NP的取值为(5×D，10×D)(D代表问题的维数)，F的较好取值为0.5，Cr的取值为(0.4，1)。本文并非针对差分进化算法的研究，因此借鉴文献[22-23]中的结论取NP=30，F=0.5，Cr=0.4。

将蚁群算法的参数组合作为差分进化算法求解的三维组合优化问题，将蚁群算法的寻优结果作为差分进化算法的评价函数，为了减少嵌套算法的计算总时间，设最大迭代次数T=20。具体步骤如下(如图6)：

步骤1初始化各项参数，N,F,CR,T。

步骤2随机生成参数设置的初始种群。

步骤3参数设置种群进行变异、交叉。

步骤4将变异、交叉后所得的参数个体分别代入改进蚁群算法中作为参数进行迭代寻优，根据寻优结果进行差分进化算法的选择。

步骤5如果变异、交叉后生成的参数个体优于原先的参数个体，则用新生成的参数个体替换原先的参数个体；否则，舍弃新生成的参数个体。

步骤6判断迭代次数是否小于等于T，如果满足条件，则迭代次数增加一，并跳转至步骤3；否则，停止循环，输出最后一次迭代中最短的路径长度及其参数设置。

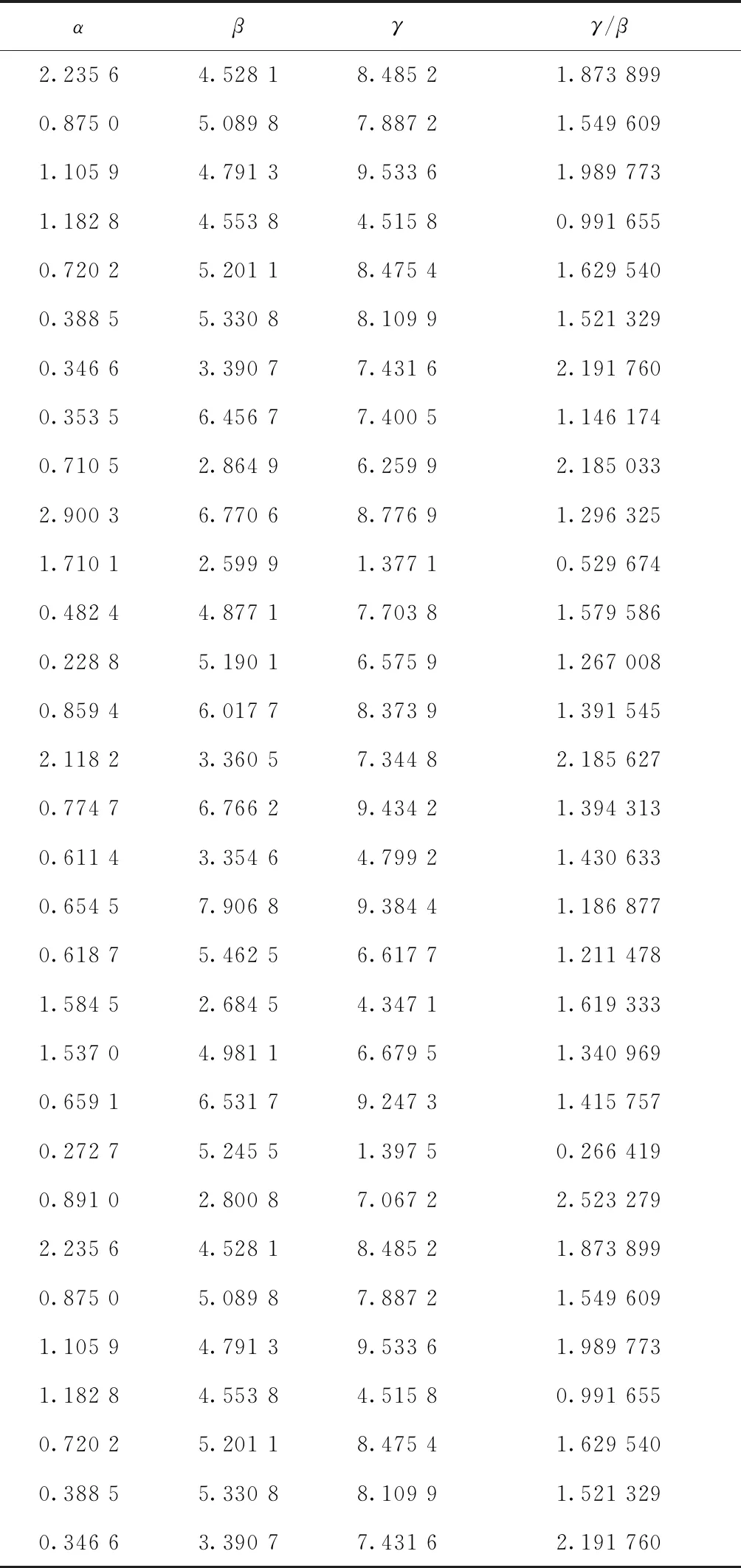
由于本文蚁群算法的最终求解结果不仅受参数影响，还受贪心算法和局部搜索算法的影响，为了最大程度地减少不相关因素对算法整体寻优性能的影响，本文使用差分进化算法嵌套文献[14]中的改进蚁群算法求解burma14数据模型，各个文献中算法之间的关系如图7所示，输出参数组合和对应的最优路径长度，将能够得到理论最优解30.878 5的参数组合进行记录，如表2所示。

表2 仿真结果

αβγγ/β2.235 64.528 18.485 21.873 8990.875 05.089 87.887 21.549 6091.105 94.791 39.533 61.989 7731.182 84.553 84.515 80.991 6550.720 25.201 18.475 41.629 5400.388 55.330 88.109 91.521 3290.346 63.390 77.431 62.191 7600.353 56.456 77.400 51.146 1740.710 52.864 96.259 92.185 0332.900 36.770 68.776 91.296 3251.710 12.599 91.377 10.529 6740.482 44.877 17.703 81.579 5860.228 85.190 16.575 91.267 0080.859 46.017 78.373 91.391 5452.118 23.360 57.344 82.185 6270.774 76.766 29.434 21.394 3130.611 43.354 64.799 21.430 6330.654 57.906 89.384 41.186 8770.618 75.462 56.617 71.211 4781.584 52.684 54.347 11.619 3331.537 04.981 16.679 51.340 9690.659 16.531 79.247 31.415 7570.272 75.245 51.397 50.266 4190.891 02.800 87.067 22.523 2792.235 64.528 18.485 21.873 8990.875 05.089 87.887 21.549 6091.105 94.791 39.533 61.989 7731.182 84.553 84.515 80.991 6550.720 25.201 18.475 41.629 5400.388 55.330 88.109 91.521 3290.346 63.390 77.431 62.191 760

5.2 各参数分布区间统计

由表3和图8可见参数α的分布区间主要是(0，1)，参数α位于区间(0，1)的比重超过了60%，少量分布于(1，2)，极少数大于2，而且大于2的部分也是处于(2，3)这个区间，并没有出现极大的数值。由表4和图9可见参数β的分布区间主要是(4，6)，少量分布于(2，4)和(6，7)，极少数大于7。由表5和图10可见参数γ的分布区间主要是(7，9)，少量分布于(4，7)和(9，10)，极少数小于4。

表3 参数α分布区间

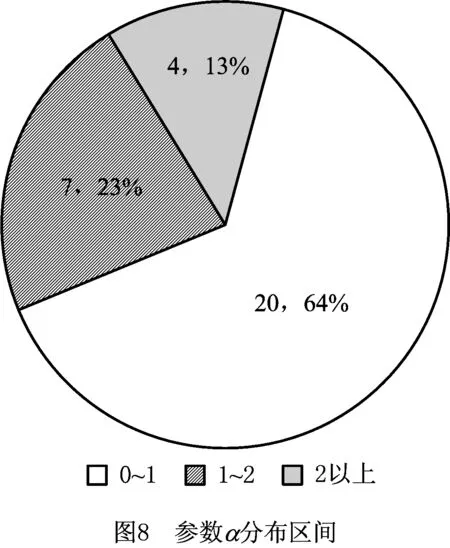
表4 参数β分布区间

分布区间β2～343～444～585～696～757以上1

表5 参数γ分布区间

分布区间γ4以下24～546～747～888～989～105

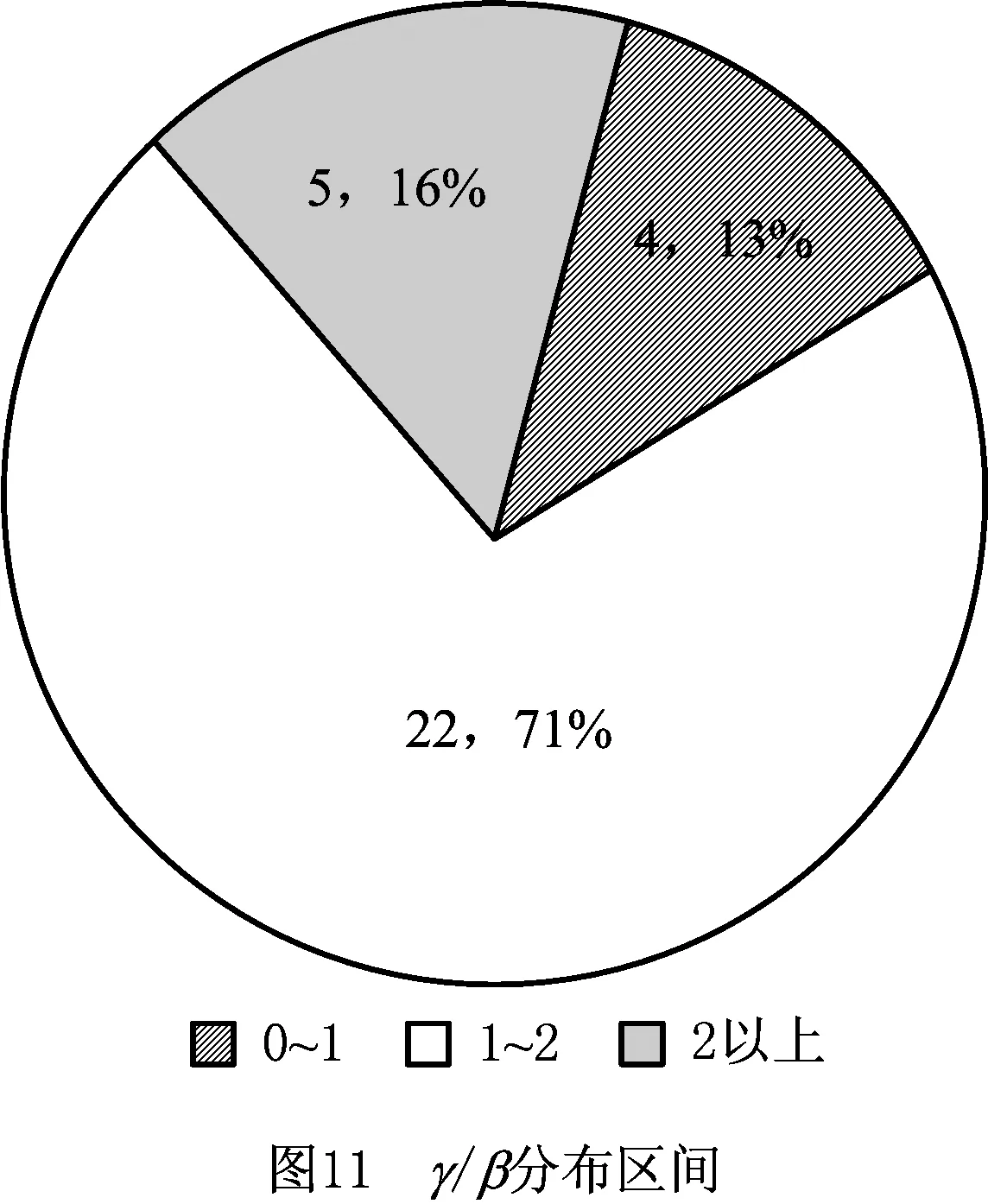
表6 γ/β分布区间

分布区间γ/β0～141～2222以上5

5.3 参数设置优化结果及验证

经过对3个参数分布区间以及β和γ的相互制约关系γ/β分布区间的简单分析，初步可以得到以下结论：

(1)参数α的理想取值是0.5。

(2)参数β和γ的取值既要考虑两者的分布区间，同时要考虑两者的制约关系，综合以上分析β和γ的理想取值分别为5和8。

为验证以上优化结果的正确性，将α=0.5，β=5，γ=8代入本文算法，与α=1，β=3，γ=3进行寻优性能的仿真比较。当参数设置为α=0.5，β=5，γ=8时，算法对对eil51、eil76和eil101数据模型进行20次仿真求解，得到的最优解路径如图12～图14所示。如表7和图15所示，将参数优化前后仿真结果进行比较，经过参数优化后的本文算法寻优性能更加强大，在eil51和eil76数据模型中求得的最优解就是理论最优解，平均值也有所提升，对于节点规模较大的eil101数据模型的求解已经将求得的最优解与理论最优解的误差降低到1%以下。

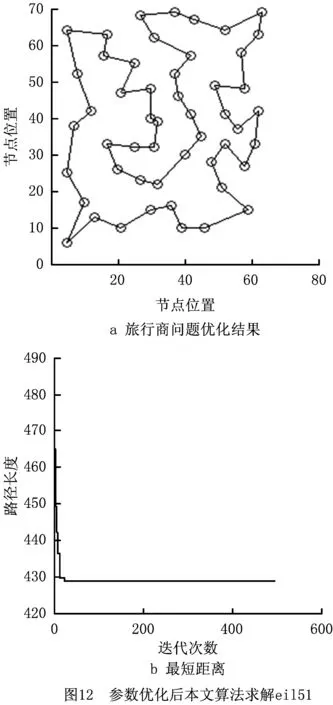
不可否认，经过参数优化的本文算法对于eil101数据模型还是无法求得理论最优解，说明在求解超过100个节点的TSP时，仅依靠参数优化无法让本文算法的求解性能满足eil101数据模型的求解需求，需要对整个算法的运行原理继续进行改进。

表7 参数优化仿真比较

6 结束语

本文在文献[10]的基础上进行了算法改进，为了平衡算法运行后期信息素浓度与节点距离对于状态转移概率计算的影响度大小，增强算法寻优的多样性，避免算法陷入局部最优解，引入了贪心算法，用变异算子替换了2-opt局部搜索算法，经过仿真求解TSP数据模型，验证了算法改进的有效性，强化了算法的寻优性能。此外，为了优化算法的参数组合，将算法参数视作一个新的组合优化问题，使用差分进化算法进行求解，得到了一组理想参数组合，并通过仿真求解TSP数据模型，验证了参数优化的有效性，进一步优化了算法，为参数设置提供了一种良好的解决方案。下一步的研究方向包括：①对算法的运行原理进行改进，使其能够满足100个节点以上的TSP数据模型的求解需求；②降低求得理论最优解的迭代次数，减少算法的运算时间。