聚散优化算法：一种新的启发式算法

李 瑞，赵新超,2+，郭 赛，袁健美

(1.北京邮电大学 理学院，北京 100876;2.湘潭大学 科学工程计算与数值仿真湖南省重点实验室，湘潭 湖南 411105;3.湘潭大学 数学与计算科学学院，湘潭 湖南 411105)

0 引言

启发式算法是通过对自然界生物种群的行为抽象和模拟构造而成的随机优化算法。这些算法的提出往往受到大自然的启发，例如Holland[1]通过模拟达尔文生物进化论的自然选择和遗传学机理的生物进化过程提出了遗传算法(Genetic Algorithm, GA)；Eberhart等[2]通过模拟鸟群在捕食过程中展现的智能行为提出了粒子群算法(Particle Swarm Optimization, PSO)；Dorigo等[3]通过模拟蚁群中蚂蚁相互之间通过信息素协作觅食的行为提出了蚁群优化算法(Ant Colony Optimization, ACO)；Storn等[4]在遗传算法进化思想的基础上提出一类基于群体的自适应全局优化的差分进化算法(Differential Evolution, DE)，是通过对进化机制和个体之间的差异信息的模拟提出的；Karaboga等[5]通过模拟蜜蜂的社会分工与协作觅食的行为提出了人工蜂群(Artificial Bee Colony, ABC)算法；Passino[6]模仿人体食道内大肠杆菌的觅食行为，提出了细菌觅食优化(Bactering Foraging Optimization, BFO)算法；头脑风暴优化算法[7]于2011年提出，算法模拟了一种人类集思广益求解问题的集体行为，即头脑风暴过程。自然界中的生物特别是蚂蚁、细菌等，它们每个个体都不具有类似于人类复杂的高级智能，但它们在食物的刺激下，不断适应环境，展现出了极高的群体智能，并且群体展现出的这种能力具有自组织的特点。这种现象为人类解决问题提供了新的角度。受此启发，本文认为可以将传统方法进行种群化改造，将原有的算子扩展为适合种群的算子，从而提出新的算法。目前已有许多专家学者提出了不同的启发式算法，并在实际生产生活中取得了不错的效果。例如，李军军等[8]提出的诱导蚁群粒子群算法有效解决了多自动导引车路径规划中的冲突问题；刘江伟等[9]基于改进粒子群算法解决了多工位装配序列规划问题。

本文探究是否可以将局部的传统优化方法进行种群化，从而使新设计的群体优化算法具有更好的全局搜索能力。传统方法多为单点搜索，相比于基于种群的算法，单点搜索更容易陷入局部最优，因而传统方法一般不具备全局搜索能力。另一方面传统方法对于一个局部问题的求解往往更加有效，将传统方法种群化之后，希望在增加传统方法全局搜索能力的同时，能够保持传统方法的搜索性能，从而开发出新的方法。基于该想法，本文在启发式算法和直接方法的研究基础上，将单纯形方法算子种群化，抽象出了聚合算子和分散算子。这两个算子在每次迭代产生新的种群，在该过程中利用启发式信息产生新的解。此外，本文还提出了归档重置的策略，该策略可以在一个较为宏观的尺度上对种群的演变进行引导。结合两个算子和归档重置策略，提出一种新的启发式算法并通过大量仿真实验验证了算法的有效性。数值实验表明在很多的测试函数上，该算法能够展现出较以往的启发式算法更优的性能。

1 单纯形法

单纯形法是可以不使用导数信息的一种传统优化方法，该方法是利用比较简单几何图形各顶点的目标函数值，在连续改变几何图形的过程中，逐步以目标函数值较小的顶点取代目标函数值最大的顶点，从而求优点的方法。单纯形是代数拓扑中最基本的概念，是三角形和四面体的一种泛化。k维单纯形是指包含k+1个节点的凸多面体。考虑实数域的n维向量空间Rn，设a0,a1,…,a_n是一组向量，使得a0-a1,a1-a2,…,an-1-an线性无关。设E={p=s0a0，s1a1，…,snan|s0+s1+…+sn=1}，点集E称为一个n维单纯形。例如：特殊的1维单纯形就是线段，2维单纯形就是三角形。

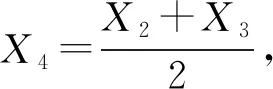
X5=X4+α(X4-X1)=-αX1+(1+α)X4。

(1)

则称为X5为X1关于X4的反射点，α为反射系数，一般取α=1。如图1所示。

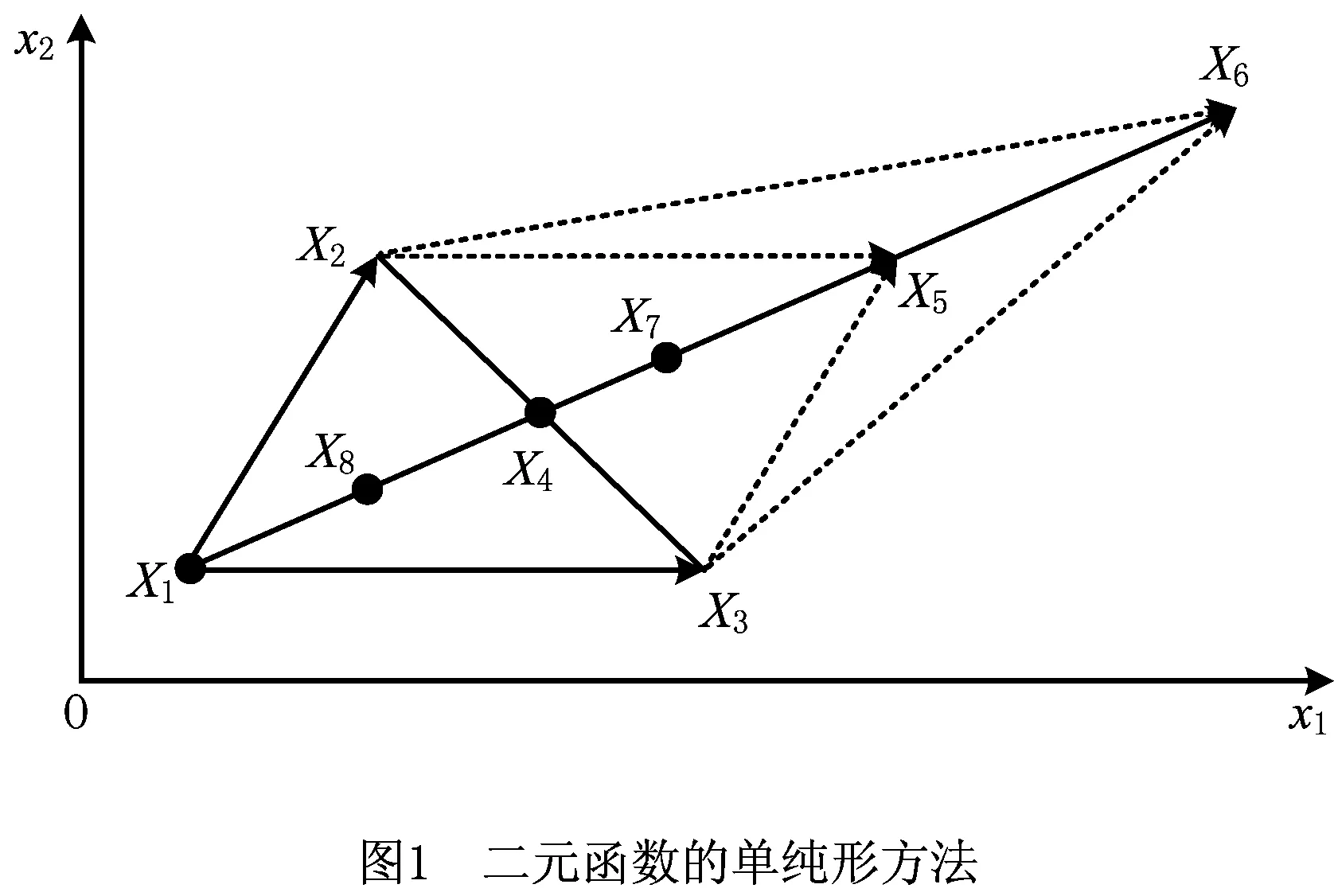
由此可以算出X5的函数值f(X5)可能有下列情形：

(1)f(X5)≤f(X3) 搜索方向正确，可进一步扩张，继续沿X1X5向前搜索(扩张)。其中α为扩张因子，可取值为1.5。若f(X6)≤f(X5)，则扩张有利，就以X6代替X1构成新单纯形{X2,X3,X6}；若f(X6)≥f(X5)，则扩张不利，舍去X6，以X5代替X1构成新单纯形{X2,X3,X5}。

(2)f(X3)≤f(X5)≤f(X2) 这说明搜索方向正确，无须扩张，以X5代替X1构成新的单纯形{X2,X3,X5}。

(3)f(X2)≤f(X5)≤f(X1) 这表示X5走得太远，应缩回一些。若以α表示压缩因子，常取α值为0.5，以X7代替X1构成新的单纯形{X2,X3,X7}。

(4)f(X5)>f(X1)X2与X1向X3收缩。

2 聚集算子和分散算子

受传统最优化方法中直接方法——单纯形方法的启发，本文提出了聚集算子和分散算子作为种群中新个体的生成策略，这样产生新的种群面临的最大的问题是如何使用原有携带群体信息和个体搜索信息的解来产生新的更优的解。借鉴单纯形方法，在生成每一个新解的时候都在种群中依次选取3个个体，并按照各自的目标函数值确定三者之中的最优者Xb，最差者Xw和中间者Xm，最后根据对3个解不同关系的讨论提出了聚集算子和分散算子。

2.1 聚集算子

聚集算子的目的是使种群在迭代的过程中向某一个有潜力的方向聚集。使用该算子在前期可以获得较快的收敛速度，后期具有向内聚集趋势的局部搜索能力。给定3个解，依据目标函数选出Xb,Xw,Xm，则让三者中最差的解向两个更优解的方向靠拢，为了加快算法的收敛速度，本文使用两个比较优秀的解来引导整个种群的更新。

在传统单纯形方法中，为了使新解向较优解靠拢，参数α的值应该大于0，另一方面为确保算法拥有较高的收敛性，通常最高的取值不应该超过2，因此参数α∈(0,2)。综合考虑式(1)，-α可以认为是对较差解x1的罚因子，α是对较好解x4给定的鼓励因子。现在仔细讨论一下不同情况时的算法表现，在α∈(0,1)时，由于参数小于1，说明算法没有搜索到较好的解，因此应当适度减弱原有策略的影响，故应将因子减小希望能够找到一个较好的解，此时对较差的解应该减弱处罚力度，同时减弱对较好解的鼓励力度；当α∈(1,2)时，说明原来的机制比较好，应当强化这个策略，增大因子的值可以增强对差解的处罚力度，增强对好解的鼓励力度。但是这个时候差解的权重为负，当处于算法后期3个解相差不大的情况下，需要很多奖励才能弥补这个过重的惩罚，对搜索不利，因此应当适度地进一步加大鼓励或者适度降低惩罚，从而进一步增强算法的效果。注意到将X1的系数改为1-α时更符合算法机制。此时，α∈(0,2),(1-α)∈(-1,1)而不是-α∈(-2,0)，即此时对较差解的惩罚相较于原公式大大减弱，符合上述判断。对式(1)分析易知，由于(X4-X1)的系数大于0，因此算法在产生新的探测点时很难取到三角形△X1X2X3的内部点，例如X8处的点。因此将式(1)中的1用α代替，从而弱化式(1)，使其能够包含三角形△X1X2X3内的点，得

(2)

进而引入随机数r1∈[0,2]，r2∈[0,1]构成凸组合得

X5=(1-r1)X1+r1(r2X2+(1-r2)X3)。

(3)

将算法中的个体带入上述公式，得到聚集算子的迭代公式，其中lBS是个体自身搜索到的最优解，gBS是算法到目前为止找到的全局最优解，随机数r1∈[0,2]，r2∈[0,1]，其中参数r1的选取范围是基于想扩大现有几个解组合的搜索范围，即属于扩展凸组合的参数选取方式。

Xi=(1-r1)Xi+r1(r2lBS+(1-r2)gBS)。

(4)

下面首先在二维空间内给出凸组合和扩展凸组合的结果，然后对式(4)给出一个直观的说明。

(1)凸组合 如图2所示，假设有3个二维平面向量OA，OB，OC，起点均在原点O。并且向量OA，OB不相等，随机数r∈[0,1]。则依据式(5)计算出OC的终点均落在向量OA，OB终点的连接线段AB上。

OC=rOA+(1-r)OB。

(5)

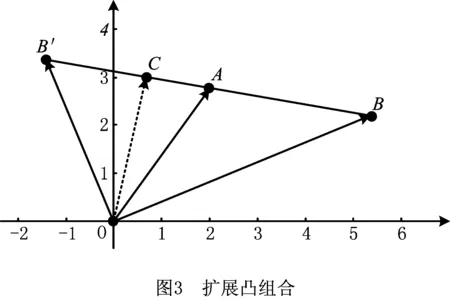
(2)拓展的凸组合 若式(5)中的随机数r∈[0，2]，如图3所示，向量OC的终点均落在线段B′B上，且|B′B|=2|AB|，即在A的另一侧作了和线段AB等长且共线的线段AB′。此时是在B′B直线上以A为中心，|AB|为半径的区间内进行搜索。简单证明如下：由式(5)可知A、B、C三点共线，且AC=(1-r)AB，故|AC|=|(1-r)AB|，又由于r∈[0,2]，故|AC|∈[-|AB|,|AB|]，因此C点位于A点两侧的线段B′B上，本文将这中操作称为拓展的凸组合。

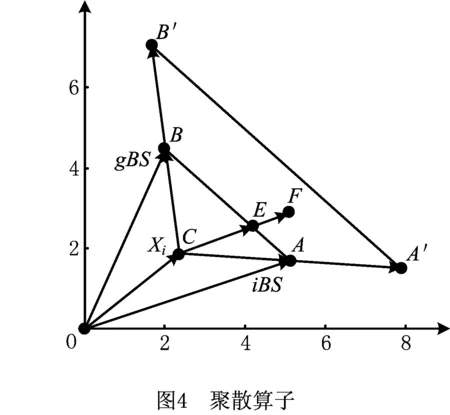
下图在二维空间内对式(4)给出一个直观的分析与阐释。如图4所示，已知向量OA，OB，OC分别代表lBS，gBS，Xi。首先由向量OA和OB得到一个向量OE，由凸组合情形分析知OE=r2×lBS+(1-r2)gBS的终点落在线段AB上，再由扩展的凸组合情形分析知，最终得到的向量OF会落到三角形区域A′B′C′内。当推广到n维欧式空间时，OF的终点会落到某一平面的某一个三角形区域内，从图形来看这个三角形区域是以AB为中位线，并且线段AB是由局部最优解和全局最优解连接而成，因此线段AB周围的区域非常有可能是一个有潜力的搜索区域。种群的每一个解及其个体最优解和当前全局最优解都会生成各自的三角形区域，在n维欧式空间，这些点会落到多个相交平面的三角区域内，这些平面相汇于A点。新的种群相较于上一代种群，整体上会以较大的概率向A点靠拢，因此叫做聚集算子。

首先根据式(4)，由每一个解的局部最优解和全局最优解生成一个新解，然后在这个解的周围区域进行搜索。在算法的前期，由于该个体最优解和群体发现的当前全局最优解的距离往往较大，两个解合成的临吋解和这两个解的距离比较远，该算子有较强的全局搜索能力。随着算法的进行，该算子以较大概率将群体中的解拉到算法群体发现的当前最优解附近，展现出对种群较强的引导作用。在算法的后期，全局最优解和个体最优解的距离一般较小，同时和种群内其他的解的距离一般也很小，此阶段该算子会在一个较小的区域内进行局部搜索，因此这时该算子又展现出算法所需要的局部搜索的能力。

2.2 分散算子

引入分散算子旨在算法搜索的后期种群内个体相似性较大的情况下，进行扩散以免种群陷入局部最优，同吋分散算子能够提供具有外向趋势的局部搜索能力。因为如果只是强调种群不断聚集，而一旦种群陷入局部最优解,如果没有外部驱动力就很难跳出来，所以本文提出的分散算子能够有一定的能力使种群始终保持一定的概率分散开，即有一定的概率朝着远离当前最优解的方向散开。具体迭代公式如下：

Xi=(1-2×r3)×Xb+r3×

(r4×Xw+(1-r4)×Xm)。

(6)

首先对下述公式进行简要的分析，其中随机数r3，r4∈[0,1]。

OD=(1-2×r3)×OC+r3×

(r4×OA+(1-r4)×OB)。

(7)

如图5所示，由式(7)得到的向量OD的中点落在线段CE′上。

OD=(1-2r3)×OC+r3(r4OA+(1-r4)×OB)

=OC+r3(r4×OA+(1-r4)×OB-2r3OC)。

(8)

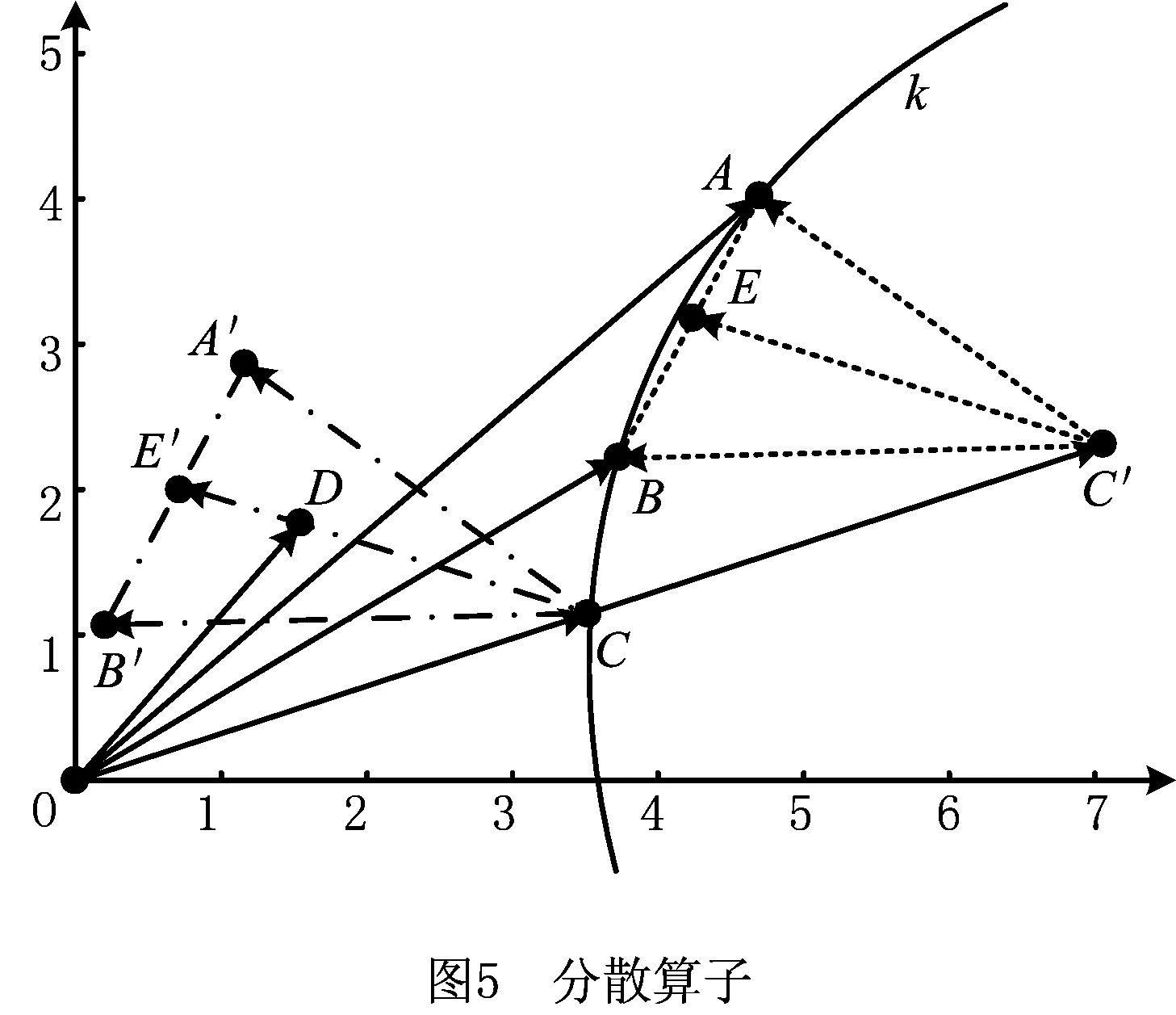
首先令OE=r4×OA+(1-r4)×OB，则由凸组合的性质知，点E落在线段AB上。令OC′=2OC，则C′E=r4×OA+(1-r4)OB-2r3OC，则OD=OC+r3×C′E。

当r3∈[0,1]时，向量OD的终端会落在图5所示的三角形△CA′B′区域中。由图5不难发现，沿着CO的方向便可以将三角形△C′AB平移到三角形△CA′B′的位置。

由于本文中只有当3个解的适应度值接近的时候才会启动分散算子，即当3个解大体处于同一个等高线k上时，才会用到分散算子。这时，分散算子能够以一定概率使新生成的解分布在父代等高线k的两侧。在算法后期该操作能够使算法得到的新解有一定的几率从原来的等高线分散开，从而保证算法在后期能够获得一定的跳出局部最优解的能力。若点A是已发现的全局最优点，如迭代公式(6)能够保证该算法搜索是在点A周围一定的范围内进行的。若目标函数是多峰函数，则极有可能由一个局部极小点跳跃到另外一个更有潜力的局部极小点。

3 允许重复的存档和种群重置策略

在启发式算法中都需要记录必要的历史信息，例如粒子群算法[2]必需要记录粒子的当前位置、速度和历史最优位置；蚁群算法[3]必需要记录各条边上的信息素浓度，这些信息主要是每个个体的局部信息。在一些算法中，经常使用存档的方式用于存储优秀的个体，再使用存档影响整个种群的迭代进程，特别是一些改进的算法中，使用存档记录特定的种群个体的方法能够使算法充分利用优秀个体的信息，从而提高算法的整体性能。例如文化算法使用了知识库来记录知识，这种知识库也是一种记录优秀个体的存档。

更新存档的方法也有许多，一般的做法是在保证多样性的前提下使用较好的个体替代存档中的个体，而且一般要求存档中个体彼此质检的差异比较大，以保证存档个体的多样性，从而使种群在存档信息引导的迭代过程中不至于过早地收敛。但是本文釆用的存档策略并不考虑多样性的问题，允许存档个体重复，故称之为允许重复的存档策略。该策略的思路是在种群迭代的过程中把比较优秀的个体保存到存档中，在种群更新很慢甚至是几乎停滞不前的时候，使用存档来重置种群。釆用这种测量的目的是充分利用种群迭代过程中的信息，以期获得较快的算法收敛速度。该策略包含允许重复的存档操作和种群重置操作两个操作，下面对这两个操作进行详细叙述。

3.1 存档操作

存档操作即将种群迭代过程中的信息保存到一个存档之中，在更新存档的时候并不要求存档中的个体各不相同。操作方式如下：

(1)首先设置一个存档，使存档的规模和种群规模一致，这样做只是便于直接将存档赋值给当前种群的重置种群操作。

(2)在更新存档时，依次选择一个当前存档中的空白个体或者年龄最大的个体作为被更新的个体，在每次迭代过程中需要比较当代种群的最优个体是否优于被更新的个体，如果优于被更新的个体则使用当代种群的最优个体替换被更新的个体，否则不更新。根据以上操作可知，使用这种方式产生的存档中会出现相同的个体，尤其在算法的后期所有的个体都差别不大，因此这是一种允许重复的存档操作。这种操作仍然有效的原因是：在算法的前期存档内的个体变动比较大，存档的重置起到了类似于轮盘赌在遗传算法[1]中的作用，即越是优秀的个体在存档中所占的比率越大，因此契合于适者生存的进化法则。这种做法使算法收敛速度加快，但也增加了陷入局部最优解的可能。

3.2 种群重置操作

根据允许重复的存档操作的特性，单纯使用存档直接更新种群会增加算法陷入局部最优解的可能，因此，对种群重置操作需要增加一些调整以降低这种风险。本文的思路是在重置种群时从多种重置方式中选择一种重置种群。因此对这种重置策略，重置种群操作中重置时机和重置方式的选择至关重要。

3.2.1 两种重置时机

重置时机的选择需要根据种群中最优解的变动情况决定。例如先前10代以内的种群都未曾产生更优秀的解，则一般可以认为种群的搜索已经陷入了局部陷阱。将种群规模的影响考虑进去，就得到本文所采取的判定方式：PopuSize代以内的种群产生优解的次数少于PopuSize/10，则重置种群。但这种触发机制并不全面，首先这种触发方式很难避免在PopuSize代以内的无用操作；其次更新代和更新次数作为参数需要人为调节。基于此，本文又提出另外一种随机更新方式，即设置一个很小的概率用于判断是否重置种群。这样可以以一定的概率提前结束掉无用的操作，但是该种群重置策略的概率阈值比较难确定，本文采用的概率是1/PopuSize。

3.2.2 三种重置方式

本文根据使用存档信息的多少将重置种群策略分为直接利用存档重置，间接利用存档重置和不利用存档重置。依据3种不同的思路，本文提出3种存档的更新方式。

(9)

([UB]j-[LB]j)。

(10)

(3)不使用存档重置 这种方式不使用存档和当前群体的历史信息，完全随机的重置种群。这种方式虽然可以增加种群多样性，避免算法陷入局部最优，但是由于这种方式完全不使用存档的信息，因此种群搜索模式变坏的可能性极大，则该操作发生的概率要足够的小，否则算法会丢失已获得的有效信息，从而丧失局部搜索能力。

综合考虑上述两种重置时机和3种重置方式之后，本文采取一种混合式的重置方式。首先，当PopuSize代以内的种群产生更优解的次数不超过PopuSize/10时，采用归档直接重置的方式(即方式1)重置；然后，当PopuSize代以内的种群产生更优解的次数不少于PopuSize/10时，产生一个随机数r∈[0,1]，若r<1/PopuSize，则采取3种重置方式的混合形式进行重置，否则，不重置。对于3种重置方式的混合策略，本文设置3种方式的使用概率分别为0.5、0.25、0.25。虽然这种重置方式看似比较复杂,但是其中的逻辑可以完全自洽，相互之间可以形成比较有效的合力。具体的伪代码如下。

算法1重置操作。

输入:连续每代均生成较优解的次数t。

1：if种群产生更优解的次数t≤PopuSize/10

2：直接使用存档重置种群；

3：else if r1<1/PopuSize then

4: if r2<0.5 then

5： 直接使用存档重置种群；

6： else if r2<0.75 then

7： 间接使用存档重置种群；

8： else

9： 随机重置种群；

10： end if

11：end if

12：将当前存档中的空白个体或者年龄最大的个体确定为目标个体；

13：if当代种群的最优个体是否优于目标个体then

14： 使用最优个体替换目标个体；

15：end if

3.3 聚散算法

结合聚集算子、分散算子和存档重置策略，本文提出了聚散算法。算法流程如下：第一步初始化种群，

(11)

算法2聚散算法。

1： stepl:初始化种群，并计算目标函数值；

2： step2:更新存档；

3： step3:判断是否需要重置种群；

4： step4:使用聚散算子生成新的个体并计算目标函数值；

5： step5:根据目标函数值更新种群；

6： step6:判断是否结束算法，如果不满足结束条件就返回到step2.

4 算法对比仿真实验

为验证算法的有效性，本文选取CEC测试库的20个测试函数，4个经典群智能算法：标准粒子群优化算法[10](Standard Particle Swarm Optimisation, SPSO2011)，带复合实验向量生成策略和控制参数的差分进化算法[11](Differential Evolution with Composite trial vector generation strategies and control parameters, CoDE)，策略适应性的差分进化算法[12](Differential Evolution algorithm with Strategy adaptation, SaDE)，智能全局的和声搜索算法[13](an Intelligent Global Harmony search, IGHS)，并对其进行了大量的仿真模拟实验。这4种优化算法属于3种不同的优化框架和搜索机理，能够反映选择的比较算法对象的多样性，其中SPSO是一个十分经典的粒子群算法，CoDE和SaDE是经典的差分进化算法变种，IGHS是一个优秀的和声搜索算法变种，这些算法的收敛速度快、搜索效率高，是常用的基准算法。本文实验平台是：CPU：Intel i7-3770，3.4 GH，内存：4 G，软件：MATLAB 2015b。

4.1 测试函数

本文在CEC2005[14]和CEC2014[15]测试函数集中选取了20个测试函数。具体函数名称或表达式如表1所示，其中fi(x*)是理论计算的函数最优值，每一维的搜索空间均为[-100，100]30，f1～f7是单峰函数，其余均为多峰函数。

表1 测试函数

续表1

4.2 实验仿真结果对比与分析

为验证算法的有效性，每个算法均独立运行30次，种群规模均设置为10，最大函数计算次数为60 000，算法所需的其余参数均遵循相关参考文献的建议。图6给出5种算法在求解优化问题过程在每一次迭代中的最优函数值随着迭代变量的变化曲线，该在线最优函数值的对比能够反映每一个算法在整体搜索过程中的动态变化趋势。表2给出5种算法求解函数优化问题获得的最终的最优结果，该结果能够反映算法的整体优化性能。

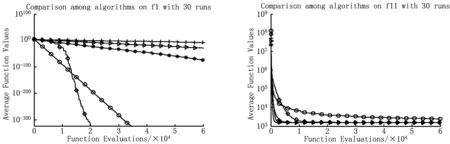
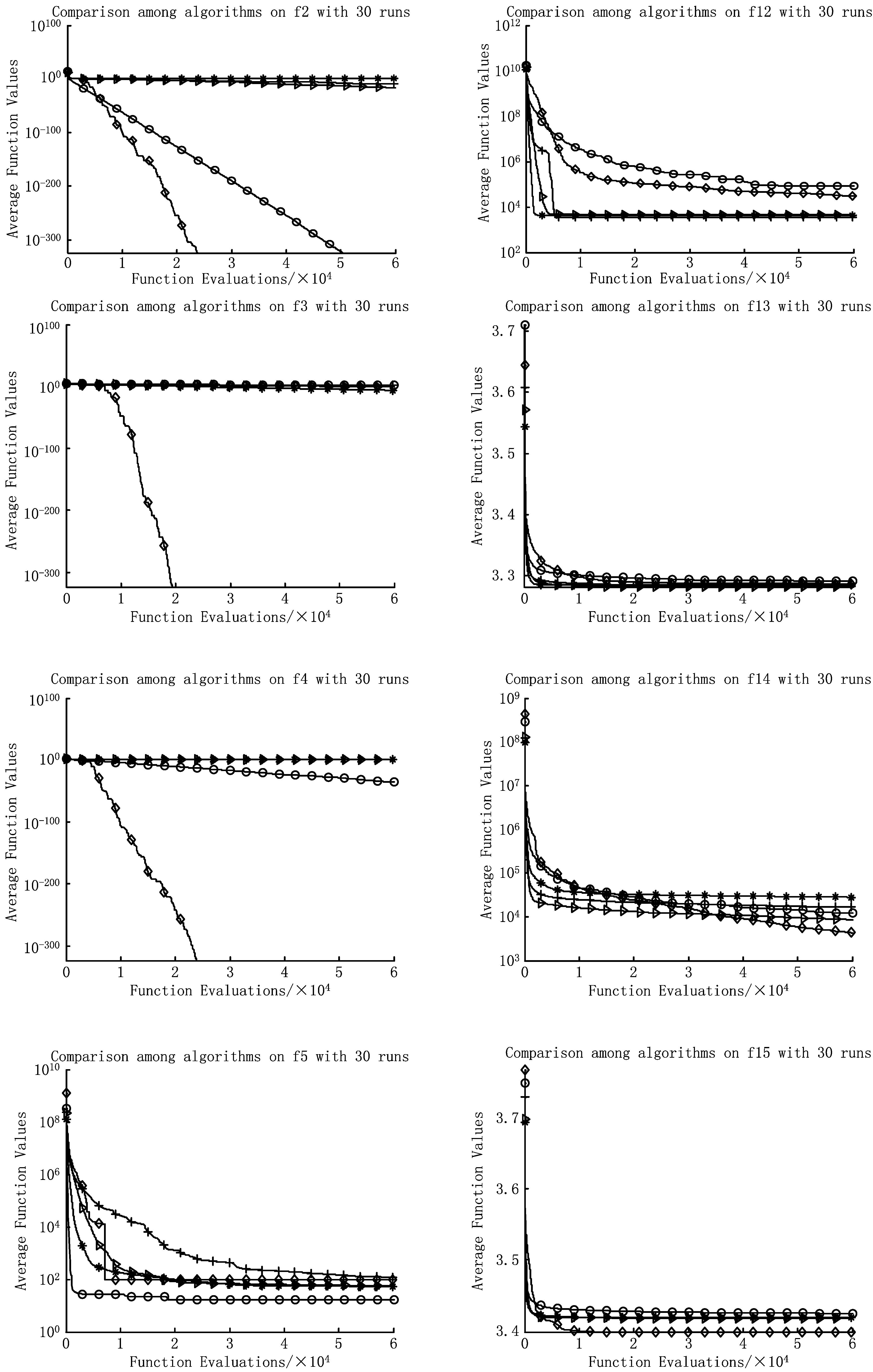
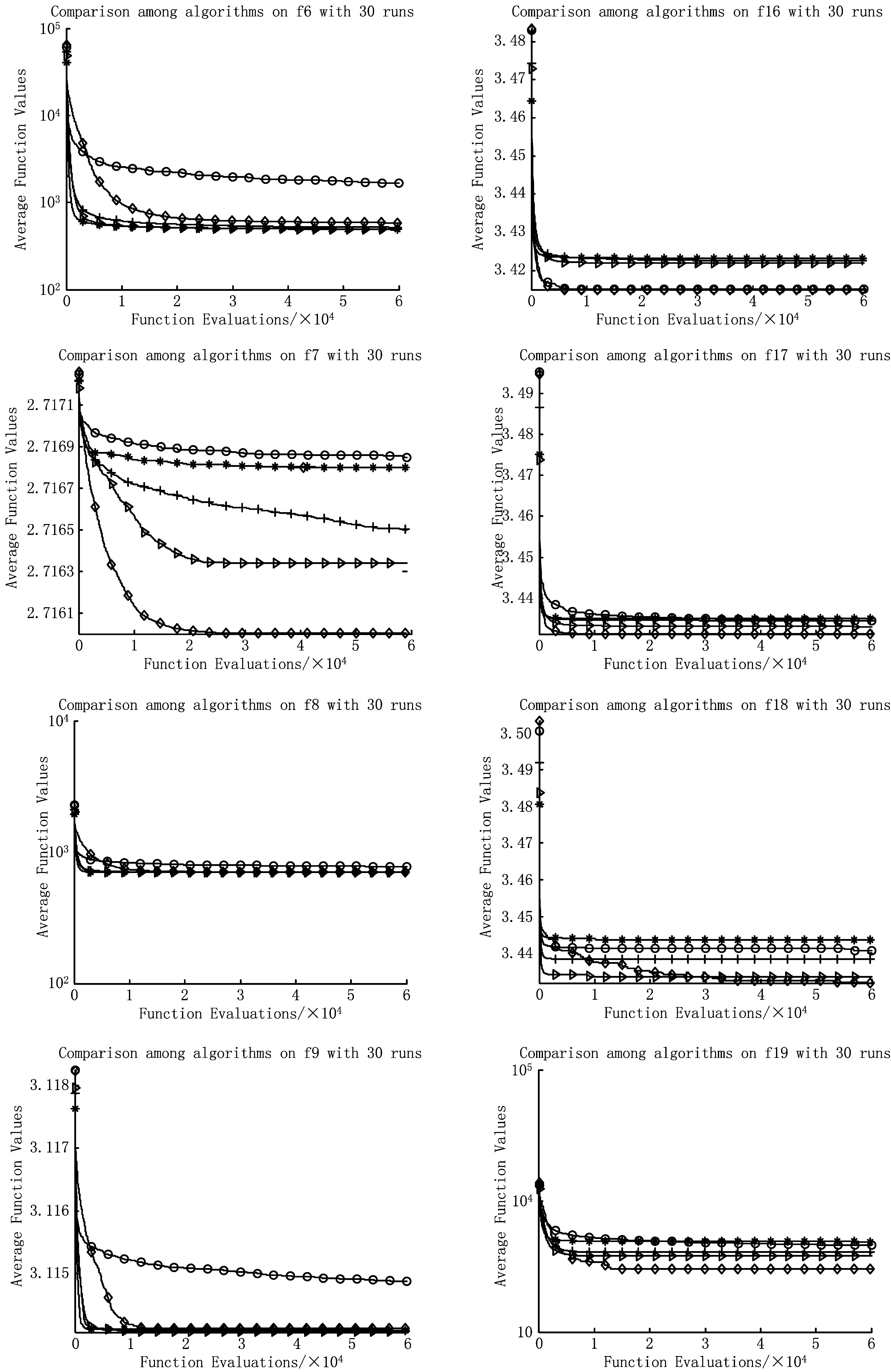
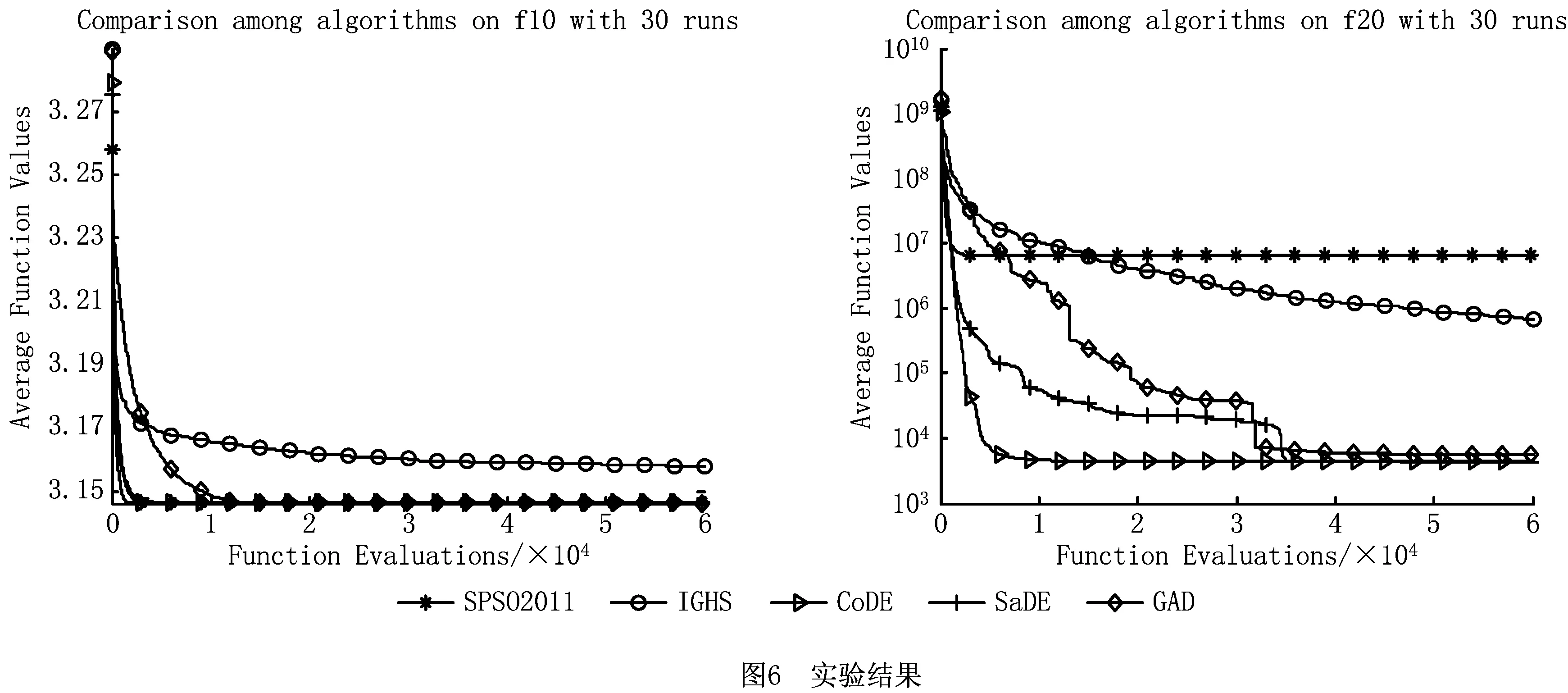
从不同算法收敛曲线对比图6可以直观看出本文提出的聚散算法GAD的整体性能较为优异，具有较优的探索功能和收敛性能，在大多数测试函数中能够取得和其他算法相近或更优秀的解，从而说明本文提出的聚散算子以及相应算法的有效性。

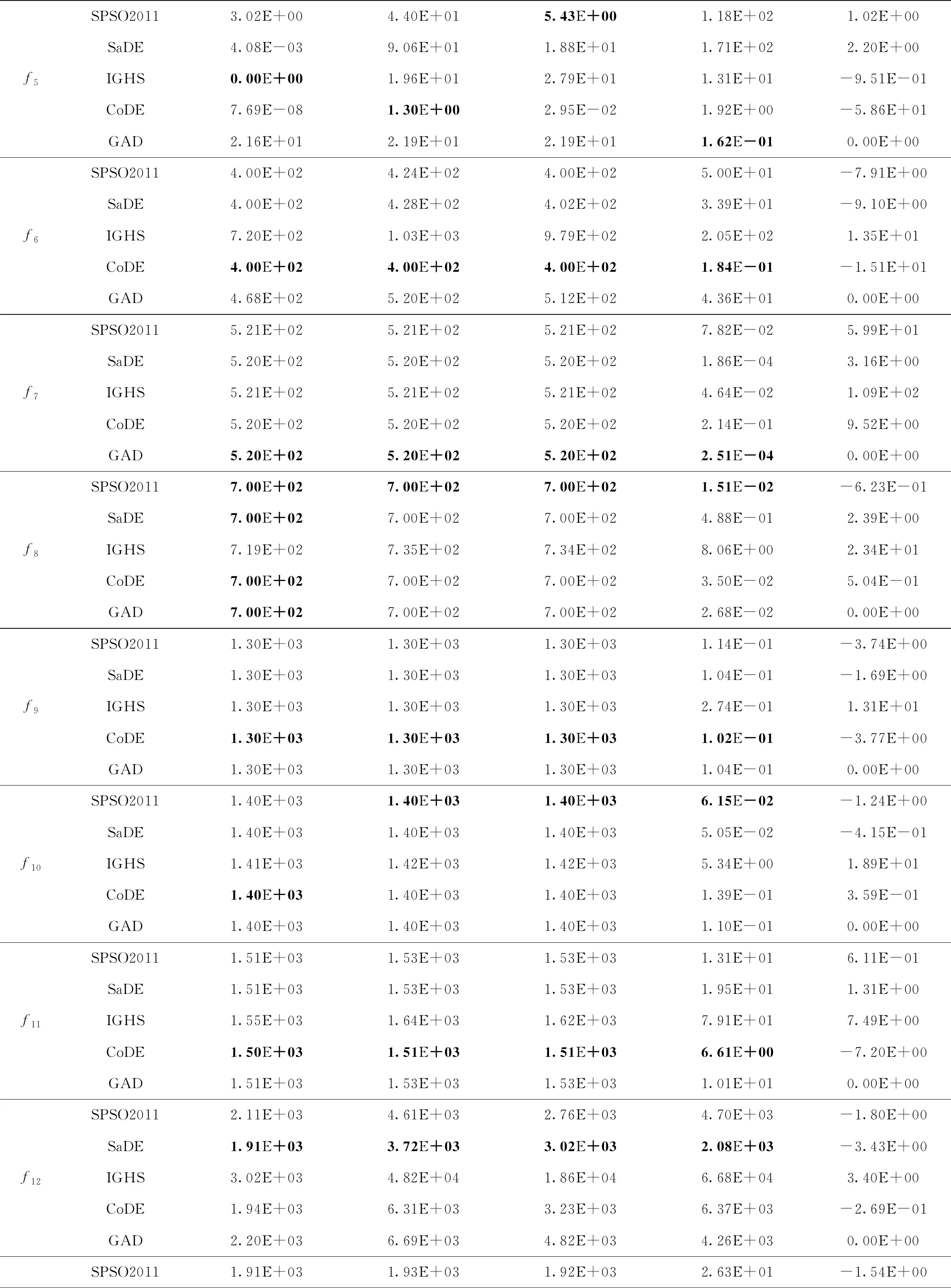
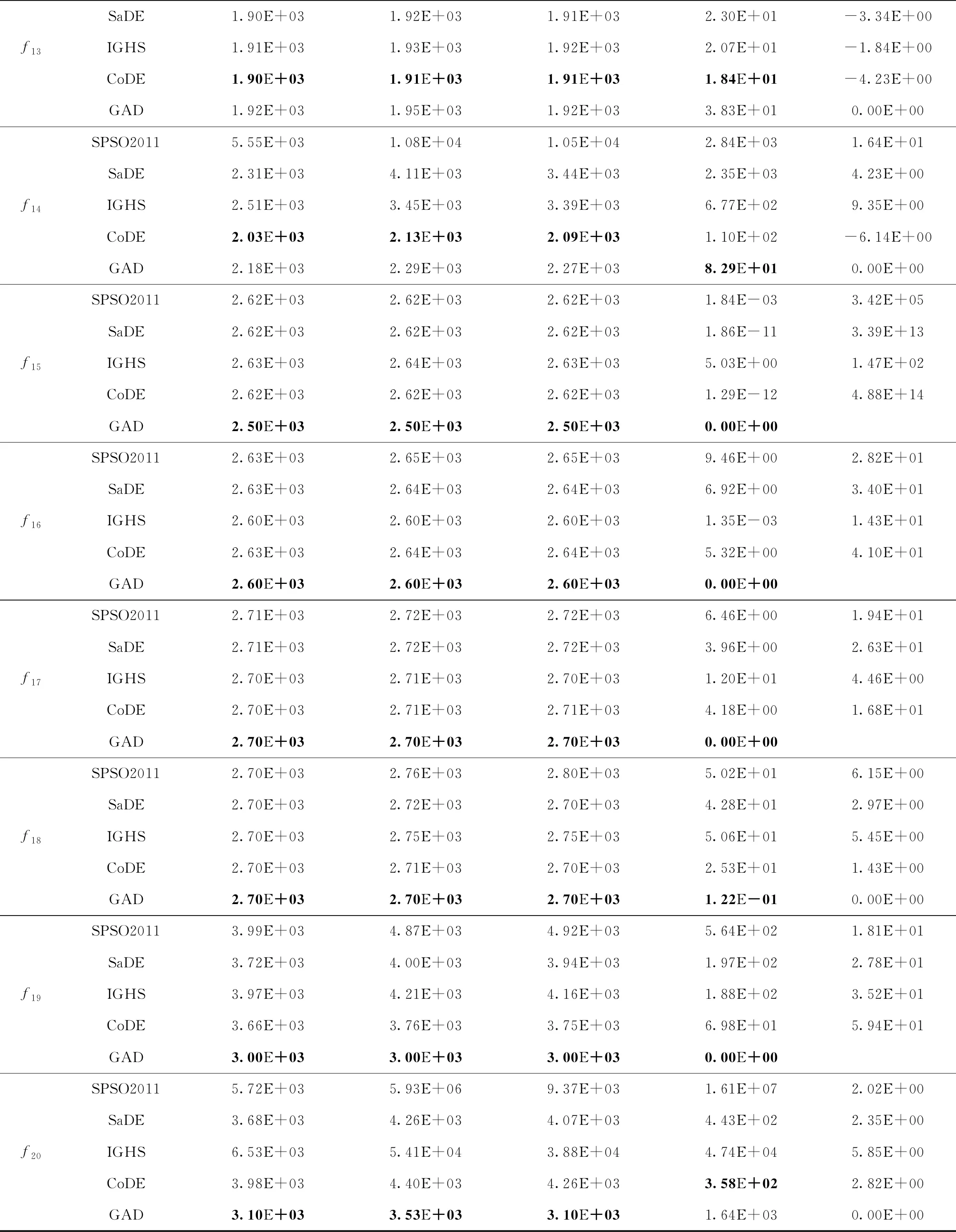
数值实验的最终结果如表2所示，通过对具体实验数据的分析进一步说明算法的有效性。表2中分别记录了每个算法在30次独立运行中获得的最优的最终函数值、平均最优函数值、中位值和标准差以及每个算法相对于本文提出的新算法GAD所获结果t-检验值。通过对平均最优值和最小的最优值的比较可以看出本文提出的算法在11个函数中能够得到相比于其他算法更优秀的解。在其他函数上得到的解和其他算法得到的最优解相差不大。

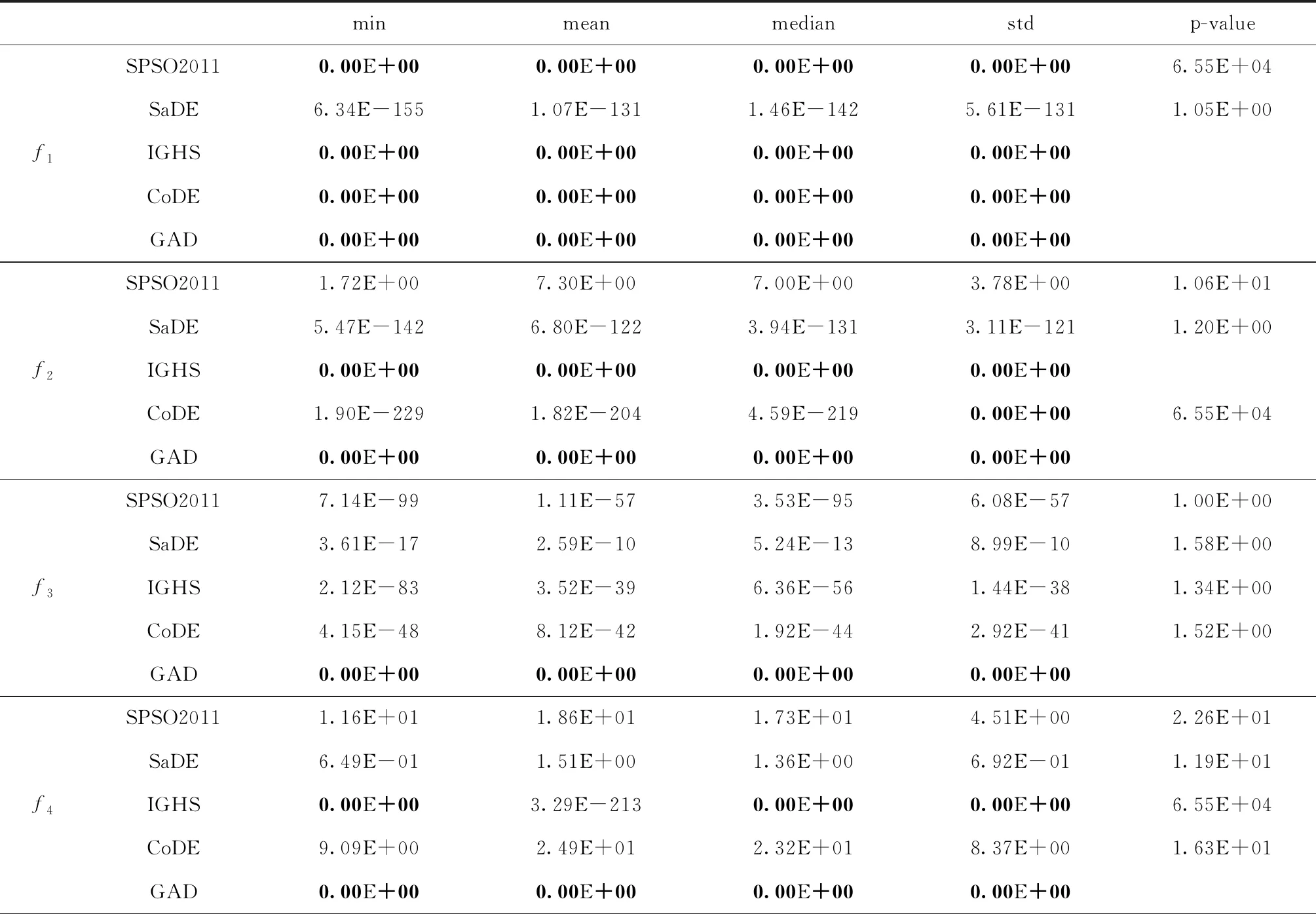
表2 SPSO2011,SaDE,IGHS,CoDE和GAD算法结果比较

续表2

续表2

通过表2可以看出相较于其他算法，本文提出的聚散优化算法无论在获得最优解的数量还是求解的精度上都具有更大的优势。其中算法GAD对CEC2014中的复合函数取得的结果更加优秀而稳定，其原因是本文对单纯形算法的引入和延伸，表明该算法有求解复杂问题中的巨大潜力。观察表格中的标准差可以看出，聚散算法的标准差往往较小于其他算法，说明在多次运行的过程中，算法得到的解更加稳定，因而具有更好的算法稳定性。观察中位数和平均值，两者的差值往往小于其他算法，进一步说明了算法的稳定性比较好。综合以上两个指标的分析可以看出，虽然本文提出的聚散优化算法GAD本质说上是一种随机优化算法，但算法GAD在实现较好搜索的同时，能够得到更加稳定的实验结果和算法性能。

4.3 实验仿真结果综合分析

表3给出了5种优化算法在求解所有优化函数上相对排名的平均结果，该数值越小表明该算法在所有测试函数上的排名越高，其综合平均性也就越好。本文提出的聚散优化算法GAD在全体函数上的平均排名是1.65，略优于经典的多策略集成的差分算法CoDE，明显的优于标准粒子群优化算法SPSO2011、策略适应性的差分进化算法SaDE和智能和声搜索算法IGHS，进一步验证了所提策略和算法框架的有效性。

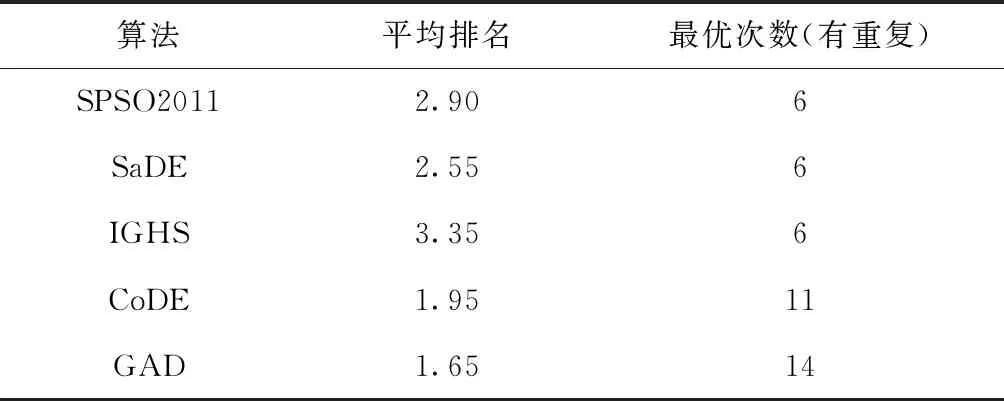
表3 SPSO2011,SaDE,IGHS,CoDE和GAD算法排名结果比较

通过仿真实验结果可以看出，本文提出的聚散搜索算子以及相应的优化算法不仅可以一定程度上保持单纯形算法本就具有的局部勘探能力，还具有群体优化算法较好的全局搜索能力，因此具有更优秀、更稳定的算法性能。

5 结束语

本文在单纯形算法的启发下，首先提出了聚集算子、分散算子和允许重复的归档重置策略，进而提出了聚散算法。通过比较聚散算法与几个经典优化算法在求解20个测试函数时的性能指标，说明了聚散算法的有效性和稳定性，尤其是对复杂函数的求解表现出巨大潜力，从而在进化算法中引入确定性优化思想的可行性与有效性。允许重复的归档重置策略使算法记录每次迭代中的有益信息，并且利用当前信息引导新的种群的生成，实质上是在算法的不同代之间进行搜索消息的传递与分享，对算法的进化方向进行宏观调控。通过将算子进行种群化调整，成功地将传统局部搜索的方法拓展成了全局搜索算法，这也初步显示了种群化是一种将传统方法全局化拓展的有效方式。未来将尝试将其他传统的优化方法包括基于梯度的方法进行种群化，以期赋予更多具有较强局部搜索能力的传统优化方法以一定程度的全局搜索能力，从而提升相应算法的性能。