考虑非固定提前期的生产计划和预防性维护联合优化模型

黄剑秋，王丽亚

(上海交通大学 机械与动力工程学院工业工程系，上海 200240)

0 引言

生产计划和设备维护计划是两项非常重要的活动，然而现有企业采用的方法大多是由生产部门和设备维护部门各自进行生产计划和设备维护计划。这种分开各自计划的方式带来的问题是，生产计划在执行时缺乏可行性或难以实施，而设备维护计划由于没有考虑生产任务引起的设备负荷的改变，往往过于粗放，导致过度维护或维护不足，从而增加生产和维护的总成本。因此，考虑生产计划和维护计划相互制约，对整个系统进行联合建模，使得生产计划和维护计划整体最优尤为重要。近年来，已有学者开始研究生产计划与预防性维护的联合优化问题[1-3]，这类联合优化模型主要基于经典的有限产能批量计划问题(Capacitated Lot-Sizing Problem, CLSP)构建。赵世雄等[4]采用循环迭代的算法研究了单机情况下的生产和维护的联合优化问题；蓝天皓等[5]、张岳君等[6]以生产和维护总成本为优化目标建立了单机情况下的生产批量和预防性维护模型；Zhou等[7]详细探讨了串行无重入的系统联合优化建模过程，建立了预防性维护和调度的联合优化模型；刘学娟等[8]考虑多产品情况下的生产计划和预防性维护联合优化建模；张博文等[9]进一步考虑并行机系统，同样以系统生产和维护的总成本为优化目标建立联合优化模型，然而这些研究都是基于固定提前期(Fixed Lead-time, FL)假设而建立的联合优化模型。固定提前期假设下制定的生产计划在设备负荷水平较高、波动较大的生产系统如半导体晶圆制造这类具有高度重入特性和高设备利用率的复杂系统中往往缺乏可行性。针对这类系统，学者们开始运用非固定提前期函数(Clearing Function)模型来解决生产计划中提前期的变动性问题[10]。非固定提前期函数的概念最初由Graves[11]提出，Karmarkar[12]紧接着提出了凸饱和的非固定提前期函数概念。在此基础上，Asmundsson等[13]考虑产品组合中每个产品的在制品(Work in Process, WIP)对提前期的影响提出了非固定提前期分派函数(Allocated Clearing Function, ACF)的概念，他们验证了在变动需求和高设备利用率环境下，由ACF构建的生产计划模型在计划准确度方面要优于传统的固定提前期的生产计划模型[14]。然而，现有关于非固定提前期函数的研究中，并没有考虑预防性维护对生产计划的影响。实际上，预防性维护和生产计划相互制约、相互影响，共同决定了生产的提前期。因此，在建立非固定提前期函数时考虑预防性维护的影响将更加符合实际。

本文针对具有重入的串行系统的复杂特性，通过仿真模型来捕获预防性维护对于生产计划的影响，建立考虑了预防性维护的非固定提前期函数(Clearing Function with Preventive Maintenance, CFPM)，并基于该函数提出一种生产计划和预防性维护联合优化模型。通过生产线不同复杂程度和设备劣化水平下的鲁棒性实验验证了该联合优化模型比现有模型能够得到更低的总成本。

1 问题描述

考虑以下具有重入的串行系统中生产计划和预防性维护的联合优化问题，该系统需加工G种类型的产品，包含M台设备。计划期包含P个等长的时间段。由于重入的原因，一个工件可能多次访问某台设备，产品g从原材料投入到产出，需经过工序集合Lg={l:m}的加工才能完成，m为工序l对应的设备。产品g每周期期末的需求为dpg，生产超出需求将产生库存成本，不满足需求将产生缺货成本，并累积到下一周期。每台设备前都有一个缓冲区，缓冲区的容量无限。系统中所有工序和产品的加工时间均相同。设备上的工件一旦加工完成，将立即进入下一道工序对应设备的缓冲区中。为方便研究，本文提出的模型基于如下假设：

(1)假设系统中所有设备均会发生随机故障，设备发生故障过程相互独立，故障率服从威布尔分布。

(2)假设设备可靠性随着时间发生劣化。当设备发生故障时，执行最小维修，即仅仅使得设备恢复工作而不改变其故障率分布和役龄。

(3)假设系统采用非周期性的预防性维护策略[15-16]。决策者需在每个生产周期期初决定是否进行维护。若进行预防性维护，则设备恢复如新，设备役龄更新为0，否则，设备役龄不变。

(4)假设系统的调度规则是基于比例的先进先出调度规则：由于串行系统中的重入特性，在同一设备缓冲区中的待加工工件可能处在加工工序不同环节。因此，按照缓冲区中工件类型比例分配设备产能。

2 联合模型建立

2.1 CFPM函数建立

在生产与维护的联合优化模型中，非固定提前期函数将负荷引入到生产计划模型的决策变量空间中，且非固定提前期函数作为一个产能约束条件参与生产计划模型的构建。Kacar等[17]和Albey等[18]对非固定提前期进行了大量的研究，本文在他们的仿真模型基础上，考虑预防性维护活动，通过建立带有预防性维护的多产品生产仿真模型，得到预防性维护对非固定提前期函数的影响，期望故障次数作为预防性维护对于生产系统影响的指标被纳入CFPM函数的变量中，从而建立考虑了预防性维护的非固定提前期函数CFPM。

本文的多产品生产仿真系统采用与Albey等[18]一致的建模过程，系统中包含三台加工时间和劣化性质相同的设备，设备编号分别1，2，3。每个设备前有一个容量可以视为无穷大的缓冲区。需加工A，B两种产品，两种产品的加工时间相同，生产的两种产品的产品组合为1:1，其加工工序对应的设备如表1所示。产品A共有5道工序，需要在设备1、2上各进行一次重入加工。产品B共有4道工序，仅在设备1上进行一次重入加工。

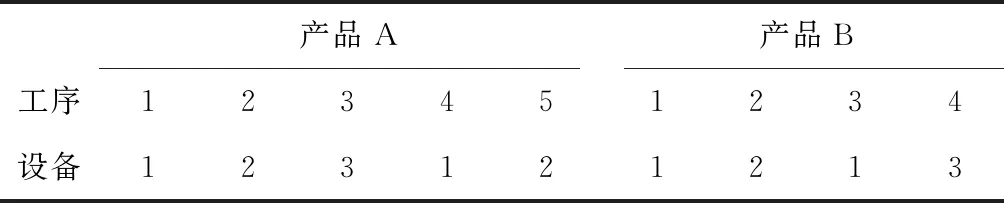
表1 两种产品的设备和工序对应

生产计划一个周期长度为7天，设备的故障过程服从二参数威布尔故障分布，其中形状参数γ=2.08，尺度参数θ=10 000。设备发生故障时需进行故障维修，维修时间为800 min，预防性维护所需时间为600 min。实验中总生产计划期的长度为490天，仿真过程中采集每个生产计划周期内的设备平均故障次数、在制品数和产出数据。为了消除随机误差，实验重复20次。仿真过程中得到的在制品数、设备平均故障次数以及产出数据绘制在三维坐标图中，考虑了预防性维护的非固定提前期函数的图像如图1所示。

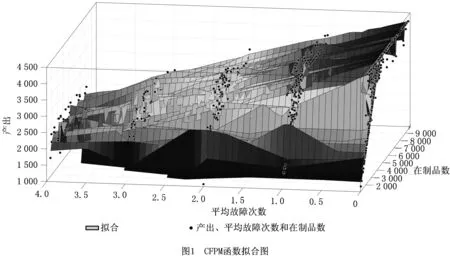
对该图像的数据使用分段线性回归，得到考虑维护的非固定提前期函数CFPM的通用形式：

TP=A*WIP+C*Np+D。

(1)

式中：TP表示系统产出；WIP表示在制品数；Np表示设备的期望故障次数；A、C、D是回归参数。

2.2 联合优化模型(CFPM-M)建立

建立考虑预防性维护的非固定提前期函数CFPM后，以现有非固定提前期函数生产计划模型为基础，将CFPM函数引入生产计划模型，从而建立生产计划与预防性维护的联合优化模型(Joint Optimization Model with CFPM, CFPM-M)。

(1)索引和集合

g为产品标号,g=1,2,…,G,G为产品总数量；

m为设备标号,m=1,2,…,M,M为设备总数量；

p为周期标号,p=1,2,…,P,P为周期总数量；

l为工序标号,l=1,2,…,Lg,Lg为产品g的工序集合。

(2)决策变量

Wgpl为计划周期p内产品g在工序l上等待加工的产品数量；

Igp为计划周期p结束时产品g的库存量；

Bgp为计划周期p结束时产品g的缺货积压量；

Rgpl为计划周期p内产品g在工序l上的投料量；

Rgp为计划周期p内产品g的投料量；

Xgpl为计划周期p内产品g在工序l上的产出量；

Xgp为计划周期p内产品g的产出量；

Np为计划周期p内设备的期望故障次数；

Zp为维护决策变量，如果在计划周期p开始时对设备进行预防性维护，Zp=1；否则，Zp=0。

(3)参数

T为周期时长；

i为非固定提前期函数分段线性回归时变量负荷被分割的段数；

j为非固定提前期函数分段线性回归时变量Np被分割的段数；

aij为非固定提前期函数分段线性回归时变量负荷的回归系数；

yij为非固定提前期函数分段线性回归时的截距；

cij为非固定提前期函数分段线性回归时变量Np的回归系数；

ωgpl为计划周期p内单位产品g在工序l上的单位在制品库存成本；

ru为设备的失效率函数；

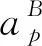
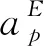
hgp为计划周期p内单位产品g的单位库存成本；

bgp为计划周期p内单位产品g的单位缺货积压成本；

xgp为计划周期p内单位产品g的单位生产成本；

kgp为计划周期p内生产单位产品g的时间；

dgp为计划周期p内单位产品g的需求；

s0为预防性维护的单位成本；

q0为预防性维护的单位时间；

se为维修的单位成本；

qe为预防性维护的单位时间。

联合优化数学模型表述如下：

minimizeTC=TPC+TMC,

(2)

(hgpIgp+bgpBgp),

(3)

(4)

s.t.

Ig,p-1+Xgp+Bgp-Bg,p-1-Igp=dgp,

∀g,p;

(5)

Wgpl=Wg,p-1,l-Xgpl+Rgpl,∀g,p,l;

(6)

(7)

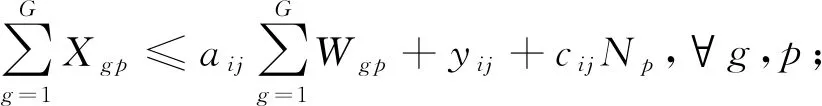
(8)

(9)

(10)

(11)

Wgpl,Igp,Bgp,Xgp,Rgp,Np,Zp≥0,∀g,p,l。

(12)

该模型以生产和维护的总成本为优化目标，其中：式(2)是该模型的目标函数，表示总成本由生产计划成本与设备维护成本组成；式(3)表示生产计划相关的总成本；式(4)表示维护成本包含预防性维护和故障维修成本两部分；式(5)表示各周期内的库存平衡等式；式(6)表示各周期内的WIP平衡等式；式(7)和式(8)为产能约束，式(7)表示设备的额定产能减去预防性维修和故障时间为可用于生产的产能；式(8)表示生产可用产能还需要满足非固定提前期函数约束，考虑预防性维护下的非固定提前期函数CFPM由2.1节介绍的线性回归得到；式(9)表示设备的期望故障次数；式(10)表示设备周期初、周期末的役龄关系；式(11)表示设备役龄周期初和上一周期末之间的关系；式(12)表示各决策变量的非负约束。

3 数值实验与模型验证

为了说明联合优化模型(CFPM-M)的有效性，将联合优化模型和Asmundsson等[13]的带ACF的生产计划模型(ACF-M)以及赵世雄等[4]的带预防性维护的固定提前期模型(FL-M)在生产线不同复杂程度和劣化水平下进行对比。

(1)带ACF的生产计划模型(ACF-M)

带ACF的生产计划模型中的生产计划部分是由Asmundsson等[13]提出的没有考虑预防性维护影响的非固定提前期函数模型。为了使得模型具有可比性，ACF-M模型在ACF模型基础上增加了预防性维护模型：

Minimize 式(2)～式(4)。

s.t.

约束式(5)～式(7);

(13)

约束式(9)～式(12)。

该模型以生产和维护的总成本为优化目标，目标函数式(2)～式(4)与CFPM-M模型一致。式(13)表示产能约束，生产可用产能需要满足非固定提前期函数约束，没考虑预防性维护下的非固定提前期函数ACF由Asmundsson等[13]给出；约束式(5)～式(7)，式(9)～式(12)与CFPM-M模型一致。

(2)带预防性维护的固定提前期模型(FL-M)

带预防性维护的固定提前期模型使用的是赵世雄等[4]提出的固定提前期下的生产计划与维护计划联合优化模型：

Minimize 式(2);

(14)

式(4)。

s.t.

约束式(5);

约束式(7)～式(11);

Igp,Bgp,Xgp,Rgp,Np,Zp≥0,∀g,p。

(15)

该模型以生产和维护的总成本为优化目标，目标函数中式(2)和式(4)与CFPM-M模型一致，式(14)表示生产计划相关的总成本。约束式(5)，式(7)～式(11)与CFPM-M模型一致；式(15)表示各决策变量的非负约束。

3.1 模型求解

经典的CLSP、ACF问题已经被证实是NP-hard问题，求解十分困难。而联合优化模型CFPM-M模型是在ACF问题基础上建立的，且维护计划部分存在积分是一个非线性问题。综上所述，所建立的CFPM-M模型是一个复杂的非线性混合整数规划问题。由于求解该模型比较复杂，对式(10)进行了简化处理：

(16)

计算时假设设备失效是基于时间失效的，该方法将造成精度损失，但会大大降低求解难度。由于简化后的模型中预防性维护变量是0-1变量，可以事先确立预防性维护。预防性维护变量确立后，模型将转化为混合线性规划模型，可以利用CPLEX、Matlab、Lingo等商业软件进行求解。

3.2 算例分析

表2 各产品生产类成本参数

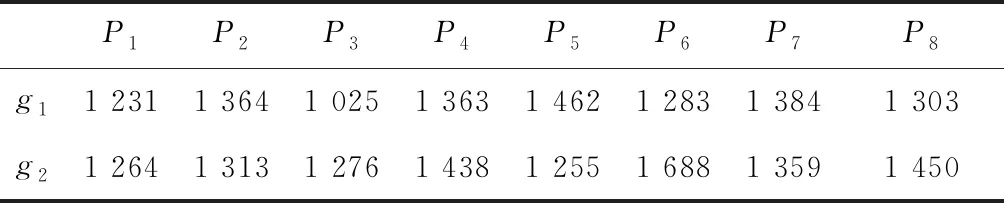
表3 各产品生产类需求参数

表4为算例求解结果，可以看出该组参数下总成本主要由产品g2的缺货成本和维护成本构成。

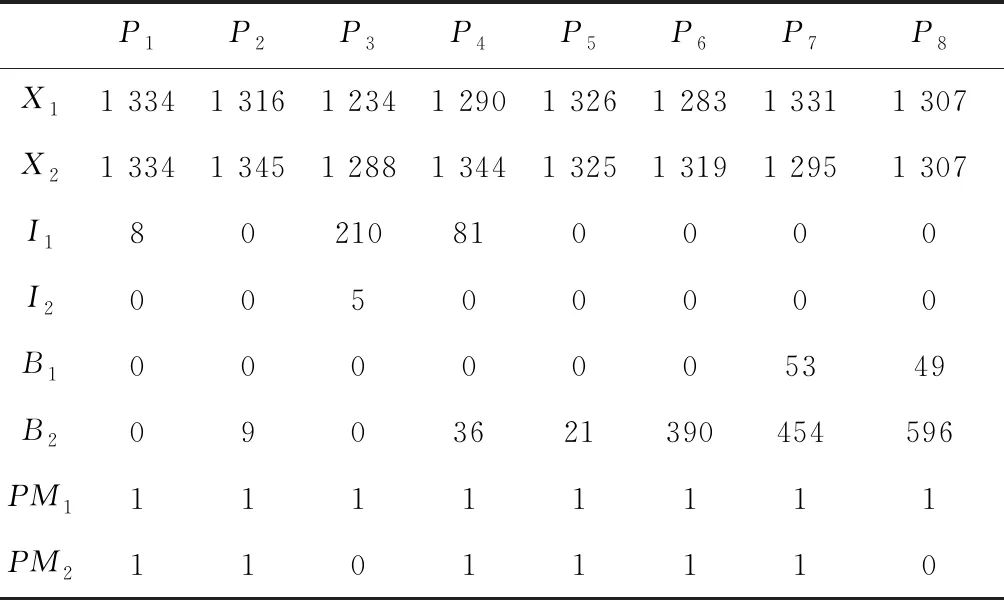
表4 算例求解结果

3.3 生产线复杂程度分析

本文所建立的联合优化模型是对真实系统的抽象简化，为进一步研究本文提出的联合优化模型相较于现有生产计划模型的性能表现，设置了生产线不同复杂程度下的数值实验。生产线中设备数量增加时，设备维护的解空间将会呈指数级增长，此时设备预防性维护决策对生产的影响较大。相比于简单的无重入串行系统，具有重入的串行系统设备前的待加工工件可能来自于多道工序，更优的生产计划决策安排将减少在制品量的堆积，从而减少总成本。针对生产线不同复杂程度，本文将研究设备数量、串行系统是否重入这两种因素下，3种生产计划模型的性能表现。

考虑系统需加工A、B两种产品，生产计划期的长度为16周，设备和成本相关参数与算例分析中的相同，需求服从均值为1 230，标准差为0.1的正态分布，在该需求水平下，设备的平均利用率为80%。

(1)少设备 3台设备，实验标记为F；

(2)多设备 9台设备，实验标记为M；

(3)重入串行系统 实验标记为R，在3台设备的重入串行系统中，工序与设备的对应关系与2.1节中相同，而在9台设备情况下对生产线做了平衡处理，设备和工序对应如表5所示;

表5 两种产品的设备和工序对应

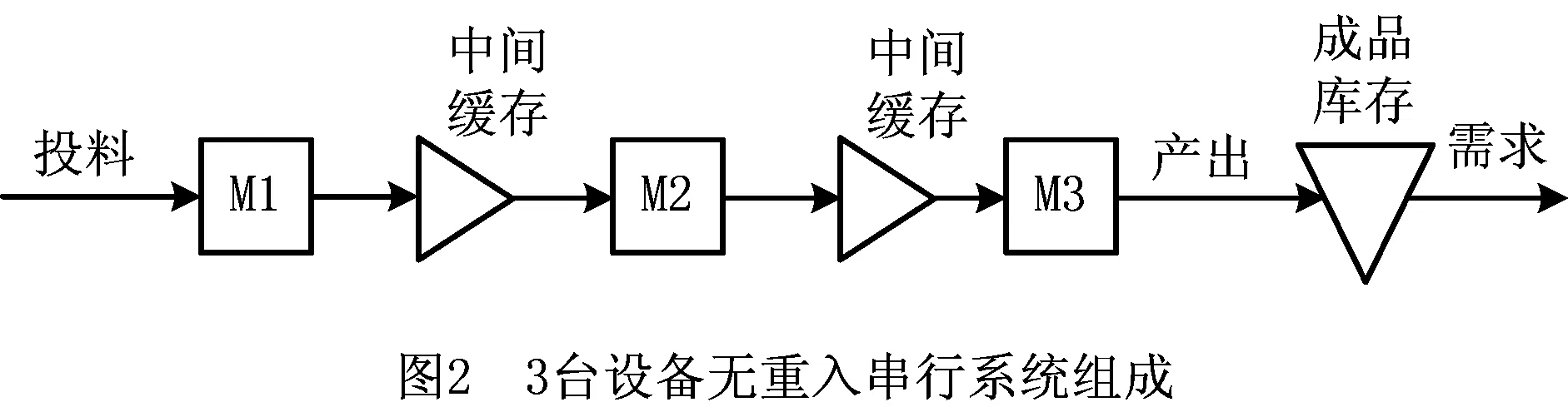
(4)无重入串行系统 实验标记为S，3台设备无重入串行系统如图2所示，一道工序只能在一个设备上加工，一个设备只能加工一道工序。

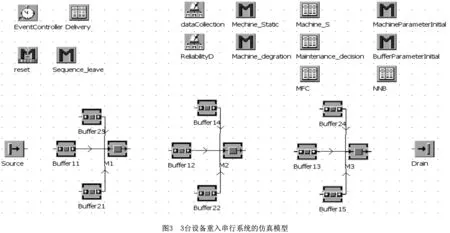
图3为3台设备重入串行系统的仿真模型。重复运行仿真模型15次后得到每个周期系统的平均产出和平均故障次数，由此得到3个模型的实际运行总成本。

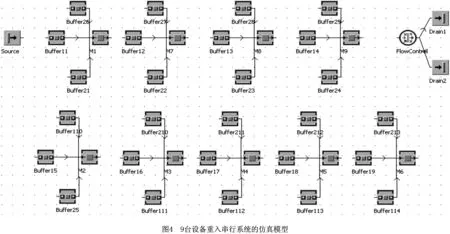
在9台设备重入串行系统中，设备数量增加了6台，A、B两种产品的工序数也分别增加到了原来的3倍，每台设备前的缓冲数量保持不变。图4为9台设备重入串行系统的仿真模型。在九台设备无重入串行系统中，设备参数和3台设备模型相同。

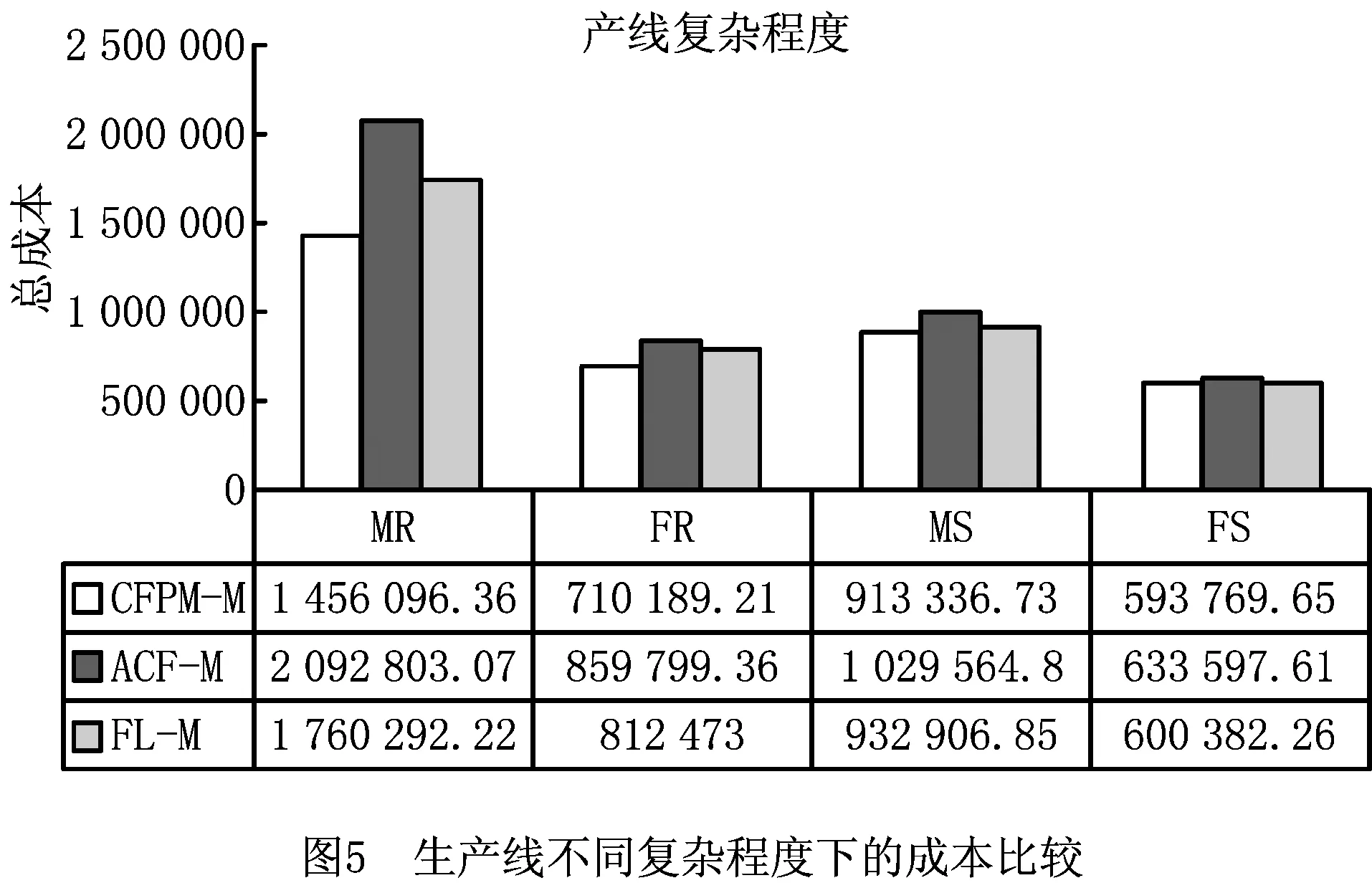
如图5所示为3种模型在4种生产线复杂程度下的成本比较，从仿真结果看，CFPM-M在各组实验下的成本均最低，FL-M的总成本低于ACF-M。在9台设备重入串行系统中，CFPM-M的成本比FL-M低17.2%，比ACF-M低30.4%。在3台设备重入串行系统中，CFPM-M的成本比FL-M低12.6%，比ACF-M低17.4%。联合优化模型真正对生产计划和预防性维护的耦合进行建模，会使得系统的产能利用更合理，避免生产资源浪费，以达到更小的总成本。FL-M采用了固定提前期假设，而在重入系统中，不断的重入工序造成设备负荷较高，生产提前期变长，FL-M得到的生产计划往往缺乏可行性，使得总成本更高，且设备数量越多，生产线越复杂，这种结果越明显。虽然Kacar等[14]研究表明非固定提前期ACF模型相比于固定提前期FL模型能够得到更优的生产计划，但是ACF-M没有考虑预防性维护对于生产计划的影响，生产计划难以执行，也导致了总成本高。因此，针对具有重入的串行生产系统需要考虑非固定提前下生产和维护的联合优化建模。

在9台设备无重入串行系统中，CFPM-M的成本比FL-M低2%，比ACF-M低11%，在3台设备串行系统中，CFPM-M的成本比FL-M低1%，比ACF-M低6%。在无重入的串行系统中，生产提前期受到影响较小，联合优化模型CFPM-M相比于固定提前期模型FL-M的优势没有重入系统中明显，说明在重入系统中需要考虑非固定提前期。同样，ACF-M相较于FL-M，由于没有考虑预防性维护对于生产计划的影响，总成本更高。且生产系统复杂程度越高，CFPM-M的优势越明显。通过与串行系统的对比，进一步说明本文建立的联合优化模型更加适用于具有重入的串行生产系统。

3.4 劣化速度参数分析

在现实系统中，设备由于生产负荷、机械特性的关系，会出现不同的劣化特性，本文对不同设备劣化速度下3种生产计划模型的性能进行分析。假设设备的劣化速度只由尺度参数θ决定，考虑θ分别为7 200、10 000和14 400时生产计划模型的表现。当θ=7 200时，设备的劣化最快，θ=14 400时，设备的劣化最慢。

以3台设备重入串行系统为研究对象，研究3种模型在不同设备劣化速度下的表现。约定恒定需求，实验标记为C；变动需求，实验标记为V；设备高利用率时，设定设备利用率为90%，实验标记为H；设备低利用率时，设定设备利用率为70%，实验标记为L。分别对3种劣化尺度参数、4种需求模式(VH、VL、CH、CL)下的CFPM-M，ACF-M和FL-M模型进行求解与仿真实验。设备利用率高则设备负荷水平高，设备劣化速度也快。

图6分别为4种需求模式下，劣化速度不同时3种模型的成本分布情况。其中：B为缺货成本，HC为库存成本，W为在制品库存成本，PM为维护成本，CM为故障成本。

结果显示，设备劣化速度加快时，在制品库存成本占总成本的比重将会增加，固定提前期模型FL-M在设备劣化速度加快时相较于其他两个模型成本增加更明显。3种模型在变动需求和恒定需求下的表现差异性并不明显，说明外部需求变动对于联合优化模型的稳定性干扰较小。在低利用率时，3种模型在不同劣化速度下的差异性可忽略。但是在高利用率时，无论恒定需求，还是变动需求，联合优化模型CFPM-M和FL-M以及ACF-M的总成本差异明显，表明联合优化模型更适用于劣化速度快、设备利用率高的重入系统。同时，通过总成本对比，表明联合优化模型可以对生产资源进行合理配置，使系统整体最优。

4 结束语

本文研究了一种考虑非固定提前期和预防性维护的生产计划联合建模问题。考虑了预防性维护和生产计划之间相互影响的关系，建立了生产计划和预防性维护联合优化数学模型。针对不同设备数量、有无重入生产线以及不同劣化速度3种情况，本文对比并分析了非固定提前期的联合优化模型、带ACF的生产计划模型和固定提前期的联合优化模型的表现。结果表明，本文提出的非固定提前期的联合优化模型在利用率较高且有重入的复杂系统中具有最佳性能，当设备劣化较快时，所建立的联合优化模型具有优势，从而验证了本模型在具有重入的串行系统中的实用性以及联合优化模型能够实现更切合实际情况的生产计划和维护计划，降低生产总成本。未来可考虑更加复杂的带批处理的重入串行系统的联合优化模型研究，探索更加合理的模型简化求解方法。