基于制造商回收的双渠道闭环供应链博弈分析
司凤山,王 晶,戴道明
(安徽财经大学 管理科学与工程学院,安徽 蚌埠 233030)
0 引言
随着绿色经济和循环经济的发展,废旧产品的回收利用已成为减少环境污染和降低制造成本的有效途径。制造商在经营双渠道销售的同时,也在积极开拓回收渠道,从而形成双渠道闭环供应链。
关于双渠道闭环供应链中第三方回收的策略问题,学者们从公平关切下的决策均衡[1]、集中和分散决策下的最优决策方案及协调机制[2-4]、歧视性回收与公平回收策略[5]、零售商和第三方回收对比分析[6]等方面分析了第三方回收对双渠道闭环供应链利润和回收率的影响,给出了供应链绩效的评价标准。
关于消费者对再制造产品的偏好和提供废旧产品的意愿问题。学者们研究了双渠道闭环供应链中Stackelberg和Bertrand博弈模式下消费者偏好对定价和协调策略的影响[7]、政府补贴对象的不同及消费者偏好的差异对最优决策的影响[8]、消费者对再制造产品的接纳程度,以及消费者对直销渠道的偏好对闭环供应链定价和利润的影响[9]、提供折扣或直接费用对消费者提供废旧产品意愿的影响[10]等问题,研究成果为政府制定补贴和免税政策及实施供应链协调提供了参考依据。
针对市场的需求不确定性和渠道权利结构差异问题,倪明等[11]在考虑需求不确定基础上,分析了3种回收模式下的最优决策解问题,并对3种回收模式进行了比较分析;李向荣等[12]研究了在市场需求变动的情况下,双渠道闭环供应链在集中决策和分散决策模式下的价格博弈策略问题,给出了最优定价策略;李明芳等[13]研究了在制造商负责回收的闭环供应链中,基于4种渠道权利结构下的最优决策问题,给出了不同结构下最优决策的比较分析结果;林杰等[14]研究了双正向和双逆向物流并存的供应链中的最优定价策略问题,分析了制造成本和渠道竞争强度对最优决策的影响,给出了不同渠道权利结构下的产品销售价格、回收价格和零售商利润的解析表达式。
针对回收比例、再制造率、再制造成本和再制造产品售价问题。Xie等[15]研究了双渠道闭环供应链中集中决策和分散决策下的契约协调问题,考虑了回收率与回收收益率之间的关系,设计了收益共享机制,给出了最优的双渠道售价、批发价和广告投资;朱晓东等[16]考虑线下回收和线上回收两种渠道之间的成本和可再制造比例,分析了竞合决策模式下的最优回收价格和利润,探究了回收竞争系数、可再制造比例等因素对最优策略的影响,并借助收益共享合同实现了供应链协调;李晓婧等[17]在考虑碳交易和碳排放的基础上,分析了双渠道闭环供应链模型的网络均衡问题,给出了再制造率、原材料转化率等决策参数的最优解以及网络均衡的条件;张成堂等[18]在考虑再制造产品售价差异和多种旧产品回收渠道的基础上,分析了最优的产品售价和回收价策略,在多渠道回收机制的基础上,利用收益共享机制实现供应链协调。
另外,学者们还对闭环供应链中的联合决策、消费补贴、专利许可、碳减排技术和风险合同等问题展开了研究。王玉燕[19]研究了存在双渠道回收机制的闭环供应链,给出了不同决策模式的最优策略解析式,并讨论了有无政府干预、是否联合决策等因素对最优策略的影响;Ma等[20]研究了政府的消费补贴对双渠道闭环供应链的影响,分析了政府资助计划前后的渠道成员策略,从消费者、闭环供应链的规模和企业的角度分析了消费补贴对最优策略的影响;郑本荣等[21]研究了双渠道闭环供应链中,考虑专利许可的博弈模型的最优定价和协调策略,讨论了集中和分散决策模式下的供应链成员利润均衡解,通过改进的收益共享合同实现对供应链的协调;张杰芳等[22]研究了二级闭环供应链中碳减排技术对最优决策的影响及协调问题,给出了最优策略的解析表达式;He[23]设计了供应风险分担合同下、供过于求风险共享合同、完整的供应风险分担合同和无风险分担合同对闭环供应链的协调作用,并分析了不同合同对产品回收价格和回收数量的影响。
综上所述,学者们从多方面、多角度对双渠道闭环供应链最优决策问题进行了研究,使用优化的方法给出了最优决策的解析表达式。但是,研究内容上同时涉及回收率和再制造成本差异的文献并不多见,研究方法略显单一。因此,本文在考虑产品回收率和再制造成本差异的基础上,对基于制造商回收的双渠道闭环供应链中的最优策略和动力学演化博弈行为进行研究。与以往文献相比,在研究内容上综合了回收率和再制造成本差异两个关键决策因素;在研究方法上,一方面构建了单周期静态博弈模型,通过优化的方法给出决策的最优解,另一方面建立了时滞动态博弈模型,借助非线性动力学理论和系统复杂性理论分析了系统的演化过程,给出了多种因素对系统稳定性和复杂性的影响,实现了对失稳系统的有效性控制。
1 问题描述与基本假设
1.1 问题描述
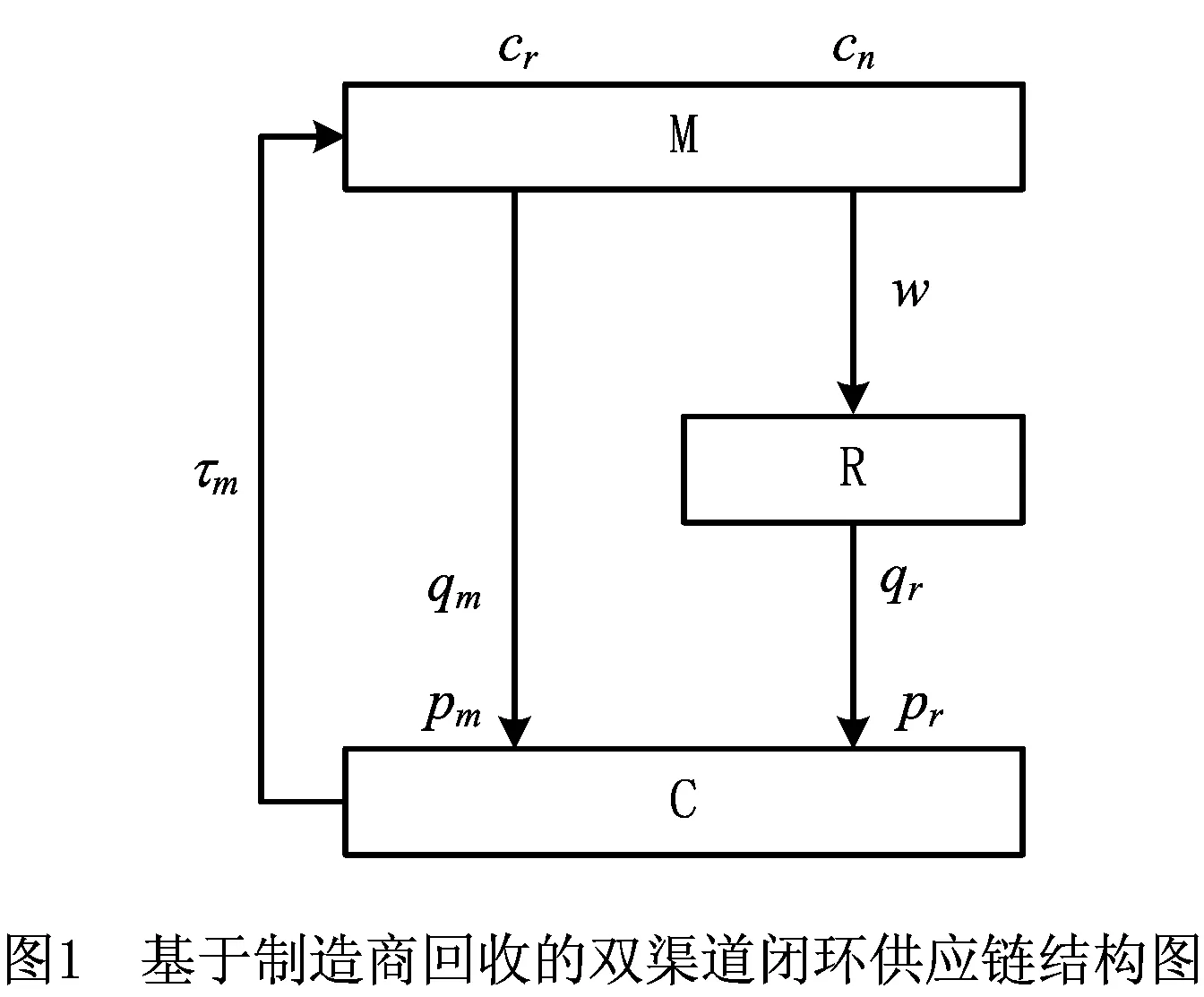
在双渠道闭环供应链中,产品回收率和再制造成本差异会对最优决策产生较大影响,基于制造商回收的闭环供应链结构如图1所示。其中,制造商一方面利用原材料生产新产品,单位新产品的生产成本为cn,另一方面还直接从消费者手中回收废旧产品进行再制造,废旧产品的回收率为τm,单位再制造产品的成本为cr。制造商生产的新产品和再制造产品,一是通过线上渠道进行网络销售,直销价为pm,二是以价格w批发给零售商进行线下渠道销售,零售价为pr。直销渠道和零售商渠道的产品需求量分别为qm和qr。
1.2 基本假设
为便于研究,对模型做出如下假设:
(1)研究的前提是市场中已经存在废旧产品,即产品已处于循环利用中。

(3)制造商回收的废旧产品全部用于再制造。通常情况下,再制造产品在质量上与新产品还存在差异,但是由于其具有价格优势,消费者仍然对其有一定的购买意愿。因此,新产品和再制造产品能够同时在双渠道中进行销售,形成渠道间的价格竞争。
(4)单位再制造产品的成本小于单位新产品的制造成本,即cr (5)单位产品的生产成本c由再制造产品的单位成本cr和新产品的单位成本cn按回收率的比例构成:c=τmcr+(1-τm)cn=cn-τmΔ。 直销渠道和零售商渠道的产品需求量分别为: qm=a-β1pm+γ1pr, (1) qr=a-β2pr+γ2pm。 (2) 其中:a>0为新产品和再制造产品的最大潜在需求量;β1,β2>0为需求量对自身价格的敏感系数;γ1,γ2>0为需求量对交叉价格的敏感系数。为了简化运算,参照文献[25],此处假定β1=β2=β,γ1=γ2=γ。由于渠道的需求量对自身价格的依赖程度高于竞争渠道的价格,故而β>γ。 集中决策下的供应链系统利润为: πc(pm.c,pr.c,τm.c)=(pm.c-cn+τm.cΔ)qm.c+ (3) 式中:πc为集中决策下的系统利润,下标c表示集中决策。 (4) (5) (6) 证明经计算,πc(pm.c,pr.c,τm.c)关于pm.c、pr.c和τm.c的Hessian矩阵为 因为一阶主子式Det(H11)<0,二阶主子式Det(H12)=4(β2-γ2)>0,当η>(β-γ)Δ2时,三阶主子式Det(H13)<0,此时Hessian矩阵H1是负定的,所以πc(pm.c,pr.c,τm.c)是关于pm.c、pr.c和τm.c的严格凹函数,即πc(pm.c,pr.c,τm.c)存在最大值。 命题1得证。 此时,集中决策下供应链的最优系统利润为 (7) 证明 命题2得证。 在分散决策下,制造商和零售商以各自利润最大化为决策目标。考虑到制造商和零售商在博弈过程中所处的地位,此处研究制造商为主导的Stackelberg博弈。其中:制造商是领导者,优先决定直销价pm.s、批发价ws和回收率τm.s;零售商是跟随者,在制造商决策的基础上再决定零售价pr.s。此时,制造商和零售商的利润分别为: πm.s(pm.s,ws,τm.s)=(pm.s-cn+τm.sΔ)qm.s+ (8) πr.s(pr.s)=(pr.s-ws)qr.s。 (9) 其中:πm.s和πr.s分别为制造商利润和零售商利润;下标s表示Stackelberg博弈。 (10) 根据式(1)、式(2)、式(8)、式(10)可得πm.s(pm.s,ws,τm.s)关于pm.s、ws和τm.s的Hessian矩阵为 (11) (12) (13) 由式(10)~式(12)可得最优零售价为 (14) 命题3得证。 此时,制造商和零售商的最优利润分别为: (15) (16) 证明证明过程与命题2类似。 为了更好地验证命题2和命题4结论的正确性,参数取值如下:a=1.2,β=0.6,γ=0.5,cn=0.6,w=0.8,η=0.5。 (1)在命题2中,条件cn=0.62 单周期静态博弈模型构建
2.1 集中决策情形

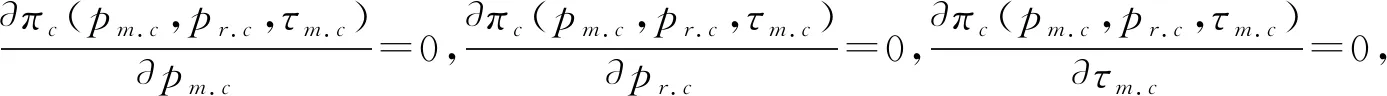
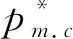
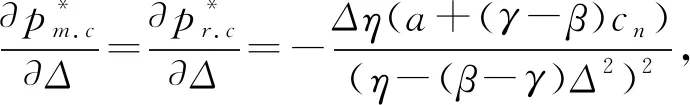

2.2 分散决策情形
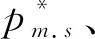
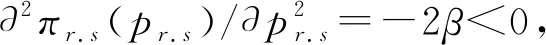
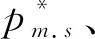
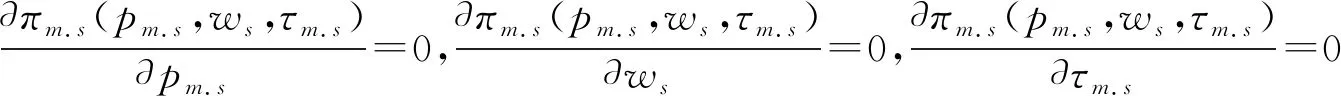
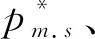
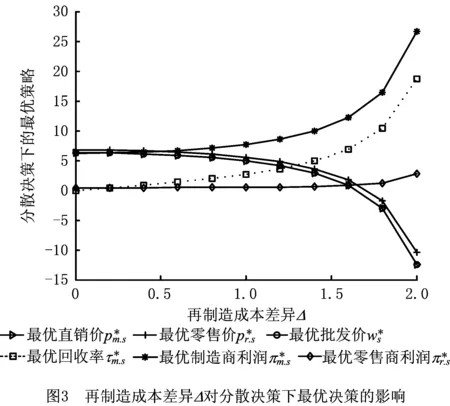
3 静态模型数值仿真