考虑刚柔耦合的工业机器人多目标可靠性拓扑优化
胡启国,周 松
(重庆交通大学 机电与车辆工程学院,重庆 400074)
0 引言
工业机器人朝着高速、高精度、重载和轻量化的方向发展,因此对其结构部件提出了更高的要求。各部件在工作过程中在其自身重量和所受载荷的作用下会发生变形,变形会转移到机器人的执行机构,造成执行机构的定位偏差。在某些对定位要求苛刻的场合,这种情况不能忽略[1]。因此,机器人在不同工况下都应具有更高的静动态特性,以减小运动过程中的变形和振动,提高末端定位精度;同时要有更小的自重,以减小运动惯量,提高整机运动速度[2]。由此可见,对于变形较大的各部件,不能视为理想刚体,有必要在对工业机器人进行刚柔耦合动力学分析的基础上进行优化设计[3]。
但在机器人结构优化分析中,由于实际工程制造误差和各种环境因素的影响,所考虑的施加载荷和结构的参数等不可避免地存在随机不确定性,从而导致机器人性能下降。为此,提出了对机器人进行可靠性拓扑优化设计。Jung等[4]将可靠性分析与拓扑优化方法相结合用于结构优化,获得更加可靠的结构性能;Bae等[5]提出了以刚度最大化为目标的可靠性拓扑优化方法,在使用同等材料的条件下得到最大的结构刚度;Zhan等[6]基于基础结构法建立了可靠性拓扑优化数学模型,得到的柔顺机构性能比确定性拓扑优化结果更优;Liu等[7]将描述拓扑优化的函数与一次二阶矩法相结合,进而获得边界光滑的材料分布且满足可靠度要求的优化方法;Jalalpour等[8]考虑到结构材料的不确定性问题,提出了有效的基于可靠性连续体拓扑优化方法。但上述文献通常将需要优化的结构体主要看成是刚性,且是针对某一部件在外部负载下的结构改进,对各部件之间耦合作用关系不够重视,为此对考虑刚柔耦合的结构可靠性拓扑优化还有待深入研究。
本文以广州数控设备有限公司RB08型工业机器人为研究对象,建立工业机器人刚柔耦合动力学分析模型,获得机械臂在不同工况下的动态载荷。考虑了结构几何尺寸、材料属性、作用载荷等随机性,采用一次二阶矩法得到臂部结构可靠性指标,再以可靠性指标为约束条件,以运用折衷规划法定义的臂部静态刚度、动态各阶固有频率及构件质量为综合的优化目标,通过层次分析法评价子目标权重系数,对臂部结构进行基于可靠性约束的拓扑优化设计。最后,通过分析结果表明了本文所提方法的正确性和有效性。
1 刚柔耦合多体系统动力学建模
利用多刚体动力学和有限元法[9]建立刚柔耦合模型。首先,基于有限元法获取机器人柔性体文件,然后对机器人各部件进行网格划分,则第i个节点的空间位置矢量为
ri=X+A(Si+φiq)。
(1)
式中:X、A分别表示局部坐标系在惯性坐标系中的位置矢量和局部坐标系原点相对惯性坐标系原点的余弦矩阵;Si为第i个节点变形前在局部坐标系中的位置矢量;φi为第i节点的模态矩阵子块;q为模态振幅向量[10]。
设X=[x,y,z]T,ψ=[φ,θ,η]T,q=[q1,q2,…,qm]T,m为模态坐标数。其中,φ、θ和η为局部坐标系原点相对于整体坐标系原点的欧拉角,qm为第m阶模态振幅的振型分量,则柔性体运动的广义坐标为
ξ=[XT,ψT,qT]T。
(2)
将式(1)对时间求导,得第i节点的速度为
(3)
式中:“~”为向量对应的对称矩阵;I为单位矩阵;B为对欧拉角求一阶导数变为角速度的转换矩阵。
由式(3)求解动能T与势能Vg的方程式为:
(4)
(5)
式中:mi为节点i的质量;M(ξ)为质量矩阵;K(ξ)为柔性体的模态刚度矩阵。
由拉格朗日方程并结合式(4)和式(5),得到机器人臂部的柔性多体运动微分方程为
(6)
式中:λ为拉氏乘子;fg为臂部的重力;D为柔性体的阻尼矩阵;Ω和Q为施加的外部载荷。
再用拉格朗日乘子法,建立第i个柔体或刚体的方程为
(7)

对式(7)的等号左边进行推导变形:
(8)
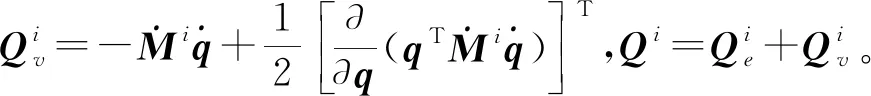
将上式简化结果代入式(7)可得
(9)
式中i为包含了柔体单元的多体系统构件个数。将式(9)与系统的约束方程C(q,t)=0(t表示时间)联立,求解即为刚柔耦合多体系统的动力学模型。
2 多目标可靠性拓扑优化方法
2.1 可靠性分析
以随机变量x=(x1,x2,…,xn)T表征结构中的不确定性因素,设定一个描述结构工作状态的功能函数g(x1,x2,…,xn),则各随机变量与结构功能状态间的关系为
(10)
式中极限状态方程Z=g(x1,x2,…,xn)=0将基本变量空间划分为失效区和安全区两个部分。设结构处于失效状态的概率为Pf,采用计算简便、效率高的一次二阶矩法求解Pf,通常将随机变量x=(x1,x2,…,xn)T映射为标准化空间的标准正态变量y=(y1,y2,…,yn)T,即
(11)
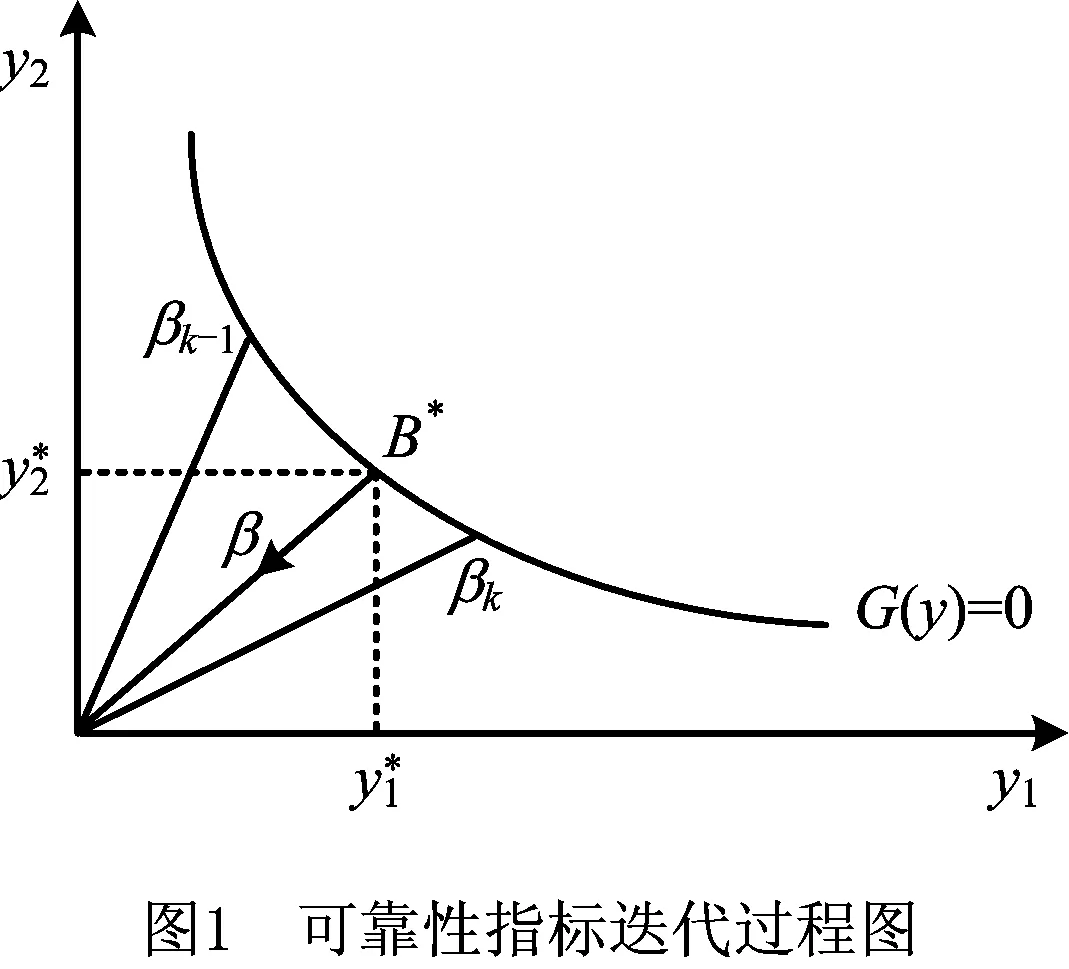
式中,yi~N(0,1),μi、σi分别为随机变量xi的均值与标准差。可靠度指标β表示为标准正态空间中从原点到失效面G(y)=0的最短距离[11]。Pf与β存在一一对应的关系:
Pf=1-Φ(β)。
(12)
式中:Φ(·)为标准正态变量分布函数,要使结构处于安全区,失效概率Pf要尽可能小,可靠度指标β要尽量大。进而可以将具有足够大的可靠度指标作为结构安全使用的约束条件,即
β≥β*。
(13)
式中β*为许用可靠度指标,可根据实际需要选择。对应许用可靠度指标约束的正态随机变量yi可根据下式求出:
(14)
s.t.
β(yi)≥β*。
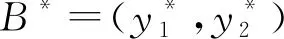
2.2 静态刚度拓扑优化模型
本文采用变密度法的插值模型[12],以体积分数及可靠度指标为约束条件、以结构柔度最小化(结构刚度最大化)为优化目标,构建结构刚度可靠性拓扑优化问题的数学模型:
findx=(x1,x2,x3,…,xn)T∈R,
s.t.
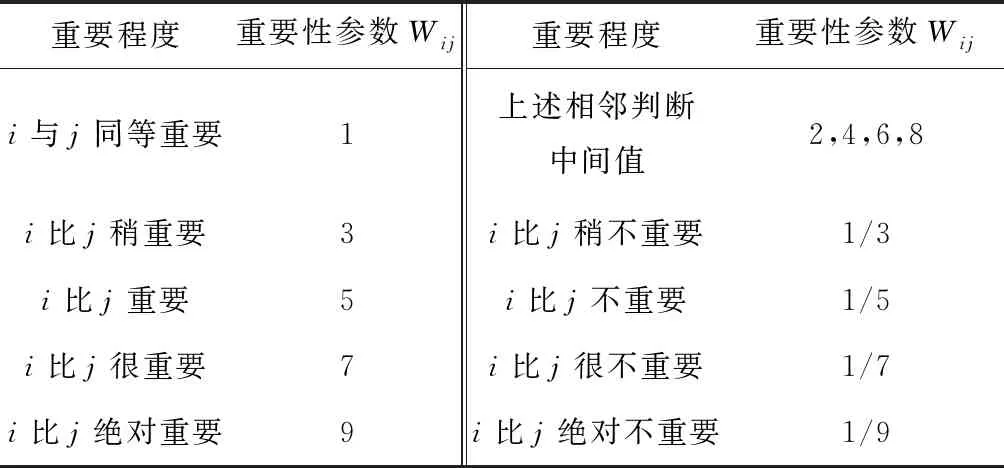
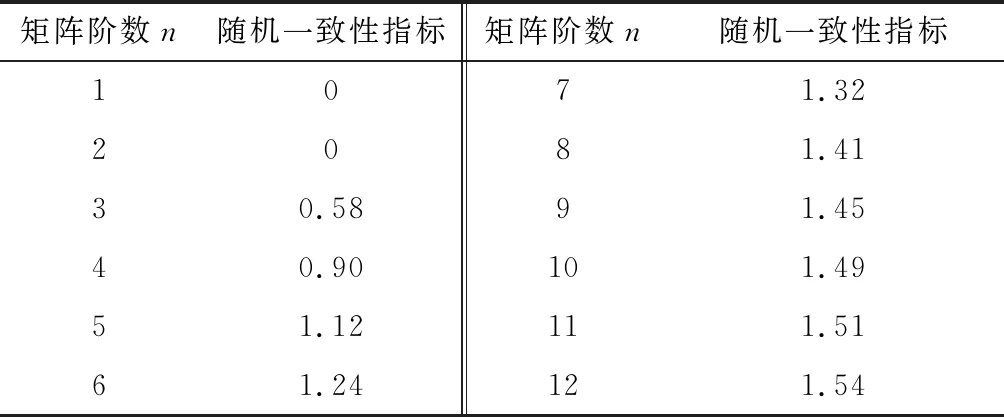
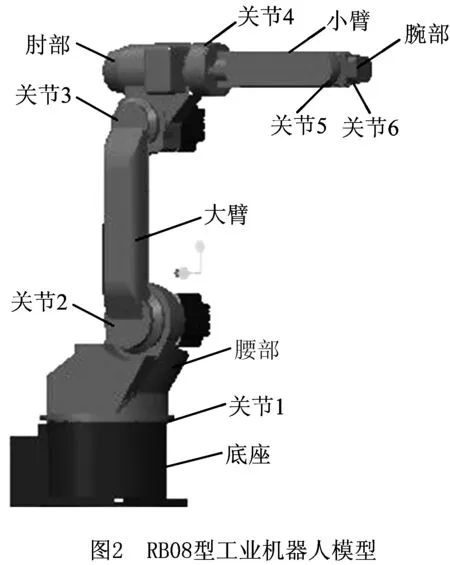
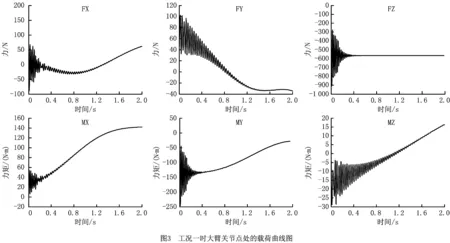
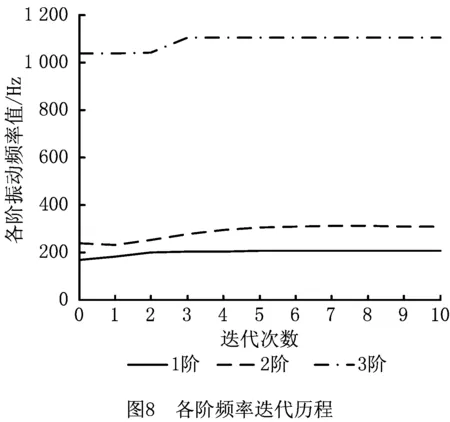
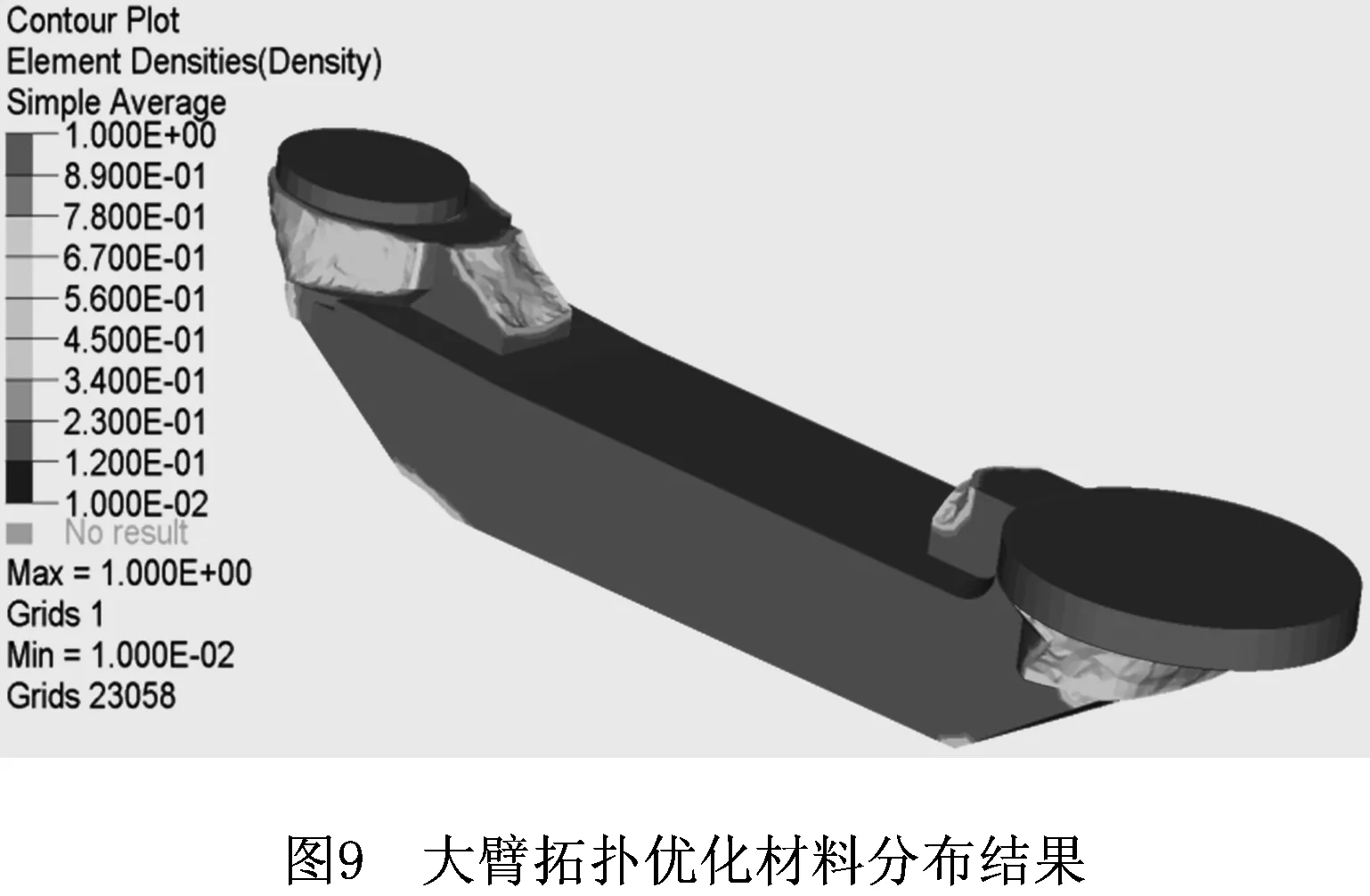
0 (15) 式中:C为结构的柔度;F为载荷矢量;U为位移矢量;K为结构刚度矩阵;ui为单元位移矢量;ki为插值后的单元刚度;p为惩罚因子;k0为初始单元刚度;vi为单元体积;V为优化后的体积;f为保留的体积分数;v0为初始体积;xmin为设计变量的取值下限;xmax为设计变量的取值上限;n为子域内单元的个数。 通常将多目标问题转化成单目标问题求解用的是线性加权和法,但存在的缺点是无法避免各目标数量级不同时大数量级目标支配优化结果的问题[13]。因此采用折衷规划法得到以柔度最小为目标的多刚体拓扑优化数学模型: (16) 将多个低阶模态频率作为优化目标,采用平均频率法来定义固有频率拓扑优化的目标函数[14],得到以振动频率拓扑优化的数学模型: (17) 式中:Λ(x)为平均频率;λ0、α为给定的参数,用来调整目标函数;m为需要优化的低阶频率的阶次;ωk为第k阶频率的权重系数;λk为第k阶特征频率。 使静态刚度和低阶振动频率最大的同时还需要确保构件质量最小。因此将构件质量最小化作为优化目标函数的拓扑优化数学模型 (18) 式中:f(x)为目标函数,即构件质量;m为单元离散数。 利用带权重系数的折衷规划法与平均频率特征值可得到结构多目标拓扑优化的最终数学模型 s.t β(y)≥β*, l=1,2,…,m;j=1,2,…,n。 (19) 由于静动态模型中的子目标以及综合目标函数中各子目标都对应着一个权重系数,传统的方法是根据有经验的设计者确定各子目标重要性而给出的经验值。当目标函数的子目标增多时,则无法准确客观地分析出各目标的重要性。由此,提出参考决策论中的层次分析法[15],探讨结构拓扑优化中各子目标权重系数。 首先,运用层次分析法构建所要评估问题的决策层次;然后根据配对比较的方法,将各子目标两两比较得出重要程度,列出决策矩阵W=(Wij)n×n,n代表子目标的数目,Wij为第i层决策数与第j层决策数配对比较的重要程度。可以得到 (20) 决策矩阵的特征向量就是各子目标的权重比。给出了初始重要性参考定义如表1所示,用来把决策层次的对比转化为数值的比较。 表1 配对比较矩阵重要性参考定义 在工程实际应用中,采用层次分析法需要确保配对矩阵的一致性,假设一致性不符合要求,需要重新制作配对比较矩阵。根据Saaty等[16-17]提出的配对比较矩阵一致性判断准则,每个配对矩阵都可以导出一致性比值(CR),该值的大小可以来判断矩阵一致性的程度。其中,一致性指标(CI),可表示为 (21) 式中:λmax为求解矩阵的最大特征值;n为子目标数目。一致性比值可表示为: (22) 式中RI为随机产生矩阵的一致性指标,其参考值如表2所示。当RI<0.1时,表明判别矩阵一致性合格,反之重构决策矩阵。最后,根据重要性程度确定各子目标对应的加权系数。 表2 随机一致性指标RI参考值 RB08型工业机器人由底座、腰部、大臂、肘部、小臂和腕关节6大部件组成,共6个关节,基本结构如图2所示。通常情况下,前3个关节用于确定末端执行机构的位置,后3个关节用于确定末端执行机构的姿态[18]。 由于机器人大多采用轻质柔性的材料,则在运动过程中机械臂在较大载荷下,由初始状态依次经历加速、匀速、减速的情况下受力后会有较大的变形和位移变化,产生振动。为更加精确地模拟工业机器人模型的运动状况,有必要在仿真分析中将零部件的柔性变形考虑在内。借助Ansys和Adams软件,建立完整的工业机器人的刚柔耦合动力学仿真模型,选择对研究目标有直接影响的大臂、小臂及底座进行柔性化处理。然后将刚性体与柔性体装配好,形成刚柔耦合模型。 为保证优化时选取各工况下大臂所受载荷为最大,设定施加额定负载8 kg,通过动力学仿真模拟3种不同极限工况,提取响应的载荷谱作为优化的边界条件。在选择提取各工况的载荷时,主要考虑大臂在极限工况时关节3处的载荷。 (1)工况一 关节1旋转,关节2不动,机器人做回转运动,运动范围±170°,最大速度2.09 rad/s,仿真时间2 s,1 000步。 (2)工况二 关节1不动,关节2旋转,机械臂做俯仰运动,运动范围+120°~-85°,最大速度为2.09 rad/s,仿真时间2 s,1 000 步。 (3)工况三 关节1、2同时旋转,机械臂做回转、俯仰运动,回转范围±170°,最大速度2.09 rad/s,俯仰运动范围+120°~-85°,最大速度2.09 rad/s,仿真时间2 s,1 000步。 在运行对应工况时,可以输出得到柔性机械臂上关节点处的载荷曲线,FX、FY和FZ分别对应关节点处中X、Y和Z方向的力,MX、MY和MZ则为其对应方向的力矩,如图3为工况一时大臂关节点处的载荷曲线图。 由图3可知,柔性化的大臂在刚开始的加速过程中载荷振动显著,然后又达到一个稳定值。通过动力学仿真模拟各工况,提取获得大臂局部坐标下的稳定载荷,如表3所示。 表3 各工况下大臂关节处的稳定载荷 本文对工业机器人机械臂结构进行可靠性拓扑优化分析采用的是Hyperworks中的Optistruct模块,基于带惩罚系数的变密度插值法作为材料模型,优化算法选用凸规划法中的移动渐进线法[19]。在拓扑优化前,确定设计区域和非设计区域。设计材料为ZAL201铝合金,其几何参数和材料属性如表4所示。分别用VL、VH、Vd、Vf、VF来指代设计域的长、宽和厚度,体积比、外载荷等随机变量的变异系数。取变异系数Vi=σi/μi=0.1,i=l,h,d,F,f。采用一次二阶矩法计算其对应的可靠性指标,再与许用可靠性指标进行对比评价。求解满足可靠度指标约束的标准正态分布的随机变量,通过式(11)对随机变量进行修正,利用修正后的随机变量对机械臂进行拓扑优化分析。从而将可靠性约束条件转化为等价的确定性约束条件[20]。 表4 大臂的几何参数和材料特性 利用层次分析法确定静态刚度模型中的3个子目标的权重w1、w2、w3,以及综合目标函数中子目标柔度、频率、质量的权值γ1、γ2、γ3。研究的工业机器人考虑了3种工况,则n=3,显然有3个子目标的多目标优化。设3个工况的重要性权重值w1、w2、w3,参考表1对各工况的重要度进行两两比对后建立配对比较矩阵,得到各工况重要性的配对比较矩阵,列出配对比较矩阵W: (23) 求出该矩阵的最大特征值λmax=3.064 9,由n=3可得RI=0.58,根据式(22)求解该矩阵的一致性比CR值为0.055 9<0.1,表明判定该矩阵的一致性满足要求。最大特征值对应的特征向量为α=[0.392 8 0.914 0 0.101 3]T,即为3个工况的重要性权重值。对于频率优化时,取频率阶数k=3,各阶频率的权重系数ωk分别为0.3,0.2,0.2。同样归一化处理后可以确定出综合目标函数中的3个子目标柔度、固有频率、质量的权重值γ1=0.3、γ2=0.5、γ3=0.2。 采用线性加权法处理多目标拓扑优化问题时,对于非凸优化问题来说,存在不能确保得到的Pareto最优解的缺点[21]。针对该问题,利用Optistruct模块中的自定义函数dequation面板,通过线性加权法将折衷规划法和平均频率特征值法所结合的机械臂结构综合目标函数进行自定义设置。依据式(19)的综合目标函数,可将大臂结构的综合目标函数表示如下: (24) 采用层次分析法确定各子目标权重系数,并用折衷规划法对机械臂进行多目标可靠性拓扑优化分析,将最小化综合目标函数(如式(24))作为优化目标,约束为给定许用可靠性指标β*=3.0,且不超过优化设计区域体积分数的0.6,历经多次迭代后收敛。结果如图6~图8所示。 多目标可靠性拓扑优化结果表明,综合目标函数逐渐减小并最终趋于稳定,各工况柔顺度值相比单目标可靠性拓扑优化有所降低,而前三阶振动频率相比单目标可靠性拓扑优化有一定增加且都没有产生交替现象。尽管刚度和固有振动频率之间存在不同属性,但从整体变化趋势上来看比较平稳,并没有受到影响。如图9所示为大臂优化后的材料密度分布云图,浅色部分是需要保留的材料,深色部分是在实际工作中不受干扰的部分,在设计区域中可以考虑去除,对于单元密度处在0和1之间的灰白色部分,材料是否去留要看工程实际需要,从而达到材料的高效率利用,实现轻量化设计。 最后,通过OSSmooth的单元密度阈值,将大臂的多目标可靠性拓扑结果导入到Creo1.0中,得到如图10所示大臂结构模型。对于重新设计的大臂进行优化,如表5所示得到优化前后的分析结果。可以得出各工况对应的应力和变形均有一定程度减小,各阶振动频率值都有显著的提高,机械臂总质量为15.25 kg,优化后相对初始质量减少10.2%。 表5 优化前后大臂的性能对比 本文建立了工业机器人刚柔耦合动力学模型,将可靠性方法和拓扑优化方法相结合,在充分考虑各随机不确定性因素的情况下,基于一次二阶矩法得到可靠度指标,然后将可靠度指标作为约束条件,建立了静态刚度、前三阶振动频率和构件质量的综合目标函数,在保证了工业机器人具有良好的静动态性能的条件下,实现了多目标的可靠性拓扑优化,找到了经济性与安全性的最佳结合点,确保获得性能更优的机器人优化设计方案。 通过可靠性理论将随机变量转化为确定性设计参数,然后对机器人进行确定性的拓扑优化设计。避免了拓扑优化过程中复杂的可靠性分析,从根本上提高了多目标可靠性拓扑优化的计算效率。 本文基于变密度插值法的优化准则提出了折中规划法对子目标进行归一化处理,通过层次分析法确定工业机器人子目标权重系数,在一定程度上减少了设计者的主观因素造成权重比的误差,完善了多目标可靠性拓扑优化模型。通过对比可知,优化后在满足可靠性要求下工业机器人在刚度、固有频率和质量上均有所改进,充分证明了本文所提方法的可行性和适用性。 针对实际工业机器人的结构设计阶段往往会涉及非线性材料属性、多物理耦合场等问题。在工业机器人结构设计过程中,综合考虑材料最佳性能参数、结构-热-电耦合等相关问题,进行工业机器人结构可靠性拓扑优化是今后研究的方向之一。
2.3 动态固有频率拓扑优化模型
2.4 构件质量拓扑优化模型
2.5 多目标可靠性拓扑优化的综合模型
3 各子目标权重系数的确定方法
4 机器人刚柔耦合模型的分析
5 多目标的臂部可靠性拓扑优化设计

5.1 确定各子目标权重系数

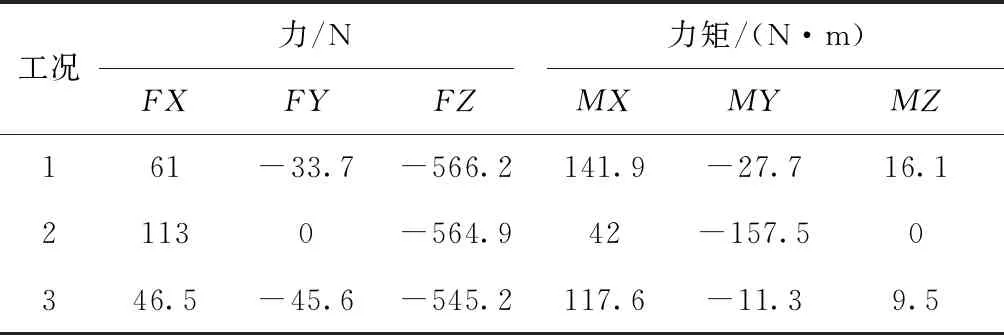
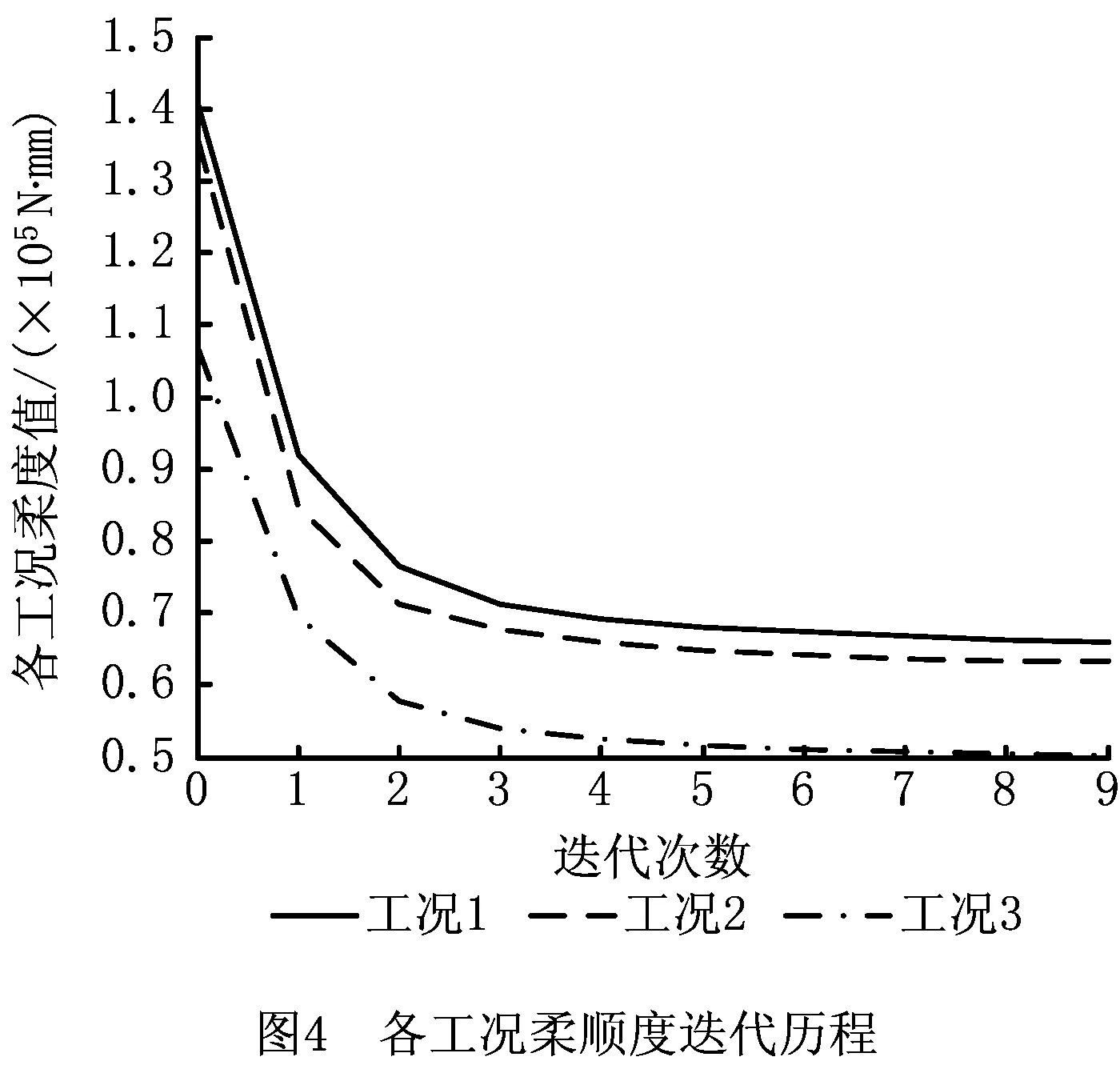
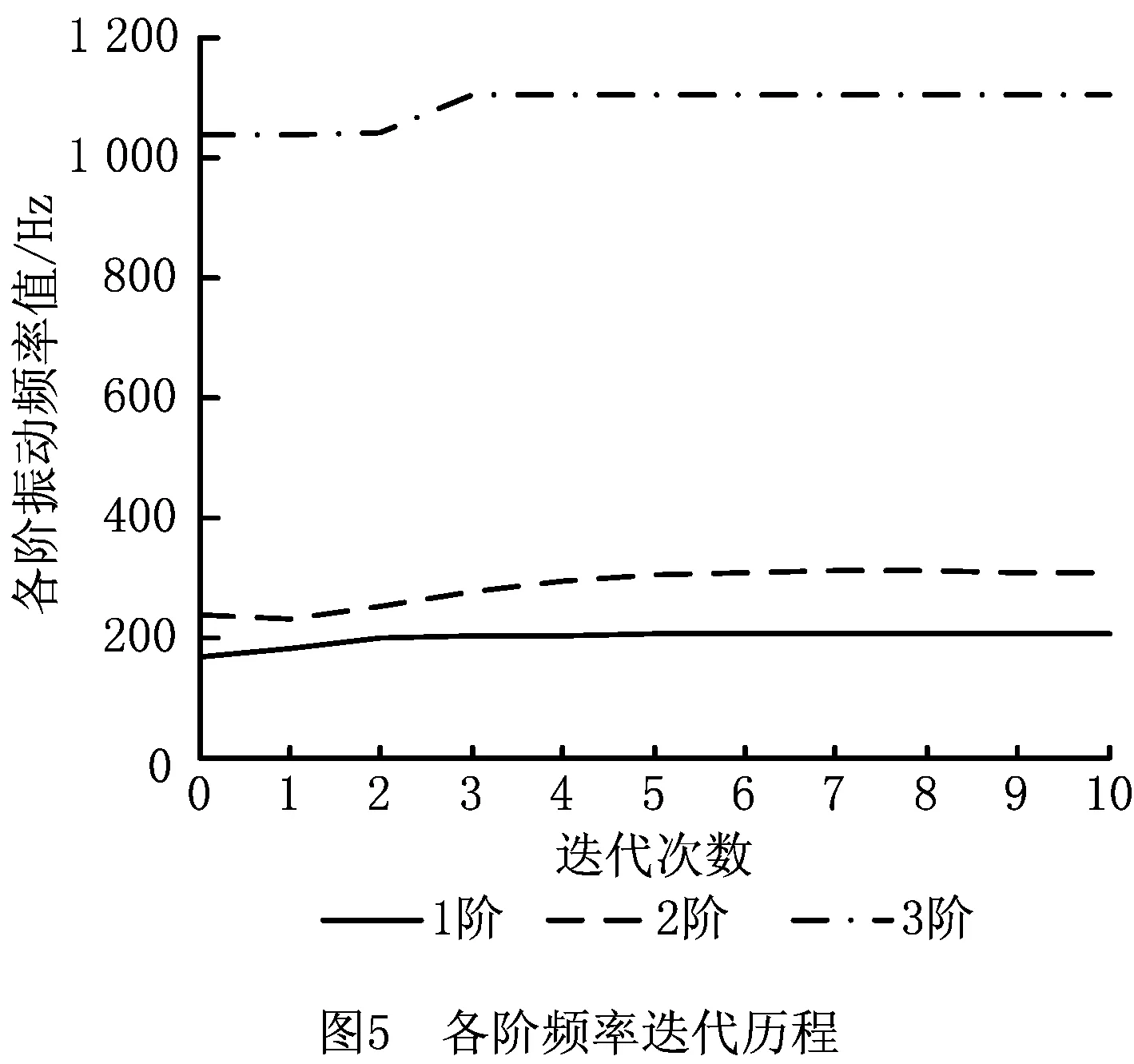
5.2 单目标可靠性拓扑优化分析

5.3 基于层次分析法的多目标可靠性拓扑优化

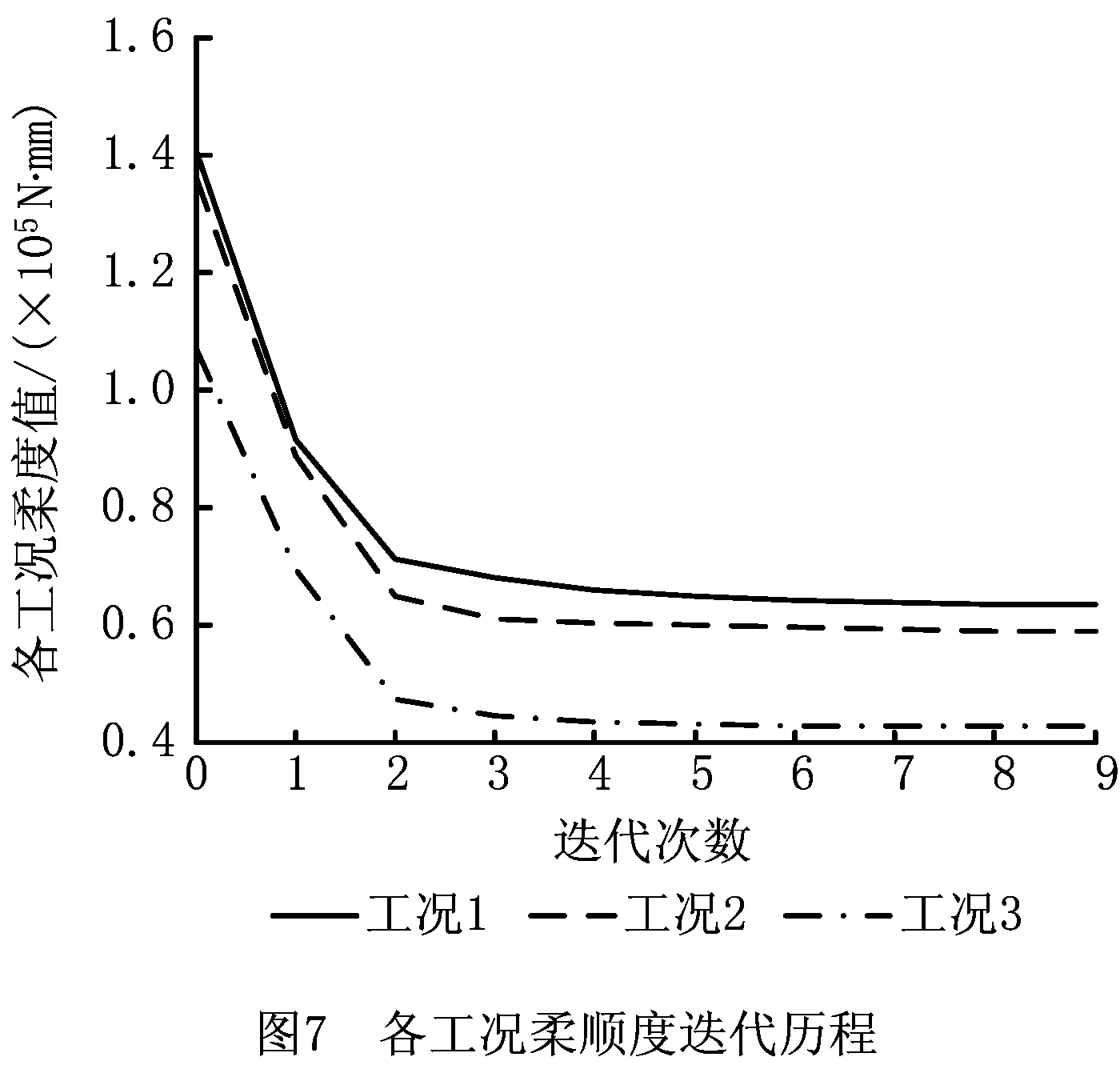
5.4 多目标可靠性拓扑优化结果及分析



6 结束语

