基于Deodatis法的输电塔风振响应时域分析
宋智丰, 邹孔庆, 张 延
(1.合肥工业大学 土木与水利工程学院,安徽 合肥 230009; 2.中铁四局集团钢结构建筑有限公司,安徽 合肥 230022; 3.安徽水利水电职业技术学院,安徽 合肥 231603)
输电塔是一种工程数量较多、分布较广的重要高耸结构,为重要的电力设施,输电塔的破坏可能直接导致供电系统的破坏,影响人们正常的生活秩序及生产建设。影响输电塔安全的最重要因素就是风荷载的作用,由于风具有随机性和复杂性,导致结构的风致振动问题尚未在理论上得到较完善的解答[1]。在设计输电塔时,风荷载通常按照静力风考虑,忽视脉动风产生的影响,但实际上输电塔是处于随机脉动风场环境中,会产生随机振动,主要由平均风压和脉动风压共同作用,前者是静力作用,后者是脉动风作用。本文着重研究脉动风作用下的抖振响应。
在随机风荷载作用下的结构响应分析方法主要有频域法[2]和时域法[3]。其中,频域分析方法简单,但需要考虑一定量的模态数,得到的结果响应值为数字特征,并且只适用于线性分析;而时域法通常对结构进行单元离散后再进行时程分析,进而得到各种响应的时程曲线,计算结果较为清晰、简单。
本文以沿海某地实际工程220 kV典型输电塔为研究对象,利用ANSYS建立输电塔三维结构有限元模型,并分析该模型的动力特性;利用Matlab编程实现基于Deodatis的谐波合成法(weighted amplitude wave superposition,WAWS)模拟输电塔的随机脉动风场,并进行检验;在各种来流风攻角作用下对输电塔进行风振响应时域分析。
1 输电塔模型与模态分析
利用有限元分析软件ANSYS建立输电塔的三维结构有限元模型,其中忽略主塔、基础、地基三者的相互影响,模型主要由主杆件(弦杆、主腹杆)和次弦杆(横隔杆、次腹杆)组成,主杆件采用BEAM188单元,次弦杆采用LINK8单元,整个模型共有362个节点、480个单元,建立的输电塔有限元模型如图1所示。边界条件采取底部固结,主杆件采用刚接,次杆件与主杆件采用铰接。
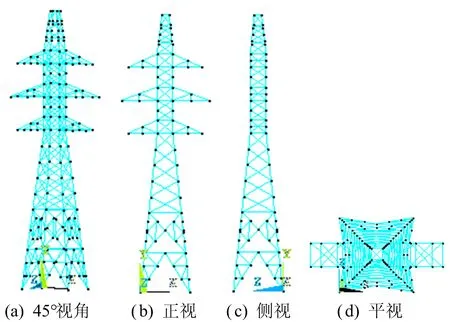
图1 有限元模型
模态分析可验证结构模型的正确性与结构振动特征,得到的固有振型和频率作为动力分析的基础参数。本文采用子空间迭代法(Subspace法)分析输电塔有限元模型的固有频率与振型,频率(f)结果见表1所列。由表1可知,输电塔的基本周期约为0.150 s,周期较长的主要集中于前3阶。前3阶振型如图2所示,第1阶振型为侧向弯曲,第2阶为纵向弯曲,第3阶为底部系杆纵向弯曲。
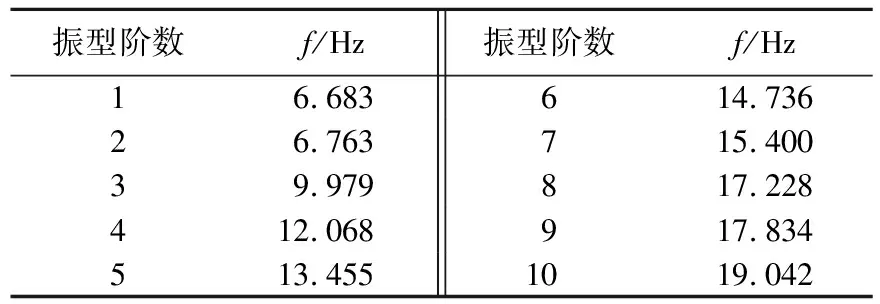
表1 输电塔模型的模态频率
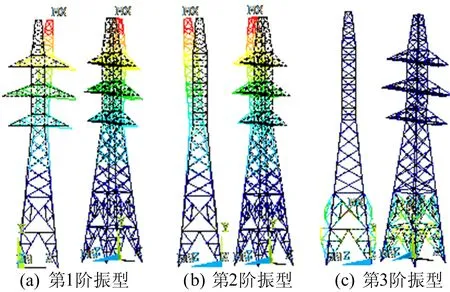
图2 输电塔振型
2 脉动风场的数值模拟
2.1 谐波合成法模拟理论
本文基于George Deodatis 提出的WAWS,并采用规范规定Deodatis谱[5]模拟该输电塔处的空间脉动风速,沿塔高方向上设置n条风力施加点,共形成n维零均值平稳高斯随机过程向量,即
f(t)=(f1(t),f2(t),…,fn(t))T
(1)
其中,fj(t)(j=1,2,…,n)为第j点处数值模拟脉动风速随机过程。fj(t)计算公式[6-7]为:
cos[ωmlt-θjm(ωml)+Φml],
ωml=(l-1)Δω-(m/n)Δω,
(2)
其中,N为较大正整数,假设N趋于无穷大;ωml为采样频率;Δω为频率增量,Δω=ωup(ωup为截止圆频率);Hjm(ωml)为下三角矩阵H(ω)的正元素;θjm(ωml)为Hjm(ω)的复角;Φml为均匀分布在[0, 2π]区间内的随机相位。
互功率谱密度矩阵为S0(ω),当ω>ωup时,S0(ω)=0;下三角矩阵H(ω)为S0(ω)的Cholesky分解,S0(ω)=H(ω)HT*(ω)。
(3)
周期T0=3×2π/Δω;为避免产生频率混淆问题,时间步长Δt需要满足Δt≤2ω/(2ωup)。
由于输电塔沿塔高度上自然风的风速正交谱很弱,可忽略其影响,则沿塔高方向上各点的互功率谱表达式[8]为:
j,m=1,2,…,n;j≠m
(4)
其中,Δjm为j、m点间的竖向距离;Coh(Δjm,ω)为相干函数。
为提高计算效率,数值模拟采用快速傅里叶变换(fast Fourier transform,FFT)技术,已知功率谱S0(ω),选择适当N、ωup、Δt3个参数进行编程可得到各点处随机过程样本。
2.2 脉动风速时程模拟与检验
研究不同风攻角作用下输电塔的抖振响应时域,需要模拟出不同风攻角下的脉动风速时程曲线,按照上述脉动风速谐波合成法,采用Matlab编制相应脉动风速时程模拟程序。该输电塔场地类型为A类,风场数值模拟的目标谱为Kaimal谱,相干函数为Davenport,风速场模拟主要参数见表2所列。
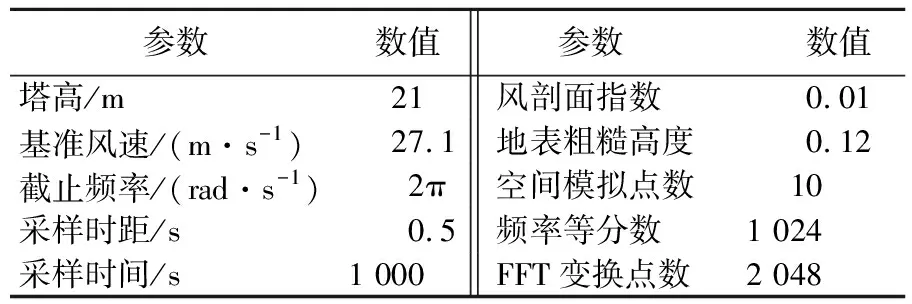
表2 风速场模拟主要参数
表2中,截止频率为圆频率,它与结构固有频率没有关系,仅对脉动风速时程模拟有一定的影响,是模拟脉动风随机过程的关键控制参数,其大小通常由功率谱密度矩阵中各项与ω的函数关系确定。
各风攻角(B)来流方向如图3所示,分别取0°、15°、30°、45°、60°、75°、90°共7种不同的风攻角作为分析对象。每种来流方向沿高度方向上均模拟了10条脉动风速时程。以风攻角0°为例,模拟得到塔顶处的脉动风速时程曲线如图4所示,对模拟功率谱函数及相关函数与目标函数进行验证,如图5所示。
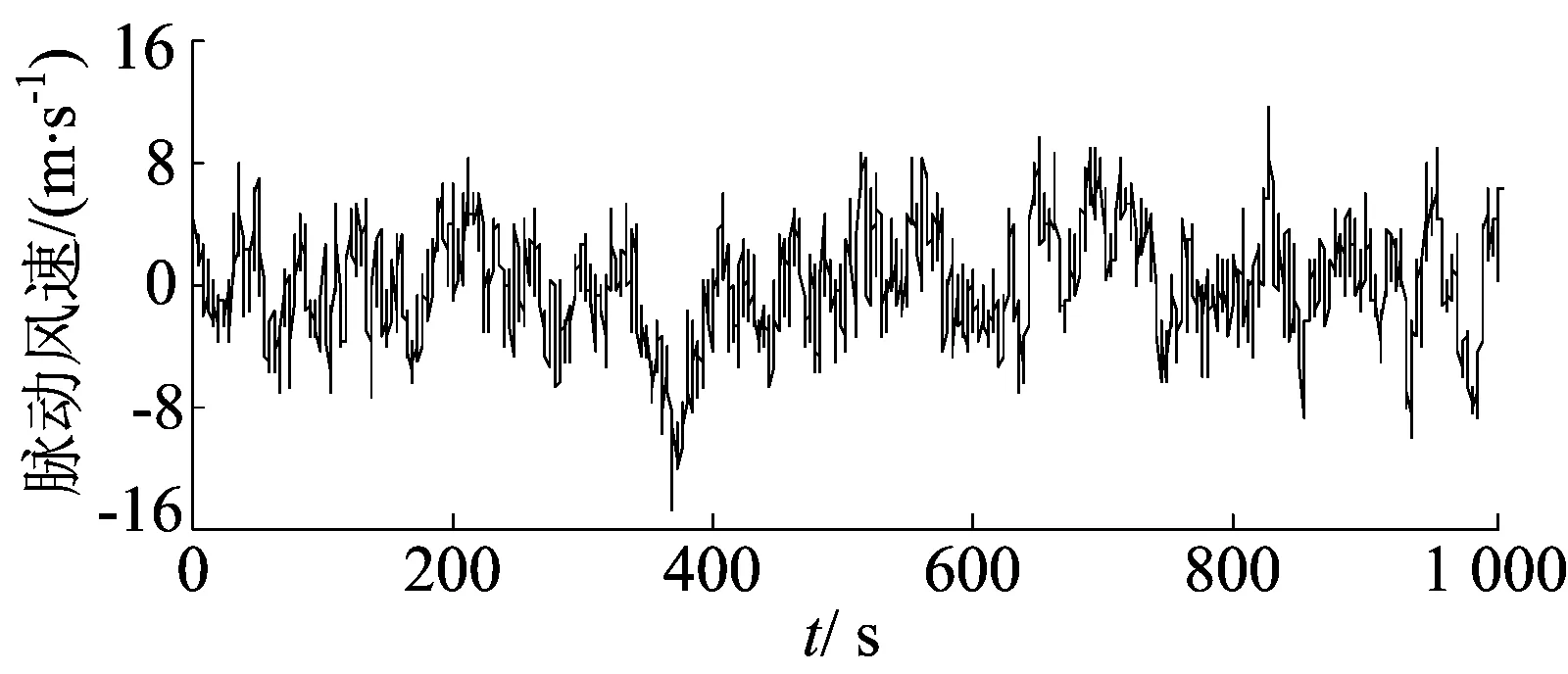
图4 主塔顶脉动风速时程曲线
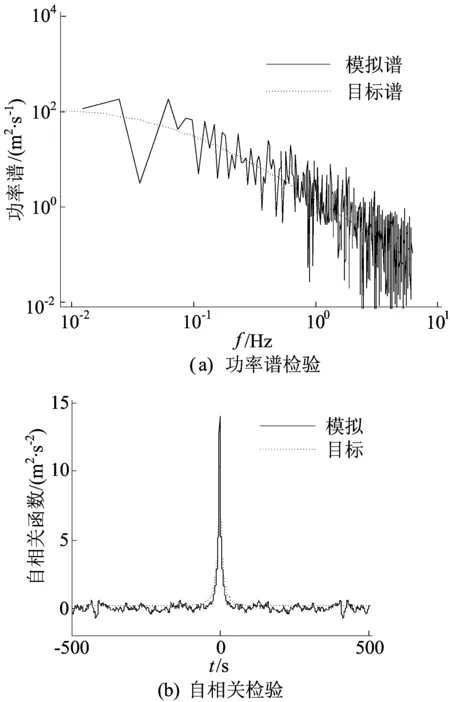
图5 主塔顶脉动风速功率谱、自相关与目标函数检验
从图5可以看出,模拟结果与目标的吻合度较好,说明模拟结果与程序是可靠、有效的。
3 输电塔结构的响应分析
3.1 风荷载转换
得到输电塔处脉动风速时程后,计算各点处的脉动风荷载,计算公式为:
(5)
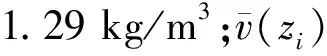
输电塔的迎风面积见表3所列。

表3 输电塔的迎风面积
此风荷载转换过程需在Matlab软件中实现,在考虑节点等效迎风面积因素下,将模拟数据转换为脉动风荷载时程曲线。
3.2 结构抖振响应结果
利用ANSYS中的APDL进行二次开发实现循环加载。计算中分别考虑7种不同风攻角的作用,根据近似Rayleigh阻尼模型公式,利用模态分析结果计算得到输电塔的阻尼系数α=0.067 2,β=0.125。这里仅以0°、45°风攻角为例,计算时间取1 000 s。采用Newmark逐步积分方法对该结构进行抖振时域分析,并结合基于模态贡献度系数计算结构最优时间步长法[10]求得步长为0.005 s,得到塔顶处的抖振时程响应如图6所示。
对不同风攻角作用下的不同高度处进行抖振响应均方根值(root mean square,RMS)分析,结果如图7所示。
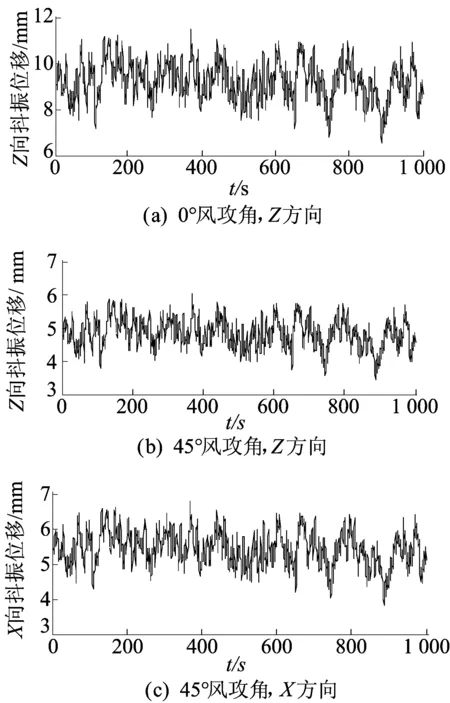
图6 0°、45°风攻角下塔顶点位移响应时程
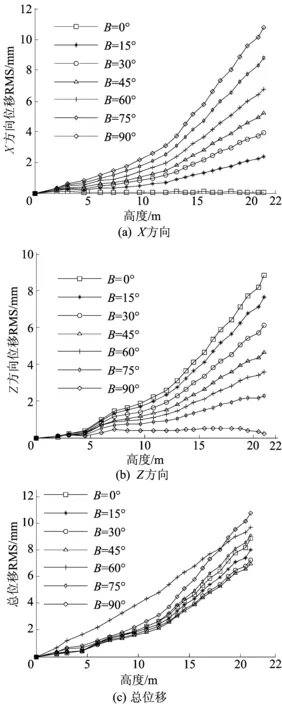
图7 不同风攻角下沿X、Z方向位移及总位移的RMS
从图7a、图7b可以看出,随着风攻角不断增大,输电塔X方向抖振响应RMS逐渐增大,而Z方向RMS逐渐减小;X、Z方向上的RMS变化幅度较大区段均位于14~21 m高度内。从图7c可以看出,除了风攻角60°、90°外,总位移RMS变化不大,但在风攻角60°作用下的同一高度处,抖振响应RMS与其他风攻角作用下的结果相差较大,这主要是由于输电塔结构本身在X、Z轴上具有不同的抗弯能力,风攻角60°作用下接近输电塔界面弱中性轴。上述结果可为合理设计输电塔结构提供参考。
4 结 论
本文针对某地的典型输电塔结构,编程实现了输电塔处脉动风速数值模拟,并研究了结构在不同风攻角作用下的抖振响应时域,得到如下结论:
(1) 采用改进的谐波合成法及FFT技术,实现了输电塔处脉动风场的数值模拟,并对模拟的效果进行了检验,模拟结果与目标的吻合度较好,说明模拟方法与程序是可靠、有效的。
(2) 输电塔结构对不同风攻角作用下抖振响应的敏感程度是不同的,主要体现在主迎风面方向的抖振响应较为显著。同一风攻角作用下,不同高度内响应程度也是不同的,靠近塔顶段(占塔高的1/4)的敏感程度较强。
(3) 输电塔在风攻角为60°时,沿塔高方向上产生的抖振响应总位移均方根值较大,主要是由结构本身的布置形式导致的,此方向是抗风设计时应考虑的不利方向。本文研究结果可为同类输电塔的设计提供参考,为异类型输电塔结构抗风抖振响应分析提供一定思路。

