具有双疾病的随机SIRS传染病模型的灭绝性与持久性分析
, ,
(广西师范大学数学与统计学院,广西桂林541006)
长期以来, 传染病的流行给人类健康造成巨大伤害, 人们一直很重视传染病的预防和控制, 因为它一旦失控, 轻则危及人的生命, 重则影响种族延续和国家的存亡。传染病的防控不仅是公共卫生问题, 更是公共安全问题, 因此,传染病的研究吸引了大量学者,运用数学建模建立了很多传染病模型[1-5], 研究其传播规律, 通过人为干预来切断疾病的传播途径, 从而达到控制疾病传播的目的。但是大多数学者在建立数学模型时只考虑了一种疾病的影响, 而在实际生活中, 同一个群体中可能同时存在2种疾病, 因此也有部分学者研究了双疾病传染病模型的动力学行为[6-8], 例如Meng等[7]研究了一类具有双疾病的非线性随机SIS传染病模型:
(1)

(2)
该文献主要考虑的是第一种疾病是关于染病者的饱和发生率, 第二种疾病是关于易感者的饱和发生率, 应用相应的随机微分方程的知识得到了环境干预下疾病灭绝与持久的条件以及白噪声强度对疾病所产生的影响。
由于在实际生活中, 当染病者数量增加时, 传染率趋于饱和状态, 疾病的流行在一定程度上会受到心理因素的影响[12], 当染病者的数量增加, 人们开始重视, 从而通过采取一些措施(如隔离、媒体宣传等)来控制接触率, 进而降低传染率。因此, 为了更好地描述心理因素对疾病的影响, 对第一种疾病和第二种疾病都采用关于染病者的饱和发生率, 根据相关的染病机制, 建立如下的SIRS传染病模型:
(3)
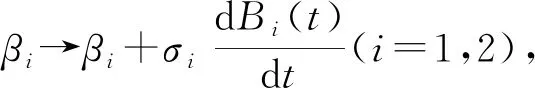
(4)
1 全局正解的存在唯一性


定义正不变集为
对于模型(4), 首先考虑其正解的全局存在唯一性。


τη=inf{t∈[0,τe):S(t)≤η或I1(t)≤η或I2(t)≤η或R(t)≤η}。
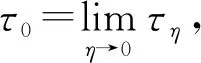

其中
因此
(5)
对式(5)两边同时从0到τη∧T积分, 并取期望, 则有
EV(S(t),I1(t),I2(t),R(t))≤V(S(0),I1(0),I2(0),R(0))+KT。
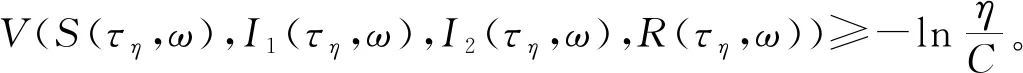
因此

其中χΩ是Ωη的示性函数。令η→0, 则有
∞>V(S(0),I1(0),I2(0),R(0))+KT=∞,
矛盾, 所以τ0=∞ a.s., 即模型(4)存在唯一的全局正解。证毕。
2 疾病的灭绝与持久
2.1 疾病的灭绝
本节主要讨论在白噪声干预下模型(4)中两种疾病都灭绝的条件, 定义随机基本再生数为

(6)
或

(7)
则SDE模型(4)中的两种疾病都灭绝。
证明根据It公式, 有:
(8)
对式(8)两边积分, 有:

(9)
其中
(10)

此时
(11)
对式(11)两边同时除以t,得:
(12)
因为Mi(t)(i=1,2)是一个局部鞅, 根据鞅的强大数定理[14], 有:
对式(12)两边取上确界再取极限得:


(13)
根据式(9), 有
(14)
因此

注此定理说明白噪声在一定强度下, 两种疾病都灭绝, 并且由条件(6)知, 大的白噪声强度会抑制疾病的爆发。
2.2 疾病的持久性
研究流行病动力学行为, 除了关心疾病在什么情况下灭绝, 也关心疾病在什么情况下流行, 并长期存在。因此, 本节将讨论两种疾病在时间均值意义下的持久性。
定理3令(S(t),I1(t),I2(t),R(t))是模型(4)关于初值(S(0),I1(0),I2(0),R(0))∈Γ的解, 则有:





其中
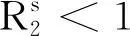

(15)
因此,
(16)
对a1lnI1(t)+I1(t)运用It公式, 有:
(17)
对式(17)从0到t积分, 并且两边同时除以t, 再根据式(16)有:

(18)
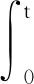
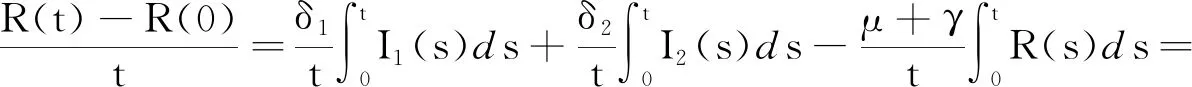
所以
(19)
根据式(18)、(19)有:

(20)
根据式(20)有:

当0≤I1(t)≤1时, 有:

(21)
当I1(t)≥1时, 有:

(22)


(23)
对a2lnI2(t)+I2(t)运用It公式, 有:
(24)
对式(24)从0到t积分, 并且两边同时除以t, 再根据式(19)、(23)有:



(25)
根据式(25), 当0≤I2(t)≤1时, 有:

(26)
当I2(t)≥1时, 有:

(27)

③根据式(15)、(19)知:
(28)
定义如下Lyapunov函数
对上式两边积分, 根据式(28), 则有:
所以
(29)
对式(29)取下确界再取极限, 令t→∞, 则
定理得证。证毕。
3 数值模拟
在本节中, 为了验证所得结论的正确性, 利用Milstein方法[16-17]和Matlab 软件数值模拟不同白噪声强度对疾病持久性和灭绝性的影响。将模型(4)离散化可得到如下形式
选择初值(S(0),I1(0),I2(0),R(0))=(10,7,5,5), 参数取值如下:Λ=4,μ=0.25,β1=0.7,β2=0.8,a1=10,a2=10,α1=0.4,α2=0.3,δ1=0.1,δ2=0.2,γ=0.3。

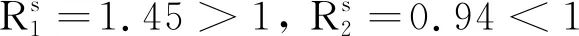



图1 随机系统(4)关于初值(S(0),I1(0),I2(0),R(0))=(10,7,5,5)的路径Fig.1 The path of S(t),I1(t),I2(t) and R(t) for the stochastic model (4) with initial values (S(0),I1(0),I2(0),R(0))=(10,7,5,5)
4 结论