某泳池上方大跨钢-混凝土组合楼盖计算与分析

张鸿雁，刘 坚

（1、中交第四航务工程勘察设计院有限公司 广州510230；2、广州大学 广州510006）

0 引言

随着生活水平的不断提高，人们对运动、健康等日益重视，对游泳馆、健身房、体育馆等运动场所需求不断加大。此类运动场馆大多需要大空间以满足使用要求。此时，轻质、高强的钢-混凝土组合楼盖、预应力技术以及新型结构体系有了充分的使用空间。其中钢-混凝土组合楼盖因技术成熟、施工方便，得到了广泛的应用。

工程设计中，混凝土楼板多采用不考虑支撑梁的刚度和竖向位移、边界简化为理想的铰接和固接的模型，按弹性理论、考虑塑性内力重分布的方法或极限分析方法计算［1］。复杂的混凝土楼板多采用程序默认的梁板中线对齐的弹性板细分模型计算复核，此种模型可以一定程度上考虑梁板的协同作用。实际上，梁和楼板在中线不对齐的状态下协同工作，共同受力和变形，二者相互影响［2-4］。次梁作为楼板的弹性支座，其刚度变化与楼板的内力及变形有着直接联系［2］。

钢-混凝土组合楼盖中，钢梁与混凝土多为铰接，简支钢梁刚度较小，对楼板的弹性支座效应亦较小，楼板的变形接近无次梁楼盖，楼板的分析应按整跨（四周主梁跨度）考虑。另外，大跨钢-混凝土组合楼盖竖向刚度较弱，其舒适度问题不容忽视。

为进一步了解钢-混凝土组合楼盖结构的实际受力和变形情况，采用通用建筑结构有限元软件STRAT对某泳池上方20.70 m×26.25 m 的大跨钢-混凝土组合楼盖进行了考虑梁板中线相对关系的精细化建模计算，并与常规查表法和梁板中线对齐的有限元楼板计算结果进行对比分析。

1 工程概况

本建筑长36.15 m，宽35.8 m，主体结构为3 层混凝土框架，首层设置商铺、埋地式室内游泳池和配套机房，层高4.1 m，2层和3层做中小学生辅导培训机构办公室，层高分别为3.3 m。根据经营方要求，首层泳池中间不设柱，故泳池上方在2 层、3 层及屋面均存在20.70 m×26.25 m 的大跨楼板。综合考虑楼层净高、施工便捷性和可靠性后，确定采用钢-混凝土组合楼盖。

泳池四周柱子截面主要为500 mm×600 mm、500 mm×500 mm、400 mm×400 mm，混凝土梁截面主要为300 mm×600 mm、400 mm×1 000 mm，钢梁截面为 H750×300×12×20，2、3 层板厚均为110 mm，屋面板厚为120 mm，均采用钢筋桁架楼承板。各层结构平面图如图1所示。

2 分析模型

钢梁的钢材等级为Q235B，混凝土强度等级为C30，钢筋强度等级为HRB400。

楼面荷载：恒载2 kN/m2；考虑隔墙预留后，活载取5 kN/m2。上人屋面荷载：恒载5 kN/m2；活载取2 kN/m2。本文仅考虑竖向荷载作用下钢-混凝土组合楼盖的受力和变形，未考虑水平风荷载和地震作用。

图1 各层结构平面图Fig.1 Structure Plan of Each Floor

采用通用建筑结构有限元软件STRAT进行分析，梁和柱采用梁单元，楼板采用壳单元，计算中考虑混凝土框架梁柱端刚域、梁与壳单元变形协调、梁沿高度方向设置偏心模拟梁板相对关系［5-7］、梁扭矩不折减、考虑施工模拟。壳单元按最大控制长度0.35 m 细分，梁刚度不放大。为更准确地模拟周边结构对大跨楼盖的刚度贡献，采用整体建模，柱跨及楼层数目不做删减。楼梯采用滑动楼梯，未建入模型中［8］。梁板关系示意图如图2所示。

图2 梁板关系示意图Fig.2 Diagram of Beam-slab RelationShip

3 楼盖计算结果分析

限于篇幅，本节分析的钢-混凝土组合楼盖仅为首层泳池正上方的2层楼盖。

3.1 弹性挠度计算结果分析

泳池四周为柱距约6 m 的现浇混凝土框架，上方大跨钢-混凝土组合楼盖变形接近四周混凝土框架围绕而成的大跨楼板，整体呈下凹的“盆地”形状，如图3所示。中间钢梁作为大跨楼板的竖向“肋板”，有效地减小了楼板的变形和内力。

若按工程中常用的查表法，则此处楼板会按跨度2.2 m 的连续跨楼板设计，主受力方向钢梁认为是无竖向位移的固结支座，每区格板跨中挠度很小，而这是明显偏离实际认知的。在设计大跨楼板时，此种方法是不准确且不安全的。

若采用梁板单元中线对齐的壳元模型计算，楼板整体变形趋势类似图3。但即使按《高层民用建筑钢结构技术规程：JGJ 99-2015》［9］考虑楼板对钢梁的刚度增大作用后，楼板的挠度仍大于梁板顶平模型。恒载+活载工况组合下，梁板中线相对偏移模型中板最大挠度为32.9 mm，梁板中线对齐、梁刚度放大1.5 倍的模型中板最大挠度为70.2 mm，二者差异明显。钢梁对楼板竖向刚度的增大作用明显，梁板中线对齐模型会严重低估钢梁的这种增大作用。在需要准确计算楼板竖向变形和竖向自振频率时，应采用梁板中线相对偏移的模型［10］。

图3 钢-混凝土组合楼盖挠度Fig.3 Deflection of Steel-concrete Composite Floor

3.2 楼板内力计算结果分析

图4为此区域楼板分块示意，沿X向共分12块小板（图4 中LB*），每个柱跨间的三块小板合称一个大板（图4中DB*），1～3表示大板的主梁支座位置，4～9表示小板的跨中位置，10、11表示DB1、DB2的非主受力向支座。

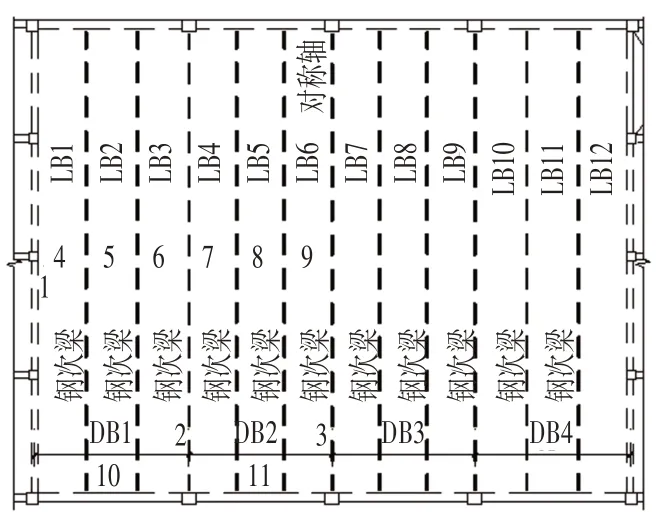
图4 楼板分块示意图Fig.4 Schematic Diagram of Slab Block

梁板中线相对偏移模型的楼板弯矩Mx和My云图如图5所示，梁板中线对齐模型的楼板弯矩Mx和My云图如图6 所示。由图5、图6 可知板内力近似左右对称，对称轴为最中间的钢主梁位置。为了简化篇幅，表1仅列出对称轴左侧1～11点的内力。

对比图5、图6可知：

图5 梁板中线相对偏移模型的楼板弯矩云图Fig.5 Cloud Chart of Slab Bending Moment Based on the Relative Offset Model of Beam Slab Center Line

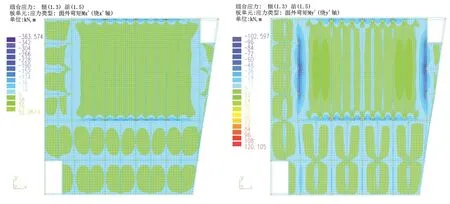
图6 梁板中线对齐模型的楼板弯矩云图Fig.6 Cloud Chart of Slab Bending Moment of Beam Slab Center Line Alignment Model

⑴ 两种模型的Mx分布总体趋势相同，数值上前者比后者小很多。上方混凝土框架边梁因受力及搭接钢梁需要，截面较大，对楼板有较大的约束作用，板面出现支座负弯矩，若仅按查表法的简支边构造配筋，不满足强度需求，需按计算配置支座筋。整个2层混凝土楼盖弯矩出现明显的“大小跨”效应（见图7），大跨楼板下方的8.15 m跨板支座附近很长范围内出现负弯矩，而此处恰是查表法中单向板的短边支座，配筋很小，实际配筋应考虑楼板的“大小跨”效应，按需加大板面支座筋长度，此工程支座筋需向下方8.15 m 板跨内延伸4 m以上。

图7 板弯矩Mx切面图Fig.7 Section of Slab Bending Moment Mx

⑵ 两种模型的My分布趋势不同的地方：考虑梁板中线相对关系后，中间3 道与柱相连的钢主梁上方楼板出现明显的负弯矩，且越靠近柱的位置负弯矩越大；梁板中线对齐时，大跨楼板最中间一道与柱相连钢主梁及两侧相邻钢次梁上方出现很小的负弯矩，而另外两道与柱相连、相对刚度比钢次梁大的钢主梁上方楼板却未出现负弯矩，无法正确反映中间钢梁对楼板的弹性支座作用。

⑶ 两种模型的My分布趋势相同的地方：二者均在左侧的LB1和右侧的LB12整跨内出现负弯矩，此处楼板支座负筋配置时应注意加长，不可仅按LB1、LB12短跨的1/4 配置，此工程需至少按DB1 和DB4 板跨的1/3以上设置。整个组合楼板的左右侧为跨度较小的板，My亦存在“大小跨”效应，尤其右侧跨度小的楼板，会出现全跨负弯矩，此处实配支座筋伸至框架边梁。

⑷ 两种模型的楼板轴力分布有明显差异：考虑梁板中线相对关系后，2 层楼板内出现较大的拉力和压力，一般是竖向刚度大的地方出现拉力，反之出现压力；梁板中线对齐时，2层楼板内大部分为相对较小的拉力，很少区域出现压力。典型位置楼板轴力如表1所示。

3.3 楼板配筋计算结果分析

楼板配筋近似左右对称，对称轴为最中间的钢主梁位置。为了简化篇幅，表2仅列出对称轴左侧LB1～LB6的小板配筋。每块小板的配筋计算点如图8所示。

对比表2中各种计算方法的配筋结果可知：

⑴ 查表法仅为构造配筋，两种有限元模型不同程度反映了梁、柱对楼板的弹性约束作用，与查表法的结果差别明显，查表法无法体现楼板的整体受力，楼板配筋存在安全问题；

⑵ 梁板中线相对偏移时，板跨中Y向

存在较大压力，计算结果显示板底Y向无需配筋；梁板中线对齐时，板跨中Y向存在拉力，板底Y向需配筋，且其值大于构造值；

表1 1～11点的楼板轴力Tab.1 Axial Force of Slab at Points 1-11 （kN/m）

表2 LB1～LB6板配筋结果Tab.2 Reinforcement Results of LB1～LB6 (mm2/m)

图8 板配筋计算点Fig.8 Reinforcement Site of Slab

⑶ 两种有限元模型均显示，在框架柱附近，楼板支座筋长度需要比其他区域的大很多；

⑷ 梁板中线对齐时，X向和Y向底筋均比梁板中线相对偏移模型的结果大，整个钢-混凝土组合楼板的左右侧混凝土框架梁处楼板支座配筋也比梁板中线相对偏移模型的结果大，但中间3 道钢主梁上方的支座筋明显偏小很多。

3.4 楼板舒适度计算结果分析

3.4.1 计算模型

分析模型取全部2 层楼面，同时保留与楼盖相连的上下层柱［11］，以便考虑相邻构件的影响（见图9）。下层柱底嵌固，上层柱顶约束水平向位移，对2层梁侧面约束水平向位移、转动不约束。根据前文所述，梁板中线相对偏移关系对楼盖竖向刚度影响很大，为保证楼板的特性不受影响，采用梁板中线相对偏移的有限元模型计算楼盖自振频率和加速度。

考虑装修面层和下部吊顶后，楼板恒荷载取1.5 kN/m2；目前隔墙位置不固定，《建筑结构结构荷载规范：GB 50009-2012》［12］规定活荷载至少按 1 kN/m2预留，取下限值1 kN/m2，另外根据《建筑楼盖结构振动舒适度技术标准：JG/T 441-2019》［13］，办公楼有效活载取0.5 kN/m2，综合后，活荷载取1.5 kN/m2。

混凝土材料弹性模量提高1.35倍［13］，钢材弹性模量不放大，阻尼比取0.03。板单元按0.35 m 划分，这样既可以保证每个次梁之间划分不少于4 个单元［11］，也可与行走激励荷载的步距协调，方便加载。

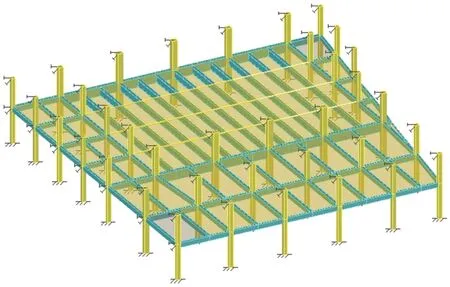
图9 楼盖模型Fig.9 Floor Model

3.4.2 组合楼盖自振频率分析

2层楼盖结构的前5阶振型表现为泳池上方20.7 m×26.25 m范围的大跨钢-混凝土组合楼盖竖向振动，从第6振型开始其他部分楼板参与振动。前5阶振型的频率分别为4.29 Hz、4.59 Hz、5.22 Hz、5.95 Hz、7.81 Hz。

由此可知，钢-混凝土组合楼盖的竖向自振频率均大于3 Hz，满足规范的频率限值要求［9］。图10为楼盖前5 阶振型情况，可以发现大跨钢-混凝土组合楼盖是整个2 层楼盖中最弱的地方，需进一步做楼板加速度响应分析。

3.4.3 组合楼盖加速度响应分析［13］

图10 前5阶振型图Fig.10 Top 5 Mode Shapes

本建筑使用功能主要为中小学生辅导培训机构办公室，属于以行走激励为主的楼盖结构，可按单人行走激励计算楼盖的振动响应。组合楼盖的前几阶自振频率很接近，计算峰值加速度时，考虑楼盖的前三阶模态的影响。

行走激励荷载按下式计算：

式中：Pp=0.7 kN；γi、φi按规范取值，由于f1/3=4.29/3=1.43 Hz＜1.60 Hz，所以取=1.60 Hz。

根据前面计算得到的楼盖竖向模态，确定楼板振动的不利区域，选取最不利的行走路径施加行走激励。在给定激励下，取行走路径上的最不利节点加速度响应（见图11），其最大值为22 mm/s2，小于规范中的办公室峰值加速度限值50 mm/s2，舒适度满足要求。

图11 最不利节点加速度响应Fig.11 Acceleration Response of the Most Unfavorable Node

4 结论

本文通过对某泳池上方大跨钢-混凝土组合楼盖的计算与分析，得出以下主要结论：

⑴ 大跨钢-混凝土组合楼盖中，楼板的变形接近无次梁楼盖，楼板的分析应按整跨（四周主梁跨度）大板考虑。

⑵ 梁板中线相对关系对板的内力及变形影响很大，当需对大跨楼盖结构中的楼板进行详细分析时，应采用梁板中线相对偏移的模型。

⑶ 大跨组合楼盖与相邻小跨楼盖间存在明显的“大小跨”效应，尤其当小跨楼盖跨度较小时，甚至会全跨出现负弯矩，支座筋伸入小跨板内的长度不可按常规设计中小板短跨的1/4设置，应按需加长。

⑷ 四周主梁处的楼板支座筋伸入大跨组合楼盖板跨内的长度应按实际所需取值，如按常规设计中次梁分割后小板短向跨度的1/4取值，会与实际有较大偏差。

⑸ 竖向荷载作用下，梁板中线对齐模型无法正确反映楼板轴力拉压变化的规律。

⑹ 与梁板中线相对偏移模型的配筋结果比，梁板中线对齐模型大部分区域底筋和外围支座筋偏大，中间区域支座筋偏小；查表法结果整体偏小很多，无法满足楼盖的整体受力所需。

⑺ 框架柱附近的楼板支座筋长度需要适当加大。

⑻ 本工程大跨钢-混凝土组合楼盖的竖向自振频率与加速度均满足文献［13］的限值要求。