射流式离心泵气液两相流数值分析

王维军，李泰龙

（航空工业成都凯天电子股份有限公司，成都 610091）

0 引言

近些年，随着计算机技术、湍流模型、两相流模型等硬件、软件设施的快速发展，通过CFD技术模拟、分析泵内气液两相流动成为一种十分必要的手段，学者们在这方面做了大量的研究。李清平［1］采用气泡轨迹模型计算了不同初始大小，不同进口位置的气泡在离心泵和螺旋轴流泵叶轮内部的运动情况，得到了气相在叶轮中的流动轨迹和受力情况；Rudolf S［2］采用双流体模型数值计算了离心式叶轮内部的气液两相流场，得到了较满意的结果；卢金铃等［3］、马希金等［4］使用双流体模型按不可压等温流动假设给定出口边界条件分别计算了离心泵叶轮和螺旋轴流式叶片泵内的气液两相流。黄思等［5］利用FLUENT流场模拟软件采用欧拉方法的双流体湍流模型计算了螺旋轴流式叶片内高含气状态下的三维气液两相流场，探讨了气液两相流介质在泵内的流动规律。王春林等［6］采用雷诺时均 N-S方程、RNG k-ε湍流模型和多相流模型对自吸旋流泵做了数值模拟，得出液相速度略大于气相速度，靠近泵进口的两叶道内含气率较高等结论。李红等［7］运用Mixture模型对自吸式喷灌泵自吸过程做了数值模拟，得出叶片吸力面的相对速度和含气率都要大于压力面。

射流式离心泵在启动和大流量等工况下存在着复杂的气液两相流动，气液两相流中存在可变形的界面，两相之间存在滑移速度，使泵内流动产生振荡［8-9］，效率下降，影响着流动连续性。

1 控制方程

目前数值模拟两相流有2种方法：（1）欧拉法，即将某相看出是连续的，根据连续性理论推导出欧拉型基本方程；（2）拉格朗日法，即将某相视为不连续的离散型，对每一个质点进行拉格朗日追踪。

本文在模拟射流式离心泵气液两相流动过程中把液相作为连续相，气相作为离散相，选用Particle模型，即欧拉——欧拉多流体模型来描述气液两相流之间的相互作用。控制方程对液相（连续相）的湍流模型采用RNG k-ε双方程模型［10-11］，气相（离散相）采用零方程模型。

2 求解模型

本研究射流式离心泵的基本参数为：设计流量Qd=3 m3/h，设计扬程Hd=32 m，额定转速n=2 900 r/min，比转速ns=22，泵效率15%，吸程8.5 m。过流部件尺寸：泵进口直径Ds=40 mm，叶轮外径D2=159 mm，叶轮进口直径D1=40 mm，叶轮出口宽度b2=4 mm，叶轮叶片数Z=6，导叶基圆直径D3=161 mm，导叶宽度b3=12 mm，导叶外圆直径D4=184 mm，导叶叶片数Z=6，喷嘴直径djet=10 mm，喷嘴总长148 mm。射流式离心泵模型如图1所示。随着节点数和网格数增加扬程逐步下降，当扬程相关性低于0.5%时可以认为网格对计算结果无影响，最终确定网格节点总共为702 008，网格数总共为3 009 149。

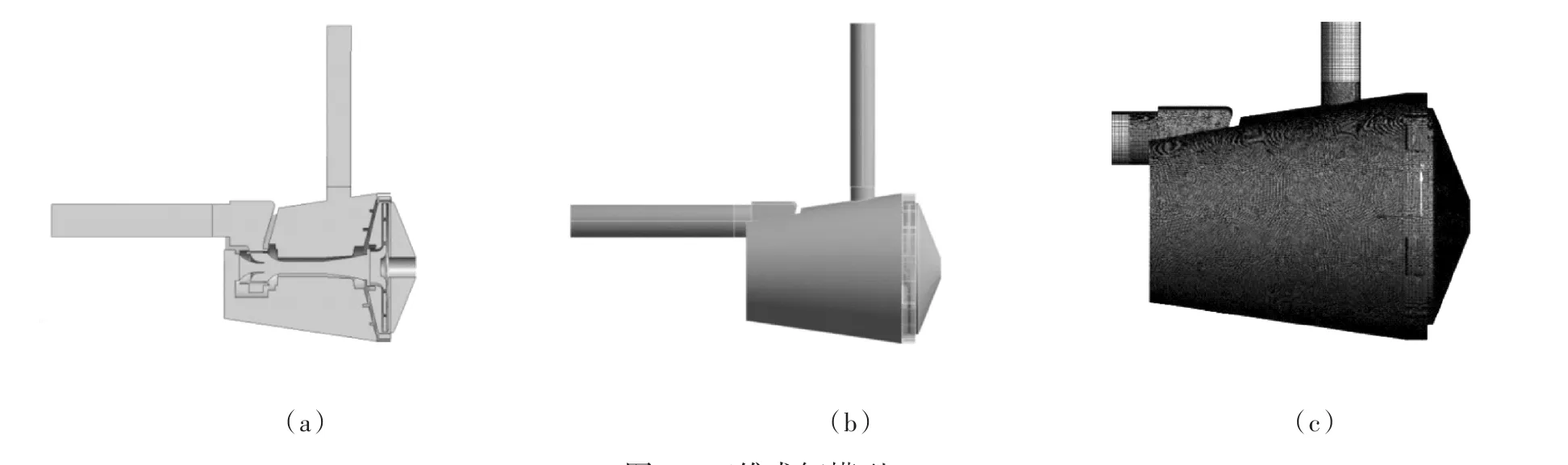
图1 三维求解模型

3 边界条件的设置

两相流计算的基本参数为：在计算域进口第一相为清水，第二相为空气，假设进口含气率均匀分布，气体的含气率αg分别为 0.05，0.10，0.15和0.20，气泡直径为0.1 mm；总压进口，设定压力值为1.01×105Pa，湍动能强度设为5%；采用质量出口条件；近壁区使用伸缩壁面函数（Scalable Wall Functions）处理。采用Frozen Rotor冻结转子法。

4 气液两相流数值模拟结果分析

本文数值模拟了 Q=0.5，1.0，1.5，2.0，2.5，3.0 和3.5 m3/h 7种工况下的内部流动。图2示出试验结果和数值模拟结果对比曲线，在设计工况下，数值模拟的结果高于试验结果，扬程、轴功率和效率的相对误差为2.63%，6.16%和14.29%，这是因为在数值模拟过程中仅仅考虑了湍流造成的损失，忽略了轴承、摩擦副等引起的机械损失；试验值在Q＞3.5 m3/h工况后各个参数的试验曲线发生了突降，该工况与低比转速离心泵大流量工况特性类似［12-20］；从图2（b）中可以看出，当流量Q＜3.5 m3/h时数值模拟和试验测试的轴功率均近似呈水平直线，没有出现最大值。从图2（c）中可以看出，泵的最大效率为Q=3.5 m3/h工况时的15.68%。本文采用的网格和湍流模型可以较准确预测出射流式离心泵小流量工况和设计工况下的外特性变化。

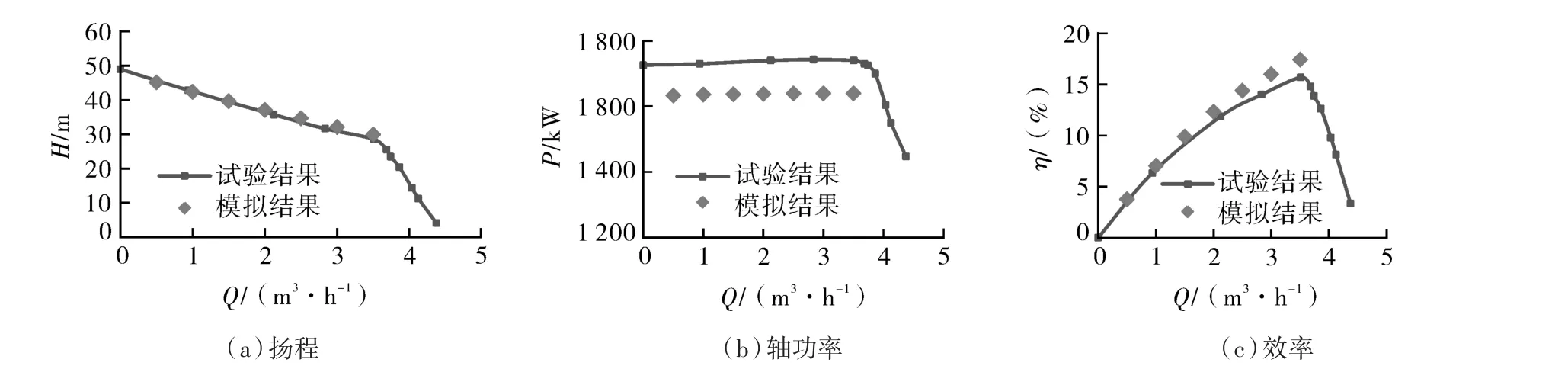
图2 数值模拟和试验结果对比关系

4.1 设计工况下全流场压力分布

设计工况下当含气率αg＞0.10时，外特性下降明显，尤其是扬程的变化十分明显，含气率为αg=0.05时扬程为30.5 m，比单相计算时的扬程仅减小1.5 m，而当含气率αg=0.10时扬程已经下降至15.4 m，大大低于此时的单相计算扬程。从图3可以看出泵腔内二者的压力几乎相差一倍，压力区的位置均在射流器直线段，压力值在2.7～5.2 kPa之间。因此，泵内含气率的增大是导致扬程下降的主要因素之一。

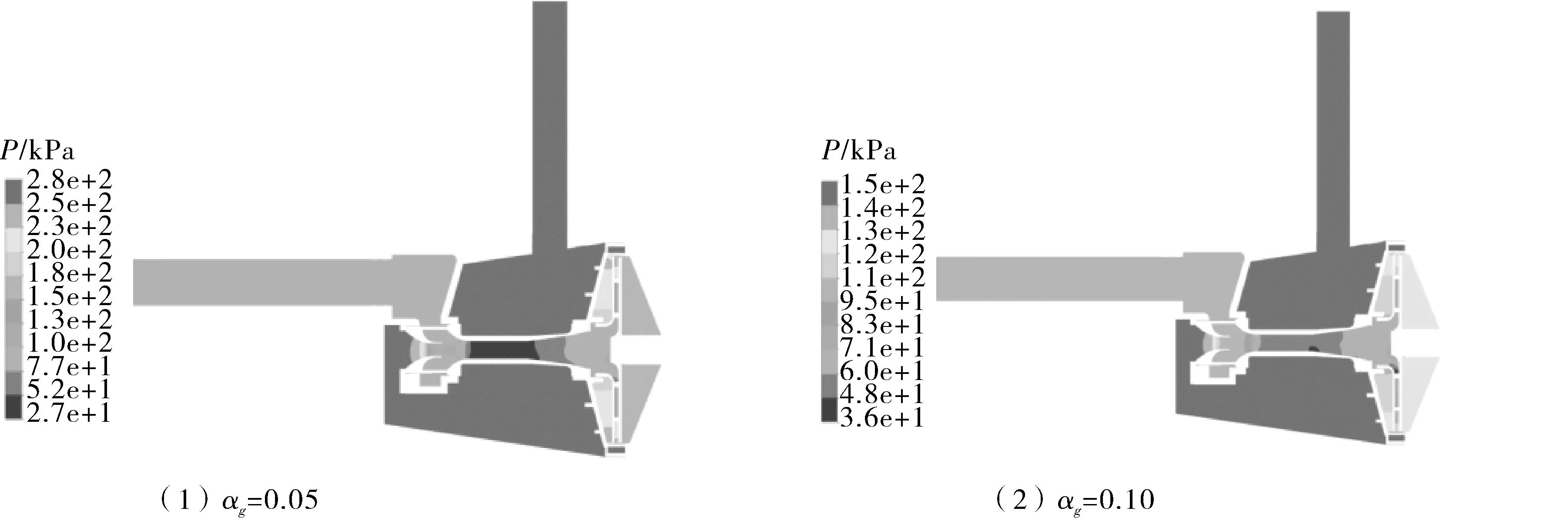
图3 不同含气率下静压分布

4.2 设计工况下泵腔、射流器内含气率分布

图4 示出设计工况下4种含气率时泵腔、射流器内的气相分布云图。从图可以看出，当含气率αg=0.05时，气相主要集中于射流器喷嘴和扩算段两个区域，且由于重力的影响，气体位于射流器上方，吸入段出现了少量的气体；当含气率αg=0.10时，整个泵腔的含气率在0～0.5之间，吸入段已经出现了断流，出口位置出现了少量气体；当含气率αg=0.15时，射流器中的气体继续增加，靠近叶轮进口侧已经有一般被气体占据，进口段间歇式的断流明显加剧；当含气率αg=0.20时泵内已经大部分被气体占据，尤其是后泵腔和出口段内，吸入段的断流进一步加剧，含气率达到了0.7。

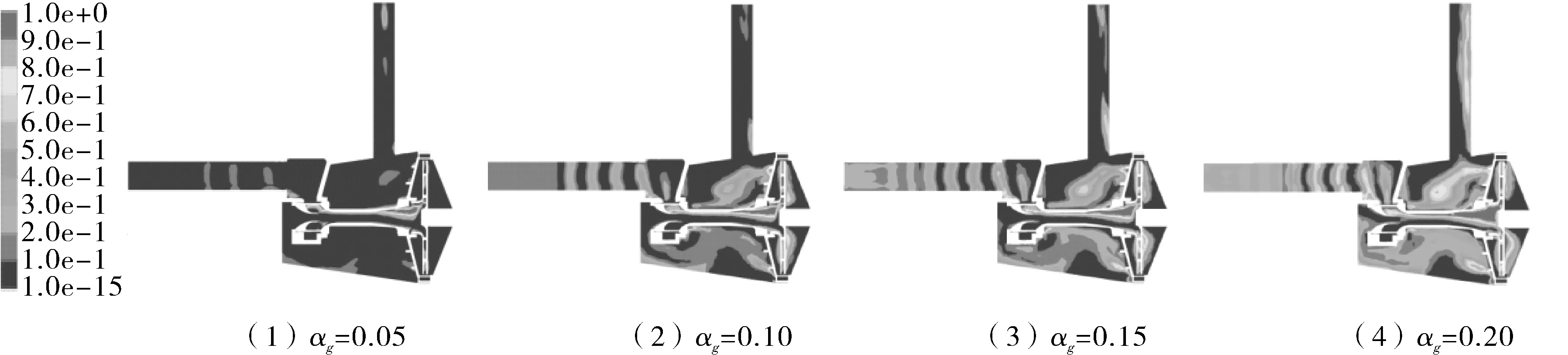
图4 不同含气率下的气相分布

4.3 设计工况下泵腔、射流器内气相速度分布

图5 为设计工况下4种含气率时泵腔、射流器内的气相绝对速度分布云图。当含气率αg=0.05时，气相绝对速度最大值分别为29，22和22 m/s，最大速度区均在喷嘴出口处，射流器直线段之前的速度变化比较平缓，在扩算段中气相较混杂，速度分布也不是轴对称；当含气率αg=0.10时，喷嘴处的最大速度已经降到了12 m/s左右，此含气率下也是扬程变化较大的时候；当含气率αg=0.15和0.20时，射流器中的气相速度已经降到了6 m/s以下，此时高速液流和低速液流的混合程度已经大大降低。

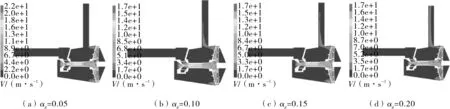
图5 不同含气率下的气相速度分布

4.4 不同工况下叶轮内部气相体积分布

图6 为不同工况下叶轮内部气相体积分布，不同工况下当含气率αg=0.05时气相主要聚集在一个叶道中，且大部分气体在该叶道靠近叶片吸力面的位置处，而其他5个叶道中存在一部分气体，越靠近气体聚集叶道时，该叶道的气相体积越大；当含气率αg=0.05～0.15时，3个叶道中的气体体积分数接近了1，几乎完全被气相占据，该3个叶道中的液体必然也会发生断流现象，而其他3个叶道的气体体积分数也在0.5左右，因此外特性的变化是必然的。当含气率αg=0.2时气体几乎完全占据了整个叶轮，小流量工况下尤为明显。

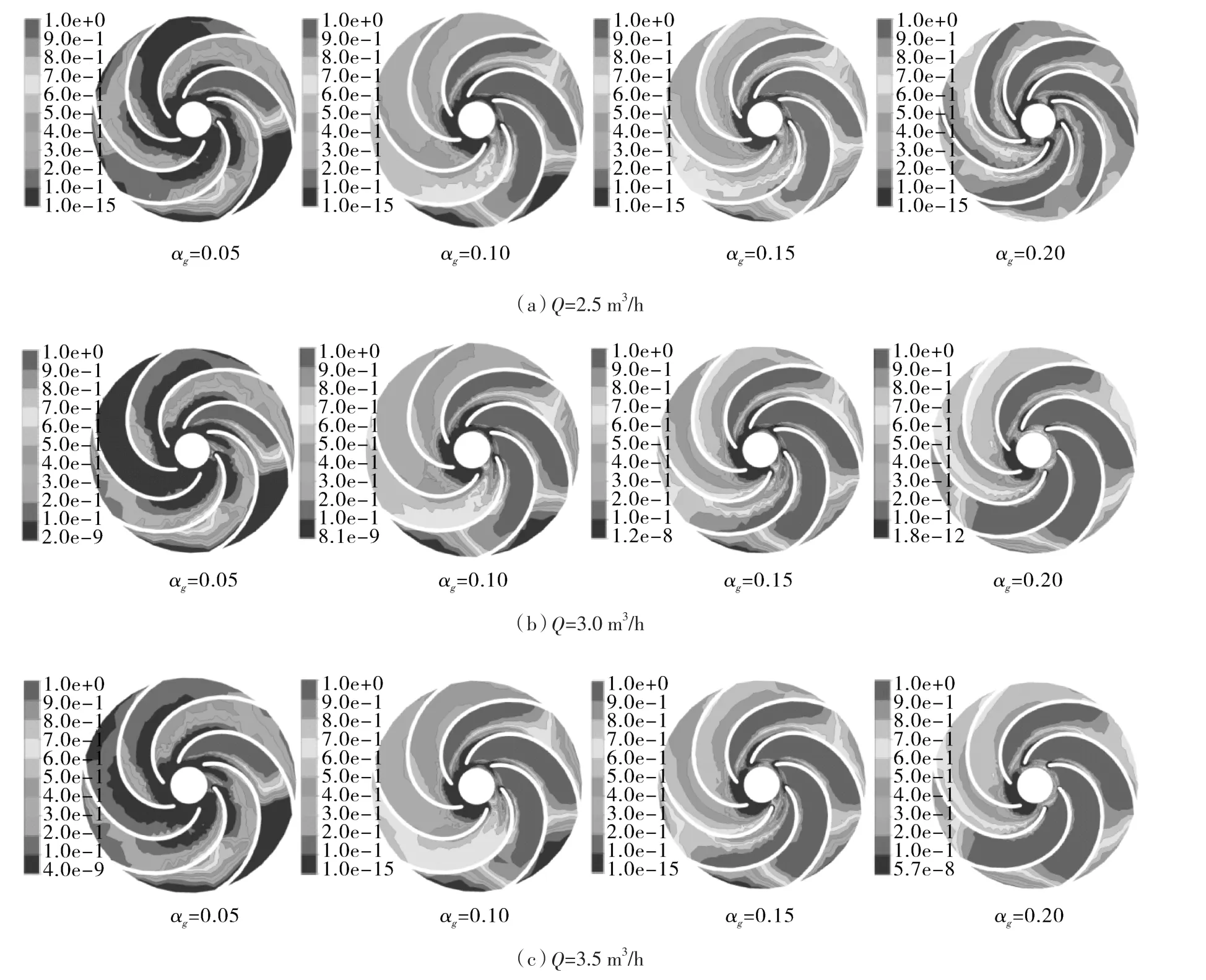
图6 不同含气率下叶轮气相分布

4.5 射流器中气液两相速度差分布

为了分析设计工况下不同含气率时射流器中气液两相的速度变化，本文监测了沿着轴线从喷嘴到叶轮进口距离L之间的速度。从图7可以看出，靠近叶轮进口处的速度在5～7.5 m/s之间，在含气率αg=0.05，L=20～90 mm液相速度大于气相速度，速度变化较平缓，气液两相速度差为1～2 m/s；在 L=90～150 mm 时气相速度大于液相速度，两相最大速度差为4 m/s；含气率αg=0.05在L=150～190 mm时液相速度大于气相速度；含气率αg=0.05下的两相速度远大于其他含气率下的速度；在喷嘴L=150 mm距离处气相速度变化较大，气相速度曲线在此处出现了驼峰，液相速度始终是均匀变化。

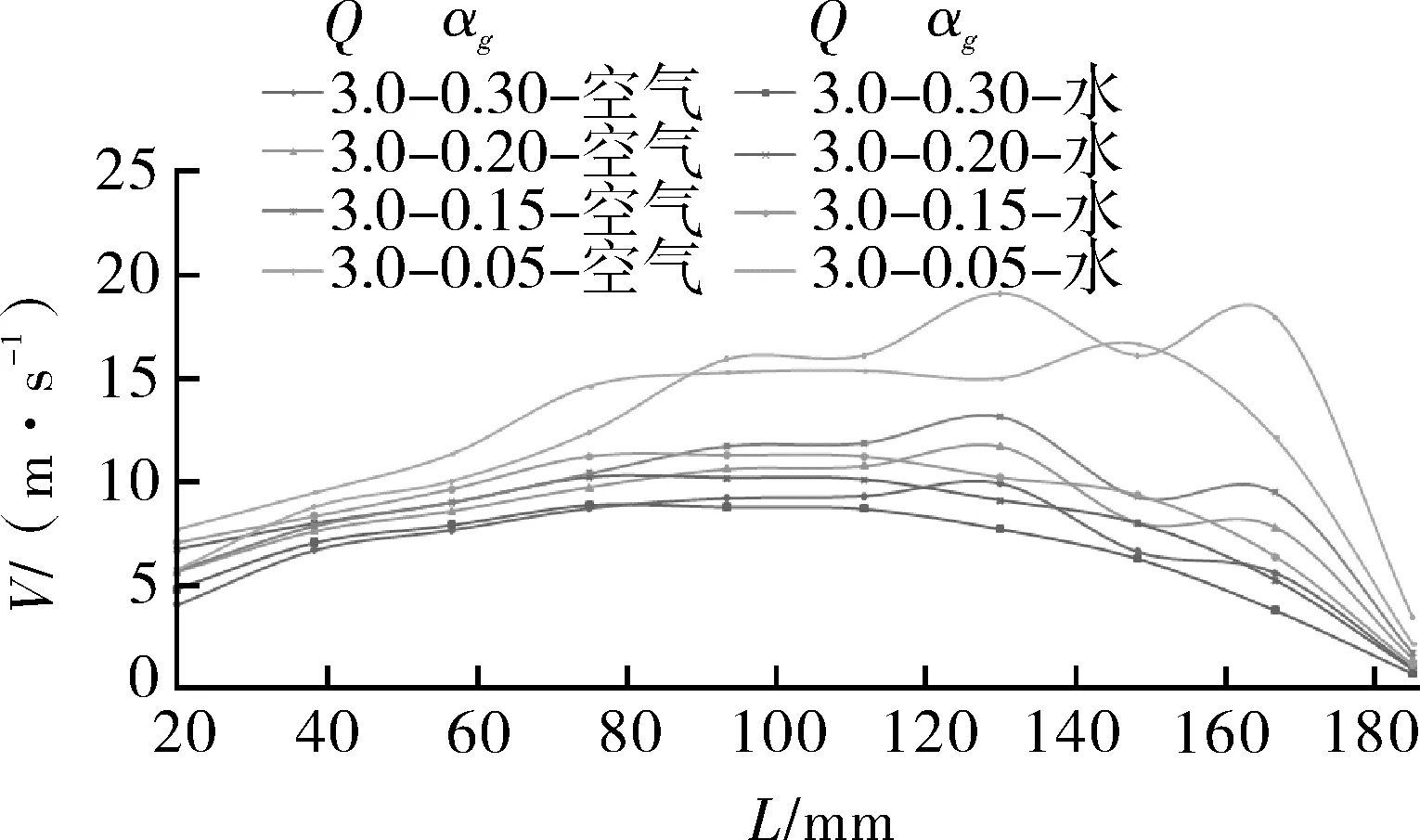
图7 不同工况下射流器中气液两相流速度分布

5 结语

在单相定常收敛的基础上数值模拟了射流式离心泵气液两相全流场，分析了叶轮、射流器内部的含气率分布、气液两相的速度差和压力分布等。结果表明：泵进口含气率αg=0.05 是泵性能发生变化的临界含气率点；射流器中的气液两相存在着明显的速度差，在喷嘴到叶轮进口的距离为20～92 mm与150～190 mm两个区间内液相速度大于气相速度；气液两相混杂流动导致流动断续是造成大流量工况下扬程突降的主要因素。