一道高考向量题多种解法的思维切入点

云南省昆明市第三中学 (650500) 张兴锋

对高考试题的研究是中学数学教师进行教研的重要内容.笔者深入研究了2017年全国卷Ⅲ理科第12题的解法,本文将从平面向量的核心知识点出发给出该题的几种解法,并指出各种解法的思维切入点.希望能给读者一些启发.

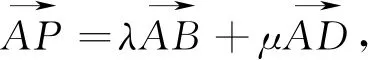
分析:高中阶段,平面向量的运算涉及到了线性运算与数量积运算，而这两种运算又分别可以从几何与代数的视角进行处理.为了表述的方便,我们先作如下约定:

如图1，设M为圆C与直线BD相切的切点,直线MC与圆C的另一交点为N,直线MC与AD的交

图1

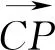
切入点一：平面向量的线性运算

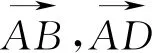
点P在直线B′D′上⟺(1-λ)+(1-μ)=

-1⟺λ+μ=3.由点P在以C为圆心且与BD相切的圆上知点P在直线BD与直线B′D′之间,故λ+μ∈[1,3].

切入点二：平面向量的数量积运算

评注：由于两次应用不等关系,而且两次不等关系中取等号的条件不同,因此此法得到的数值不是其最大值.即是说,以上解法有误.

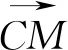
解法7：由①得

解法8：由②得

[-1,1],因此λ+μ∈[1,3].

切入点三：平面向量的坐标化运算

由ABCD是矩形不难想到建立平面直角坐标系,进而将平面向量的运算进行坐标化,最后转化为代数运算进行求解即可.

一题多解是训练学生思维能力的好办法,但问题的关键在于如何引导学生理解并掌握一题多解中各种方法的切入点.本文以一道高考试题为载体进行了尝试,希望读者能体会到各种方法都是基于平面向量最核心的知识点挖掘而来.