基于临界滑动场法深基坑排桩桩间距的探讨

张琛，朱大勇

（1.合肥工业大学，安徽 合肥230009；2.浙江大学宁波理工学院，浙江 宁波315100）

1 引言

排桩支护系统作为一种传统的深基坑支护形式，由于其施工便利又可以和内支撑结构、地下连续墙、锚杆系统等其他支护形式相结合，在深基坑工程仍被广泛采用。

国内外关于支护桩桩间距设计与计算的相关研究以护坡桩居多，相关理论对于深基坑排桩的桩间距设计与验算都有着一定的借鉴意义。深基坑排桩支护桩间距的影响因素主要包括：①排桩支护结构自身要保证必要的强度和刚度；②支护系统要满足整体的抗滑稳定性与抗倾覆稳定性；③桩间土要满足局部稳定性。在设计和验算桩间距时若仅考虑前两点则结果偏于保守，造成资源的浪费；文章基于临界滑动场法通过验算桩后土体局部稳定性，提出验算排桩间距较为合理的方法。

2 深基坑开挖面以上土体的应力分析

2.1 桩后土体应力状态

基坑开挖面以上的土体往往受到竖向应力σv以及水平向的土压力p。对于排桩支护的基坑，水平土压力p可根据土体的位移趋势不同，分为沿着位移方向的主动土压力pa，以及垂直于位移方向的静止土压力p0。对于基坑外侧有超载或埋深足够大的土体，有σv＞p0＞pa，三者相互正交。对于开挖面以上的桩后土体单元有σ1=σv、σ2=p0、σ3=pa，三者关系的应力莫尔圆如图1所示。

图1 主动状态应力莫尔圆

实际施工过程中基坑外侧都存在不同程度的超载，如图2所示，对于开挖面以上的桩后土体，每一个土体单元均受到竖向与水平的压应力。相较于水平向的正应力而言，竖向的正应力σv较大，假设σv作用面正是主应力作用面，即有σ1=σv，此时两个较小的正应力σ2与σ3的作用方向就处在水平面上，由静止土压力与主动土压力定义：σ2=pa、σ3=p0。

由于桩身摩擦的存在，土体在桩表面附近的主应力方向往往会发生偏转，C.-Y.Chen[1]等使用FLAC软件对抗滑桩进行数值模拟，得到了桩周应力偏转较为直观的现象。为验证这种现象在深基坑中同样存在，作者使用FLAC3D建立了一个横断面如图2所示的模型进行模拟计算。模型桩长20m、桩身截面为正方形边长0.8m、桩中心间距2m、无圈梁及水平支撑；开挖深度10m，分5次开挖，每次开挖深度为2m,基坑外侧超载30kPa。土体与支护桩均为实体单元，桩土界面设置为刚性接触面，模型各参数见上表。

图2 深基坑开挖计算截面

模型计算参数

模型计算完成后调出主应力张量（Tensor of Principal Stresses），需要说明的是FLAC3D软件中默认拉应力为正，这与土力学中的符号约定相反，因而显示的最大值应为最小主应力σ3。图3-a、3-b即为开挖深度2m左右时，开挖面附近的桩后土体σ2与σ3的应力偏转现象。这可能是由于支护桩的水平反力与侧向摩阻的存在，使得桩周土体产生不均匀的位移。

图3 水平截面应力偏转迹线

2.2 土体的三维应力状态下的破坏面

根据莫尔-库仑强度理论，土体在临界滑动面与σ1作用面成夹角，其中φ为土体内摩擦角。实际工程中土的应力状态是三维的，松冈元等[2-3]认为土体在临界状态下的空间滑动面SMP是三个主应力作用下的滑动面组合而成。如图4-a所示，在临界状态下，对于每一对σi＞σj（i，j=1、2、3下同）都有组滑动面，且与σi作用面夹角为其中φmoij=arcsin。对于砂土而言，三个主应力的莫尔圆如图4-b所示，而土体的整体空间摩擦角为：

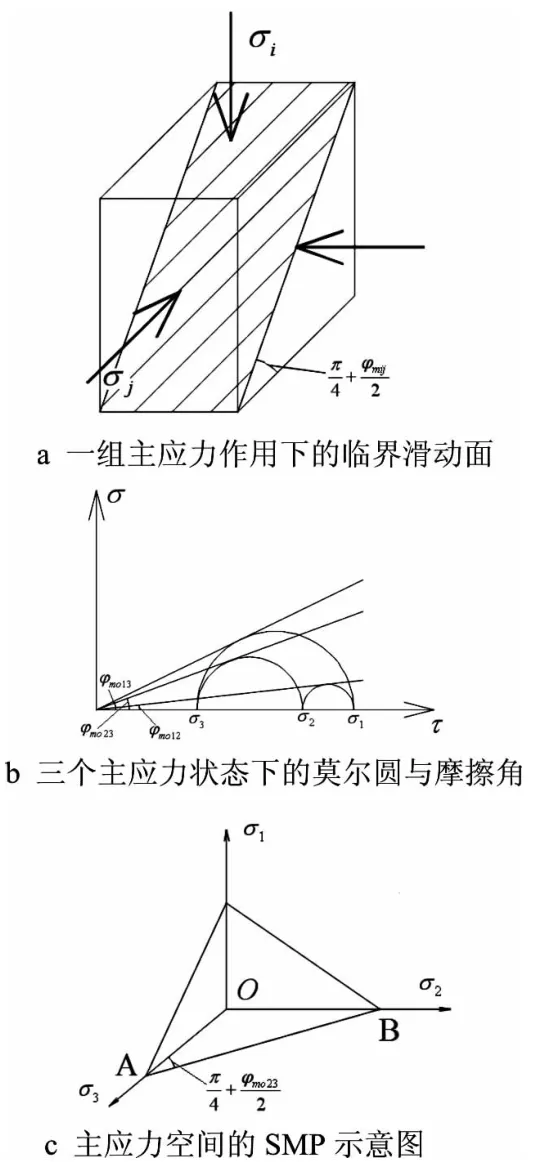
图4 空间应力下的滑动面与莫尔圆

如图4-c所示，整体滑动面SMP与σ1作用面交线为AB，σ2作用面与σ1作用面交线为OA，AB与OA夹角为，其中。实际问题中σ1作用面为水平面，σ3→0时，由式1可知，即SMP垂直于σ2作用面；当σ3=σ2时，φmo23=0，即φSMP=φmo13=φmo12=φ，整体空间滑动面与φ作用面夹角为0，土体在σ2与σ3作用下不发生整体滑动破坏，此时即为二维的莫尔-库仑准则。

如前所述，基坑开挖过程中除了大主应力σ1作用下发生的桩后土体整体滑动破坏，还有中主应力σ2与小主应力σ3作用下的局部破坏。由图4-b易见φmo13≥φSMP≥φmo23，因而土体在局部破坏时水平面滑动面上受到的剪应力τmo23=c+σ·tanφmo23与土体整体滑动面上的剪应力τSMP=c+σ·tanφSMP的关系为τmo23≤τSMP。可见对于各向同性的土体水平面上的局部破坏要先于整体剪切破坏，这实际上取决于中主应力σ2与小主应力σ3的方向与相对大小。

2.3 桩间土拱的形成条件与边界的简化

Terzaghi提出的了土拱形成的两大条件[4]：一是土体存在不均匀的位移或相对位移；二是存在提供支撑力的拱脚。贾海莉等[5]又在其基础上增加一项条件，即土拱形成范围内的土体剪应力小于其抗剪强度。这说明对于桩间的水平土拱而言，土体的剪切破坏只发生在土拱的前缘与后缘。正是由于桩后水平土拱的存在使得桩后土压力全部或绝大部分由支护结构承担，从而保证了桩后土体不会局部失稳破坏导致支护结构失效。

上述的三个必要条件中的一个或几个发生了破坏均会导致桩后水平土拱无法形成或发生破坏：①土体的不均匀位移消失，土体无位移趋势或者支护形式为地下连续墙、SMW工法桩等连续支护形式，减弱或消除了水平面上的不均匀位移；②支护结构无法提供形成拱脚的支撑力，这种情况可能是桩身结构发生破坏或基坑整体滑移或者倾覆；③土拱范围内的土体发生剪切破坏，使得土拱的几何性状发生破坏。其中最后一项可以认为是土体局部失稳的主要原因。

3 临界滑动场求解过程

3.1 桩后土体的水平临界滑动场

如图5-a所示，桩后土体在临界状态下，可能产生两簇共轭的滑动面。其中有一组滑面对相邻两桩之间土体稳定性起决定作用，如图5-b所示，在右侧桩OA向左侧发展的滑动面中，从A点出发的滑动面是两桩之间的控制滑动面，其扩展的最远距离就是临界状态下桩后土体局部破坏的最大范围。

图5 桩后水平临界滑动场

3.2 桩后土体临界滑动场的相互影响

设相邻的两根桩的迎土面宽度B、净桩距L以及临界滑动面最大宽度X等三个参数可以分为如图6的4种情况来讨论：

图6 相邻两桩的临界滑动场扩展范围

③L＋B＜X＜L+2B，如图6-c的情况，相邻两桩的临界滑动场充分重叠均落在相邻桩身范围内，此时土体抗剪强度都得到了充分发挥，满足了土拱构成的三个必要条件。临界滑动面后缘连线即为桩后水平土拱的后缘，也近似于应力偏转的迹线。

④X＜L+2B，此时一根桩的临界滑动场范围超出了相邻桩的桩身范围，如图6所示，设想如果g1与g2点的距离足够大，已经达到或者超过第三根桩的桩身范围，那么相邻两桩的支护作用就接近于一个整体。

3.3 实现方法与计算程序

桩后土体在水平面上划分为若干条块，条块划分及相关参数如图7所示，其中第一个条块是朗肯主动区，对应的，该条块的受力情况可以通过经典的弹塑性理论求得。

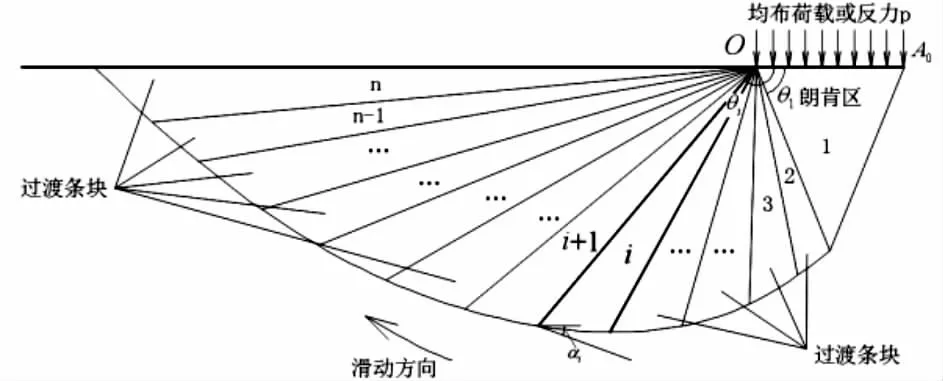
图7 条块的划分与受力分析

为满足条块的滑动条件总有底边的倾角αk＜αk-1，并规定水平线向逆时针方向转动为正。条块受到的主动土压力合力Qk，条块底边黏聚力Ck，条块底面反力Rk。条块的k、k-1边界受到的推力分别为Pk-1、Pk，作用点与O点距离分别为zk-1、zk；推力与作用面垂线的夹角分别为δk-1、δk。夹角δ是条块边界倾角θ的函数，二者关系如式2所示：

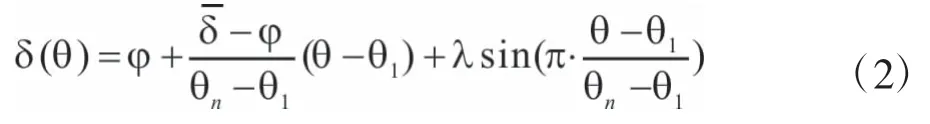
由条块受力平衡条件可以得到Pk与Rk的递推公式：

如果只考虑条块力的平衡，那么只需满足式3与式4。若考虑力矩平衡，则有：

由式2可知Pk及Mk也是λ的函数，可以通过通过Newton-Raphson法迭代求解或试算确定λ。若只考虑力的平衡条件，则条间最大推力max(Pk)所对应的αk即土体产生破坏时最有可能的滑动倾角，由于主动临界滑动场对条间力函数并不是十分敏感[6]，通过试算得到的λ结果也比较理想。

作者利用Matlab数值处理软件对上述过程进行可视化编程，将计算区域以O点为中心分为n个条块，每个条块边界上设置m个状态点，这样每个条块的几何参数就可以由上一个条块状态点的坐标和条块倾角αk确定。

这里需要讨论一下αk的取值范围：由于滑动面要保证其位移连续性，每个条块底边倾角上限为上一个条块的倾角，即αk＜αk-1；而下限则是土体在σ2与σ3作用下产生的极限破坏面的倾角，即。可以让αk在上下限之间以为步距进行搜索，求得的αk应使得Pk达到最大值，即式6方程的根：

通过α以及滑动面的起点坐标就可以得到特定条件下的滑动面，这条滑动面是桩后水平临界滑动场的最大范围。以下分析中无特殊说明，所述φ均应为φmo23。

4 计算结果分析

4.1 临界滑动场范围对参数的敏感性

执行计算程序，通过调整土的摩擦角、黏聚力c，可以得到不同的临界滑动面最大宽度X以及最大扩展高度Hy。由于临界滑动面的最大宽度X受到桩身宽度B的影响，同时也是计算合理桩间距的重要指标，因而以下的讨论中将二者比值X/B作为一个指标进行考虑。这种比较与计算的前提，是不考虑相邻两桩的水平面临界滑动场相互干涉与扰动。

由图8-a、8-b可见，临界滑动面的最大宽度与最大高度都随着摩擦角的增加而显著增加，当内摩擦角φ=40。时，X/B=5.18，即临界滑动面的最大扩展范围已经到达5倍桩径以上，而扩展高度即临界滑动场向桩后土体扩展的纵深也达到1.14m。土体的粘聚力从5kPa增加到40kPa过程中X/B几乎没有发生变化，这说明桩后土体的临界滑动场扩展范围对内摩擦角φ非常敏感，而受到土的黏聚力c变化影响较小。

图8 临界滑动面扩展范围与土体参数关系

4.2 临界滑动场后缘的影响

临界滑动场实际上是一个作用范围其存在前缘与后缘，如图9-a所示，临界滑动面后缘的边界可以认为是临界状态下临界滑动场所能影响到的最大范围。

图9 临界滑动场的范围及其随摩擦角φ变化

图9-b为计算程序绘制出土体的内摩擦角从5。变化至40。时相邻两桩的临界滑动场后缘范围。可见当桩距固定时随着土的摩擦角不断增大，相邻两桩的临界滑动场相互交叠的区域越大；而对于特定的内摩擦角，相邻两桩中心距存在一个临界值Lc，即当桩中心距小于该值时，两桩的临界滑动场发生相互扰动，即图6-b～6-d所示的情况。

沈珠江指出[7]，当桩间距小于某临界值Lc时，相邻两桩的绕桩阻力的应力迹线会发生扰动，绕桩阻力无法通过解析表达式求得并需要通过数值方法求解，这个临界桩间距的表达式为：

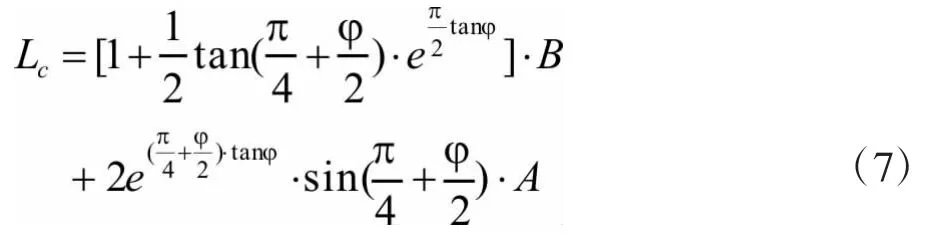
式中A、B分别为抗滑桩的迎土面宽度与侧面宽度，对于不考虑桩侧摩阻则可令式中A=0得：

使用文章方法与式13方法分别对桩截面宽度B为0.8、内摩擦角φ分别为5～40砂土的临界桩间距进行验算，结果如下图所示：

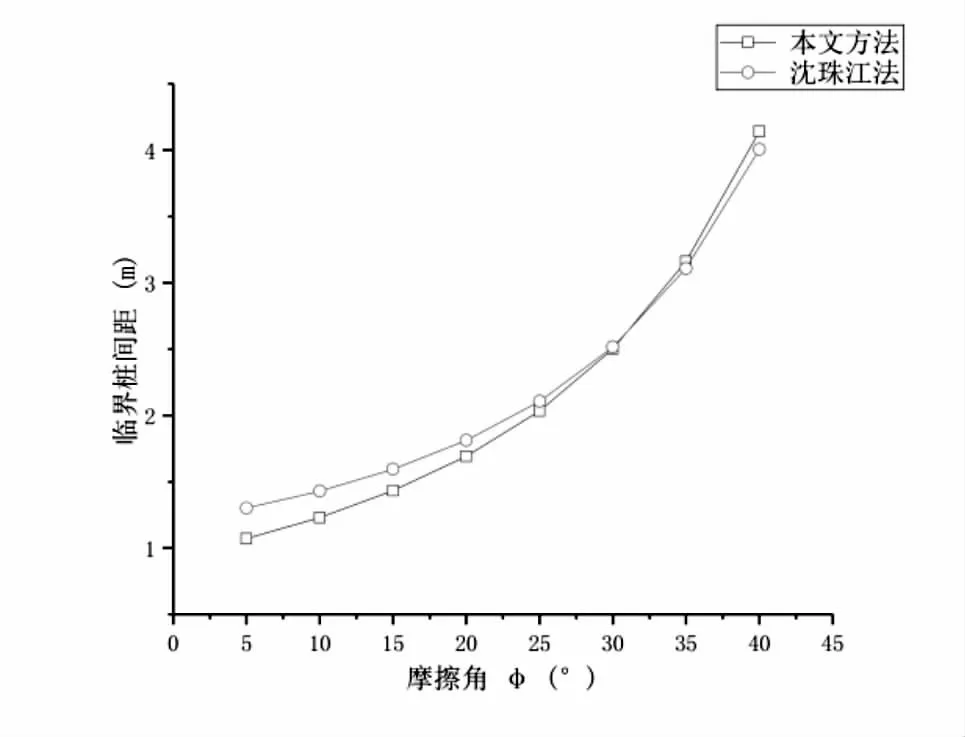
图10 临界桩间距与摩擦角φ的关系

可见当φ＞20。时，Lc会变得很大，甚至达到桩径的4倍以上，此时单靠临界滑动场后缘的范围是不足以判定合理桩间距的。

4.3 临界滑动场前缘的影响

如果不考虑两桩之间土体的抗剪强度以及桩身的侧向摩阻，那么桩后土体水平临界滑动场的前缘只有φ在大于一定值时才会出现。这种情况下，如图9-a所示，在临界滑动场前缘以外的土体是作为一个整体，如果前缘线能够到达相邻桩身范围，那么之后的土体就能够受到一定程度的支挡。

图11 临界滑动场前缘、后缘范围与摩擦角φ关系

通过执行计算程序，对于不同的φ，临界滑动场扩展距离与X的比值如图12所示，当时φ≤20。，前缘的范围在一倍桩径以内；而当φ＞20。时其扩展范围随φ的增加而增加，并且随着φ的增大，临界滑动场的前缘与后缘最远扩展距离差距也则不断增大。

如前所述，对于φ≤20。的土体（或者严格来说是φmo23≤20。），水平面上的临界滑动场扩展范围较小，相邻桩的临界滑动场交叠干涉范围也较小，可以从临界滑动场的前缘位置来判定合理桩间距，这是桩间距一般都在1-2倍桩径。

4.4 整体稳定性的影响

胡敏云等[8]认为，在桩间水平土拱完全发挥作用时，最大桩间距S是摩擦角的函数，其表达式为：

S是一个关于φ减函数，贾海莉在研究抗滑桩间水平土拱时也得到类似的规律[9]。这里的φ应当是水平面上的摩擦角φmo23，这种情况下桩后土体由于水平土拱的作用，局部处于非极限状态，那么基坑的破坏就是一种整体失稳破坏。若将文章方法求得的临界滑动场后缘范围视作局部极限状态下的最大桩间距，对于B=0.8，二者关系如图12。

图12 基于整体稳定性与局部稳定性最大桩间距的比较

综上所述，考虑土体整体稳定性对排桩合理间距的影响要综合基坑深度、破坏形式以及桩间土拱的强度储备三个方面考虑，结合桩间土体的局部稳定性以及一定的安全度，桩间距设置在2倍桩径左右是较为合理的，这也与现行规范的规定相符[10]。

5 结论

①对于深基坑排桩支护结构，桩间土体存在水平的临界滑动场，临界滑动场的各项参数与土体的中主应力、小主应力的方向及相对大小有关；

②桩间土体的局部稳定性受到临界滑动场的影响，且临界滑动场的范围对土体在水平面上的摩擦角φmo23非常敏感，相邻两桩的临界滑动场在一定范围内会出现互相交叠与扰动；

③对于摩擦角较小的土体，即φmo23≤20。，桩后土体的局部稳定性对桩间距的影响较大，可通过执行作者所编写的程序可直接输出建议的合理桩间距；当土的摩擦角较大时，即φmo23≤20。时需要综合考虑支护系统的整体稳定性，局部稳定性则仅作为参考。

④由于文章的方法是对临界滑动场理论应用范围的一次扩展，对深基坑排桩支护结构的几何模型以及力学模型均作了一些简化，因而存在一些地方不精确的地方，今后可以通过优化计算程序来提高计算准确性及实用性。