一种可抑制航向运动影响的单轴转位方案

(西安航天精密机电研究所，西安 710100)

0 引言

旋转惯性导航系统[1-3]是通过在惯性测量单元(IMU)外加上转位机构和测角装置，控制IMU按照一定的次序旋转，使陀螺漂移和加速度计零偏对导航产生的误差能够在一个转动周期内抵消，从而提高系统导航精度。旋转调制技术可以在现有惯性器件精度的基础上提高系统的导航精度和自主性，是高精度导航系统常用的技术手段[4-5]。单轴旋转调制惯导系统的转位机构转轴与载体天向轴重合，在载体静止状态下可以消除垂直于旋转轴方向上的惯性器件误差，但是当载体做航向运动时，载体的航向运动与转位机构带动IMU的旋转会叠加，使得IMU不能按照预期在整周期内抵消误差，从而降低旋转调制的效果[6]。目前常用的单轴调制方案有双位置和四位置，文献[7]通过仿真和实验验证了双位置和四位置调制效果相近，本文在双位置调制方案的基础上设计转位方案。

为了隔离载体航向运动对旋转调制效果的影响，目前普遍利用解算得到的姿态数据驱动转位机构运行隔离航向运动，使IMU在转位停止的过程相对导航系航向角不变。文献[8]提出了一种基于载体姿态解算驱动IMU转台的抑制方法。以上方案都能够有效地抑制载体航向运动的影响，但由于载体航向角往往频繁变化，为了控制IMU航向角保持不变，转位机构的电机就会不停地启动和制动，使其寿命大大减小。本文在传统双位置旋转调制方案的基础上，根据实时解算的IMU航向角，控制IMU相对导航系的旋转角度在每个周期内进行调整，从而有效抑制载体航向运动对IMU常值误差调制效果的影响。此方案相对传统双位置旋转调制方案并没有明显增加旋转次数，每个周期内的停止时间相同，避免了电机的频繁启动和制动，在抑制航向运动影响旋转调制效果的同时没有减小机构寿命，具有工程应用价值。

1 旋转调制技术基本原理

定义s系为IMU坐标系；b系为载体坐标系，坐标轴方向为右前上；n系为导航坐标系，坐标轴方向为东北天；i系为地心惯性坐标系。

陀螺和加速度计的输出：

(1)

则陀螺和加速度计的输出误差为(略去二阶小量)：

(2)

下面以陀螺常值漂移为例说明旋转调制的基本原理。

假设初始时刻，s系，b系和n系重合，如图1所示，导航坐标系中等效陀螺漂移为：

(3)

图1 旋转调制原理

假设b系与n系始终重合，将s系绕z轴旋转180°之后，导航坐标系中等效陀螺漂移为：

(4)

由以上两式可知，s系绕z轴旋转180°后，等效东向和北向陀螺误差的符号由正变为负，假设陀螺三个轴的漂移不随时间变化，则在这两个位置上由x，y陀螺引起的导航误差在相同的时间内会相互抵消。而等效天向陀螺漂移的符号未发生变化，因此由z陀螺引起的导航误差没有被消除。

在旋转过程中，假设s系绕z轴以角速度ω匀速旋转，则s系到b系的转换矩阵为：

(5)

在n系下的等效陀螺漂移为：

(6)

可见，在旋转过程中等效东向和北向陀螺漂移被调制成周期变化的量，若在一个调制周期内s系绕z轴旋转360°，则在导航系内由x和y陀螺引起的导航误差为0。标度因数误差和安装误差经过旋转调制也可降低其对导航系统的影响，但与陀螺漂移和加速度计零偏相比并不显著。

由此可知，旋转调制技术主要是通过在导航系中改变陀螺方向，使在静止和旋转过程中等效陀螺漂移引起的导航误差在一个周期内抵消，从而提高导航精度，传统的单轴双位置转位方案的一个周期旋转步骤如下：

1)停止ts时间长度，正向转动180°；

2)停止ts时间长度，正向转动180°；

3)停止ts时间长度，反向转动180°；

4)停止ts时间长度，反向转动180°。

由于双位置转位方案中转位机构旋转范围在0～360°，需要通过滑环进行旋转，要求转位机构具备滑环。有学者提出了不需要滑环的单轴四位置转位方案，该方案中转位机构的旋转范围为0～270°，其调制效果与双位置转位方案相当。

2 抑制航向运动对调制效果降低作用的转位方案

在载体相对导航系静止的情况下，IMU相对导航系按照既定的规律旋转可将陀螺漂移引起的导航误差抵消。但是在实际中，载体的运动无法保证b系与n系始终重合，在载体航向运动的影响下，IMU若仍按照原规律旋转，陀螺漂移和加速度计零偏引起的导航误差将无法在一个周期内抵消，这会降低旋转调制的效果。

假设初始时刻b系与n系重合，转位机构角度为0，转位机构停止Ts时间长度，期间载体仅做航向运动。定义θ、γ、ψ分别为IMU的俯仰角、横滚角和航向角，设在转位机构停止的时间内IMU的航向角为ψ(t)，则陀螺的等效漂移为：

(7)

其中:

(8)

对式(7)在0～Ts内积分，得到由陀螺漂移在Ts时间长度内引起的姿态角误差为：

(9)

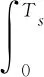
(10)

式(9)与式(10)相加得到0～Ts和t1～t1+Ts两次转位机构停止过程中累计姿态角误差为：

(11)

(12)

式(11)与式(12)相加得0～Ts，t1～t1+Ts，t2～t2+Ts三个时间段内的陀螺漂移引起的姿态角误差为：

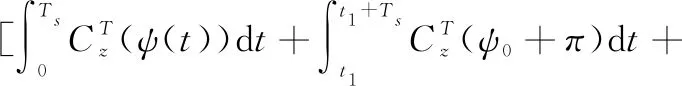
(13)

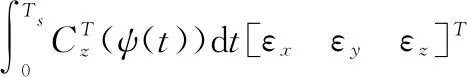
1)停止ts时间长度，正向转动，当|cos(ψ(t))+ic/ts|<σ(σ为一小量，用于判断误差的消除程度，在100 Hz的采样频率下可设置为0.01)且sin(ψ(t))与is异号时停止转位机构；

2)停止ts时间长度，正向转动180°；

3)停止ts时间长度，反向转动，当|sin(ψ(t))+is/ts|<σ且cos(ψ(t))与ic异号时停止转位机构；

4)停止ts时间长度，反向转动180°。

其中，ic和is是cos(ψ(t))和sin(ψ(t))的累加值，转位机构停止过程中ic(n)=ic(n-1)+cos(ψ(tn)),is(n)=is(n-1)+sin(ψ(tn))；而转位机构转动时ic和is值不变。

3 仿真实验

在仅做航向运动的摇摆基座环境下仿真对比无旋转调制、传统双位置旋转调制方案和灵活双位置旋转调制方案的导航误差。

实验步骤：

1)在摇摆基座下，IMU只有姿态角发生变化，导航系速度为零，经纬度不发生变化。通过旋转方案得到IMU在不同时刻的姿态角，由惯导解算算法的逆运算得到陀螺和加速度计的模拟数据；

2)以陀螺和加速度计的输出模型为规律对模拟数据添加零偏、标度因数误差、安装误差和随机游走误差；

3)对添加误差之后的数据进行解算，绘制定位误差曲线并做比较。

假设载体初始状态和误差如表1所示，其中θ、γ和ψ为IMU的俯仰角、横滚角和航向角，vi(i=E,N,U)为载体在东向、北向、天向的初始速度，L、λ和h为载体的纬度、经度和高度，Δx(x=θ,γ,ψ,vE,vN,vU,L,λ,h)为初始状态的测量误差。

表1 初始状态和误差

载体持续做摇摆运动，两种旋转调制方案停止时间均为300 s，旋转角速度均为6°/s。

惯性器件误差参数如表2所示，其中3个陀螺参数相同，3个加速度计参数相同。

表2 惯性器件误差参数

载体仅做航向摇摆运动，在不同的摇摆频率下仿真运行72小时，对比导航结果。

实验1：t时刻天向角速度为ω(t)=6cos[(π/60)t] (°/s)，仿真结果如图2。

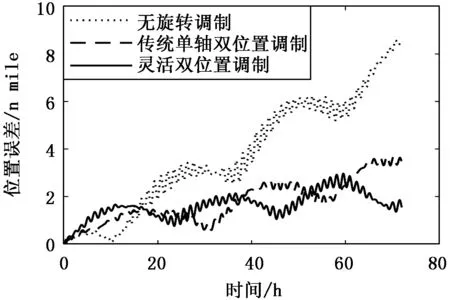
图2 实验一不同调制方案定位误差对比

实验结果显示，无旋转调制的捷联惯导定位误差为8.57 n mile，传统单轴双位置调制方案的定位误差为3.70 n mile，本文设计的灵活双位置调制方案定位误差为2.97 n mile。

实验2：t时刻天向角速度为ω(t)=6cos[(π/30)t] (°/s)，仿真结果如图3。

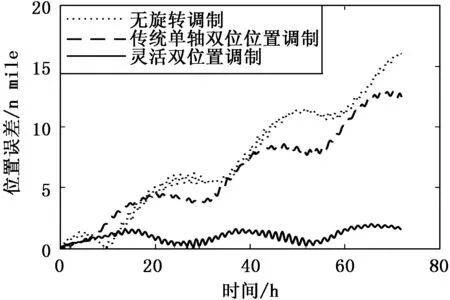
图3 实验二不同调制方案定位误差对比

实验结果显示，无旋转调制的捷联惯导定位误差为16.13 n mile，传统单轴双位置调制方案的定位误差为12.90 n mile，本文设计的灵活双位置调制方案定位误差为1.98 n mile。

仿真结果显示在以上两种条件下，灵活双位置方案误差调制效果均优于无航向运动隔离的传统双位置调制方案。对于实验2，摇摆周期与停止时间相同，传统双位置调制基本失效，但灵活双位置仍显示出较好的调制效果，证明灵活双位置旋转调制方案可在一定程度上抑制航向运动对旋转调制效果的影响。

4 结论

本文分析了航向运动对单轴旋转捷联惯导系统等效陀螺漂移调制效果的影响，设计了一种基于传统双位置转位方案的灵活双位置转位方案，通过仿真实验，说明所设计的转位方案能在不提高转位机构运行频率的条件下有效抑制航向运动对旋转惯导系统调制效果的影响，保证调制效果，提高系统导航定位精度。