绕射波探测浅层空洞的正演模拟与成像初探

张燕生　陆金波

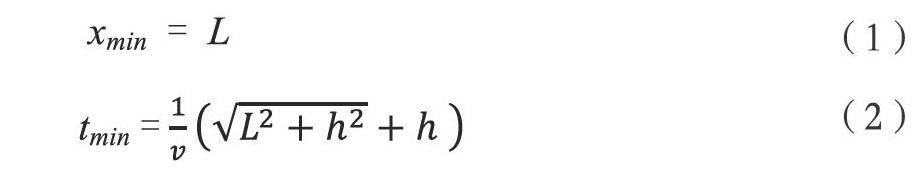
摘 要：利用传统的反射波地震勘探分辨率很难满足小尺度浅层地下空洞的探测需求，地震产生的绕射波却因其特有的传播特性，使得发现浅层地下空间中存在的小尺度异常成为可能。本文通过建立浅层地下空洞地质模型并进行地震波场正演分析，阐明绕射波能够对埋深20 m 至50 m、异常尺度为2 m的空洞进行有效的刻画成像，从而说明，在地下工程（隧道、管线等）建设过程中，可以通过合理布设地震观测系统，运用绕射波地震勘探方法对浅层地下空洞进行较好地探测，提高城市建设的安全性。

关键词：绕射波;空洞异常;浅层勘探;地下空间;地下工程

Abstract： It is difficult to meet the needs of small-scale underground cavity detection for the resolution of the classical reflection seismology. However， diffractions generated from seismic wave propagation procedure would be more properly to detect the small-scale anomalies in the shallow underground space due to their unique propagation characteristics. This paper states that diffractions can effectively imagine the cavity with an abnormal size of 2m in the depth of about 20 m to 50 m， through modeling the near subsurface cavity and forwarding seismic wave. The forward modelling results show that diffraction wave can effectively describe the cavity with an abnormal size of 2 m in the buried depth of 20 m to 50 m. It shows that the diffractions exploration method is much benefit to detect shallow cavity by certain suitable seismic survey system in those city underground engineering （tunnel， pipeline， etc.） projects， even then guarantee the safety of urban construction.

Keywords： diffractions; cavity anomalies; shallow survey; underground space; underground engineering

0 引言

城鎮化进程的加速，促使地下工程（隧道、管道等）建设不断增加。浅层地下空洞（灰岩溶洞、水流冲刷形成的涵洞或地下坍塌等）成为地下工程施工探测中的难点，制约了城市建设施工安全。因此，查明地下空洞分布情况是保障地下工程建设安全的重要任务。传统探地雷达能够有效探测地下3 m 至5 m 的脱空，但对于埋深十几米至几十米以下的空洞或涵洞无法探测。电法勘探探测深度较大，但分辨率差，无法满足对小尺度的空洞探测精度的要求。

浅层反射波地震勘探在城市地质勘查、水利工程勘查及岩土工程勘查工作中逐渐普及（金维民等，2004;蒋维平等，2008;吴怡等，2006），该方法震源能量小，对周围环境无明显破坏，同时勘探精度相对较高。但随着工程勘探精度要求的提高，想要辨识灰岩地层中2m尺度的空洞，利用浅层地震勘探很难获得较好的探测效果。从地震勘探理论出发，地震勘探纵向上分辨率为1/4波长。要识别2 m异常，则要求波长不能低于8 m，灰岩溶洞的地层速度以2400 m/s计算，则地震勘探的主频需达到300 Hz以上，该频率在现阶段反射波地震勘探中难以实现。对于横向分辨率而言，要识别2 m尺度的异常，亦极为困难。

地震波在经过地下小尺度断层、尖灭或孔洞时，会产生绕射波。绕射波在地震波场中与反射波具有特征差异，绕射波具有超分辨率能力，即绕射波能够识别小于地震波长异常体的能力。地质勘查领域中地震技术应用不断深入，绕射波的作用不断得到重视（Khaidukove et al.，2004;Bansal et al.，2005;Moser et al.，2008），物理模型和波场计算方面成果显著。同时，绕射波成像技术也得到较好的发展（李正伟等，2018;黄建平等，2012;刘玉金等，2013），进一步推动了绕射波在地震勘探中的应用。本文在前人对绕射波理论研究的基础上，对溶洞或其他地下空洞发育的地质模型进行地震波场正演，分析绕射波在相应地质特征下对浅层空洞的识别能力。

1 绕射波勘探原理

地震波在地层中传播时，遇到小尺度（小于波长）异常体或岩性突变点，这些异常点会成为新的震源，发出子波向周围传播。这些新产生的波成为地震绕射波（陆基孟等，2011）。以断棱产生的绕射波为例说明绕射波与反射波的时距曲线差异。

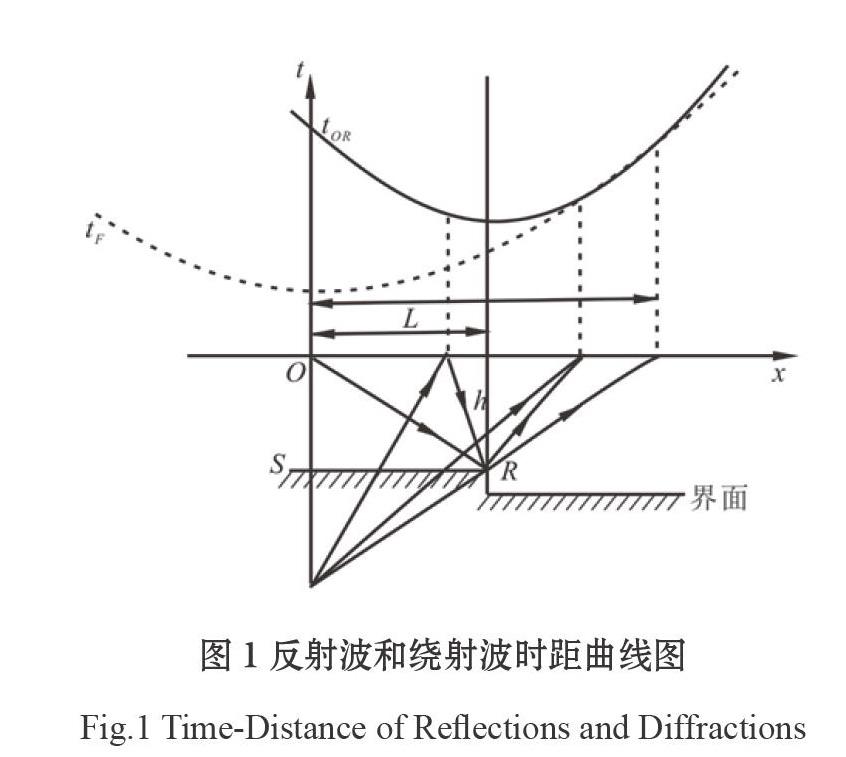
图1中反射界面S中间发育断棱R，地震波传播到R点处出现绕射波。测线OX与断棱垂直，激发点位于O点。地震波从O点发出，传播到R点后，以R点为中心（R点为虚震源）产生绕射波，被测线上个接收道接收。其中虚线为tF为O点震源激发，反射界面RS的反射波时距曲线;tR为O点激发R点产生绕射波的时距曲线。推导过程在文献中有详细说明。绕射波的时距曲线也可以变换为标准双曲线方程。当测线与断棱垂直的情况下，绕射波时距曲线的极小点xmin位于绕射点的正上方，其对应的极小时间tmin，即：

激发点移动时，绕射波的时距曲线极小点在测线上的位置不变，但时距曲线会沿t轴平移，时距曲线的形态保持不变。利用绕射波时距曲线的这些特点在共炮点地震记录中能够较好的识别绕射波。

2 理想地质模型中绕射波特征分析

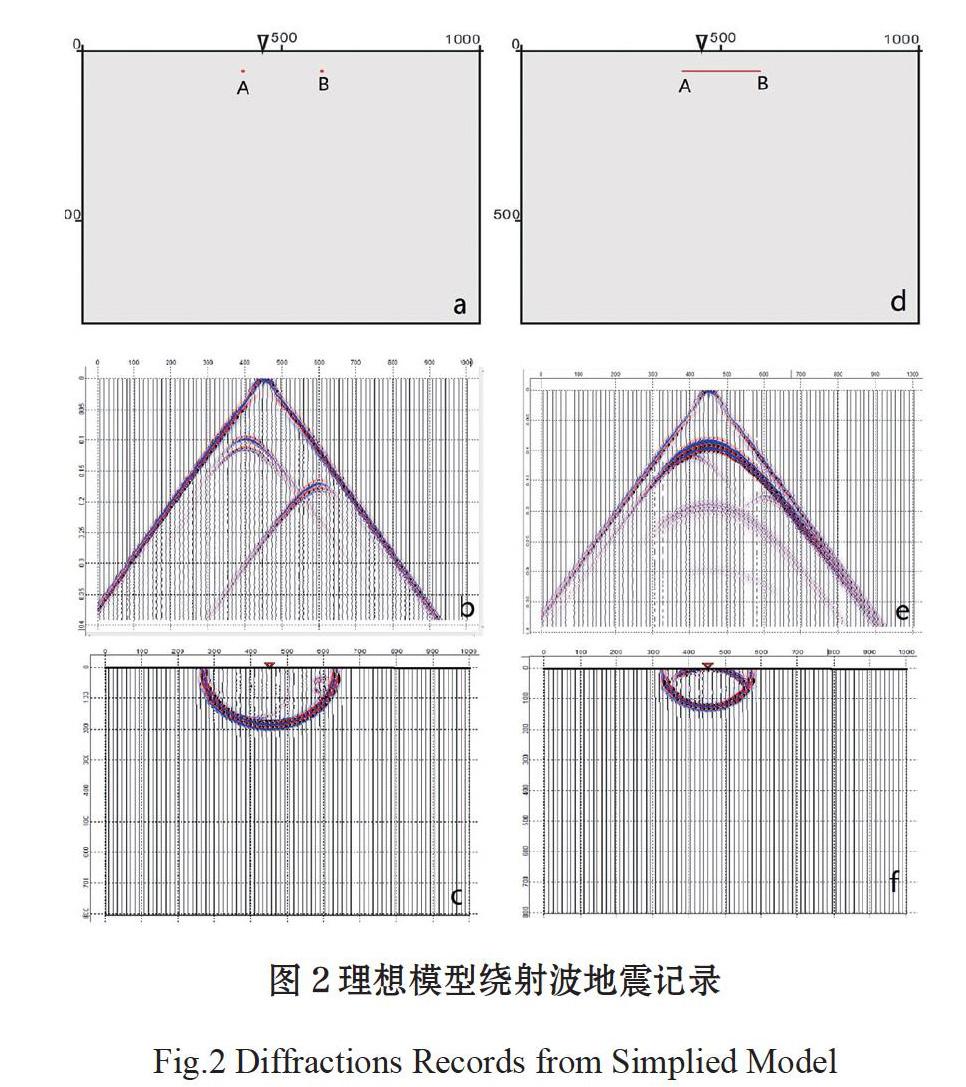
为了能够识别地层中绕射波地震记录特征，我们建立了两个理想的地质模型。模型1如图2a所示，为水平地表，均质地层，长度1000 m，深度800 m，纵波速度1200 m/s，内部未设计反射界面，震源位置（450，0）点，检波点位于地表，间隔距离2 m，在A点（400，60）和B点（600，60）两点设置绕射点，模型中绕射点的尺度设置为2 m。用主频100 Hz的雷克子波进行正演模拟，介质中地震波长12 m，远大于绕射点尺度。图2b是模型1的共炮点道集，道集上显示3组地震波，分别为直达波和两个绕射点产生的绕射波。图中可见绕射波极小点对应地表投影与绕射点对应地表投影位置一致。但两组绕射波极小点对应的时间不一致，反映出A、B两点相对震源距离的差异，正如绕射原理所描述，震源相对位置的改变，不改变绕射波组的极小点的位置，只是绕射时距曲线在t轴上移动。由于模型中未设计反射面，同时绕射点尺度远小于地震波长，不足以产生反射波，因此，正演道集中没有反射波显示。该理想状态下的地质模型，能够清晰的展示绕射波在共炮点道集下的波组特征，为灰岩溶洞绕射波识别提供模式基础。图2c展示的是绕射波产生的波场特征。地震波自震源产生，以球面形式向外扩张，捕获图2c的时刻波面已经通过绕射点，以绕射点为中心在波后产生向周围扩散的绕射波。

模型2如图2d所示，在模型1的同尺度水平地表地质模型中，将模型1中A、B两个绕射点进行连线，设置成为一个反射界面，模拟一个理想状态下不连续沉积的地质模型。根据绕射波产生的条件在该反射界面A、B两端将产生绕射波。用主频100 Hz的子波对模型进行正演，震源位置与模型1等同。对该模型进行正演，图2e为正演的共炮点地震道集。可见，直达波，AB界面反射波、A、B两个端点产生的绕射波以及层间多次波（干扰波）。绕射与反射波组部分重合，仍可觀察到两套绕射波组的极小点位置，该位置与模型1两个绕射点的位置一致。图2f为该模型正演的波场快照，绕射波以不连续地层断点为中心向周围扩散。因此，在单纯绕射点地质模型或不连续地层模型中，在炮集上或波场特征上，绕射波与反射波有明显差异，利用叠前的处理手段在去除多次波的基础上，采取有效的绕射波分离方法，即可将反射波去除，获得如模型1一致的绕射剖面，进一步获得绕射波成像数据。

3 灰岩溶洞地质模型正演

结合灰岩地层发育特征，建立灰岩溶洞地质模型。以武汉地区为例，灰岩地层一般埋深20～50 m，灰岩中纵波速度4500 m/s，上覆地层纵波速度1200 m/s。设计模型长1000 m，深度600 m。灰岩与上覆低速层界面深度50 m，在x=350 m和x=600 m处设计两个溶洞，溶洞尺度分别为5 m和2 m。溶洞位地层界面下3 m处，内部充满水。

观测系统设置。本次正演过程中采用中间放炮，两边接受方式。设置51炮，间隔10 m，均匀分布在x=250 m至x=750之间。检波点设置：间隔2 m，最大偏移距100 m，滚动排列。

研究过程中采用Tesseral 2D全波场正演模拟软件，该软件基于射线追踪和有限差分标量波动方程的简化算法，能速有效的对复杂地质模型开展正演计算。

正演过程中采用主频100 Hz雷克子波，对灰岩溶洞地质模型进行正演（图3）。正演炮集上能够清晰观测到两个溶洞产的绕射波（图4），说明该地质特征上，能够利用绕射波对灰岩溶洞进行识别工作。但绕射波能量弱、衰减快，难以在强反射波场中显示出来，因此，在数据域内进行绕射波信息分离，对绕射波信息进行偏移成像，有助于地质工作者，对灰岩溶洞进行有效刻画。

4 效果分析

在岩溶地质模型波场正演模拟的基础上，对道集数据进行偏移成像。在不进行绕射波分离工作情况下，进行传统的偏移成像，成像结果如图5a，可见清晰灰岩顶界面反射波组，但溶洞在偏移剖面上没有反应。如前所述，正演设计中，主频100 Hz的子波，在v1=1200 m/s和v2=4500 m/s的地层中波长分别为λ1=12 m和λ2=45 m，岩溶尺度（2 m、5 m）小于波长，难以产生有效反射，导致反射波偏移剖面中，岩溶体不可见;在绕射波分离基础上，对绕射波进行分离成像，成像结果如图5b。在x=350 m和x=600 m位置下清晰可见岩溶体产生的波组响应。左侧波组能量比右侧波组能量强，说明岩溶异常体的尺度对波场中产生绕射波的强度有影响，解释过程中，通过模型分析，能够建立岩溶体相对尺度关系。

正演试验过程中对子波的主频进行替换，结果显示在理想状态下（不考虑地震波频散、高频衰减、层间多次波），地震勘探采用频率越高，绕射波对小尺度岩溶异常体的刻画能力越好，见图6。但实际勘探过程中，地震频散、高频衰减、多次波以及检波器采样能力等客观因素都会对绕射波勘探造成影响。因此，在勘探过程中，需进一步结合实际地质情况，选取合适的观察系统以及震源、检波器等，来保证接受数据中获取有效的绕射波信息。

国内外众多学者对绕射波的分离与成像有长期大量研究。Landa等（1987）利用相位校正方法，对绕射波在共偏移距剖面上进行目标定位;Nowak等（2004）通过比较波场中绕射波和反射波时距曲线在极小点位置差异，对其曲线进行拉东变换，实现绕射波提取工作;Berkovitch等（2009）利用局部时差校正方程将绕射波时差曲线进行参数化，从而获取高信噪比绕射波叠加剖面;Asgedom等（2011）修正传统共反射面元叠加方基础上，结合相似度分析和多信号分类技术，将绕射波从波场中分离。赵惊涛等（2011）指出共偏移距剖面中振幅主能量及极性反转出现在绕射点的地面投影处，因此，共偏移距剖面更有利于绕射波的识别与分离。近年来基于反稳相滤波绕射成像技术（刘培君等，2017）、最小二乘自适应滤波的绕射波分析技术（李学良等，2013）不断出现，绕射波分离与成像技术日趋成熟。

根據绕射波分离过程在整个地震数据处理流程中的阶段，总体可分为叠前绕射波分离和叠后绕射波分离。叠前绕射波分离依据绕射波和反射波的波场走时规律及特征差异，相位特征差异，能量特征差异等因素，在成像算子中进行分离成像;叠后绕射波分离成像主要包括优势倾角滤波法、PWD法（Plane Wave Decomposition，平面波分解）、奇异值分解方法等。

本次绕射波偏移基于kirchhoff积分偏移理论，如下：

这里P（xs， xr， z=0）为地表观测得到的波场值，p（x， z， t）为反射点（x， z） 处在t时刻的波场值，rs和rr分别代表炮点到反射点、检波点到反射点的距离，vd和vu分别代表下行波和上行波沿射线路径的均方根速度或层速度，系数A为保幅处理因子，作为振幅比例因子，实现保幅处理。

5 结论

灰岩岩溶地质条件给地下空间建设施工带来巨大安全隐患，常规物探方法难以有效的探测到埋深较大的岩溶异常。相对于传统反射波地震勘探，在提高线道密度的基础上，利用地震绕射波超分辨率能力，对分离的绕射波进行偏移成像，能够对灰岩地层中岩溶异常体进行有效的刻画。正演结果表明，对于埋深50 m，尺度2 m的溶洞，在道集数据上能够识别到清晰的绕射波，绕射波偏移剖面上，波组能够正常归位，显现岩溶体发育空间位置。同时，正演显示岩溶体尺度对绕射波能量相关，尺度相对大的岩溶体产生的绕射波能力相对小尺度的岩溶体产生绕射波的能量强，通过这一相对关系，在岩溶体刻画过程中，根据波组能量关系可以相对获取岩溶体的相对尺度。总之，在深埋溶洞探测方面，绕射波地震勘探具有切实意义，随着地震采样能力的提高以及处理手段的不断改善，绕射波对灰岩地层小尺度岩溶刻画能力会不断提高。

参考文献：

黄建平， 李振春， 孔雪， 等， 2012. 基于PWD的绕射波波场分离成像方法综述[J]. 地球物理学进展，27（6）：2499-2510.

金维民， 杜兵建， 2004. 浅层地震勘探在滑坡勘查中应用[J]. 中国煤田地质（S1）：97-99.

蒋维平， 孟宪民， 2008.地震反射波法在浅层勘探中的应用[J]. 中国煤炭地质（9）：59-60+67.

陆基孟，王永刚，2011. 地震勘探原理[M]. 3版.北京：中国石油大学出版社.

李正伟， 张剑锋， 刘伟， 2018. 基于倾角-偏移距域道集的绕射波成像[J]. 地球物理学报，61（4）：1447-1459.

刘培君， 黄建平， 李振春， 等， 2017. 一种基于反稳相的深度域绕射波分离成像方法[J]. 石油地球物理勘探， 52（5）：967-973+879.

刘玉金， 李振春， 黄建平， 等， 2013. 绕射波叠前时间偏移速度分析及成像[J]. 地球物理学进展，28（6）： 3022-3029.

李学良， 孙晨， 袁义明， 等， 2013. 利用最小二乘自适应滤波实现绕射波分离[J]. 地球物理学进展，28（2）：777-784.

吴怡， 嘉世旭， 段永红， 等， 2006.地震折射波法在郑州市西区浅层勘探中的应用[J]. 地震地质（1）：84-92.

赵惊涛， 王真理， 于彩霞， 2011. 地震勘探中的边缘绕射波及其动力学识别方法[J]. 地球物理学进展，26（1）：194-206.

Asgedom E G， Gelius L J， Austeng A， et al.， 2011. A new approach to post-stack diffraction separation[R]. SEG Expanded Abstracts， 3861-3865.

Bansal R， Imhof M G， 2005， Diffraction enhancement in prestack seismic data[J]. Geophysics， 70（3）：73-79.

Berkovitch A， Belfer I， Hassin Y， et al.， 2009. Diffraction imaging by multifocusing[J]. Geophysics， 74（6）：75-81.

Khaidukov V， Landa E， Moser T， 2004， Diffraction imaging by focusing-defocusing： An outlook on seismic superresolution[J]. Geophysics， 69（6）：1478-1490.

Landa E， Shtivelman V， Gelchinsky B， 1987. A method for detection of diffracted waves on common-offset sections[J]. Geophysical Prospecting， 35（4）：359-373.

Moser T， Howard B C， 2008. Diffraction imaging in depth[J]. Geophysical Prospecting， 56（5）：627-641.

Nowak E J， 2004. Diffractor localization via weighted Radon transforms[J]. SEG Technical Program Expanded Abstracts， 23（1）：2586.