不同工况条件对均质土体稳定性的影响
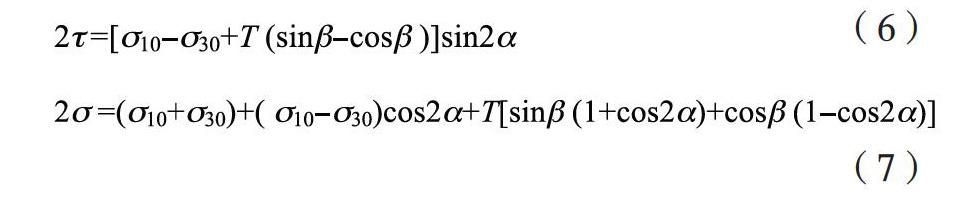
摘 要:土体破坏的主要表现形式是剪切破坏,土体抵抗破坏的能力(强度)主要表现为内聚力和内摩擦力。土体的稳定性则表现为土体薄弱面上的剪应力及抗剪强度之间的相互关系:当薄弱面所受的剪应力大于抗剪强度时,土体丧失稳定性,从而发生破坏;当薄弱面所受的剪应力小于抗剪强度时,土体保持稳定。在滑坡治理或保持基坑稳定的措施中,修建挡土墙、抗滑桩,加固基坑土体被动区、坡顶卸载、施加锚杆以及修建排水设施是常见的手段。不同治理工程措施构成不同工况,或改变了土体的应力状态,或增加了土体的强度,从而使边坡土体的稳定性得到提高。考察土体内某个截面,首先按照土力学原理判断求出该面上的正应力σ与剪应力τ的变化,然后根据土体强度理论判断出该面上的抗剪强度τf的变化,进而可以根据剪应力τ与抗剪强度τf的关系判断出土体是否趋于稳定或者不稳定。
关键词:剪应力;抗剪强度;应力状态;工况;土体稳定性
Abstract: The soil mass failure mainly shows the shear failure form, and its strength of anti-failure is mainly related to cohesion and friction. The stability of soil mass is to study the relationship between the shear stress and shear strength on the weak surface of soil mass: when the shear stress on the surface is greater than the shear strength, the soil mass will be damaged; when the shear stress on the surface is less than the shear strength, the soil mass will remain stable. In the measures of landslide control or maintaining the stability of foundation pit, it is common to build retaining wall, anti-slide pile, strengthen the passive area of foundation pit soil, unload the slope top, apply anchor rod and build drainage facilities. In different treatment projects, the stress state of soil changes correspondingly. On a fixed surface of soil, the change of normal stress (σ) and shear stress (τ) on the surface is determined by mathematical derivation or graphic method, and then the change of shear strength (τf) on the surface is determined by the change of normal stress (σ) and the shear formula of soil, and then the stability or instability of soil mass can be determined by the relationship between τ and τf.
Keywords: shear stress; shear strength; stress state; working condition; stability of soil mass
0 引言
土體是一种碎散的颗粒材料,土颗粒物质的主要成分是各种矿物,具有较大的强度,不易发生破坏。土颗粒之间的接触界面相对软弱,容易发生相对滑移。因此,土体的强度主要由土颗粒间的相互作用力决定,而不是由土颗粒的强度决定。这个特点决定了土体破坏的主
要表现形式是剪切破坏,符合莫尔强度理论,其强度主要表现为内聚力和内摩擦力(李广信等,2013)。土体强度指标可通过试验测定,室内试验常用的方法有直接剪切试验、三轴压缩试验、无侧限抗压强度试验等;原位试验常用的方法有平板载荷试验、十字板剪切试验、现场直剪试验、旁压试验等(工程地质手册编委会,2018)。在土体工程中,为改善土体的稳定性,采用不同的治理工程措施,从而构成土体的不同工况,或改变了土体的应力状态,或增加了土体的强度,从而使边坡土体的稳定性得到提高。本文从不同工况条件对土体应力和强度的作用入手,研究土体内破坏面上的应力状态和土体强度的改变,进而探讨土体的稳定性的变化过程。
1 不同工况土体的应力状态
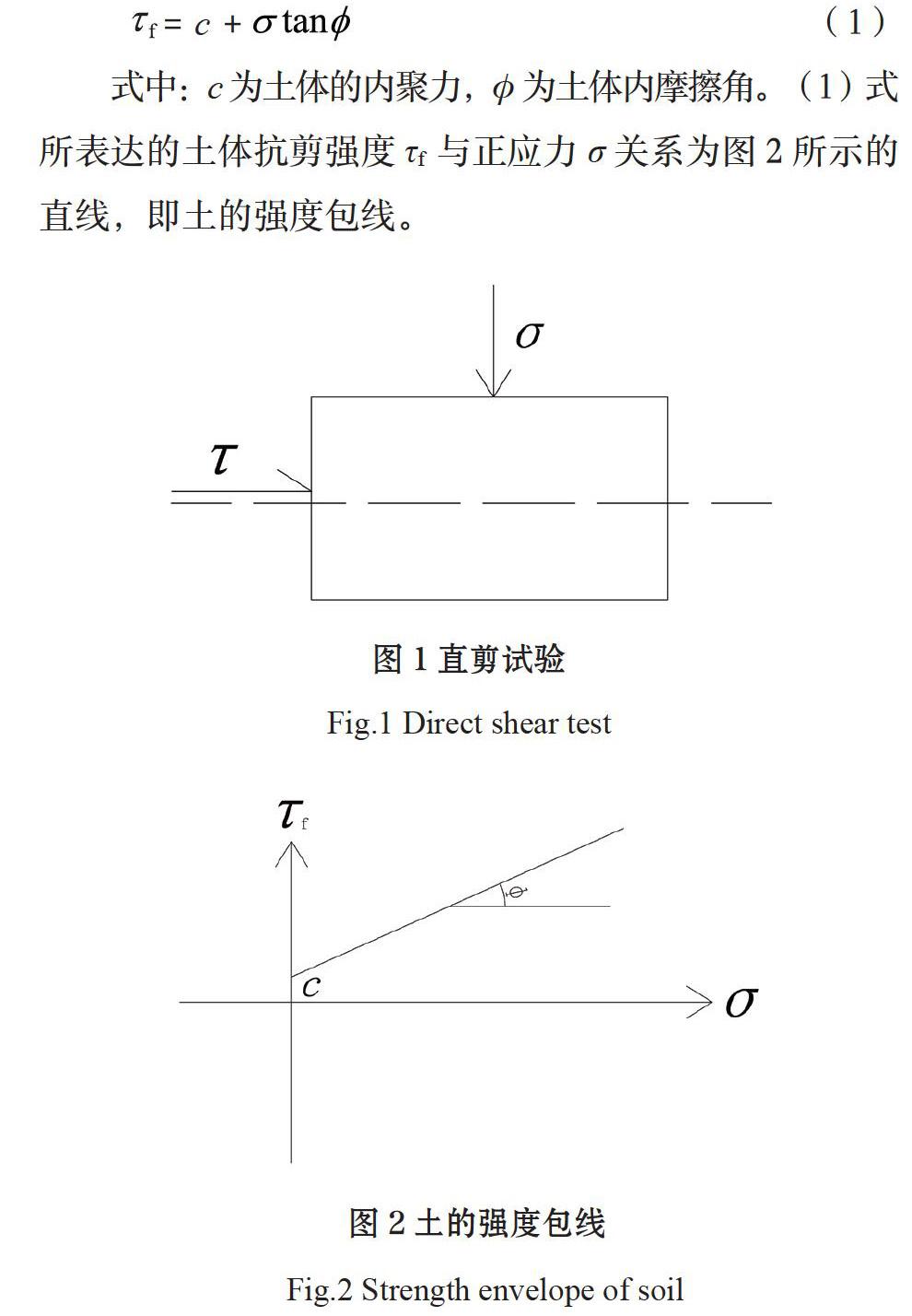
按照莫尔强度理论,土体的稳定性取决于土体薄弱面上的剪应力及抗剪强度之间的相互关系。当薄弱面所受的剪应力大于抗剪强度时,土体发生失稳破坏;当薄弱面所受的剪应力小于抗剪强度时,土体保持稳定。如图1所示,由直剪试验可以直观看出剪切面上的剪应力τ与抗剪强度τf二者的关系。
首先对试样施加竖向压力P,然后对可以移动的下盒施加水平推力T。刚开始水平力T较小,试样在上、下盒间的受剪面未发生位移,作用在土样受剪面上的剪应力为τ=T/A、正应力为σ=P/A,其中A为土样的受剪面积。随着水平力T不断增大,当T增大到一定值时,土体发生破坏,此时土体所受的剪应力τ等于抗剪强度τf。此过程中:当τ﹤τf时,土样未发生破坏;当τ=τf时,土样达到极限平衡状态;当τ>τf时,土样即发生破坏。
对于土体的抗剪强度τf随剪切面上的法向应力σ的增加而增大,抗剪强度随法向应力的变化规律符合式(1)所示的莫尔强度理论:
式中:c为土体的内聚力,φ为土体内摩擦角。(1)式所表达的土体抗剪强度τf与正应力σ关系为图2所示的直线,即土的强度包线。
直剪试验操作方便,土样的受力状态较为简单,土样的破坏直观可见。但是原位状态的土体破坏面一般并不是像直剪试验那样是事先控制的,应力状态的空间分布也较为复杂。一般,原位土体处于三维应力状态,即大主应力σ1,中主应力σ2,小主應力σ3,根据莫尔库仑强度理论,中主应力σ2对土强度的影响不大,在工程上一般不考虑,所以土工实验室常做的常规三轴实验是用围压作为土样的最小主应力σ3,在土样轴向施加竖向荷载形成最大主应力σ1>σ3,从而土样受到的偏差应力 (σ1-σ3) 在土样中形成最大剪应力τmax=(σ1-σ3)/2。常规三轴试验中土样所处的应力状态如图3所示。
在图3中,土体中与最小主应力σ3方向夹角为α的截面(或者说,法线方向与最大主应力σ1方向夹角为α的截面,简称截面α)上的正应力σ和剪应力τ 随着作用面的转动(夹角α变化)而发生变化,可以用图4所示莫尔圆代表土样内平面α上的应力状态,莫尔圆上一个点对应的正应力σ、剪应力τ就是作用在平面α上的正应力σ、剪应力τ。
对图3所示的土样应力状态,在土体内截面α上的法向应力σ与剪切力τ与主应力σ1、σ3的关系如式(2)所示:
式中:α为截面与最大主应力σ1作用面的夹角(或者说,截面法线方向与最大主应力方向之间的夹角)。可以证明,式(2)就是σ-τ坐标系中半径为 (σ1-σ3)/2、中心在 [(σ1+σ3)/2, 0]的圆,称为应力莫尔圆。莫尔圆周点沿圆周的转动方向和平面α转动方向相同,但其转角大小是截面α转角的2倍(松岗元,2001)。截面α上的正应力σ和剪应力τ随着作用面的转动(夹角α变化)而发生变化,可以用图4所示莫尔圆代表土样内平面α上的应力状态,莫尔圆上与σ呈2α上的点对应的正应力σ、剪应力τ就是作用在截面α上的正应力σ、剪应力τ。
如图5所示,按照莫尔强度理论,当应力莫尔圆与土体强度包线相切时,土体沿切点对应的截面α发生剪切破坏。
如果可能发生剪切破坏面的位置已经预先确定,只要知道作用于该面上的剪应力和正应力,就可以判别剪切破坏是否发生。对于均质土体,在最小主应力σ3一定的情况下,随着最大主应力σ1的增大,莫尔圆半径 (σ1-σ3)/2也随之增大。当应力莫尔圆与土体强度包线相切时,土体发生破坏。根据几何关系,可知α=45°+φ/2,即破坏面与大主应力作用面呈45°+φ/2的夹角。可见,土体的最易破坏面并不是土体所受到的最大剪应力面(与大主应力作用面呈45°夹角的面,如图5所示应力莫尔圆中的A点),因为该面上τ﹤τf。剪切破坏面位置一经确定,只要知道作用于该面上的剪应力和正应力,就可以根据土体的强度包线与最易破坏面(截面α=45°+φ/2)上剪应力与抗剪强度的关系判别剪切破坏是否发生。
一般情况下,受土压力推动(主动土压力)挡土结构会发生离开填土方向的移动,此时墙后土体应力状态的最大主应力σ1为铅锤向的自重应力,最小主应力σ3沿水平方向作用。在滑坡治理或基坑支护措施中,修建挡土墙、抗滑桩,加固基坑土体被动区、坡顶卸载、施加锚杆以及修建排水设施是常见的手段。其中修建挡土墙、抗滑桩,加固基坑土体被动区可以简化为对土体施加了额外的水平侧向压力,使土体中水平方向的最小主应力σ3加大;坡顶卸载可以简化为减小了铅锤向的最大主应力σ1;施加锚杆可以简化为增加了土体内部沿锚杆方向的轴向力(σ1、σ3均增大);修建排水设施阻止水体渗入土体,相当于阻止了土体内部软弱面上正应力σ(土体颗粒间有效应力)的减小,从而避免了土体强度的降低。
采用数学分析或图形判断方法,考虑土体上述应力状态的变化,分析土体内截面α(特别是最易破坏面α=45°+φ/2)上剪应力τ与正应力σ的变化,进而比较剪应力τ与抗剪强度τf的关系,从而对土体稳定性做出判断。
2 不同工况土体稳定性的判断
2.1 侧向应力变化
修建挡土墙、抗滑桩,加固基坑土体被动区可以看作是对土施加了额外的侧向力(侧向加荷)。简化后的应力状态为最大主应力σ1不变,最小主应力σ3增大;相反,拆除围挡结构、坡脚卸载可以看作是减小了土体的侧向力(侧向卸荷)。
(1)数学分析法
对于土体内截面α(0﹤α﹤90°)上的剪应力τ,按式(2)中的第二式计算:
若σ1不变,当σ3增大时,剪应力τ变小;σ3减小时,剪应力τ变大。
对于土体内截面α(0﹤α﹤90°)上的正应力σ,按式(2)中的第一式计算:
若σ1不变,当σ3增大时,σ变大;σ3减小时,σ也变小。
按莫尔强度表达式 ,同一位置土体的强度参数c、φ 值不变,σ1固定不变。则随着σ3增大,截面α上的法向应力σ随之变大,对应的土体抗剪强度τf也随之变大,但沿截面α方向的剪应力τ逐渐减小,土体稳定性得到加强;相反,若σ3逐渐减小,则截面α上的法向应力σ也随之减小,从而导致对应的土体抗剪强度τf降低,但沿截面α方向上的剪应力τ逐渐变大,土体稳定性受到削弱。
(2)图形判断法
由图6、图7可见,土体强度参数c、φ值一定,强度包线不变。修建挡土墙、抗滑桩,加固基坑土体被动区改变了边坡土体的应力状态,相当于最大主应力σ1不变,最小主应力σ3增大(修筑挡土墙等)或减小(拆除挡土墙等)。土体应力状态变化也会反映到应力莫尔圆上,并使莫尔圆与土体强度包线的关系发生变化。根据这些变化,可以对土体稳定性的变化做出判断。
如图6所示,修筑挡土墙等情况下最大主应力σ1不变,最小主应力σ3逐渐增加。随着σ3增大,应力莫尔圆圆心[(σ1+σ3)/2, 0] 不断向右移动,莫尔应力圆的半径 (σ1-σ3)/2越来越小,且应力莫尔圆越来越远离强度包线,发生τ≥τf的可能性越来越小,说明土体趋向于稳定。
相反,如图7所示,拆除挡土墙等情况下最大主应力σ1不变,最小主应力σ3逐渐减小。随着σ3减小,应力莫尔圆圆心[(σ1+σ3)/2, 0] 不断向左移动,莫尔应力圆的半径 (σ1-σ3)/2也越来越大,且应力莫尔圆越来越靠近强度包线,土体内最易破坏面(α=45°+φ/2)上的剪应力τ逐渐向土体的抗剪强度τf逼近,说明土体趋向于不稳定。当应力莫尔圆与强度包线相切时,土体内最易破坏面上τ=τf,土体破坏。
2.2 竖向应力变化
坡顶堆土,停放机械设备可以看作是增大了土的竖向应力,简化后的应力状态为最大主应力σ1变大,最小主应力σ3不变。相反,坡顶卸载可以看作是减小了土的竖向应力,简化后的应力状态为大主应力σ1变小,小主应力σ3不变。
(1)数学分析法
按式(2)中的第二式分析,当σ3固定不变时,土体截面α (0﹤α﹤90°)上的剪应力τ与σ1的变化呈正相关,即,σ1变大τ随之变大,σ1变小τ也随之变小。
按式(2)中的第一式分析,当σ3固定不变时,土体截面α(0﹤α﹤90°)上的正应力σ同样与σ1的变化呈正相关,即,σ 隨σ1的增加而变大,随σ1的减小而减小。
按土体强度包线 分析,对于强度参数c、φ值一定的土体,土体的抗剪强度τf与σ的变化也呈正相关。根据上述分析,当σ3固定时σ的变化与σ1的变化呈正相关,进而可推知,土体截面α的抗剪强度τf也与σ1呈正相关,即,τf随σ1变大而变大,随σ1的减小而减小。
根据上述分析,土体内截面α上的剪应力τ和抗剪强度τf均与σ1呈正相关,若要确定τ与τf相对关系的变化趋势(τ<τf,τ=τf,τ>τf),还需要进一步比较τ与τf的变化幅度,这样才能进一步对土体稳定性的变化趋势做出判断。
考虑σ3固定不变,σ1变化在截面α上产生的剪应力变化Δτf和抗剪强度变化Δτ,分别由式(1)和式(2)的第二式可得:
考察最易破裂面(α=45°+φ/2)面上的剪应力τ与抗剪强度τf的变化情况:
由于最易破裂面α=45°+φ/2>45°,所以sinα>cosα。一般,土体的 φ < 45°,所以tanφ<1,sinα>cosα tanφ,从而有 Δτ-Δτf>0,即,σ3固定不变时,对应σ1的变化增量Δσ1,在最易破裂面上,剪应力变化的增量Δτ大于抗剪强度变化的增量Δτf。因此,随着最大主应力σ1的增大,最易破坏面上的剪应力与抗剪强度的关系趋向于τ>τf,即,土体趋向于不稳定;反之,随着最大主应力σ1的减小,最易破坏面上的剪应力与抗剪强度的关系趋向于τ<τf,即,土体趋向于稳定。
(2)图形判断法
由图8、图9可见,土体强度参数c、φ值一定,强度包线不变。坡顶加载、卸载改变了边坡土体的应力状态,相当于最小主应力σ3不变,最大主应力σ1增大(坡顶加载)或减小(坡顶卸载)。土体应力状态变化也会反映到应力莫尔圆上,并使莫尔圆与土体强度包线的关系发生变化。根据这些变化,可以对土体稳定性的变化做出判断。
如图8所示,坡顶堆载等情况下最小主应力σ3不变,最大主应力σ1逐渐增加。随着σ1增大,应力莫尔圆圆心[(σ1+σ3)/2, 0] 不断向右移动,莫尔应力圆的半径 (σ1-σ3)/2越来越大,且应力莫尔圆越来越靠近强度包线,说明土体趋向于不稳定。当应力莫尔圆与强度包线相切时,土体内最易破坏面上τ=τf,土体破坏。
相反,如图9所示,坡顶卸载等情况下最小主应力σ3不变,最大主应力σ1逐渐减小。随着σ1减小,应力莫尔圆圆心[(σ1+σ3)/2, 0] 不断向左移动,莫尔应力圆的半径 (σ1-σ3)/2也越来越小,且应力莫尔圆越来越远离强度包线,说明土体趋向于稳定。
2.3 锚杆加固
边坡土体锚杆加固相当于在边坡土体表面和锚固段(土体内部距离土体表面一定深度)之间的土体受到了沿锚杆方向的压力,可以简化为增加了沿锚杆方向土体内部的压应力。如图10所示,锚杆的倾角β一般为10°~35°,锚杆对土体施加沿锚杆轴向的锚固力(压应力)T(量纲与应力相同)。将锚固力T分解到土体自重应力的最大主应力σ10和最小主应力σ30方向并与相应方向的应力叠加,叠加后的最大主应力增加为σ10+Tsinβ,最小主应力增加为σ30+Tcosβ。因为β在10°~35°之间,所以sinβ﹤cosβ,即,锚杆加固后土体的最大主应力σ1变大的程度小于最小主应力σ3变大的程度。考虑上述锚杆加固后土体的应力状态变化,根据莫尔强度理论,可采用数学分析和图形判断两种方法,对土体的稳定性变化进行预判。
(1)数学分析法
考虑锚杆加固土体内截面α(0﹤α﹤90°)上的剪应力τ和正应力σ,将锚固土体的最大主应力σ1=σ10+Tsinβ和最小主应力σ3=σ30+Tcosβ代入式(2)整理得:
按式(6)分析,由于sinβ﹤cosβ,所以,锚固使土体中截面α上的剪应力τ变小。
按式(7)分析,由于1-cos2α≥1,所以,锚固使正应力σ变大,根据τf=c+σtanφ ,对强度参数(c、φ值)一定的土体,土体截面α的抗剪强度τf也随之增大。
由上述分析可知,在土体截面α上,一方面剪应力τ减小,另一方面抗剪强度τf增大,说明土体锚固使得边坡土体趋向于稳定。
(2)图形判断法
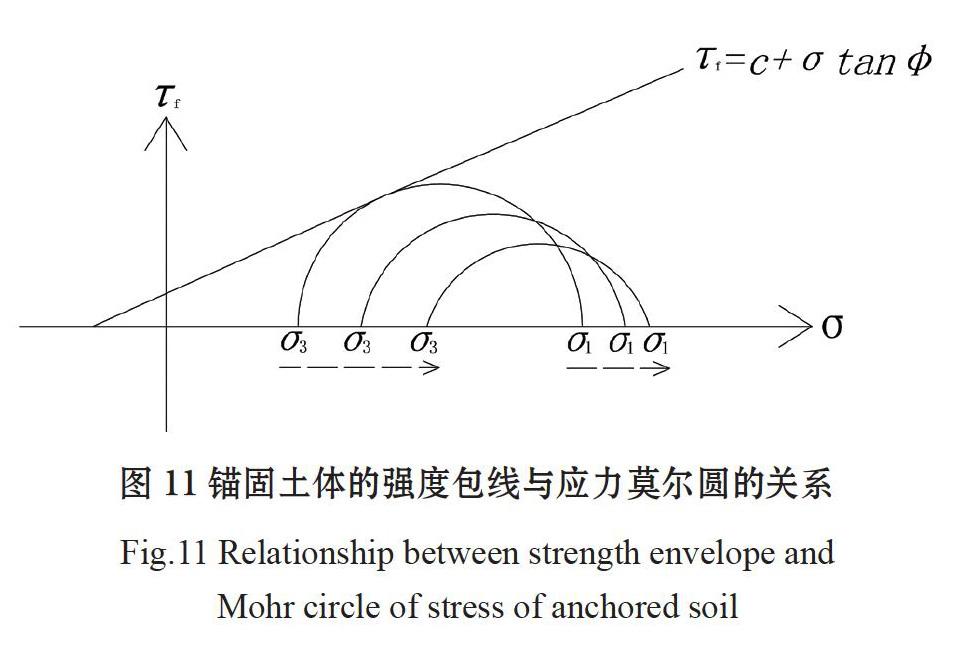
施加锚杆改变了边坡土体的应力状态,根据施加锚固力T后土体最大主应力σ1=σ10+Tsinβ、最小主应力σ3=σ30+Tcosβ的变化可知:锚杆加固后土体最大主应力σ1、最小主应力σ3均变大,但σ1变大的程度小于σ3变大的程度,所以,应力圆在半径减小的同时,圆心也向右移动。如图11所示,在土体强度参数(c、φ值)一定时,土体的强度包线保持不变,而应力莫尔圆越来越小,且离开强度包线越来越远,即土体越来越稳定。
2.4 静水的影响
处在静水环境中(一定深度水体之下,或者潜水面之下)土体最为显著的特点就是孔隙水压力u的存在。静水对土体稳定性的影响分析的主要理论基础是有效应力原理。有效应力原理核心内容主要两个方面:(1)土体内任意截面上的总应力σ可分为土骨架承受的有效应力σ 和孔隙水所承受的孔隙水压力u两部分,即σ=σ +u;(2)土体的变形与强度只取决于有效应力σ ,孔隙水压力u自身的变化并不会使土体的抗剪强度发生变化。土体稳定性分析主要是土体内最易破坏截面α(α=45°+φ/2)上的土体应力与土体强度的比较。
对于静水中土体的抗剪强度,按库伦莫尔强度理论和有效应力原理,静水环境中土体的抗剪强度可表达为如下形式:
以上表达式中,c 、φ 称为土体有效应力抗剪强度参数(强度指标),u为孔隙水压力。
对于静水中的土体的应力状态,可以取土-水整体作为隔离体进行研究,静水作用对隔离体增加了围压,使饱和土体产生了孔隙水压力。此时土体的大主应力增加为:σ1+σu,小主应力增加为σ3+σu,并由此可以计算静水中土体某一固定面上有效应力强度状态下剪应力τ 、正应力σ 、抗剪强度τf (高大钊,2010)。根据有效应力抗剪强度进行土体稳定性分析称为有效应力法。根据有效应力原理,真正对土体抗剪强度有影响的是有效应力,只有有效应力抗剪强度才能确切表达土体抗剪强度的实质,因此采用有效应力法分析静水对土体稳定性的影响才是合理的(李广信,2010)。
另外,土体的含水量会对土的强度指标产生影响(李晓玮等,2017)。对于以石英为主的砂土,黏聚力在干态和在水下均为0,内摩擦角基本相同。对于一般的黏性土,土的黏聚力、内摩擦角会随着土的含水量的增大而减小,在饱和状态,运用不固结不排水试验测定的黏聚力降至0。
下面利用有效应力强度指标分别对砂土及黏性土的稳定性进行分析。
2.4.1 砂土
(1)数学分析法
静水中的土体可视为处于饱和状态,按有效应力原理,土体的总应力σ为有效应力σ 和孔隙水压力σu之和,即σ =σ +σu。 孔隙水压力在各个方位上大小相等,因此,静水中土体的最大、最小主应力也可表达为σ1=σ1 +σu和σ3 =σ3 +σu,其中,σ1 和σ3 分别为有效最大主应力和有效最小主应力(相当于干燥环境中的土体主应力)。
根据 τf =c +σ tanφ ,分析土体有效应力抗剪强度相对于总应力抗剪强度变化情况。因为砂土c =0,所以 τf =σ tanφ ,σ 不变,对于以石英为主的砂土,无水状态(干砂)和在静水中(饱和砂)土体的内摩擦角基本相同,因而抗剪强度τf 不变。而剪应力τ 不随孔隙水压力而改变,可见,按有效应力强度指标分析,静水中土体的稳定性不变。
(2)图形判断法
根据土的应力莫尔圆的变化,对土的破坏面上的应力状态的变化进行判别。
当砂土处于静水中时,受到围压作用,此时土体各个方向的总应力都增大σu,但最大有效主应力σ1 ,最小有效主应力σ3 均保持不变(图12)。其有效应力强度指标下的应力莫尔圆大小、位置均保持不变。此时,所有面(包括最易破坏的面)上的正应力σ 保持不变,各个面上的剪应力τ 保持不变。
根据土的强度包线和应力莫尔圆的相互关系(图13),对土的破坏进行判别:对于砂土,c =0,τf =σ tanφ 。对于以石英为主的砂土,在干态和在水下的内摩擦角基本相同,处于静水状态里的砂土,土的强度包线一定。而应力莫尔圆大小、位置较之无水状态下均保持不变,说明在有效应力强度指标下计算得土体稳定性不变。
2.4.2 黏性土
(1)数学分析法
根据2.4.1中砂土的公式推导,可知在静水中土体任一截面α上,采用有效应力指标计算的τ 、σ 与无水状态下的τ、σ均相等。对于处于饱和状态的黏性土,随着含水量的增大,土的c 、φ 均减小,而σ 不变,根据τf =c +σ tanφ ,可知抗剪强度τf 随之减小。
即采用有效应力强度指标下,水中的黏性土的所有面(包括最易破坏的面)上的剪应力τ 不变,而该面上的抗剪强度τf 减小,土体趋向于不稳定。
(2)图形法
当黏性土处于静水中时,受到围压作用,此时土体各个方向的总应力都增大σu,但最大有效主应力σ1 ,最小有效主应力σ3 均保持不变(图14)。其有效应力强度指标下的应力莫尔圆大小、位置均保持不变。此时,所有面(包括最易破坏的面)上的正应力σ 保持不变,各个面上的剪应力τ 保持不变。
根据土的强度包线和应力莫尔圆的相互关系(图15),对土的破坏进行判别:对于无水状态下的黏性土,其强度包线为斜直线①;处于静水中的飽和黏性土,φ 减小,c 减小,其强度包线为斜直线②;静水状态下有效应力莫尔圆的大小、位置较之无水状态下均保持不变,其图像越来越接近于强度包线,甚至与强度包线相切,说明在有效应力强度指标下计算得土体趋向于不稳定。
3 结论
(1)修建挡土墙、抗滑桩,加固基坑土体被动区是对土施加了侧向应力。简化后的应力状态为大主应力σ1不变,小主应力σ3增大。此时最易破裂面上的剪应力τ变小,而该面上的抗剪强度τf变大。图形上莫尔应力圆越来越远离强度包线,说明土体越来越趋向于稳定。
拆除围挡结构、坡脚卸载是减小了土的侧向应力。简化后的应力状态为大主应力σ1不变,小主应力σ3减小。此时最易破裂面上的剪应力τ增大,而该面上的抗剪强度τf减小。图形上莫尔应力圆越来越靠近强度包线,说明土体越来越趋向于不稳定,当τ增大到τf时,土体破坏。
(2)坡顶堆土、停放机械设备是增大了土的竖向应力。简化后的应力状态为大主应力σ1变大,小主应力σ3不变。此时最易破裂面上的剪应力τ比该面上的抗剪强度τf增大的速率快,图形上莫尔应力圆越来越靠近强度包线,说明土体越来越趋向于不稳定,当τ增大到τf时,土体发生破坏。
坡顶卸载是减小了土的竖向应力。简化后的应力状态为大主应力σ1变小,小主应力σ3不变。此时最易破裂面上的剪应力τ比该面上的抗剪强度τf减小的速率快,图形上莫尔应力圆越来越远离强度包线,说明土体越来越趋向于稳定。
(3)施加锚杆是增加了沿锚杆向土体内部的轴向力,简化后的应力状态为大主应力σ1变大,小主应力σ3变大。此时最易破裂面上的剪应力τ减小,而该面上的抗剪强度τf增大,图形上莫尔应力圆圆心向右移动,且越来越小,莫尔应力圆越来越远离强度包线,说明土体越来越趋向于稳定。
(4)对于处于静水状态下的砂土,采用有效应力强度指标计算的稳定性保持不变。对于处于静水状态下的黏性土,采用有效应力强度指标计算的稳定性,较之处于无水状态下的稳定性变小。
参考文献:
高大钊,2010. 岩土工程勘察与设计:岩土工程疑难问题答疑笔记整理之二[M]. 北京:人民交通出版社:586-588.
《工程地质手册》编委会,2018. 工程地质手册[M]. 5版. 北京:中国建筑工业出版社:246-284.
李广信,2010. 岩土工程50讲:岩坛漫话 [M]. 2版. 北京:清华大学出版社: 149-156.
李广信,张丙印,于玉贞,2013. 土力学[M]. 2版. 北京:清华大学出版社:168-179.
李晓玮,刘翠娜,2017. 稳定渗流條件下挡土结构水、土压力分布探讨[J]. 城市地质,12(3):36-40.
松岗元,2001. 土力学[M]. 罗汀,姚仰平,译. 北京:中国水利水电出版社:134-138.

