委托计算下基于区块链的公平支付方案

李沓，田有亮,3，向康，高鸿峰

（1.贵州大学计算机科学与技术学院，贵州 贵阳 550025；2.贵州大学密码学与数据安全研究所，贵州 贵阳 550025；3.贵州省公共大数据重点实验室，贵州 贵阳 550025；4.贵州大学网络与信息化管理中心，贵州 贵阳 550025）

1 引言

随着大数据、云计算的迅速发展，数据的处理及存储能力受到越来越多的重视。一些自身能力有限的委托方往往需要将复杂的计算任务委托给计算能力强的计算方。而在实际环境中，无论是委托方还是计算方，都是理性参与者，都希望让自己的利益最大化。

传统委托计算过程中，需要对计算方返回的结果进行验证从而保证结果的准确性。Xu 等[1]提出在不使用昂贵的完全同态加密的情况下，诚实但好奇的第三方可以帮助验证外包计算任务的结果，而不需要学习计算任务或其结果。通过在参数系统模型中结合新颖的承诺协议和加法同态加密来保护计算任务和来自不受信任的第三方验证者的结果。Wang 等[2]为了解决传统的VC（verifiable computation）问题，提出了一种可验证的外包计算，具有完全委托FD-VC（verifiable out sourced computation with full delegation），通过将预处理委托给云，大大降低了客户端的计算成本。Zhao 等[3]使用加同态加密技术和混淆电路构造了可验证计算方案。现有的对于委托计算结果的验证方案大多采用第三方或者处理速度较慢的加密技术。虽然保证了结果的正确性，但会泄露参与方的隐私而且极大地增大了委托方的开销。

而在实际环境中，由于参与者的自利性，众多学者利用博弈论研究委托计算中参与者之间的关系，从而保证计算方诚实进行计算从而取缔第三方验证过程。Yin 等[4]基于博弈论研究了委托计算的验证复杂问题，提出了基于比特币和Micali-Rabin的随机向量表示技术的公平理性委托计算协议。该协议不仅解决了传统委托计算验证复杂的问题，而且保证了诚实参与者的利益。Li 等[5]利用博弈委托代理理论，构造委托计算博弈模型并结合全同态加密技术构造理性委托计算协议保证了参与者双方的利益。Dong 等[6]利用博弈论和智能合约技术来激励云之间的约束、背叛和不信任，这样理性云就不会串通和欺骗。在没有串通的情况下，通过交叉检查来自2 个云的结果，可以容易地验证外包云对用户计算任务的正确性。

但在委托计算的支付过程中，计算方的作假行为和委托方的抵赖行为会使诚实参与者的利益受到损失。因此，既要保证诚实的参与者的利益，又要对恶意的参与者进行惩罚。目前，越来越多的研究者基于区块链技术及比特币系统来研究支付的公平性。Zhang 等[7]提出了一种基于区块链的公平支付框架BCpay，用于云计算中的外包服务，保证了参与者的利益不受损失。Andrychowicz 等[8-9]利用比特币系统保证双方安全通信协议的公平性，并设计了一种安全的双方协议，以实现从一方到另一方的“强制”财务转移的功能。Bentov等[10]研究了安全计算中的公平模型，并展示了在比特币网络中如何在双方和多方环境中实现。Wang 等[11]提出了基于智能合约的可审计的公平支付和实物资产交付协议。利用区块链的可追溯性和可审计性为整个运输中的资产和数据共享提供了有效的方法。Yu 等[12-13]为了防止比特币的双花攻击，设计了公平存款以抵御双重支出。公平存款既保证了支付过程中的付款方因双倍花费而受到处罚，又保证了受害者的损失得到赔偿，保证了在支付过程中的公平性。Baza 等[14]提出了一种基于公共区块链的分散式乘车共享服务B-Ride，利用智能合约和零知识集成员证明引入时间锁定存款协议来实现位置隐私隐藏以及公平付款。Zhao 等[15]提出了一种名为 SPS（secure pub-sub）的新架构，去除了第三方，基于区块链的公平支付和声誉实现数据的机密性和可靠性、订阅者的匿名性及发布者和订阅者之间的支付公平性。Huang 等[16]提出了一种新的基于比特币的外包计算公平支付方案。因为比特币语法的优点，用户可以直接进行交易而不需要银行。Liu 等[17]为实现加密货币支付收据之间的公平交换，引入了公平交换协议的强时效性概念，并提出了2 个公平的收款协议实例，利用区块链的功能来实现强大的及时性。

当前，基于区块链技术的支付方案中主要利用了比特币系统的去中心化特性，保证了支付过程中参与者的公平性。但多数方案中是针对结果验证后进行奖惩，不仅耗费参与方的代价，而且验证过程的效率较低。博弈论在研究经济体制中有独特的地位，因此利用博弈论分析支付过程的纳什均衡解可以很好地保证双方诚实选择行为策略，从而提高委托计算的效率，降低委托方的成本。

本文结合博弈论与区块链技术提出了基于区块链的公平支付方案，实现了委托计算支付过程下的纳什均衡解。所提方案首先保证了参与方诚实执行策略，其次保护了参与方的隐私，最后实现了对诚实参与者的奖励以及恶意参与者的惩罚。本文的具体工作如下。

1)利用博弈论刻画了委托计算中参与方在支付过程中的博弈模型，并给出了唯一的纳什均衡解。

2)利用区块链技术提出委托计算过程中计算方的信誉值模型，并实现不可篡改。

3)提出基于比特币时间承诺技术的公平支付协议，实现委托计算下支付的公平性。

4)对协议的安全性与性能进行分析，证明协议的安全性，并且保证参与者在支付过程中诚实选择行为策略。

2 准备知识

2.1 委托计算

委托计算[18]主要是指委托方由于自身计算能力不足或资源受限而无法计算一个复杂任务，将复杂任务委托给一个计算能力强的计算方，由计算方返回一个正确计算结果而委托方支付相应报酬。但在实际环境中，由于参与者双方的自利行为，支付过程中存在计算方作假以及委托方抵赖等行为。

传统委托计算主要分为两类，分别是基于复杂性理论构造方案和基于密码技术构造方案。传统的委托计算方案主要利用PCP（probabilistic checking of proof）定理、全同态加密、混淆电路等技术进行方案构造，通常假设委托方是诚实的，对计算方返回结果进行公开验证。而在现实环境中，由于参与者有一定的偏好取向，不能保证参与者都是诚实的，因此出现了理性委托计算。

理性委托计算假设参与者都是理性的，其目的是最大化自身效用，利用博弈论分析参与者的行为策略从而获得纳什均衡解，使参与者双方诚实选择行为策略，保证委托计算结果的正确性及参与者双方的公平性。

2.2 比特币交易

比特币[19]由中本聪于2008 年提出，比特币没有发行机构，它依据特定算法，通过大量的计算产生，通过整个网络中的所有节点达成共识来确认并记录所有的交易行为。

比特币交易[8]Tx 的最常见形式为

((y1,a1,σ1),…,(yn,an,σn),(v1,π1),…,(vm,πm),t)

Tx 的输入是三元组 (y1,a1,σ1),…,(yn,an,σn)，其中 yi是某个先前事务的哈希值，ai是输出的索引，iσ 称为输入脚本。Tx 的输出是一对对的列表 (v1,π1),…,(vm,πm)，其中 vi是Tx 的第i 个输出值，iπ 是输出脚本。t 是时间锁定，表示Tx 仅在时间范围t 内有效。

2.3 比特币时间承诺

Andrychowicz 等[8-9]基于比特币系统构建了一种定时承诺，其中提交者必须在特定时间范围内揭示其秘密，否则提交者需要支付罚款。

比特币时间承诺方案由CS(S,C,d,t,s)表示，在委托计算中此承诺方案在计算方S 和委托方C 之间执行，其中计算方S 充当提交者，委托方C 充当接收者，s 表示计算方与委托方各自的秘密值。具体地，S 承诺秘密并且必须在特定时间t 之内打开承诺以赎回他的存款d。否则，存款将支付给C。承诺方案包括3 个阶段。

1)承诺阶段CS.commit(S,C,d,t,s)

2)打开阶段CS.open(S,C,d,t,s)

3)惩罚阶段CS.fine(S,C,d,t,s)

2.4 博弈论

博弈论[20]是研究一些人或者团体在某种特定的环境下如何进行决策及决策均衡问题的理论，在委托计算的过程中，由于委托方和计算方都有自利行为，因此，可用博弈论来分析双方的行为。

定义1博弈表达的基本形式[21]由局中人集合P、策略空间Y 和效用函数u 这3 个要素组成，即G={P,Y,u}，其中P={ P1,…,Pn}，Y={Y1,…,Yn}，u={ u1,…,un}。效用函数 ui:Y→ R（R 代表实数空间），它表示第i 个局中人在不同组合下所得的效益。

3 支付博弈模型

在委托计算的支付过程中，由于参与者双方的自利行为，使实际结果出现偏差。对于委托方而言，只想得到计算的正确结果而不想向计算方支付服务费，这将导致计算方即使提供了正确的结果依然得不到相应的奖励。对于计算方来说，只想得到奖励而不想提供相应的计算服务，这将导致委托方在支付了相应的服务费之后不能得到正确的结果。本文基于博弈论的角度分析了委托计算过程中支付的博弈模型，其支付博弈树如图1 所示，其中，S 表示计算方，U 表示委托方，Si表示计算方的收益，Ui表示委托方的收益。

图1 支付博弈树

假设存在一次委托任务，使委托方得到计算结果后的收益为P，委托方需要支付的服务费为T，计算方在收到任务后完成正确结果需要耗费的成本为S。由于参与者双方都有自利行为，为了防止参与者双方做出欺骗的行为，假定委托方在发布任务的时候需要支付押金Q，计算方在接受任务时需要支付押金R，其中，Q ＞ P ＞T，S ＜ T ＜R 。基于博弈模型的分析，可以得到如表1 所示的委托方和计算方的交付效用矩阵，根据参与方各自的行为得到最终的效用函数。

表1 支付效用矩阵

由效用矩阵可以看出，委托方和计算方在此次委托任务过程中的唯一纳什均衡解是双方都做出诚实的行为，只有这样双方的利益才不会有损失。无论哪一方做出恶意行为，做出恶意行为的一方将会损失自身的利益。若双方都做出恶意行为，则双方都将受到惩罚，损失自己的利益。

4 系统模型

本节主要介绍系统模型，系统模型如图2 所示。在此模型中，计算方首先上传自己的信誉值到区块链上，委托方查看区块链根据不同的任务需求选择相应的计算方进行任务发布。然后计算方与委托方共同创建公共存款交易，若参与者双方诚实执行策略，则基于公共存款交易创建支付交易完成委托计算的支付。若参与者存在不诚实行为，则根据公共存款交易创建打开惩罚交易实现对诚实参与者的奖励以及恶意参与者的惩罚。

图2 系统模型

4.1 计算方信誉度模型

每个计算方基于它的交易历史或者工作性质都会形成相对应的信誉值。在本文中，由于计算任务需求的不同往往需要不同的计算方。在委托计算的过程中，计算方信誉度的取值由于在社会网络中的关系很难量化，所以本文基于计算方的交易历史进行信誉值评估。

4.1.1 本地信誉值

计算方在一次交易后有2 种状态，分别是诚实评价和不诚实评价。每一次交易完成后计算方都将计算自己的信誉值。由于委托的任务有相应的要求，故不同的任务对应不同的难度系数。在一次交易中，任务要求越高，难度越大，其复杂度系数越大，反之则越小。由此，计算方的本地信誉值计算模型为

其中，Lcred 表示计算方的本地信誉值，T(t)表示计算方总的交易次数，H(t)表示计算方总交易次数中诚实交易的次数，D 为一次交易中任务的复杂度系数。

4.1.2 全局信誉值

在一次委托计算任务完成后，计算方计算自己的本地信誉值并与上一次的全局信誉值进行运算，然后得到此次委托计算的全局信誉值并进行签名上传到区块链上，此全局信誉值计算模型可以表示为

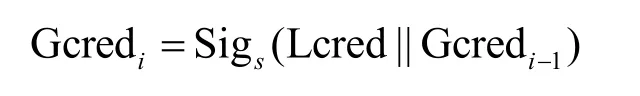
其中，Gcred 表示计算方的全局信誉值。

信誉值是计算方可以得到计算任务的基础，委托方根据不同的任务需求选择相应的计算方进行委托。计算方的信誉值越高，其被选择的概率越大。全局信誉值是将计算方的信誉值形成可信链，在每一次任务完成后计算方都需要更新自己的全局信誉值并重新上传。

4.2 任务发布

委托方由信誉值链可查看计算方的全局信誉值，然后根据任务难度选择相应的计算方发送任务进行委托。任务公告如图3 所示。

假设委托方U 具有密钥对(pku,sku)，则Sigu(m)表示与sku相关联的消息m 上的ECDSA签名，Veru(m,β)表示消息m 上关于pku的ECDSA签名β 的验证结果。因此，Sigu(task-claim)表示委托方U 对任务公告的签名；name 表示任务的名称；requirement 表示任务的要求；complexity factor 表示任务的复杂系数；K 表示任务完成后计算方应获得的报酬；T 表示任务完成的截止时间。

图3 任务公告

委托方发送任务成功后，创建委托方存款交易TxU，值为d。此交易包含委托方的签名及委托方的秘密用于创建公共承诺交易，如图4 所示。

图4 委托方存款交易

4.3 计算方接收任务

计算方接收来自委托方发出的任务公告，根据公告内容计算此次委托计算的代价。若计算代价大于所得报酬，则计算方不予计算；若计算代价与所得报酬相等，则计算方可以选择接受或者拒绝；若计算代价小于所得报酬，则计算方接收此任务。如果计算方没有在规定时间内提交任务，需要支付一定的赔偿。因此当计算方接受任务时需要向区块链创建一个存款交易TxS，此存款交易如图5 所示。计算方计算代价模型如下。

设price 表示计算方的总开销。有

其中，A 表示此次委托计算的服务费；accept 表示计算方接受此次任务；refuse 表示计算方拒绝此次任务。

计算方接受任务并创建一个存款交易TxS，此交易包含计算方的签名及计算方的秘密用于创建公共承诺交易。

图5 计算方存款交易

4.4 创建公共承诺交易

委托方与计算方创建公告承诺交易commit，并最终发布在区块链上。commit 由(U ,S,d,t,s)表示，其中，U 和S 是执行协议的双方，分别代表委托方和计算方；d 是commit 中存款的价值；t 为时间范围，表示参与者双方应该在时间t 之前履行承诺，打开交易获取存款。承诺阶段由commit(U ,S,d,t,s)表示，打开阶段由open(U ,S,d,t,s)表示，惩罚阶段由punish(U ,S,d,t,s)表示，支付阶段由pay(U ,S,d,t,s)表示。

4.4.1 准备阶段

U 和S 各自生成密钥对u 和s。Su和 Ss是U,S 各自的秘密，并且区块链上包含未兑换的交易TxU 和TxS，两者值都为d，分别可以用 Su和 Ss进行兑换。hu和 hs分别表示对U 和S 各自秘密的哈希值，其中，hu=H(Su|| ρu)，hs=H(Ss|| ρs)，ρu←{0,1}α和ρs←{0,1}α，α 是安全参数。

4.4.2 承诺阶段

委托方和计算方分别利用TxU 和TxS 作为输入计算交易commit，如图 6 所示，委托方对commit 进行签名后发送给计算方，如果在广播的最大时延之前计算方都没有收到commit，则计算方收回自己的押金并退出。若计算方收到了commit，则计算方对其签名后进行广播。委托方等到commit 出现在链上，如果在广播的最大时延之前commit 没有出现在链上，则委托方收回自己的服务费并退出。若commit 出现在链上，则承诺完成，计算方开始完成相应任务。创建commit 交易的流程如算法1 所示。

图6 承诺交易

算法1commit

输入Sigu[TxU]，Sigs[TxS]，S's，S'u，Du，Ds

输出commit

4.4.3 打开阶段

委托方和计算方在commit 交易情况下承诺对自己的行为进行负责。若出现不诚实的行为，则委托方和计算方依然可以得到各自的服务费或押金。原因如下。

委托方在支付阶段如果不履行诺言，不用自己的秘密打开支付交易。则计算方基于承诺交易commit创建计算方打开交易openS 赎回自己的押金。

计算方在不能提供正确的服务证明情况下却不向委托方支付赔偿，则委托方基于承诺交易commit 创建委托方打开交易openU 赎回自己的押金。openS 与openU 如图7 所示，创建openU 与openS 交易的流程如算法2 和算法3 所示。

算法2openU

输入Sigu[commit]，Sigs[commit]，Proof，T

输出openU

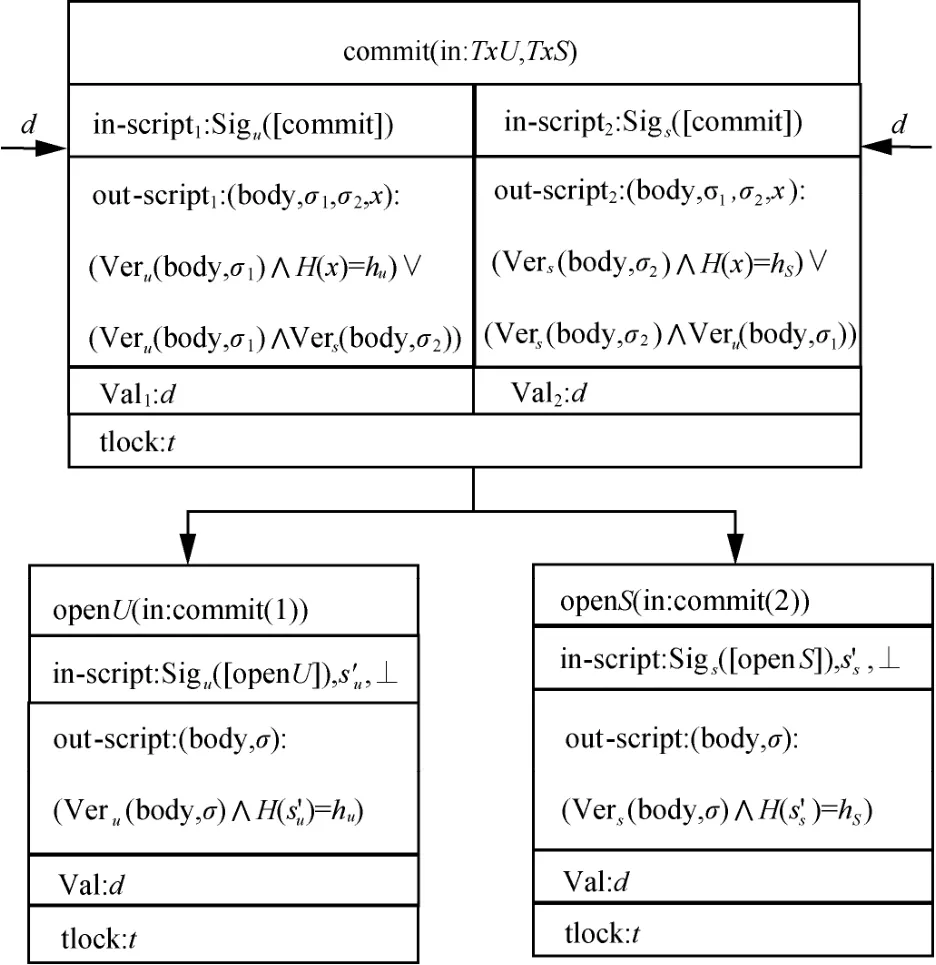
图7 打开交易

算法3openS

输入Sigu[commit]，Sigs[commit]，Proof，T1，T2

输出openS

4.4.4 惩罚阶段

若在任务截止时间t 之前，计算方不能给出相应的工作证明，则委托方可以基于commit 创建委托方惩罚交易punishS，此交易值为计算方所交的押金，在全网公告后，所有链上节点达成共识，则委托方可以基于他的签名和秘密来兑换此交易获得对计算方的罚金。

若计算方的工作证明得到证实，但是委托方在打开阶段抵赖不承认计算方的工作并且不参与兑换打开交易。则计算方可在服务证明证实之后，基于commit 创建计算方惩罚交易punishU，此交易的值为委托方的押金，待链上节点达成共识后可基于计算方的签名和秘密来兑换此交易。惩罚交易如图8 所示，创建委托方和计算方惩罚交易的流程如算法4 和算法5 所示。

图8 惩罚交易

算法4punishU

输入Sigu[commit]，Sigs[commit]，Proof，T

输出punishU

算法5Punish S

输入Sigu[commit]，Sigs[commit]，Proof，T1，T2

输出punishS

4.4.5 支付阶段

在计算方提供正确的服务证明之后，委托方和计算方基于commit 创建支付交易pay，交易值包括委托方的服务费d 以及计算方预存的押金d，委托方和计算方用各自的秘密共同打开此交易，然后计算方获得最后金额。支付交易如图9 所示，创建支付交易的流程如算法6 所示。

算法6pay

输入Sigu[commit]，Sigs[commit]，Proof

输出pay

4.5 更新信誉值

待一次交易完成后，计算方根据此次交易记录更新自己的信誉值并重新上传到区块链上，等待下一次交易的启动。委托方在发布任务的时候可以从区块链上查看计算方的信誉值。每一次交易过程中委托方都能知道计算方在上一次交易中的状态，这样不仅帮助委托方按需选取相应的计算方，同时使计算方遵守协议规定，做出诚实的行为。

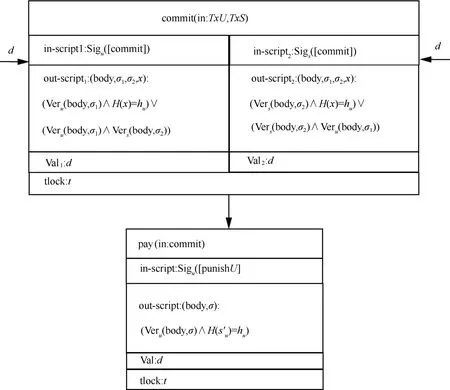
图9 支付交易

5 协议分析

5.1 安全性分析

本文的安全性主要从以下2 个方面来考虑。

定理1如果基于ECDSA 的签名是不可伪造的且选取的哈希函数是抗碰撞的，那么委托方和计算方的支付是安全的。

证明委托方和计算方在支付时需要验证各自的签名以及各自秘密的哈希值是否正确。只有签名和秘密的哈希值都正确的情况下才能创建交易获取相关比特币押金。

假设存在敌手EvE 在一次委托计算中伪造委托方签名Sigu′，伪造计算方签名Sigs′，伪造委托方秘密值为X′，伪造计算方秘密值为Y′。敌手为了获取比特币押金，利用伪造签名以及秘密值创建打开与惩罚交易，EvE 的具体操作如下。

1)获取公共存款交易commit。

2)使用伪造的委托方签名Sigu′、计算方签名Sigs′及各自秘密值X′和Y′，时间承诺T 和计算结果证明Proof 。

3)计算秘密哈希值，hu′=H(X ′|| ρu)，hs′=H(Y ′|| ρs)。

4)验证签名和秘密值的哈希值是否正确。

Veru′[commit,Sigu′]==true&&hu′=hu

Vers′[commit,Sigs′]==true&&hs′=hs

5)创建打开与惩罚交易转移比特币押金。

若敌手最终获取了比特币押金则说明敌手伪造的签名可以验证通过，且敌手伪造的秘密值能够通过哈希运算与最终的哈希值相同。这与假设相矛盾，故敌手不可能创建打开或惩罚交易，获取比特币押金。

同理可得，在支付交易验证中，敌手的验证也不可能通过。这意味着敌手创建的支付交易不能在链上被广播，因此交易不被承认，故敌手不能获取服务费。

在链上的所有交易当且仅当签名和秘密值验证通过，才能获得比特币押金。而基于ECDSA的签名是不可伪造的且选取的哈希函数是抗碰撞的，所以对于委托方和计算方而言支付是安全的。

证毕。

定理2若基于ECDSA 的签名不可伪造，则计算方的全局信誉值是不可篡改的。

证明由计算方的全局信誉值计算模型可知

Gcredi=Sigs(Lcred||Gcredi-1)，假设存在敌手伪造计算方的签名Sigs′，则敌手具体操作如下：

1)敌手通过伪造的签名对计算方的信誉值进行签名，同时上传至区块链。若信誉值在链上广播并最终记录，则说明敌手伪造的签名验证通过。这与假设相矛盾，故计算方的信誉值不可能被敌手上传至区块链。

2)恶意计算方伪造本地信誉值参与计算全局信誉值。因为计算方的交易历史在区块链上公开可见，若存在恶意计算方伪造信誉值进行计算，则节点验证不能通过，故不能达成共识，全局信誉值不会被广播记录。

证毕。

5.2 正确性分析

定理3基于比特币时间承诺的公平支付协议具有正确性，而且可以保证双方达到唯一纳什均衡解。

证明在承诺阶段若委托方U 和计算方S 诚实执行该策略，则双方共同创建交易commit，交易commit 包含了委托方的押金Q 和计算方的押金R，计算方诚实进行计算最终委托方获得收益P，计算方花费成本S，而委托方需要支付的服务费为T。

若委托方U 选择诚实策略，计算方S 选择恶意策略，则委托方获得效用Q+T +R，计算方获得效用-R 。

若委托方U 选择恶意策略，计算方S 选择诚实策略，则委托方获得效用-(Q+T)，计算方获得效用Q+R+T-S 。

若委托方U 和计算方S 均选择恶意策略，则委托方获得效用-Q，计算方获得效用-R 。

若委托方U 和计算方S 均选择诚实策略，则委托方获得效用Q+P-T，计算方获得效用R+T-S 。

在博弈模型中，由于支付效用有如下关系Q ＞ P ＞T，S ＜ T ＜R，只有当参与方都选择执行诚实策略，委托方U 和计算方S 才能获得最大效用，此时双方达到唯一纳什均衡解。

由协议分析可知，因为参与者双方皆为理性，故为了使自己的利益最大化，双方都会诚实执行策略，故协议具有正确性。

证毕。

6 性能分析

下面对本文所提方案的时间开销进行评估。本文所提方案时间开销主要包括创建公共承诺交易时间以及创建打开、惩罚交易时间。而比特币系统平均10 min 产出一个块，因此将创建公共承诺交易时间设为10 min。即创建公共承诺交易时间如图10中曲线y1所示。本文主要考虑委托任务量与耗费时间的关系，在传统委托计算方案中，需要对计算方返回结果进行验证，因此会耗费大量的验证时间，随着任务量的增加，验证时间也随之增加，如图10中曲线 y2所示。而本文所提方案中理性委托方不需要对返回结果进行验证，仅在创建公共承诺交易时间的基础上增加创建打开交易与惩罚交易的时间，如图10 中曲线 y3所示。对比传统委计算方案，本文所提方案提高了效率。

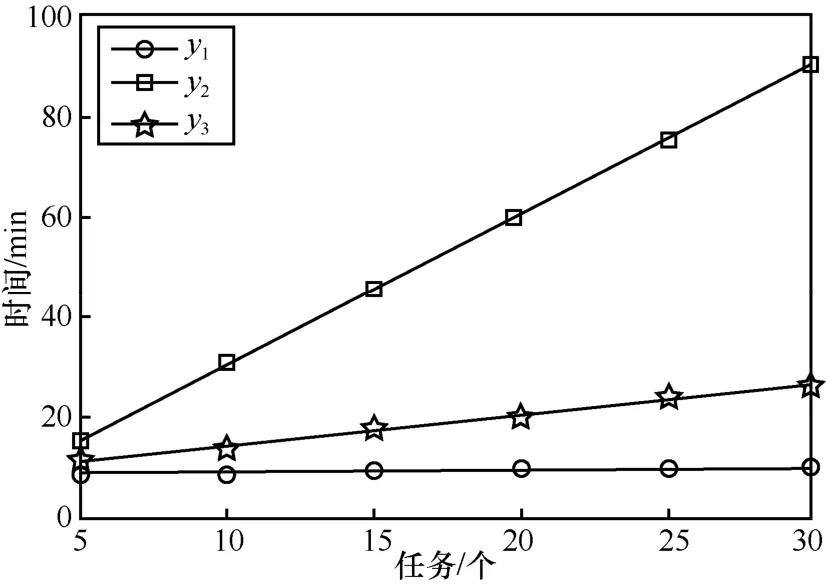
图10 方案时间开销

下面将本文提出的委托计算公平支付协议与现有的委托计算协议进行比较。表2 将从委托计算的参与方隐私性、委托方公平性以及计算方公平性等方面与其他方案进行对比，其中“√”代表满足该性能，“×”代表不能满足该性能。

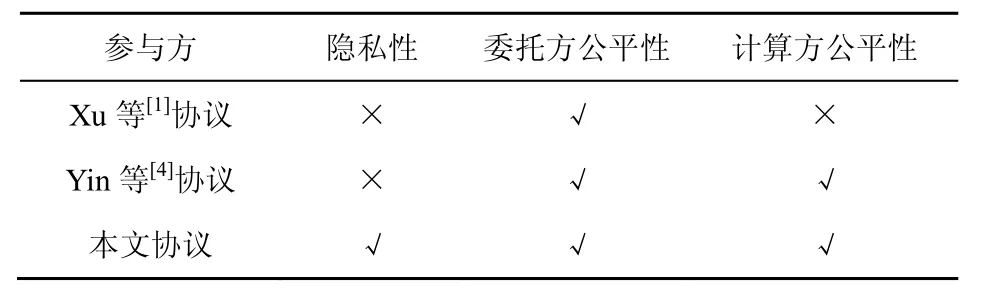
表2 本方案与其他方案性能对比

Xu 等[1]提出的协议中采用诚实但好奇的第三方帮助验证委托计算任务的结果。通过在参数系统模型中结合承诺协议和加法同态加密来保护计算任务和来自不受信任的第三方验证者的结果，保证了计算方诚实计算结果，即保证了委托方的公平性。但由于方案中采用了第三方来帮助验证计算结果，因此容易泄露参与者的隐私，且无法保证最终计算方可以得到相应的服务费，不能保证计算方的公平性。

Yin 等[4]提出的理性委托计算协议中引入了可信第三方帮助委托方和计算方取回押金。通过委托方和计算方预存押金的形式保证公平性。一旦一方违反承诺，则另一方可以联合可信第三方取回押金来保证协议的公平性。但是协议中依然存在第三方，故容易泄露参与者的隐私。

本文提出的委托计算公平支付协议利用博弈论构建支付博弈模型，并分析了唯一的纳什均衡解，利用效用函数约束参与者双方诚实执行策略，从而保证了委托方的公平性，并取缔了委托计算中结果的验证过程，提高了效率。利用比特币押金保证了计算方的公平性并且不需要第三方进行验证从而保护参与方的隐私。此外，利用区块链的激励机制与计算方的信誉机制相结合提高了委托任务的通信效率。

7 结束语

本文基于博弈论分析了委托计算中支付的公平性，同时利用比特币时间承诺提出了一种在委托计算中保证公平性的支付方案，保证了参与方能够诚实选择行为策略。利用区块链去除了第三方来保证参与者的隐私而且实现责任溯源。如何减少协议的通信复杂度以及确定时间承诺的极限值将是下一步研究的工作。