水平地震作用下大式带斗栱木结构古建筑的抗倒塌性能分析

张锡成，胡成明，吴晨伟，马赫迪，韩乙楠

(1． 西安建筑科技大学土木工程学院，陕西西安 710055； 2． 结构工程与抗震教育部重点实验室(西安建筑科技大学)，陕西西安 710055；3． 陕西省结构与抗震重点实验室，陕西西安 710055)

0 引 言

建筑物在经历水平地震作用后会产生各种不同程度的破坏，其中倒塌破坏是造成人员伤亡和财产损失的直接原因。而对于木结构古建筑而言，形势则更加严峻。由于木材这种天然材料本身就具有一定缺陷，比如干缩开裂、易燃易朽等，再加上木材在外界复杂环境中使用发生性能退化，以及长期以来对木结构古建筑保护方面的忽视，那些仅有的古建筑木结构正处在濒临破坏的危险状况之中。在2008年汶川地震中，许多寺庙的木结构古建筑发生局部破坏和整体倒塌[1]，如都江堰市二王庙木结构建筑的柱脚落架导致屋盖倾斜(图1a)，以及柱脚产生滑移变形(若此变形过大，则会造成结构倒塌)(图1b)。

图1 汶川地震中木结构古建筑的局部破坏

目前，从倒塌破坏机制及抗倒塌性能的方面对木结构古建筑进行的研究相对较少。国内相关研究[2]大致将木结构古建筑有可能存在的倒塌机制分为了四类(柱脚滑移量过大引起的结构落架机制、铺作层滑移过大产生的屋盖塌落机制、榫卯节点丧失承载力导致的层倒塌机制，以及整体倾覆机制)，并且初步分析了各倒塌机制中出现倒塌临界点的位置，但上部结构在分析时简化为刚体，对木结构古建筑中所具有的结构特性的考虑不够全面，因此计算模型过于简略。我国古建筑木结构维护与加固技术规范(GB 50165—92)[3]中也未涉及倒塌评估方法及倒塌临界点限值的取值，仅规定了抗震变形验算中木构架的位移角限值。在国外的相关研究中，日本学者Nakagawa和Ohta[4-5]对动力荷载作用下日式传统民居模型的破坏过程进行了试验研究，但其试验模型与中国传统木结构建筑在形制构造及连接方式上差异较大。因此，从倒塌机制方面对国内的木结构古建筑的抗倒塌性能进行研究，对其抗震性能分析和后期维修加固十分必要。

1 木结构古建筑倒塌破坏的判定准则

通过相关的振动台试验[6-7]以及对大量的震后灾害调查分析[1]可以总结出：木结构古建筑出现结构落架破坏和层间倒塌破坏的主要原因是柱脚滑移量过大或者柱架侧移变形过大。因此，需要对以上两种倒塌机制进行深入的研究。首次超越破坏以及累计损伤破坏是目前针对结构倒塌最常使用的两种判定准则。其中，针对木结构古建筑特殊的结构形式及特点，选用首次超越破坏对其倒塌破坏进行判定，认为结构在地震作用下的任意判定指标(如构件强度、层间位移或延性系数等)大于规定值时结构即发生倒塌，而累计损伤破坏多应用于现代结构倒塌判定中，总的来说，首次超越破坏含义明确且相较于累计损伤破坏更适用。

1．1 柱脚滑移倒塌机制

按照宋代《营造法式》[8]的相关制作要求，柱径大小是确定础石尺寸的主要依据。因此，础石大小是研究柱脚滑移倒塌机制的重要参数。假设当础石在受到地震作用后，其相对于地面不发生运动且没有破坏产生。如果此时古镜(柱础的顶面)半径开始小于柱与础石之间的最大滑移变形时，上部结构则会由柱脚滑出础石导致落架。同时，根据课题组相关的振动台试验[9]，可以将础石半径与柱脚处产生的最大滑移量是否相等作为判断结构是否处于临界倒塌状态的依据，如图2所示。

图2 柱脚滑移倒塌的临界状态

故可以定义滑移倒塌参数为柱脚在受到地震作用后所产生的最大滑移量xmax。根据图2所示，即可给出柱脚滑移倒塌的相对位移判定准则：

xmax>x

(1)

式中：x为柱脚滑移倒塌破坏时柱脚的临界滑移量，而

x=t+D/2

(2)

式中：t为础石外边缘至木柱外表面的距离；D为柱直径。

1．2 榫卯节点破坏导致的层倒塌机制

根据课题组相关的振动台试验[9]现象可分析得知，大式带斗栱木结构古建筑在受到水平地震作用后最终发生整体倒塌，其倒塌机制正属于层倒塌机制。此机制产生的主要原因为结构在外部激励作用下产生的大幅度变形导致榫卯节点承载能力及刚度难以承受上部屋盖经斗栱传递下来的荷载，从而结构发生倒塌破坏。此时，结构产生变形主要是由于柱架产生侧移，如图3a所示。由于斗栱层产生的变形较小，所以仅考虑柱架侧移变形为整个结构的变形，其中θ为柱架变形层间相对转角，如图3b所示。

图3 水平地震作用下结构的变形

柱架在受到水平地震作用后所产生的侧移变形必定会导致平置在础石之上的柱脚转动。但考虑到斗栱的变形不大，故可将栌斗中心作为承受上部屋盖荷载的受力位置，如图4所示。图4中，umax为柱架最大相对侧移变形值，h为柱架高度。

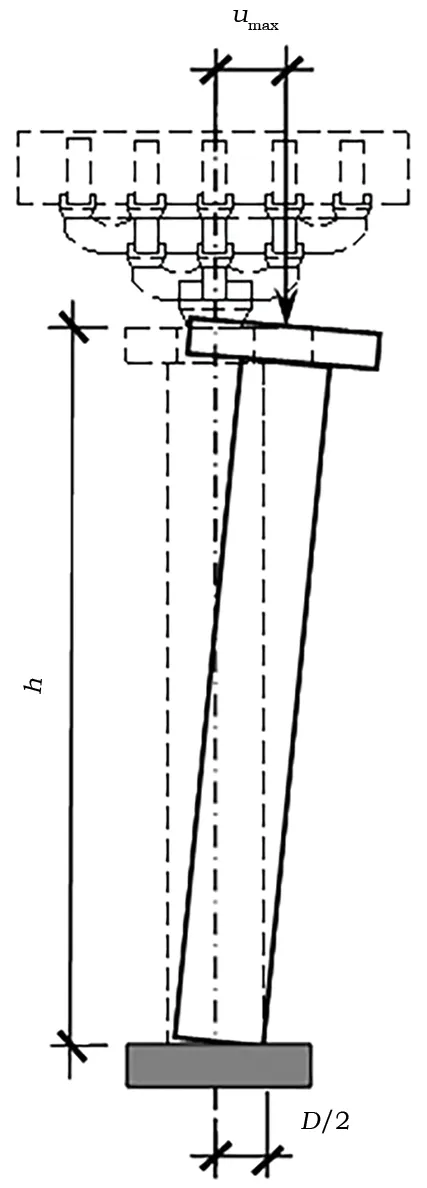
图4 柱架的变形及受力示意图

从图4可以看出，当柱径小于两倍的柱架相对侧移，即

umax>D/2

(3)

时，屋盖的大质量造成重力的二阶效应的产生，导致结构变形增大。此时，节点会因为柱头与额枋连接的榫头从卯口拔出，从而丧失结构承载能力。因此，当出现式(3)所示情况时，即可认定结构已发生层间倒塌。

由于式(3)所给出的柱径不具有通用性，因此层间倒塌准则可选用层间相对位移角θ进行表示，即：

θmax>θ

(4)

式中：θmax为柱架最大层间位移角计算值；θ为结构倒塌时层间位移角限值，θ=D/2h。

柱径与柱高比值D/h在大式木结构古建筑中通常取1∶10.5～1∶9.5之间[10]。因此，中间值θ=1/20 rad可作为层间位移角限值。

通过课题组完成的殿堂式结构振动台试验分析[7]得知，在地震激励为900 gal时，榫卯节点破坏十分严重，卯口处已被撕裂，结构处于倒塌状态中，此时层间位移角已达到限值1/21。日本学者的振动台试验[11-12]同样得出当层间位移角超过1/20时，结构有大概率会倒塌。因此，倒塌层间位移角限值选取为θ=1/20 rad是符合实际情况的。

2 大式带斗栱木结构古建筑抗倒塌性能分析

2．1 模型建立

以课题组参照宋代《营造法式》制作的某单层单开间殿堂式木结构模型为研究对象[9]，建造的缩尺模型及燕尾榫节点尺寸如图5所示。采用ANSYS软件建立该模型的空间杆系有限元模型，如图6所示。其中，采用COMBIN40单元模拟柱与础石间的滑移连接特性；柱、阑额及梁构件采用BEAM188单元模拟，木材的正交各向异性通过材性试验数据[9]赋予该单元沿三个方向的弹性模量及泊松比模拟，模型所使用的红松密度取为440 kg/m3；斗栱在荷载作用下的力学特性由COMBIN39+COMBIN14组合单元模拟；榫卯节点的半刚性性能采用COMBIN39单元。基于课题组进行的与振动台模型相同尺寸的斗栱及榫卯节点低周反复荷载试验[13-15]，根据水平力-侧移曲线定义COMBIN39弹簧单元的实常数；由于竖向力与竖向位移近似呈线性关系[13]，单朵斗栱的竖向刚度由试验数据线性拟合为K=6 kN/mm，斗栱的轴向性能由COMBIN14单元的实常数项模拟；根据力-位移曲线定义COMBIN39弹簧单元的实常数。屋盖以及梁架结构的自重可看作由其下部四朵斗栱共同承担，将其质量集中在斗栱顶部。

图6 有限元模型

通过柱与础石间的静摩擦试验[16]测定静摩擦系数平均值μs=0．33，COMBIN40单元的临界滑动力FSLIDE=μsmg，水平刚度K1=∞，K2=0，有限元单元GAP=C=0。用正比于单元初始刚度的单元阻尼模拟古建筑中榫卯及斗栱的阻尼性能。

利用ANSYS软件对提出的空间杆系动力有限元模型进行非线性动力分析，以模拟木结构古建筑的两种倒塌机制。采用国际上通用的增量动力分析(incremental dynamic analysis，IDA)方法[17]检验结构的抗倒塌性能。

2．2 有限元模型的试验验证

2．2．1模态分析 为了验证所建立模型的有效性，对有限元模型进行模态分析，并将得到的固有频率以及模态振型与原始结构进行对比。表1为计算模型前六阶自振频率及周期。图7为计算模型的前六阶模态振型，并给出了模型变形前后的位置。

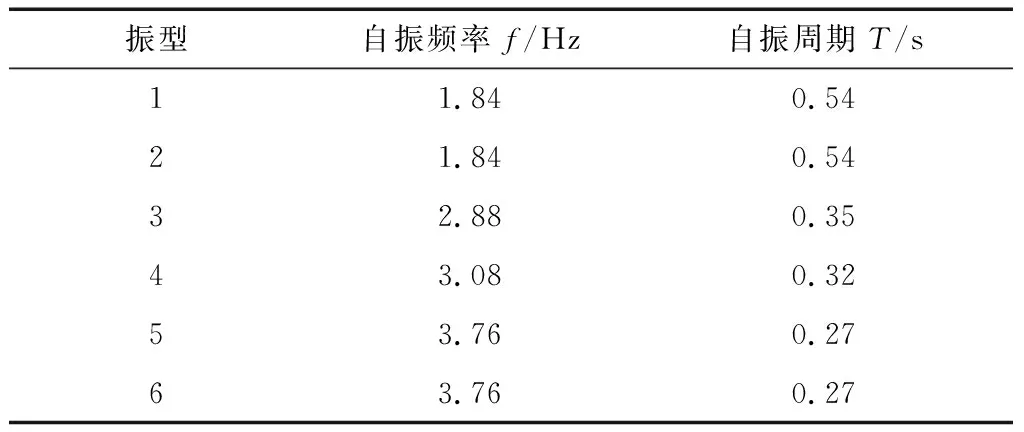
表1 计算模型的自振频率及周期

从表1可知，计算模型的第一阶振型对应的频率为1．84 Hz，而通过对课题组振动台试验模型的模态分析得到模型自振频率为2．05 Hz[7]，两者之间的误差仅为10．24%，属于可接受误差范围之内。由于计算模型在简化过程中忽略了普拍枋对结构整体刚度的贡献，从而造成计算模型的刚度略小于试验模型，进而导致计算模型的频率低于试验模型的自振频率。

图7 计算模型的前六阶振型

从图7可知，模型前两阶振型为平动，第三阶振型为整体扭转，第四、五、六阶振型为斗栱竖向振动。第一、二阶振型中的水平变形主要由柱架变形导致，同时斗栱层的侧向变形较小，这是因为斗栱层的侧向刚度要大于柱架的抗侧刚度，从而可以认为结构相对较容易发生破坏的位置主要在柱架处，这同时也和试验模型的倒塌机制一致，如图3a所示。

由以上分析可知，计算模型与课题组所做的试验模型在自振频率以及振型方面相吻合，说明两者的动力特性十分接近，因此计算模型可以代替试验模型进行结构动力反应时程分析。

2．2．2结构动力反应时程分析 在对结构进行不同工况下的加速度地震波的瞬态动力分析后，将不同节点的计算结果采用ANSYS程序提取出来。由于只在一个方向输入地震波，且有限元计算模型的结构布置均匀对称，因此不考虑结构扭转，标高相同处的加速度在水平方向上也大致相等，所以代表柱脚、柱架顶面及屋盖的测点可任意在柱底、柱顶及乳栿端的节点中进行选择。为验证所选取的有限元模型的准确性，通过对模型结构各位置地震响应进行分析，将得到的计算结果与图5试验模型在相同工况下的振动台模型试验结果[9]进行对比。选取兰州-50工况下屋盖加速度及相对位移反应进行对比，如图8所示。

(a) 加速度时程曲线 (b) 相对位移时程曲线

图8屋盖加速度及相对位移反应的计算值与试验值对比图

Fig.8Comparison of calculated values and test values for acceleration and relative displacement response of roof

由图8分析可得到，屋盖加速度反应和相对位移反应时程曲线的计算值与试验值吻合程度较高，到达峰值时刻也基本相同，说明所建立的模型单元一定程度上可以很好的模拟真实情况。其中存在的误差主要是因为试验模型在经过反复加载后结构阻尼有一定提高，以及榫卯节点和斗栱的恢复力滞回性能无法完全模拟，导致时程曲线相位偏差，但其误差在工程允许范围内。

2．3 地震波的选用

通过选取一组场地条件和反应谱特征不同的地震波(表2)来分析木结构古建筑在不同地震波作用下，其动力性能及抗倒塌能力所受的影响[18]，其中Ⅰ类、Ⅱ类、Ⅲ类及Ⅳ类场地分别选用的是迁安波、唐山波、Northridge波及天津波。为了分析木结构古建筑在长周期地震波作用下受到的影响，选取集集波与普通地震波进行对比。

表2 地震波的选取

注： PGA为峰值地面加速度(peak ground acceleration)。

为了分析结构地震反应在不同频率特性的地震动记录下的影响，对地震动记录进行反应谱分析得到峰值加速度及峰值位移与结构自身动力特性的相关关系，图9所列为阻尼比ξ=0.03[9]时各地震记录的标准加速度反应谱及位移反应谱。其中，将地震峰值加速度调整为同一值以便比较位移计算值的相对大小。

从图9a可以看出：在普通地震波中，Northridge波、唐山波及迁安波谱值的最大值在0～0.7 s之间；而天津波的加速度放大系数在1 s附近时明显较大，故在这个周期段内结构反应受天津波的影响较大。在1 s附近，结构谱加速度放大系数天津波>唐山波>Northridge波>迁安波。集集波谱值分布范围为0～4.5 s，比其他三个普通波宽，说明长周期建筑受到集集地震波影响较大。

从图9b可知，各地震波的位移谱值的差距在2 s之前很小，但集集波的位移谱值在2 s以后快速上升，并在4.2 s附近达到峰值。

(a) 标准加速度反应谱 (b) 位移反应谱

图9各地震波的反应谱

Fig.9Response spectrum of each seismic wave

2．4 基于IDA法的木结构古建筑抗倒塌性能研究

2．4．1不同工况下ANSYS计算结果 对所选地震波进行时间压缩及调幅，并将其依次输入到ANSYS程序中。通过非线性动力时程分析，得到缩尺模型在不同工况下的地震反应。按照倒塌破坏判定准则，倒塌指标选取柱脚最大滑移量xmax及柱架最大层间位移角θmax(表3和表4)，并通过IDA曲线图对不同地震动输入下木结构古建筑的抗倒塌性能进行分析比较。

表3 柱脚最大滑移量

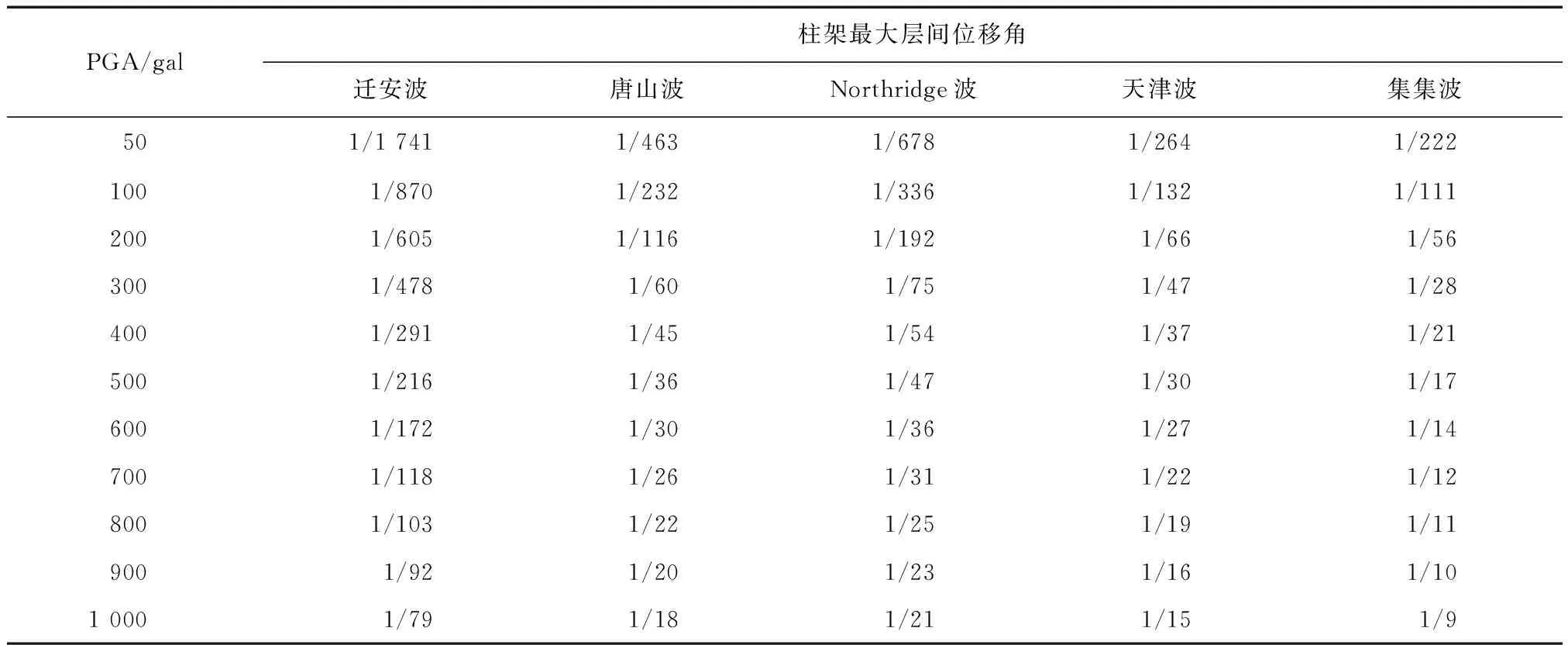
表4 柱架最大层间位移角

2．4．2柱脚滑移落架倒塌性能评估 当结构发生滑移落架时，应选择柱脚最大滑移量xmax作为倒塌性能评价指标，并以此绘制出不同地震动记录下的IDA曲线，如图10所示。图中的倒塌临界线为根据式(1)所得出的临界滑移量x=130 mm(对于试验模型，D=210 mm、t=25 mm)。

从图10可以看出，木结构古建筑柱脚滑移量在不同地震作用下有着明显区别：对于所选取的普通地震波，柱脚滑移量大小为天津波>唐山波>Northridge波>迁安波。而在集集波作用下的柱脚最大滑移量显然要比普通地震波大，表明木结构古建筑受到长周期地震波的动力影响程度要明显大于普通地震波。

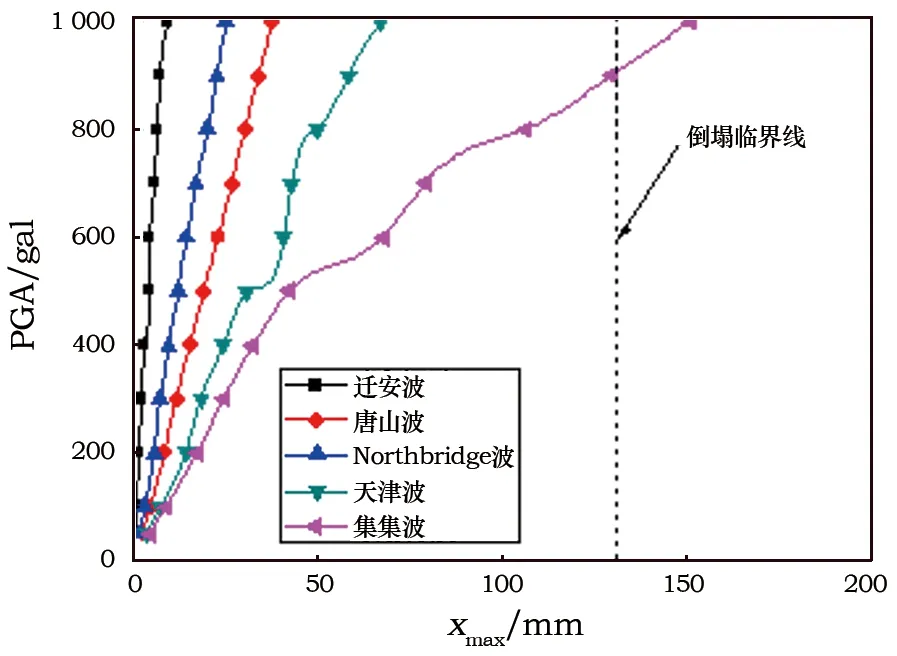
图10 柱脚最大滑移量的IDA曲线

2．4．3柱架层间倒塌性能评估 倒塌指标选取为柱架最大层间位移角θmax，并绘制出IDA曲线进行不同地震动作用差异分析，如图11所示。将层间倒塌的倒塌层间位移角临界值取为θ=1/20 rad。

从图11可知，当地震动强度大于一定数值时，结构就会因其自振周期与地震动的卓越周期相近，导致柱架侧移增大从而造成层间倒塌破坏。只是在长周期地震波作用下结构发生层间倒塌破坏所要达到的地震动强度较低，而在普通地震波作用下则需要较高的地震动强度。因此，长周期地震波对木结构古建筑层间倒塌破坏的影响要比普通地震波更大。

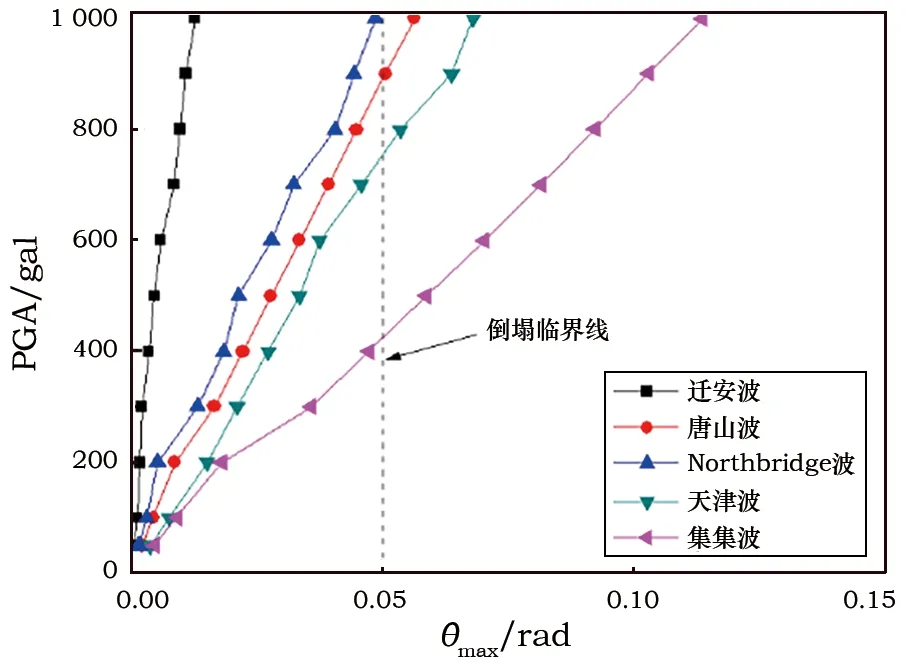
图11 柱架层间位移角的IDA曲线

2．4．4不同地震波作用下首次出现的倒塌机制 对图10和图11进行比较可知，结构在长周期地震波作用下，柱脚滑移破坏以及层间倒塌破坏这两种破坏机制都有可能发生。但是较先出现的倒塌机制才是导致结构产生倒塌的原因，因此就需要讨论不同情况下这两种破坏模式之间的优先次序问题。根据IDA曲线可知，所需地震动强度较小的倒塌机制最先出现，即“PGA最小原则”。当PGA>900 gal时，木结构房屋才会在长周期地震波作用下发生柱脚滑移倒塌破坏；而仅当PGA>400 gal时，木结构就会产生层间倒塌破坏。由此可知，层间倒塌破坏为长周期地震波作用下木结构古建筑首次出现的倒塌机制。

3 结 论

通过ANSYS软件对木结构古建筑的空间杆系模型进行了动力非线性分析，并采用IDA法对抗倒塌性能进行了研究，主要工作及结论如下。

1) 通过柱脚滑移倒塌的相对位移判定准则(式(1))及柱架层间倒塌的最大层间位移角判定准则(式(4))，得到了临界值的计算方法。

2) 木结构古建筑在普通地震波作用下不易出现柱脚滑移倒塌；层间倒塌为长周期地震波作用下最易出现的倒塌机制；相对于普通地震波而言，木结构古建筑受长周期地震波作用的影响更大。