基于小波包熵与AFSA-SVM的压力管道泄漏识别*

袁晶凤

(包头职业技术学院数控技术系 内蒙古包头 014030)

0 引言

随着环境气候保护意思的不断提升，天然气作为一种清洁能源得到了越来越广泛的使用，管道作为天然气的重要运输工具也随之进入了快速发展时期。随着管道使用年限延长，腐蚀、老化、恶劣的外界环境等因素在不断地破坏着管道壁的稳定性[1]。天然气管道泄漏引发的事故可能会严重影响人们的日常生活甚至危及生命、财产安全，对天然气管道的运行状态进行监测能有效地预防由泄漏引起的严重事故。

对于天然气管道的运行状态识别，许多学者提出不同的看法。王禾军等[2]运用经过混沌遗传算法优化后的SVM方法，用于检测油气管道运行过程中的TPD信号，有效提高了噪声与异常的分类精度并实现了对管道运行状态的精确诊断。王新颖等[3]提出了一种支持向量机与DS证据理论相结合的管道泄漏识别方法。该方法通过对SVM分类的结果进行二次DS数据融合，实验表明该方法有效提高了管道泄漏的识别率。王少锋等[4]在实验室的条件下，运用小波分析与声发射技术相结合的方法，对输气压力管道降噪与定位研究，成功实现了管道泄漏声发射信号主要频段的提取与泄漏源的精确定位。王建国等[5]针对管道泄漏声发射信号中混有大量干扰噪声而使得泄漏特征不易提取的问题，提出了运用小波包熵与EMD相结合的降噪方法。该方法有效地滤除了干扰噪声，提高了信噪比。QU Z等[6]提出了一种基于小波包能量特征与SVM相结合的管道泄漏检测方法，该方法能有效地检测管道异常振动的发生。

小波包分解是小波分解的进一步发展[7]。小波分解只对分析信号的低频部分进行分解，而小波包对低频、高频部分同时进行分解，从而提高了信号的时频分别率。小波包熵作为信息熵的演化能够准确反映节点信号携带的有用信息的多少。支持向量机理论(SVM)经过最近一段时期的发展被广泛应用于不同的领域，与传统的识别方法相比，泛化能力得到提高，计算结构被进一步优化。而人工鱼群算法(ASFA)作为一种新的智能算法，可以在初始参数不明确的情况下，进行全局寻优。本文将ASFA方法应用到SVM的核函数及惩罚参数选取过程中，提高了SVM的分类精度。

基于以上论述，运用小波包熵与AFSA-SVM相结合的方法对输气压力管道不同泄漏源进行模式识别的运算过程如下：

(1)特征向量提取：通过对泄漏声发射信号进行小波包分解，并以相关系数为准则对末层节点信号进行筛选。然后计算含有信息较多的节点信号的小波包熵值，获得管道泄漏的特征向量。

(2)参数优化：运用人工鱼群算法对SVM的惩罚因子、核函数参数进行全局优化，以提高SVM的泛化能力及分类准确率。

(3)SVM分类：将获得特征向量分为训练样本、测试样本两个部分，并分别输入到SVM分类器中，对压力管道不同泄漏模式进行识别。

1 小波包熵

小波包变换是分析非平稳信号的有效方法，其不仅可以提供更为精细的分解，而且可以自适应地把信号以二叉树原则分解到相匹配的频段内，提高了时频分辨率。其三层分解原理如图1所示。信息熵是一种常用的复杂信号不确定性的度量方法。熵值越大信息越不确定，反之熵值越小信息越稳定。信息熵理论与小波包分解相结合作为小波包熵，可以对故障信号能量变化进行定量分析。因此，可以用小波包熵对小波包分解各节点信号进行估计。

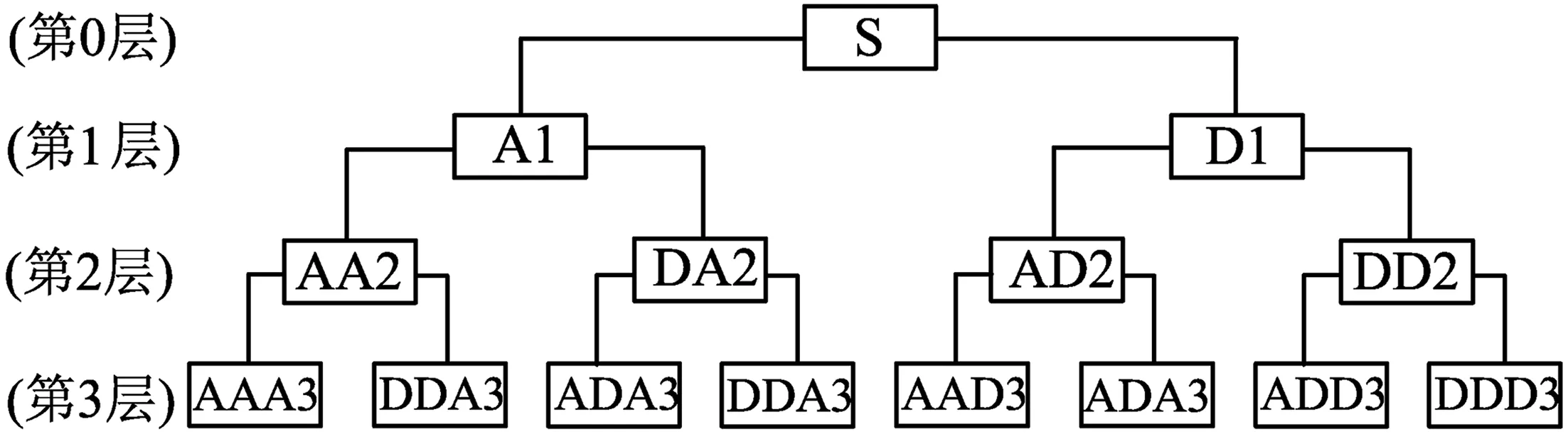
图1 小波包三层分解原理

根据信息熵理论，首先定义出代价函数对小波包分解后最后层各节点信号的特征进行刻画。假设包含以上各节点特征的向量x={xj}，则各节点的小波包熵为：

(1)

2 支持向量机及人工鱼群算法

支持向量机(SVM)是由Vapnik创建的统计学习理论发展而来[8～10]，是一种针对小样本分类和线性回归的机器学习方法。主要思想为，通过在并距离训练样本点距离较大的地方构造一个超平面作为决策曲面，使所有样本得到正确分类。

假设(xi,yi)作为训练样本，其中xi∈Rn为输入向量，yi∈R为输出向量。对于多分类支持向量机可以通过非线性变换将输入向量映射到高维空间，并在高维空间中求取最优决策曲面，实现样本的准确分类且间隔较大。为了求解位于高维空间中的决策曲面，构造线性分类函数：

g(x)=w·x+b

(2)

式中，w为权向量；b为分类阈值。根据结构风险最小化原理，可以将分类问题转化为如下的优化问题：

约束条件为：

(4)

其中，C为惩罚因子被用来调节对误分类样本的惩罚程度；ξ为松弛系数用来表示被误分类的样本数。

进一步转化为对偶化问题：

约束条件为:

有此可以得到最优分类函数：

SVM分类器常用的核函数分别为线性核函数、多项式核函数、径向基(RBF)核函数以及Sigmoid核函数。其中RBF核函数可以将待分析样本映射到更高维的空间，并可以处理非线性对应关系，因此本文中的SVM分类器选择了径向基核函数，其表达式为：

k(xi,yj)=exp(-|xi-xj|/σ2) (8)

人工鱼群算法(AFSA)是一种新的高效仿生优化算法，具有比较强的全局寻优能力。该方法通过模拟多条人工鱼的觅食、聚群、追尾以及与之相关的随机行为，通过不断调整人工鱼的参数，能够比较迅速地收敛在最优值附近，从而实现全局寻优[11-12]。运用AFSA对SVM的惩罚参数C以及核函数参数g进行全局寻优，可以提高支持向量机的泛化能力与分类准确率，有效避免了盲目选取参数造成的随机误差，其优化流程如图2所示。

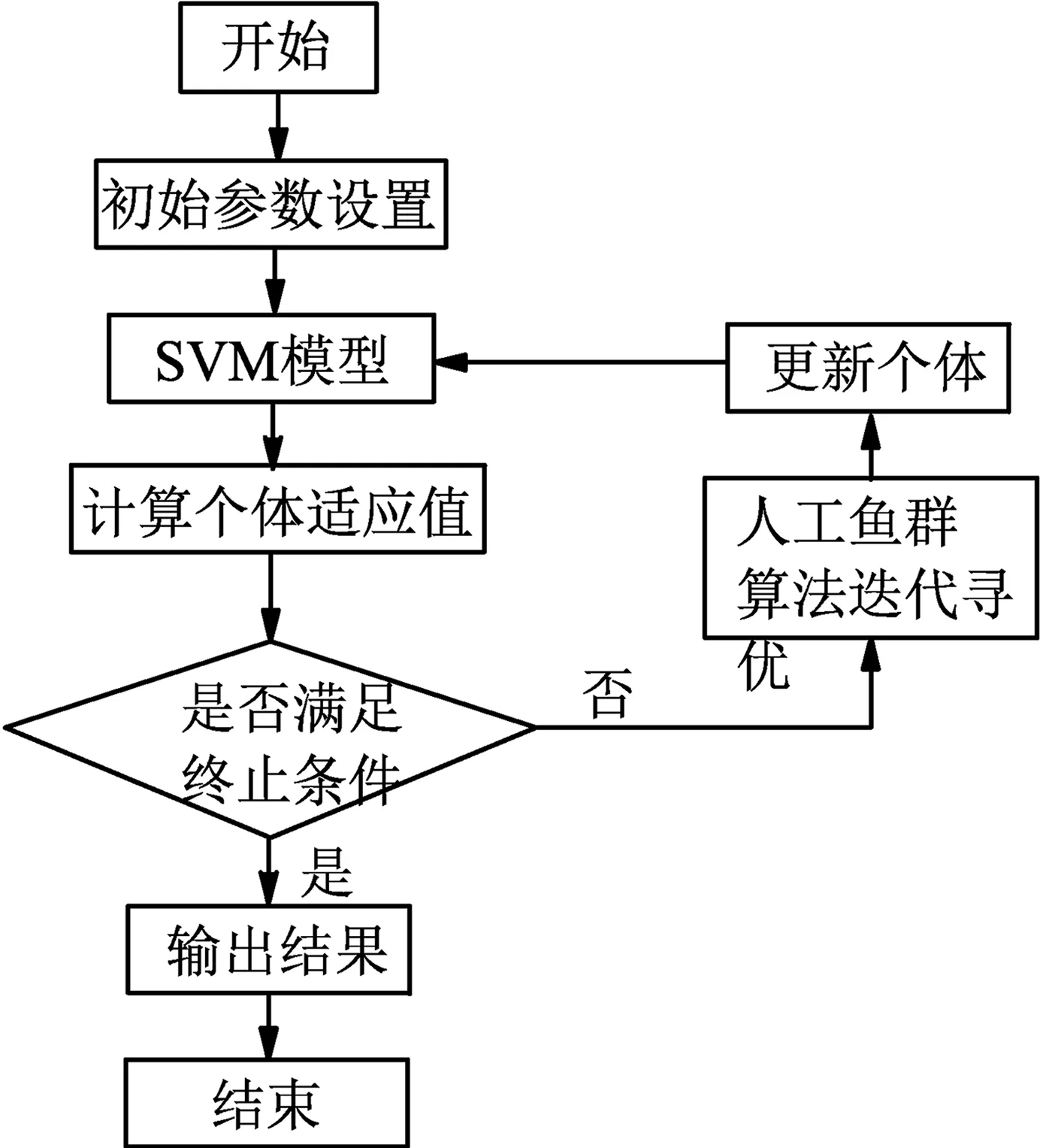
图2 运用AFSA优化SVM参数流程

3 实验结果与分析

3.1 实验设置及信号采集

为模拟天然气管道泄漏，本实验采用长度5.6 m、壁厚为8 mm的不锈钢管道作为实验对象，气体压力设置为0.4 MPa，并在管道中部设置泄漏源，泄漏孔径设置为1 mm、2 mm、3 mm、5 mm。实验示意如图3所示。对于泄漏产生的声发射信号采用美国PAC公司生产的声发射采集系统，其中传感器采用R15声发射传感器，门限值设置为30 dB，前置放大倍数为40 dB，采集4种不同泄漏的声发射信号波形。

对应4种泄漏孔径的泄漏连续时域波形：横坐标时间0～1 000 μs,纵坐标幅值-0.1 mV～0.1 mV。泄漏孔径1 mm 和2 mm的时域波形相似，泄漏孔径3 mm和4 mm的时域波形相似。

图3 实验示意

为了方便讨论，以1mm泄漏源产生的声发射信号为例进行管道泄漏信号特征向量提取。首先根据经验采用db4小波基，对泄漏声发射信号进行3层小波包分解，其第三层各节点重构信号的时域波形可以看出第5～8节点信号幅值比较低，说明这些节点信号中主要包含的是干扰噪声，而 (3,0)、(3,1)、(3,3)节点信号具有明显的管道泄漏声发射信号特征。由于相关系数可以反映节点信号与原信号的相似程度，可以将相关系数作为节点信号含有有用信息多少的准则。为了进一步选取敏感的节点信号，对比第三层各个节点重构信号与原始信号的相关系数，可以发现节点(3,2)，(3,4)～(3,7)重构信号的相关系数都位于0.13以下，为了进一步提高SVM分类运算效率，因此选择节点(3,0)、(3,1)、(3,3)作为敏感节点信号，并计算其小波包熵值作为特征向量，输入SVM进行分类运算。运用同样的方法可以得到其余泄漏信号对应敏感节点信号的小波包熵值，对4种不同的泄漏源分别进行了10组实验，其中第1组实验中不同泄漏信号的小波包熵值如表1所示。

1 mm泄漏源泄漏声发射信号3层小波分解的第三层各节点重构信号的时域波形：横坐标时间0～1 000 μs,纵坐标幅值-0.05 mV～0.05 mV。波形前4个节点幅值波动大，明显有幅值变化在-0.05 mV～0.05 mV之间，5～8节点幅值波动小，幅值不明显。

第三层各节点相关系数二维柱形图： 以0.13纵坐标为界，(3.0)相关系数0.4左右，(3.1)相关系数0.7左右，(3.3)相关系数0.6左右。

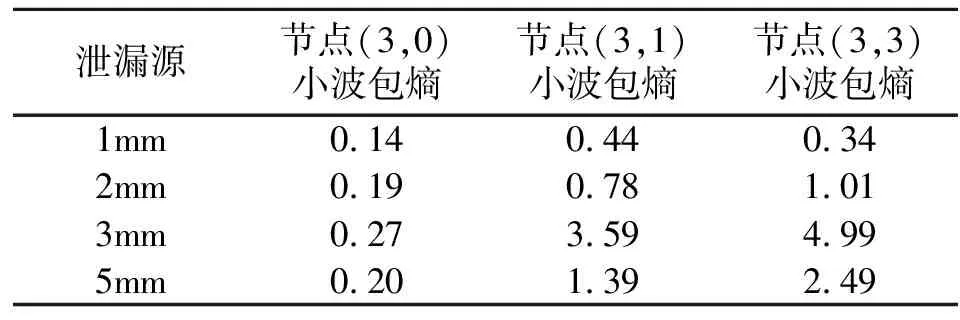
表1 不同孔径泄漏信号小波包熵值

3.2 基于AFSA-SVM的泄漏特征识别

首先对人工鱼群参数进行初始设置，其中人工鱼群数量为40，最大迭代次数设置为20，视觉范围为10，移动步长为1.25，拥挤度因子xx，当算法达到最大迭代次数时终止寻优。从寻优适应度曲线可以看出，进化到第1代时就已经搜索到最优值，并保持不变，此时得到最优惩罚参数C=50.09,核函数g=0.253。

在压力管道不同泄漏的10组实验中，随机选择6组实验数据作为训练样本，余下的4组实验数据作为测试样本。将优化后的参数代入到SVM分类器中，得到识别结果可以看出4组测试样本数据的分类结果与实际类别一致。

人工鱼群算法参数寻优适应度曲线：横坐标进化代数0～20，纵坐标识别率94.5%～97%。横坐标1～20进化，寻优适应度曲线是识别率95.5%～96%的直线。

AFSA-SVM泄漏分类测试结果：横坐标测试样本，纵坐标类别标签。4种泄漏的每4组测试样本：红色实测类别全部贴合蓝色预测类别。

4 结论

(1)压力管道泄漏产生的声发射信号中包含了泄漏源的特征，通过对管道泄漏信号进行分析，能有效地提取泄漏源的本质特征，提高了管道检测效率。

(2)小波包分解与相关系数相结合的方法能有效地选取末层敏感节点重构信号，并通过小波包熵值计算有效提取管道泄漏信号的特征向量。

(3)通过AFSA能有效地优化支持向量机的核函数参数与惩罚因子，提高了SVM的分类准确率，为SVM参数优化提出了一种新方法。