基于内聚力单元的弹性涂层多颗粒冲蚀机理

徐建新，朱晓红，郭巧荣，李顶河

（中国民航大学航空工程学院，天津 300300）

材料冲蚀现象是航空器材料破坏的主要原因之一。涂层技术便于实施，可有效提高飞机零部件抗冲蚀能力。在基体材料表面沉积一层抗冲蚀性能好的涂层，可降低粒子对材料的冲蚀量[1]。研究涂层的抗冲蚀性能，对涂层抗冲蚀损伤能力进行合理的分析与评估具有工程意义。

自1958 年Finnie 微切削理论问世以来，学者们根据各自试验结果建立了不同的冲蚀理论，力图解释或预测材料的冲蚀行为[2]。但由于材料的自身属性（内在因素）和冲蚀条件（外在因素），使得冲蚀现象复杂多变，现有理论均存在局限性。Griffin 等[3]建立了5 颗粒冲蚀模型，直观地看到了基材的受损情况。张伟等[4]采用自主研发的冲蚀磨损试验机，以碳素钢为参照，对碳化硅陶瓷进行了冲蚀磨损实验。吕东莉等[5]模拟了石英砂对20#钢的冲蚀动力学行为，获得了冲击角度、速度及粒径变化对冲蚀过程应力分布的影响规律。目前对冲蚀问题的研究，一般假设涂层/基体紧密接触，或仅对涂层建模，忽略了连接涂层与基体的胶层带来的影响。

针对以上问题，考虑涂层与基体的结合性能，基于内聚力单元建立了多颗粒冲蚀模型，研究了弹性涂层在颗粒冲蚀下的影响，为正确理解弹性涂层的冲蚀机理以及寿命预测提供了参考，也为飞机零部件弹性涂层的设计、优化以及服役后的维护和修理提供了理论依据。

1 基于内聚力单元的冲蚀模型

1.1 内聚力单元

基于双线性牵引分离（T-S）法的内聚力单元本构方程，可有效模拟涂层的分层失效[6-7]。内聚力单元损伤原理的双线性本构模型如图1所示。

图1 内聚力双线性本构模型Fig.1 Bilinear constitutive model of cohesion

图1 中所示双线性本构响应可表示为

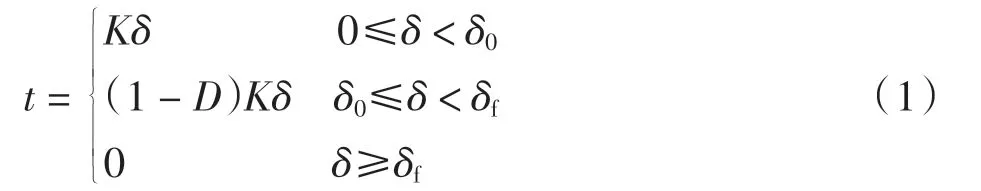
其中：t为界面分离牵引应力；δ为分离位移；δ0为损伤开始时的临界位移；δf为单元完全失效时的位移；K为初始界面刚度；D为内聚力累积损伤刚度（初始值为0，表示材料没有屈服或者是刚刚屈服；当D=1 时，表示材料失去承载能力）。

采用最大应力判据准则确定材料损伤起始临界点，即

其中：tn，ts和tτ分别表示法向n和两个切向s和τ 上的应力分量；tn0，ts0和tτ0分别为法向n 拉伸强度和两个切向s和τ 上的切向强度；〈〉为Macaulay 算子，其表达式为

采用幂函数损伤准则评价混合模式下的粘结面过程[8]，其表达式为

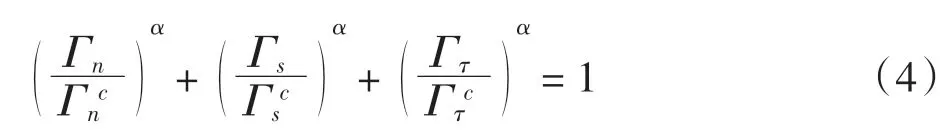
其中：Γn，Γs和Γτ分别为法向应力和两个切向应力所做的功。根据文献[9]，选用最普遍的α=1。

1.2 有限元模型

利用有限元方法建立颗粒冲蚀涂层的二维对称模型，如图2所示，其中：a为压头与涂层的接触半宽；R为压头半径；L为系统半宽；hs为基体厚度；hc为涂层厚度；hb为粘结层厚度。

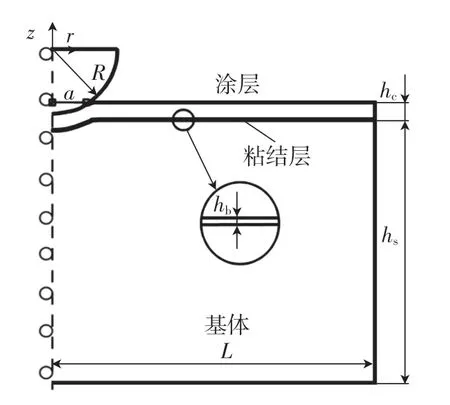
图2 颗粒冲蚀力学模型Fig.2 Mechanical model of particle erosion

模型中颗粒的硬度远大于涂层的硬度，将颗粒视为简单的刚体。涂层-基体系统半宽L=200 μm，涂层和基体的单元类型为平面应变单元，网格细分如图3所示。模型参数如表1所示，基体屈服应力为1 000 MPa。

图3 有限元网格细分示意图Fig.3 Finite element mesh subdivision diagram

表1 有限元模型基本参数Tab.1 Basic parameters of finite element model

1.3 有限元模型的验证

定义半径为R=50 μm的球形压头，指定位移h=2 μm。绘制涂层表面径向应力和粘结层切向应力的分布图，并与文献[9]结果进行对比，如图4和图5所示。可以看出，仿真结果与参考文献拟合良好，证明所建有限元模型具有较高的可信度。

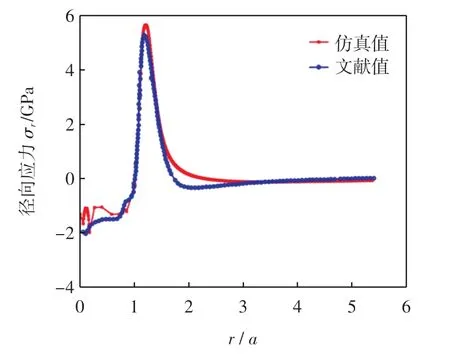
图4 涂层径向应力分布对比Fig.4 Radial stress distribution comparison of coating

图5 粘结层切向应力分布对比Fig.5 Shear stress distribution comparison of adhesive layer

2 分析与讨论

颗粒冲蚀涂层时，可能存在散布式和集束式颗粒流冲蚀两大类，如图6所示。

图6 冲蚀方式分类Fig.6 Erosion patterns

从几何角度来讲，冲蚀效应可具体化为冲蚀密度、冲蚀距离和冲蚀次数对涂层性能的影响。将颗粒形状简化为球形，建立二维多颗粒冲蚀对称模型，曲线图均取中心轴右侧建立坐标系。

2.1 冲蚀密度的影响

颗粒半径均设置为10 μm，在同一涂层区域，分别有1～4个颗粒进行冲蚀，如图7所示。不同冲蚀密度下的应力分布如图8所示。

图7 冲蚀密度示意图Fig.7 Schematic diagram of erosion density

图8（a）给出了涂层表面的径向应力分布曲线。最大拉应力在接触半宽附近，以单颗粒球为例，在r≈1.2 a 处；而压应力分布在r ＜a的区域内。随着冲蚀密度的增加，拉应力和压应力峰值位置逐渐右移，但始终在最外侧颗粒处。从拉应力的极值点可以看出，左侧极值点处的极值小于最右侧边缘处的极值，可知在冲蚀密度增大的情况下，颗粒之间的相互作用并没有使涂层表面单个颗粒接触边缘的拉应力增大，反而减小。统计1～4个颗粒的拉应力最值，即图8（a）中最右侧的极值，也就是边缘颗粒的最大拉应力，分别为8.041 GPa、7.201 GPa、6.897 GPa、6.756 GPa，可知冲蚀密度越大，涂层表面所受到的最大拉应力越小。

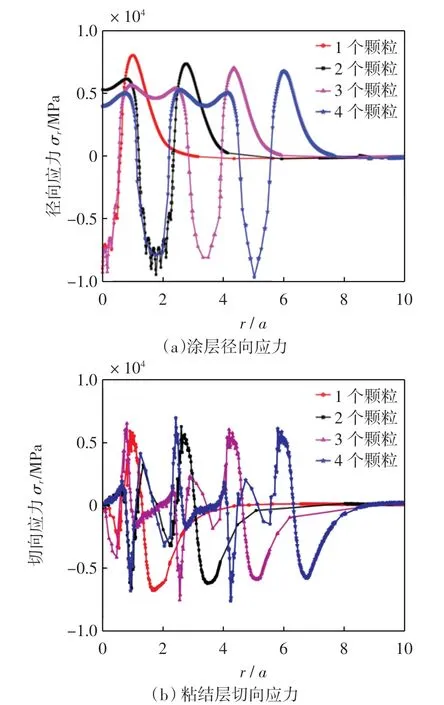
图8 不同冲蚀密度下的应力分布Fig.8 Stress distribution under different erosion densities

图8（b）给出了粘结层切向应力分布。相对于法向应力，切向应力在涂层-基体界面的分层中占主导[10]，故只讨论切向应力的影响，不考虑其中的压应力（负值）[11]。对于多颗粒来讲，以每个颗粒中心点为原点，在r≈1.2 a处，切向应力很大；并且密度大，颗粒之间的相互作用使切向应力剧烈变化，最大切向应力随之变大，导致界面分层萌生于密度较大的区域。

2.2 颗粒间距的影响

对于冲蚀密度小的颗粒冲蚀，研究颗粒间距对冲蚀效果的影响。为方便描述，取典型冲蚀模型进行分析，如图9所示。

图9 冲蚀距离示意图Fig.9 Schematic diagram of erosion distance

以图9 中半球形颗粒的圆心O1和O2为参考点，分别取O1O2=d，2d，3d 进行应力对比分析，如图10所示。以单颗粒情况作参考，选取横坐标的位置与其他3个不同，不考虑其相位差。颗粒距离较近时，涂层表面最大拉应力受相邻颗粒的影响较大，颗粒接触中心左侧极值明显小于右侧极值；粘结层切向应力受相邻颗粒影响，使颗粒左侧拉应力的峰值明显变小。随着颗粒距离增大，如O1O2≥2d 时，以颗粒接触中心为对称点，涂层左右侧径向应力极值趋于相等，应力曲线呈对称分布，与单颗粒冲蚀分布一致；粘结层切向应力在涂层表面的趋势以及大小也与单颗粒对应相同。总之，随着颗粒冲蚀的距离增加，颗粒之间的影响逐渐减小，当O1O2≥2d 时，颗粒冲蚀对涂层裂纹和分层的产生不会有叠加影响。

2.3 多次冲蚀的累积效应

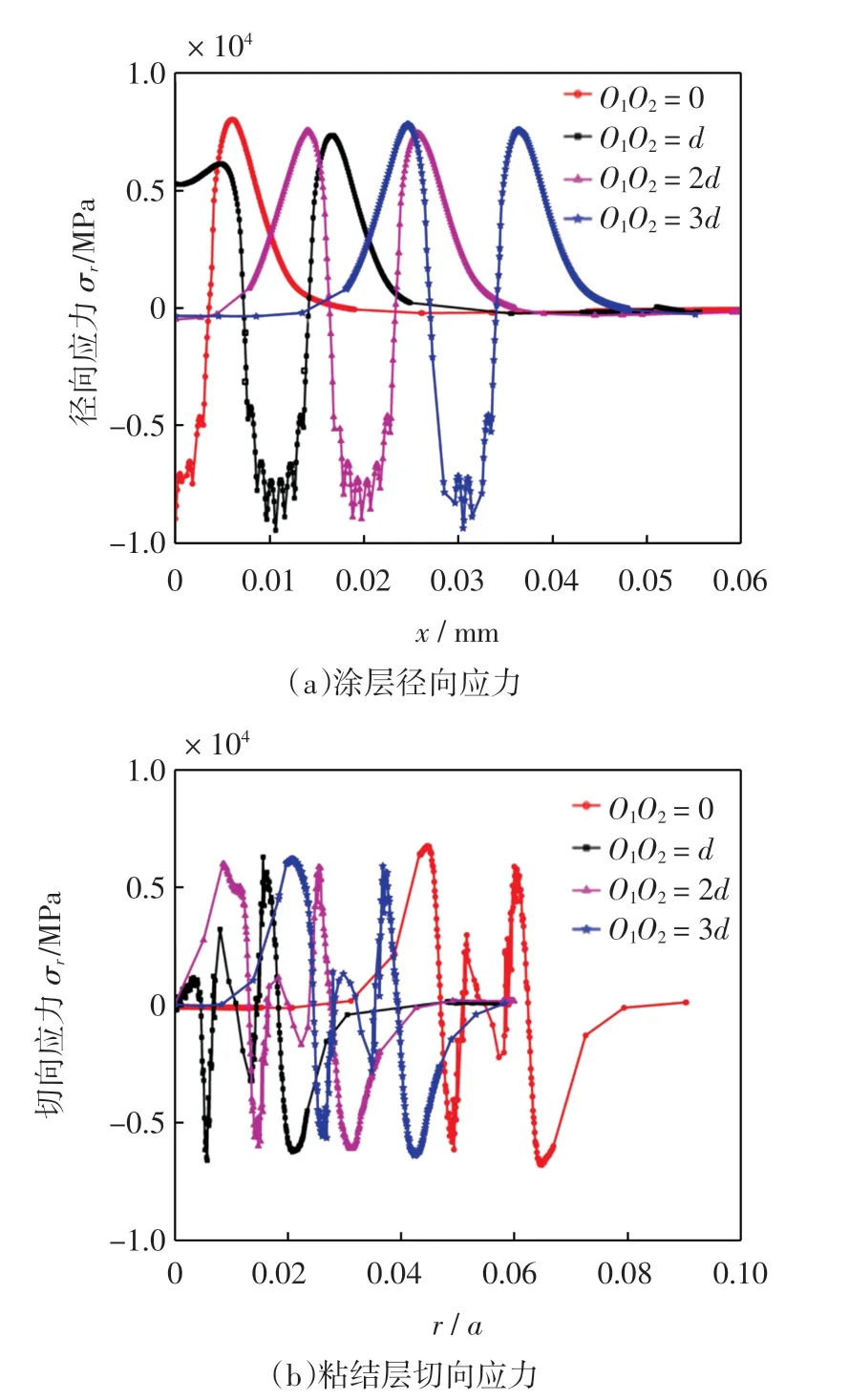
图10 不同颗粒距离下的应力分布Fig.10 Stress distribution under different particle distances

为研究颗粒多次冲蚀的累积效应，对同一涂层位置反复冲蚀，冲蚀5 次后产生2 μm 深的凹坑。冲蚀5次后的曲线和单次冲蚀后的曲线进行对比，如图11所示。从图11（a）可以看出，涂层在冲蚀起始产生比较浅的凹坑时，径向最大接触应力位于表面的接触中心处，为压应力。在多次冲蚀完成后，涂层径向的最大接触应力位于表面的接触边缘处，为拉应力。在整个冲蚀累积过程中，拉应力的峰值在接触边缘处几乎呈线性增加。另外，涂层径向应力沿表面水平方向由压应力迅速突变为拉应力，压、拉应力的突变随冲蚀次数的增加越来越剧烈。从图11（b）可以看出，在整个冲蚀累积过程中，粘结层的切向应力峰值在接触边缘比较稳定。粘结层切向应力沿界面水平方向由拉应力迅速突变为压应力，由于冲蚀累积过程中压应力的变化较大，拉、压应力的突变随着冲蚀次数的增加也愈加剧烈。拉、压应力突变会形成交变应力，是导致弹性涂层失效的主要原因。

另外，多次冲蚀后产生2 μm 凹坑时的最大径向应力比单次冲蚀后的值小，且应力曲线存在相位差，最大值更加靠近接触边缘，约在r=1.05a 处；对于粘结层，两者最大切向应力峰值相同，曲线存在相位差，切向应力最大值靠近接触边缘，约在r=1.05a处。综上，多次冲蚀后涂层裂纹萌生的位置更加靠近接触边缘，与单次冲蚀约存在0.15a的相位差，涂层表面与粘结层的应力曲线产生同相位的平移，可见分层与裂纹萌生的位置更加靠近接触边缘，且分层与裂纹相互影响。

图11 不同冲蚀次数应力分布Fig.11 Stress distribution under different erosion times

3 结语

1）在产生同样凹坑深度的情况下，冲蚀密度越大，涂层表面所受最大拉应力越小，粘结层剪应力变化越剧烈；涂层裂纹萌生于涂层表面最外侧接触边缘处，界面分层萌生于密度较大接触区域边缘处。

2）当颗粒距离较小时，涂层在颗粒相邻侧的拉应力比外边缘处小，粘结层在相邻侧的切向应力也变小。随着颗粒冲蚀距离的增加，颗粒之间的影响会减小，当距离大于2 倍球心距时，颗粒之间不会产生影响。

3）随着冲蚀次数的增加，涂层与粘结层拉、压应力的突变越来越剧烈。与产生相同凹坑深度的单次冲蚀相比，多次冲蚀在涂层表面产生的最大径向应力更小，峰值出现的位置更加接近接触边缘；涂层表面径向应力和粘结层剪应力与一次冲蚀相比均存在应力相位差，且差值相同。

以上结论可为研究复杂的服役环境下航空发动机的涡轮和压气机叶片的热障涂层冲蚀失效提供理论参考。