漠河地区多年冻土地基温度场附面层参数研究

戚春香，李 瑶，马 琳，董 彬

（中国民航大学机场学院，天津 300300）

根据中国机场建设规划，东北地区将开展大量的机场建设以及改扩建工作，其中包括大小兴安岭机场群的建设。大小兴安岭地区分布有大面积的高纬度冻土，而目前对于冻土地基的研究主要集中于极地地区及中国青藏高原地区。Goering 等[1]对片块石冻土路基温度场进行了数值模拟；Andrew[2]研究了加拿大北极地区多年冻土地基温度场状况；Kudriavtcev 等[3]分析了俄罗斯冻土区铁路路基温度场的分布。由于温度场上边界条件复杂多变，建立模型时有诸多不便，朱林楠[4]基于青藏公路实测地基温度提出了附面层理论，用稳定的附面层代替了温度场复杂的上边界条件，在多年冻土区温度场研究中得到日益广泛的应用；金龙等[5]根据青藏高原地基温度资料及附面层原理，将青藏公路典型路基温度场模型上边界条件表示为温度函数；刘伟[6]应用青藏高原附面层理论分析了黑色宽幅路基温度场规律；曹元兵等[7]应用附面层理论建立了玛多地区多年冻土地基温度场模型；白青波[8]根据西部地区主要路段地基温度日波动状况自定义了附面层厚度的选取标准，并根据该标准探究了附面层厚度及温度增量的取值。杨简[9]应用附面层理论建立了青藏高原多年冻土区机场跑道的温度场模型。

大小兴安岭地区气候环境及地基温度状况都与青藏高原不同，青藏高原多年冻土环境及地基温度状况确定的附面层理论参数是否适用于东北地区多年冻土地区还需深入研究，为此选取中国目前唯一已进行机场建设的多年冻土区——漠河作为研究对象，利用ABAQUS 建立漠河地区机场跑道多年冻土地基温度场模型，以确定漠河地区附面层理论参数取值，为东北地区多年冻土区机场跑道建设提供理论基础。

1 有限元模型

1.1 地基温度场模型结构

采用二维对称模型，DCAX8 计算单元，其1/2 结构如图1所示。整体模型道面板总宽为60 m，两侧道肩宽度为40 m，此宽度可忽略边界效应的影响[9-10]，土体厚度取40 m。

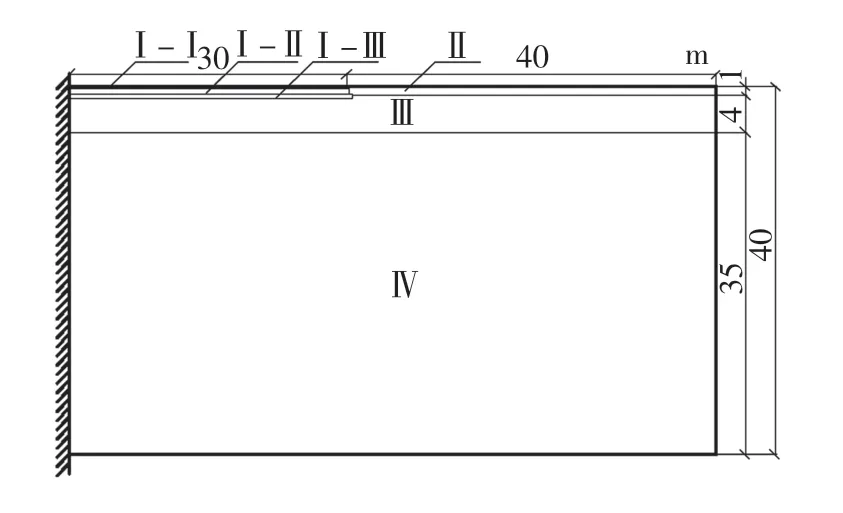
图1 地基温度场模型Fig.1 Foundation temperature field model

Ⅰ区为道面结构层，根据《民用机场沥青道面设计规范》[11]的相关规定，其组成如表1所示。道面结构总厚度为1.4 m，满足最小防冻层厚度要求[11]。Ⅱ、Ⅲ、Ⅳ区为土层结构，Ⅱ区为1 m 厚亚粘土层（35%含水量），Ⅲ区为4 m 厚亚粘土层（15%含水量），Ⅳ区为35 m 厚碎石亚粘土层。

表1 道面结构层Tab.1 Pavement structure layers

1.2 热参数

由于水分迁移的影响，模型Ⅱ、Ⅲ、Ⅳ区土层热参数应采用等效比热容c（T）和等效导热系数[10]λ（T），分别为

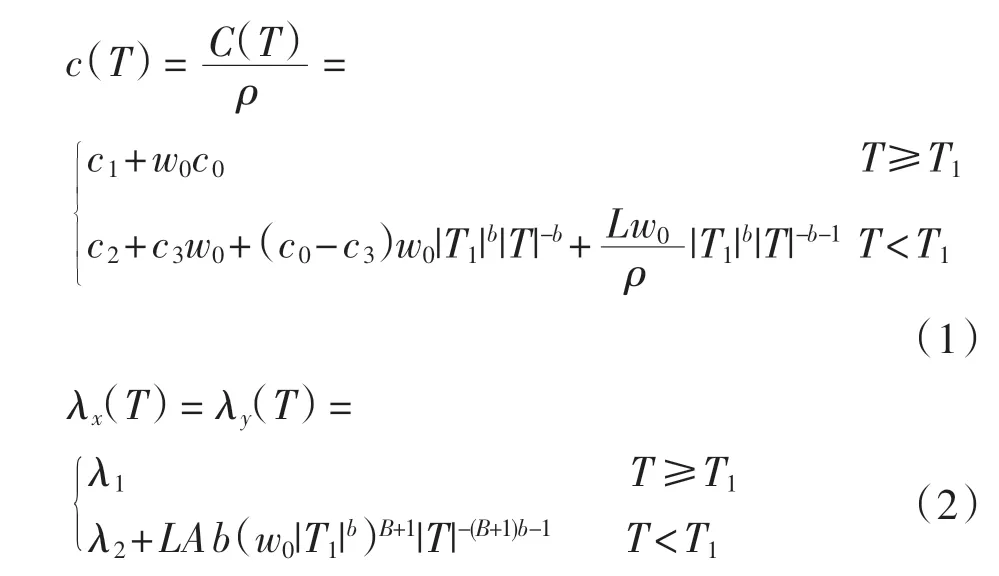
其中：T为地基温度（℃）；C（T）为体积热容量；ρ为土体干密度（kg·m-3）；c1、c2分别为融土和冻土的比热容（J·kg-1·℃-1）；w0为初始含水率（%）；c0、c3分别为水和冰的比热容，c0=4 182 J·kg-1·℃-1，c3=2 090 J·kg-1·℃-1；T1为土体冻结温度（℃）；A、B、b为经验系数，A = 2.3 521，B=3.2 659，b与土质有关，可通过试验测得；L为水的相变潜热，L=334 560 J·kg-1；λx（T）、λy（T）分别为横向和纵向等效导热系数，λ1、λ2分别为融土和冻土的导热系数（W·m-1·℃-1）。

各参数取值如表2、表3所示[12-14]，在ABAQUS 中利用Fortran 语言编写UMATHT 子程序。

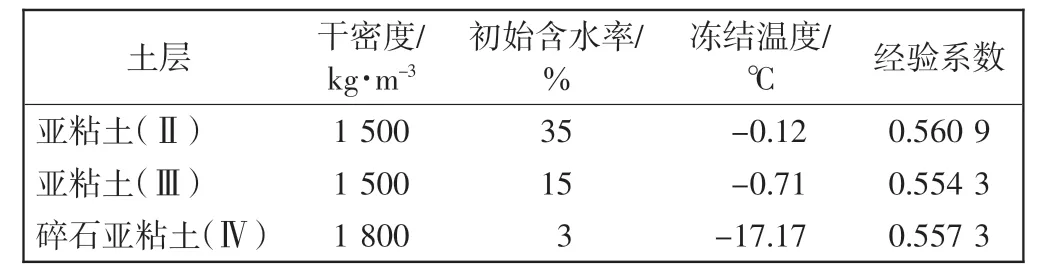
表2 土层基本参数Tab.2 Basic parameters of soil layers

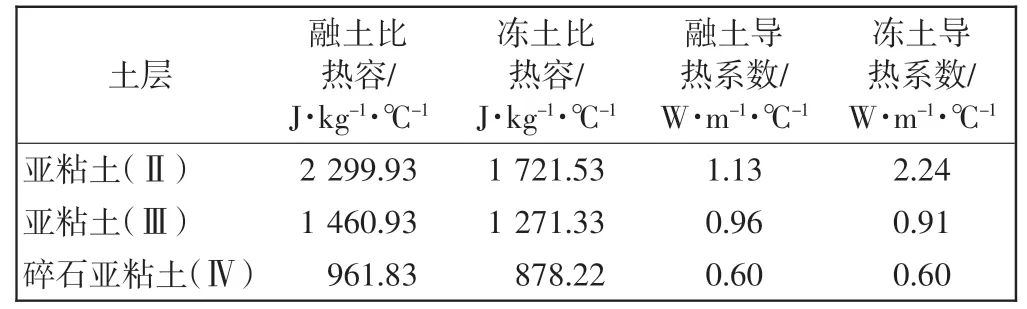
表3 土层热参数Tab.3 Thermal parameters of soil layers

模型Ⅰ区为道面结构层，由于其保水性差可忽略水分迁移，因此无需采用等效热参数，其各层热参数如表4所示[10，15]。

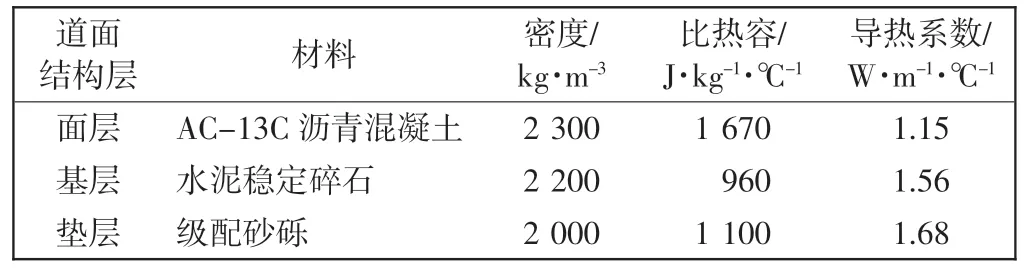
表4 道面结构层参数Tab.4 Parameters of pavement structure layers

1.3 边界条件

由于附面层理论是基于上边界条件的研究，因此只考虑模型上边界条件的施加，利用广泛采用的综合考虑第二类、第三类上边界条件，在ABAQUS 中分别定义模型上边界的蒸发耗热、对流换热条件以及太阳辐射条件。

研究[15]表明：沥青混凝土道面的蒸发耗热小于太阳辐射的5%～10%，对地基影响相对很小；同时天然地表在冻结状态几乎没有蒸发耗热。因此，在计算地基温度场时可忽略蒸发耗热的影响。

1）对流换热条件

道面与大气之间的对流换热主要与气温及两者之间的对流换热系数有关，通过FILM 子程序定义气温函数以及各月对流换热系数即可实现对流换热条件的定义。根据中国气象数据网的资料，漠河地区1981—2010 年各月平均气温如表5所示。

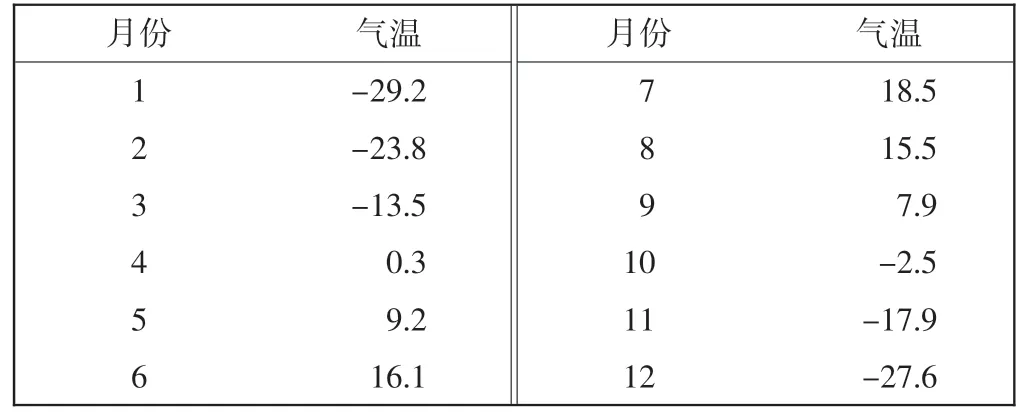
表5 漠河地区各月气温Tab.5 Monthly atmospheric temperature in Mohe district ℃

考虑0.05 ℃/年的升温效应，则漠河地区月平均气温为

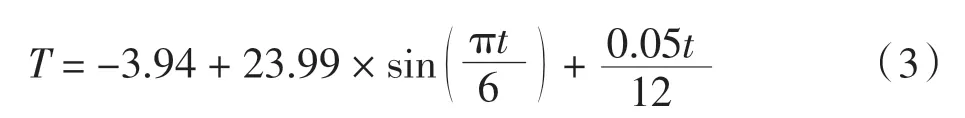
其中：t为时间（月），t=0 时为4 月。

研究[16]表明：地表与大气间的对流换热系数h 主要受风速的影响，其表达式为

其中：vw为平均风速（m·s-1）。

将中国气象数据网提供的漠河地区1981—2010年各月平均风速代入式（4）可得其各月对流换热系数，如表6所示。

表6 对流换热系数Tab.6 Convective heat transfer coefficient W·m-·2℃-1

2）太阳辐射条件

太阳净辐射为吸收的太阳总辐射与地面有效辐射的差值，模拟时应用DFLUX 子程序定义各月太阳总辐射，如表7所示。同时定义太阳辐射吸收率和沥青混凝土面层太阳辐射吸收率为0.87，天然地面太阳辐射吸收率为0.71。

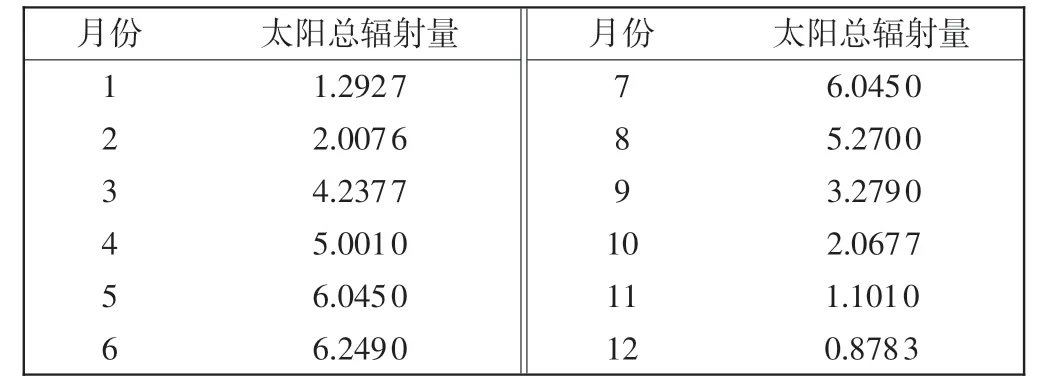
表7 各月太阳总辐射量Tab.7 Monthly total solar radiation 108 J·m-2

在ABAQUS 中通过定义气温幅值曲线，同时在Edit Attributes 中定义Stefan-Boltzmann 常数以及绝对零度值，可实现地面有效辐射的定义，即

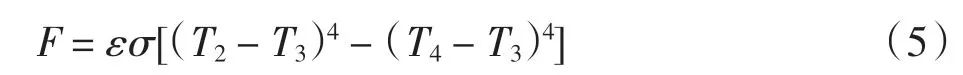
其中：ε为发射率（黑度）；σ为Stefan-Boltzmann 常数，σ=5.669 7×10-8W·m-2·K-4；T2为地表温度（℃）；T3为绝对零度值，T3=273.15 ℃；T4为大气温度（℃）。

1.4 计算分析步

采用Heat transfer 瞬态分析步，计算时长以月为单位，总时长设为240，步长设为1，即模型共计算20年，每步计算时长为1个月，共需计算240 步。

2 漠河地区附面层参数分析

2.1 附面层理论

根据相关文献[5-9]，对于多年冻土区地基温度场模型，上边界可由厚度为H的附面层代替，上边界条件可用附面层底温度函数表示，即

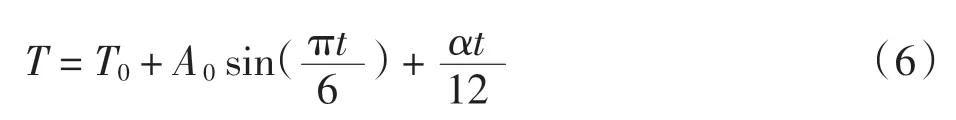
其中：T为地基温度（℃）；T0为附面层底地基温度初始值（℃）；A0为附面层底地基温度振幅（℃）；t为计算时间（月），t=0 时代表第1 年4 月；α为大气温度升温速率，取α=0.05 ℃·a-1。

2.2 参数分析

由式（6）可知，附面层参数为附面层厚度H 及附面层底地基温度初始值T0、振幅A0。提取漠河地区温度场数值，利用OriginPro 9 软件对地基温度数据进行处理分析。

1）提取数据

根据相关资料，附面层通常位于道面结构中，模型道面结构总厚度为1.4 m，因此分别提取沥青混凝土道面和天然平整地面地基0～2 m 深度内的温度，每隔0.1 m 提取1 组数据，共40 组。为避免沥青混凝土道面与天然平整地面地基温度之间的相互影响，提取数据时根据温度场提取等温线近似直线处的地基温度，分别提取了模型左、右边界处地基温度代表沥青混凝土道面、天然平整地面下部地基温度。

2）编写函数

在OriginPro 9 软件中打开Fitting Function Organizer 编辑式（6）所示函数，参数为T0、A0，在Parameter Setting 中将其Value 值均设为1。

3）确定参数

将沥青混凝土道面地基0～2 m 深度内共21 组沿时间变化的地基温度数据导入OriginPro 9 中，利用所编写函数分别对每一组数据进行拟合，其中时间为自变量，地基温度为因变量。比较21 组数据的拟合度，找出拟合度最高的两组数据，如图2（a）所示，拟合度最高的为深度0.1 m与0.2 m 处的地基温度。

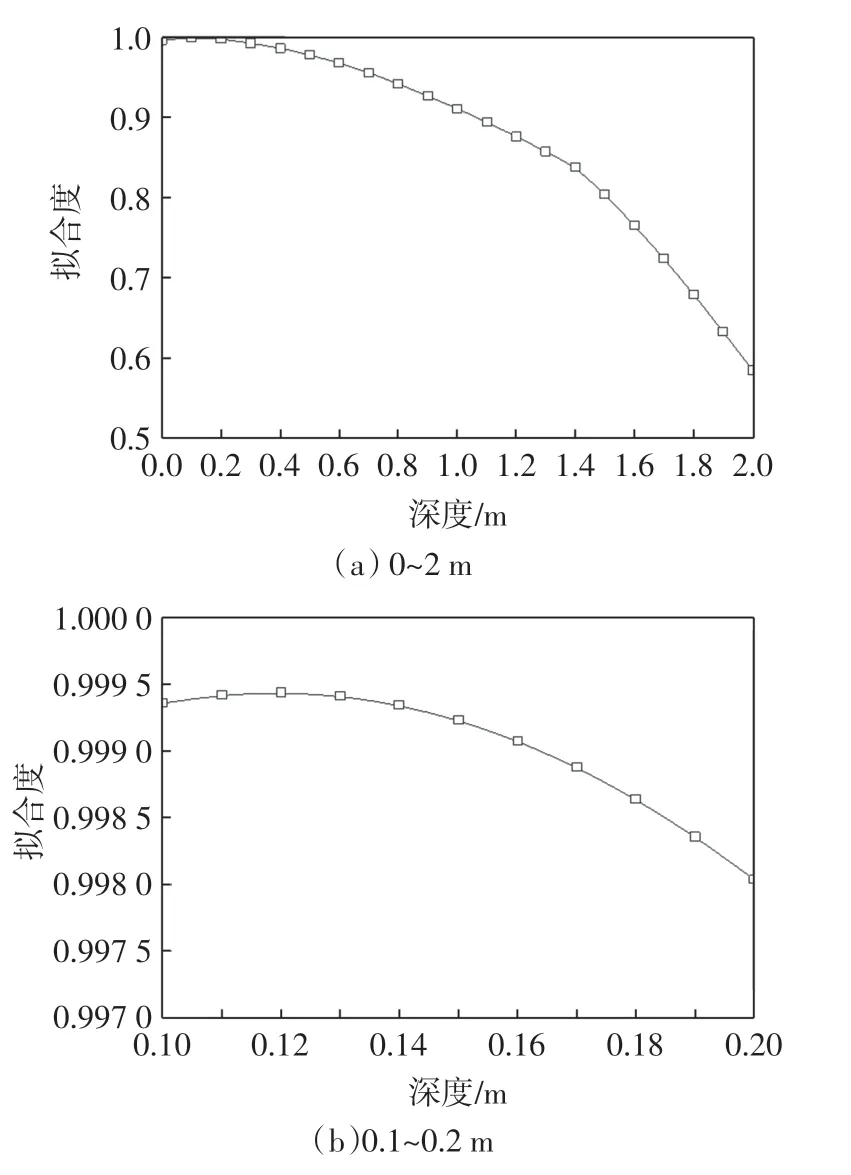
图2 不同深度处的地基温度拟合度Fig.2 Fitting degree of ground temperature at different depths

以0.01 m为单位提取沥青混凝土道面地基0.1～0.2 m 深度内共11 组温度随时间变化的数据，比较其拟合度，如图2（b）所示，深度0.12 m 处的地基温度拟合度最高，附面层厚度即为0.12 m，拟合函数的参数T0、A0即为附面层底温度函数的参数T0、A0，如表8所示。

同理，由天然平整地面地基0～2 m 深度内温度随时间变化的数据亦可得到其对应的附面层参数，如表8所示。

表8 漠河地区附面层参数Tab.8 Boundary layer parameters in Mohe district

3 结语

1）由于地域环境差异，不同冻土地区应用附面层理论计算地基温度场时其附面层参数的取值有所差异。

2）根据当地气候气温资料，应用有限元软件建立综合二、三类边界条件的温度场模型，比较不同深度地基温度与附面层理论的拟合度可确定附面层参数。

3）漠河地区跑道多年冻土地基温度场沥青混凝土道面对应的附面层厚度为0.12 m，附面层底地基温度初始值为1.90 ℃，振幅为25.09 ℃；天然地面对应的附面层厚度为0.06 m，附面层底地基温度初始值为1.03 ℃，振幅为25.20 ℃。

4）漠河古莲机场正式通航之后，在多年冻土区建设机场成为可能，根据其附面层参数确定跑道有限元模型，利用有限元模拟分析其未来的温度场变化趋势，为及时发现跑道可能存在的问题提供依据。