图像纹理高强度分布的约束随机编码方法

高庆吉，彭传波，方 榕

（中国民航大学电子信息与自动化学院，天津 300300）

在自助行李托运和自动行李分拣系统中，需要检测行李的规格，包括外观、尺寸、件数、形状等，以便区分超规行李，拒绝托运形状不合规行李。

常用的航空行李三维检测方法有单目图像序列光流法、光电开关和光幕探测法、立体视觉法、激光雷达三维成像法等，其中：单目图像序列光流法对于光照变化、大位移运动等的光流计算结果较差[1]；光电开关和光幕探测法的精度不足，工业级的激光三维成像系统测量复杂大型物体时，测量机位点的布置设计是准确详实获取数据的关键技术[2]，但是对于数据配准仍无合适的解决方案；手持式三维扫描设备生成的模型纹理分辨率不够且部分区域存在高光、阴影及明暗变化的问题[3]。

立体视觉法具有大视场、非接触、信息丰富及高精度等优点[4]，但基于传统的立体视觉法在自然光照条件下对于纯色或纹理特征不明显的航空行李很难进行可靠的立体匹配和三维建模。为了增加被测物体表面的纹理特征，一般采用投影仪在目标表面投影栅格图案的方法来增加立体匹配的精度和可靠性，而投影模型的研究是近年来的一个热点。

徐婵婵等[5]采用邻域直方图匹配的矢量进行纹理合成，有较好的应用意义；Xu 等[6]和Liu 等[7]采用投影激光点阵增强检测目标表面的纹理质量，并得到目标的稀疏点云模型；Yu 等[8]利用在被测物体上投影格雷码的方法进行物体表面的三维重建，其重建精度较高，适用于测量静态物体[9]；刘巍等[10]采用基于彩色编码的空间域编码方法，把所有编码信息集中在一幅图像上，采用一个投影仪和一个摄像机进行被测物体表面的三维重建，可以实时在线检测，由于该编码方法在尽可能少的编码图案中融入更丰富的编码信息，对物体表面的连续性有很高的要求。

基于上述文献的启发，提出了一种随机约束编码的投影图像生成算法。首先，根据立体匹配算法的搜索策略及代价聚合的计算方法，设计了投影图像像素编码规则，形成高强度的纹理分布图像；然后，使用编码后的图像对弱纹理航空行李表面进行主动投影，采用半全局立体匹配算法完成行李表面的三维重建。实验证明，该约束随机编码图像能够显著提高立体匹配的可靠性和三维重建的精度。

1 立体匹配算法

立体匹配通过寻找左右两幅图像中来自同一个空间点投影而成的特征点，构建两特征点的空间关系，从而对场景进行三维重建。半全局立体匹配（SGM，semi-global matching）算法[11]是应用于计算机双目视觉的半全局匹配算法，通过代计算、代价聚合两个关键步骤，在一维方向上搜索左右图像中相同的特征点，并设置了一个全局能量函数，寻找使得能量函数最小化的视差d，以达到求解每个像素最优视差的目的，视差图的能量函数定义为

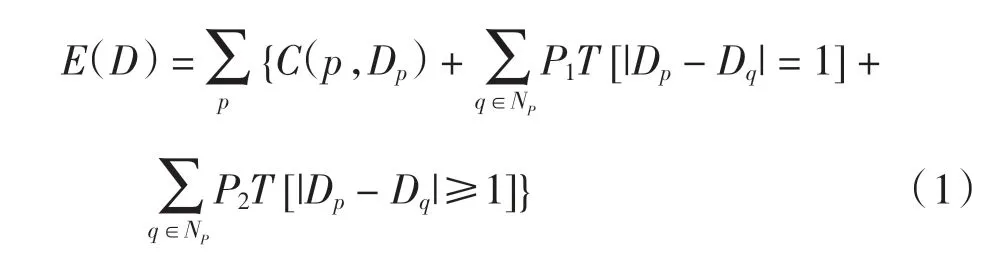
其中，E（D）由3 部分构成：第1 部分C（p，Dp）指该像素的视差为Dp时的匹配代价；第2 部分P1是一个惩罚系数，T[ ]用于对p的邻域与p 像素的视差值为1的像素进行惩罚；第3 部分P2是另一个惩罚系数，T[ ]用于对p的领域与p 像素的视差值大于1的像素进行惩罚。

这样立体匹配问题就可以转换成寻找使得能量函数最小的视差问题，能量函数在二维图像中寻找最优解是一个NP-complete 问题[12]，因此可分解为8

个一维问题，每个一维问题都可以使用动态规划算法求解。

2 约束随机编码模型

2.1 约束条件

从SGM的能量函数计算方法可知，其立体匹配算法从8个一维方向搜索，找到使得能量函数最小的视差值。像素p的能量函数不仅与自身有关，还与其8个邻域像素的能量值有关，因此，设计一种基于8 邻域编码投影模型，使得每个像素及其邻域能量被唯一标识。

在许多情况下，由于物体的遮挡及物体的不连续性使得该像素不可见时，可利用该像素周围的8个像素的能量值来唯一判断出该像素[13]。由于每个像素及其8 邻域内的编码是唯一确定的，所以减小了在立体匹配中找到左右图像相同或相近的特征点的困难。SGM 算法基于移动窗口来寻找左右图像中相同的特征点，这样会使得匹配效率增加。

令P = {p1，p2，…，pn}，p∈（0，255），pn表示每个像素的能量值。这些能量值构成了一个m×n的矩阵M，这个矩阵M 就是约束随机编码模型矩阵。定义一维矩阵，矩阵的位置由下标（i，j）唯一确定，即

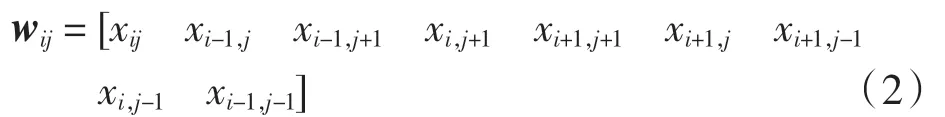
wij由该像素及8个邻域像素组成，8 邻域共分成4个方向（左右、上下和两对角线）如图1所示。

图1 wij 向量元素位置示意图Fig.1 wij vector element position diagram

每个像素与其周围8个像素的能量值都不相同，且根据能量绝对值之差，可设定阈值h，阈值h 越大，该像素与周围像素的能量差值越大，可得约束随机编码矩阵M的构造方式为

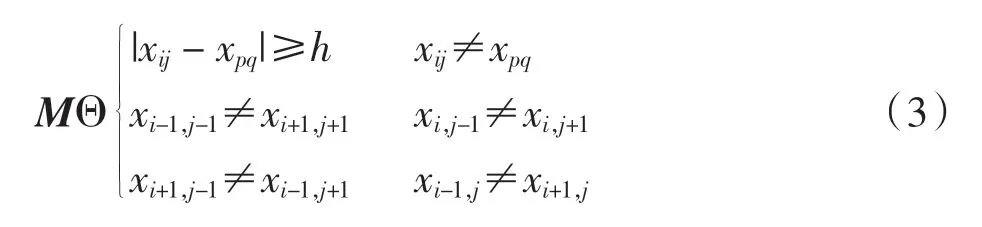
其中，M的约束条件为

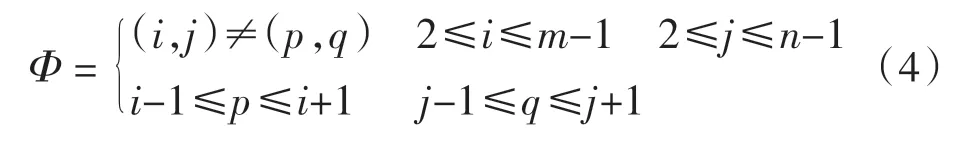
上述约束条件保证了该像素及其8个邻域像素能量值的唯一性，在8个方向上搜索左右两幅图像上同一个像素及其邻域的能量差值最小。

2.2 约束随机编码的生成方法

首先，设置编码模型的高度和宽度，这决定生成约束随机编码投影模型的大小。编码矩阵按照行的顺序依次产生，每次利用随机算法产生一个像素的能量值，之后每个新的像素能量值都会与前面已经存在像素能量值按照编码规则进行能量差值运算，且差值≥h，如果不满足阈值的要求，再次调用随机算法产生新的能量值，重新进行运算，直到产生满足阈值要求的能量值为止。

1）第1 行编码序列

其中：xij表示每个像素能量值的大小，xij∈（0，255）；n表示第1 行像素的个数（与设定的宽度有关），1≤n≤width。第1 行的像素只需与前1个像素进行运算，如图2所示（箭头指向的两个像素作差值运算）。且满足：

图2 第1 行约束随机编码示意图Fig.2 Constrained random coding in Line One

2）第2 行编码序列

第2 行第1个编码单位调用随机算法的生成不需要与任何编码单位进行能量差值运算，第2 行编码序列的第2个单位编码需要与4个编码单位进行差值运算，第3个单位编码需要与5个编码单位进行差值运算，以此类推，最后1个单位编码需要与4个编码单位进行差值运算，如图3所示。

3）第3 行编码序列

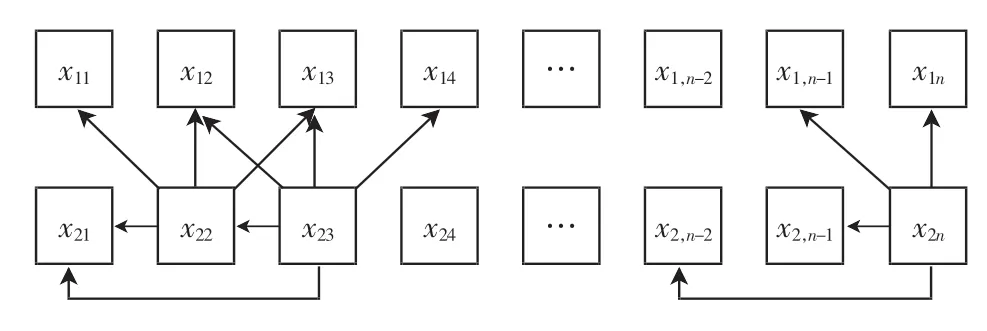
图3 第2 行约束随机编码示意图Fig.3 Constraint random coding in Line Two

第3 行的第1个单位编码需要与2个编码单位进行差值运算；第2个编码单位需要与6个编码单位进行差值运算，如图4（a）所示；第3 行第3个单位编码需要与周围8个编码单位进行差值运算；以此类推第3 行最后1个单位编码需要与6 编码单位进行差值运算，如图4（b）所示。

图4 第3 行约束随机编码示意图Fig.4 Constrained random coding in Line Three

第4 行到最后1 行的编码类似第3 行，当所有行的编码完成之后激光投影编码模型就可以生成了，最终生成约束随机编码模型。

3 实验及结果分析

实验在PC 机上实现，主要配置是：Inter（R）Core（TM）i7-4790 K CPU，4.00 GHz 主频，8.00 G 内存，Window10 操作系统。立体视觉的硬件组成包括笔记本电脑及双目立体视觉相机。双目立体视觉相机由两台Basler dart（daA1280-54uc）工业相机组成，图像分辨率为1 280×960。两台立体视觉相机平行放置，刚性固联，设定基线（可调）为100 mm；相机镜头采用Basler 原装C 口镜头，8 mm 固定焦距，分辨率为500万像素。自助行李托运系统在室内环境下运行，光照比较稳定，左右相机采集的图像光照差异较小，但是相比室外的环境，弱纹理特征会更加突出。

立体视觉实验平台如图5所示，双目相机与水平方向的夹角为30°，约束随机编码的投影装置安装在双目相机的下方，与相机夹角相同，相机安装高度距离自助行李托运系统的传送带上表面1.2 m。

在实验中首先进行了在自然光照条件下的立体匹配实验，如表1所示。由自然光照下生成的视差图可知，对于纯色或弱纹理的航空行李对象，SGM 算法存在极大的误匹配和无法匹配的现象，因此若要得到完整的行李视差图，必须对这种对象进行纹理增强。在表1的对比实验中，采用了立体视觉中常用的纹理增强方法（激光点阵投影，随机数字散斑投影，静态光栅投影）得到行李对象的视差图，并对不同纹理增强方法得到视差图进行分析。

图5 双目立体视觉实验平台Fig.5 Binocular stereo vision experiment platform

表1 不同纹理增强方法对比实验Tab.1 Comparing experiment of different texture enhancement methods

为了验证约束编码模型弱纹理对象立体匹配的鲁棒性，在室内采集了包括自然光照、激光点阵投影、随机数字散斑投影及约束随机编码投影得到的视差图进行匹配的正确率进行统计。图6 是通过立体匹配得到稠密视差图而统计出的无法匹配、正确匹配及误匹配的像素个数分布直方图（像素的灰度值在0～85认为是无法匹配、86～170为正确匹配；171～255为误匹配）。

图6 视差图灰度值分布Fig.6 Gray value distribution of disparity map

从图6 中明显可看出，基于约束随机编码模型正确匹配的概率最高、误匹配率最低，随机数字散斑次之，然后是激光点阵，在自然光照条件下正确匹配的概率最低。

纹理质量是立体视觉状态检测研究的核心技术，在工业生产领域起着重要的作用[14]，较高的纹理质量可以大幅提高立体匹配的质量。

积分灰度方差是能够反映图像纹理质量的评价依据[15]，一个窗口内的灰度值方差可表示为

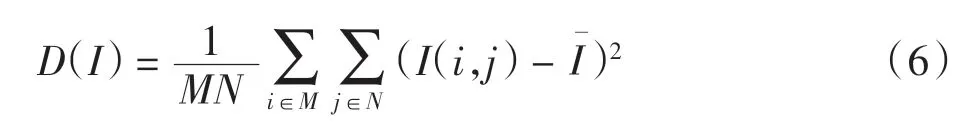
通过平面测量的方法对比实验分析约束随机编码模型下航空行李三维重建的精度。在实验中选择不同颜色和不同形状的航空行李进行多次测量取平均值作为航空行李的真实测量值，以三维重建之后的点云到拟合平面距离最大值作为三维重建的精度值进行误差计算[16]，结果如表2所示。

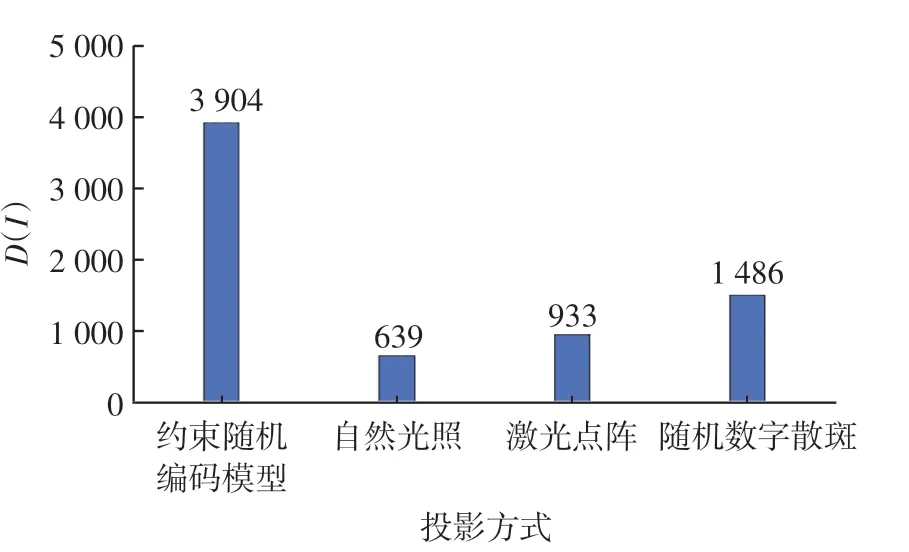
图7 积分灰度方差Fig.7 Integrated gray scale variance

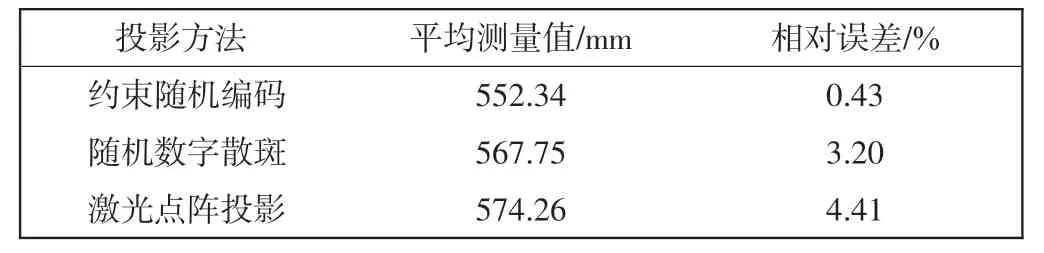
表2 行李箱三维重建测量精度Tab.2 3D reconstruction measurement accuracy of baggage

从表2 中可知，约束随机编码投影误差比为0.43%，远低于随机数字散斑投影方式和激光点阵投影方式，可显著提高弱纹理行李对象立体匹配的可靠性和三维重建精度。

4 结语

为了解决弱纹理行李对象的三维建模困难问题，研究了一种随机约束编码的投影图像生成算法。设计了投影图像像素编码规则，建立了投影与目标混合图像位置像素局部唯一性约束下的计算方法，形成高强度的纹理分布图像；使用编码后的图像对弱纹理航空行李进行了主动投影，采用半全局立体匹配算法完成行李表面的三维重建。由实验结果可知，该约束随机编码模型可显著增强双目立体视觉系统中立体匹配可靠性和三维重建的精度，可用于行李适运性检测。