预制拼装钢管混凝土自复位桥墩变形分析模型及验证
李 宁,张双城,李忠献,谢礼立,3
(1. 天津大学建筑工程学院/滨海土木工程结构与安全教育部重点实验室(天津大学),天津 300350;2. 中国地震局地震工程综合模拟与城乡抗震韧性重点实验室(天津大学),天津 300350;3. 中国地震局工程力学研究所,哈尔滨 150080)
目前,桥梁抗震设计采取基于延性和考虑能力保护构件的抗震设计方法,主要通过塑性铰区材料的塑性变形耗散地震能量。虽然能够有效地防止桥梁结构倒塌,但在强震作用后,墩柱塑性铰区往往损伤严重,且墩体残余位移较大。近年来,一方面,自复位结构成为实现损伤可控、满足震后使用功能和达到特定可恢复性能的一种选择[1]。另一方面,桥梁建设也在不断创新发展新的施工方法以提高桥梁结构的建设速度和质量,减少全寿命周期成本及其对环境的不利影响。节段预制拼装技术成为替代现浇施工的最有竞争力的建造方法之一[2]。结合节段拼装技术和损伤可控设计思想,节段拼装自复位桥墩应运而生[3],然而其设计理论和分析方法仍存在许多问题待解决。
为了使节段拼装自复位桥墩在地震作用下具有足够的自复位能力和抗剪能力,需要施加适当的预应力。而动力作用中节段间接缝的张开和闭合使得节段局部受压损伤,产生预应力损失,导致节段间较容易发生剪切滑移甚至破坏[4]。为此,Hewes和Priestley[5]在底部塑性铰区采用钢管混凝土节段,利用钢管约束效应减小墩底接缝处混凝土损伤。对桥墩多处出现塑性铰的行为,为了避免第二个接缝处产生明显损伤,张强[6]进行了所有节段均采用CFST的节段拼装自复位桥墩拟静力试验。
由于节段拼装自复位桥墩允许底节段和承台间摇摆,虽然避免了在墩底形成塑性铰,而耗能能力可能不足。为了提高节段拼装自复位桥墩的耗能能力,Ou等[7]通过设置通长的耗能钢筋以提高节段拼装自复位桥墩的抗震能力,并给出节段拼装空心混凝土自复位桥墩耗能钢筋的合理用量。Marriott等[8]提出在桥墩底部设置外包钢管的耗能钢棒,并通过拟静力试验验证了耗能钢棒在耗能能力方面的优越性。
在理论分析模型方面,Pampanin等[9]将预制拼装桥墩和现浇桥墩对比,提出了“等效悬臂梁理论”(MBA),补充了除力的平衡条件外的变形协调条件。Palermo等[10]在Pampanin等[9]的基础上,考虑了现浇桥墩形成塑性铰前预制拼装桥墩底接缝已经张开,提出修正的“等效悬臂梁理论”,更好地预测预制拼装桥墩的变形行为。郭佳等[11]基于Euler梁理论提出了自复位桥墩的荷载-位移简化分析模型。Bu等[12-13]基于截面弯矩-曲率分析,提出了单节点推覆分析方法和多节点转动推覆分析方法。上述解析分析方法虽然与试验吻合良好,但均需要迭代。
为了避免迭代,Wang等[14]建立了节段拼装矩形空心自复位混凝土桥墩推覆曲线的显式分析模型,该方法将预制拼装桥墩底接缝张开对侧移的贡献等效为塑性铰转动对侧移的贡献,截面张角等于塑性转角,实际上耗能钢筋屈服前截面已经张开,因而求得的底节段张角将会偏小。另外,截面形式的不同也会影响截面的应力分布模式,变形状态的判定规律也不同。
本文在理论分析模型的基础上,针对节段拼装自复位桥墩和现浇桥墩的变形特点,考虑了耗能钢筋无粘结段和混凝土应变渗透引起的粘结滑移,采用“图乘法”和“修正的等效悬臂梁理论”,建立了适用于内置耗能钢筋的节段拼装圆形CFST自复位桥墩变形分析模型,并与拟静力试验结果和基于纤维截面的模拟模型对比,验证所提出模型的正确性。
1 节段拼装CFST自复位桥墩分析方法
1.1 节段拼装CFST自复位桥墩力学特性
内置耗能钢筋的节段拼装CFST自复位桥墩是由CFST节段、无粘结预应力钢筋、局部无粘结耗能钢筋组成,将预应力技术和摇摆行为相结合,具有自复位、低损伤的特点[15]。耗能钢筋的无粘结段采用基于屈服诱导机制的变径处理,无粘结段率先屈服,在波纹钢套管内浆料的约束下如同一个内置的BRB耗能器,更好地发挥耗能钢筋的耗能能力。
构件中的预应力钢筋一方面作为弹性元件可以提高桥墩的屈服后刚度比、减小残余位移、利于震后快速修复[16],另一方面,通过预应力张拉可使节段间、节段和承台间产生压紧力进而增加摩擦力,保证节段拼装桥墩的整体性和接缝处具备可靠的抗剪能力。耗能钢筋作为弹塑性元件在提供抗侧刚度和承载力的同时,利用接缝张开闭合时的拉压屈服来耗散能量。更重要的是无粘结段的设置有效避免了应力集中,推迟了耗能钢筋过早发生低周疲劳破坏,有效地发挥了钢筋延性耗能能力[7]。预应力钢筋提供的自复位特性和耗能钢筋提供的耗能能力使得节段拼装自复位桥墩表现出“旗帜型”的滞回曲线,虽然耗能能力略显不足,但也表现出令人满意的抗震性能[17]。
与传统桥墩依赖材料的非线性行为特性、提供足够的变形延性机理不同,节段拼装CFST自复位桥墩放松了桥墩与承台的约束,通过接缝张开和闭合实现刚度自适应转变,延长自振周期,从而避开地震能量相对集中的频段,具有摇摆隔震的相似功能[11]。
1.2 节段拼装CFST自复位桥墩的变形分析模型
对于节段拼装CFST自复位桥墩,本文定义了三种特征状态:消压极限状态、等效屈服极限状态和可恢复设计极限状态,分别计算其在不同状态下的力学行为,得到变形分析模型,为设计理论提供支撑。
1.2.1 消压极限状态
当水平荷载在墩底截面形成的弯矩产生的拉应力恰好抵消重力和预应力产生的压应力时,称为消压极限状态。此时,截面即将张开,墩顶的位移全部由桥墩的弯曲变形提供,侧移行为可按墩底刚接的现浇桥墩进行计算。针对桥墩的受力和变形特点,给出消压极限状态变形分析模型的应力和应变解答。
应变解答:由于钢管和混凝土刚度差异较大,相同荷载作用下两者的应力分布不均匀,但钢管和混凝土之间有良好的粘结力,两者应变协调,可以确定载荷、变形。
在消压极限状态(图1),全截面受压,平截面假定依然成立,钢管混凝土的应变为:


图1 消压极限状态底接缝的应变分布Fig.1 Strain distribution of the bottom joint at decompression limit status
相应的墩底截面的曲率、弯矩为:

进一步得到墩顶位移和基底剪力:

式中:PG和PPT分别表示上部结构的总重力和初始预应力;Ea、Ia、ρEB分别为耗能钢筋的弹性模量、截面惯性矩和配筋率;Ec、Ic、Ac分别为混凝土的弹性模量、截面惯性矩和面积;Es、Is、As分别为钢管的弹性模量、截面惯性矩和面积;Isc和D分别表示配筋钢管混凝土的抗弯刚度和截面直径;L表示桥墩的剪跨。
应力解答:针对消压状态时钢管和混凝土应力分布的特点,建立求解受压区钢管和混凝土合力及合力矩的图乘法,进行消压状态下CFST自复位桥墩的变形行为的解析分析。
在消压状态时,底截面受压区边缘的最大压应力很小,假定钢管和混凝土各自的压应力呈线性分布[18]。
如图2所示,为了不失一般性,假定受压区为任意形状,受压区能够提供的合力和力矩分别为:当受压区应力呈线性分布时可进一步简化为:


式中:A和xc分别代表受压区的面积和形心坐标;和分别代表截面形心处的应变和应力;iy表示任意截面对y轴的惯性半径;和分别代表处(见图2)的应变和应力。

图2 图乘计算时任意截面的应力分布Fig.2 Stress distribution of arbitrary section using graph integral calculation
此时,受压区对坐标原点的力臂为:

当受压区为钢管混凝土圆形截面时,受压区钢管或混凝土可以提供的合压力和对圆心的力臂分别为:

式中:R和r分别为钢管混凝土的外径和内径;Mc、、iyc、xc和Ms、、iys、xs分别为受压区混凝土和钢管提供的弯矩、平均应力、惯性半径和截面形心。
此时,受压耗能钢筋的合压力分别为:

式中:d′为受拉或受压耗能钢筋到就近截面边缘的距离;AED,l和AED,r分别表示圆心左侧和右侧的耗能钢筋面积。
以底截面为研究对象,对重力和预应力的合力点取矩,得到底截面的弯矩:

当水平力产生的倾覆弯矩超过 Md时,底截面就会张开,故Md也称为临界张开弯矩。
基底剪力和墩顶水平位移的计算见方法1。
综上,消压极限状态时桥墩变形分析模型的应变和应力解答可求出,两者结果对比详见第3节。
1.2.2 等效屈服极限状态
圆形截面的特殊性使得当耗能钢筋沿圆周布置时,为逐渐屈服的过程。为了方便设计,借用“等效屈服点”的概念定义了适合圆形截面节段拼装CFST自复位桥墩的等效屈服极限状态。由于接缝的张开,实际的截面变形不再满足平截面假定。
根据“修正的等效悬臂梁理论”[10],得到节段拼装CFST自复位桥墩在等效屈服状态时的底截面张角:

式中:φd为截面的消压曲率,由式(2)算出;φy为屈服曲率[19],可以表示为:

式中,εy为耗能钢筋的屈服应变。
当耗能钢筋屈服时,以底接缝为研究对象进行受力分析,如图3所示,受拉侧屈服的耗能钢筋提供的合拉力为:

此时,预应力钢筋的应变增量为:

预应力筋的应力增量为:

预应力筋的拉力增量为:

受压区耗能钢筋提供的合压力为:
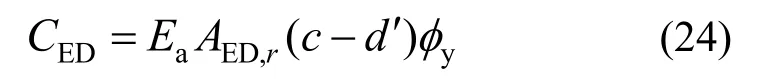
式中:lPT和ΔPT分别表示预应力筋的初始长度和伸长量;c和 D分别为受压区高度和截面直径;EPT和APT分别代表预应力筋的弹性模量和面积。
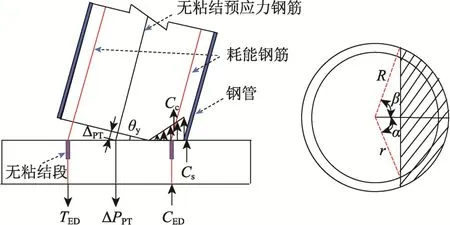
图3 屈服极限状态时底接缝的示意图Fig.3 Schematic diagram of the bottom joint at the yield status
对于核心混凝土,采用韩林海[20]提出的约束混凝土本构。屈服极限状态底截面的张角仍很小,受压区边缘混凝土的最大应力远远小于峰值应力,因此,受压区约束混凝土的应力-应变关系可以简化为[12]:

式中:0σ和0ε分别为峰值应力和峰值应变;Eceq为等效弹性模量。
利用图乘法求解受压区混凝土和钢管提供的合压力:

式中,α和β的几何参数说明见图3。根据底截面轴向力的平衡方程:

进而得到一个关于受压区高度c的一元三次方程:

当受压区高度c已知,预应力钢筋的拉力增量、受压区耗能钢筋的压力以及受压区混凝土和钢管的合压力可分别按式(23)、式(24)、式(26)、式(27)计算出来。
此时,底截面的弯矩就可以表示为:
其中:

式中,MyED、 Myc、Mys分别表示耗能钢筋、受压区混凝土和钢管对截面中心的抵抗弯矩。
耗能钢筋屈服时,基底剪力为:

节段拼装摇摆自复位桥墩的墩顶位移主要由节段转动、桥墩弯曲变形、剪切变形以及节段间的滑移变形四部分组成,由于节段间的摩擦力足够抗剪,节段间的滑移很小。因此,只考虑弯曲变形、剪切变形和刚体转动对墩顶水平位移的贡献[21]。这样,墩顶位移表示为:

式中:Kθ和 Kv分别表示桥墩的抗侧刚度和抗剪刚度;EIeff表示钢管混凝土的等效抗弯刚度,假定节段张开前取EIsc,张开后取0.7EIsc[21],屈服状态底节段已经张开故等效抗弯刚度取0.7EIsc。
1.2.3 可恢复设计极限状态
对于钢管混凝土摇摆自复位桥墩,由于钢管对核心混凝土提供有效的约束,混凝土的损伤较小,而预应力钢筋在节段拼装摇摆自复位桥墩中提供连接和自复位的功能,在设计时应该避免预应力钢筋的屈服。为了确保桥墩具有良好的震后快速恢复能力,我们偏于保守地把耗能钢筋无粘结段断裂、钢管不失效、受压区混凝土不受压破坏作为可恢复设计极限状态。在地震作用后桥墩的承重体系和自复位体系无须修复,可以确保其在非地震工况下的正常使用。此外,即使内置的耗能钢筋震后无法更换,还可以补设外置耗能器满足地震工况下的耗能需求。
耗能钢筋无粘结段优先屈服、断裂由式(42)保证,受压区混凝土不发生受压破坏和钢管不失效通过式(43)和式(44)保证:

具体地:

式中:d1和fu1分别为耗能钢筋无粘结段的直径和极限抗拉强度;d2和fy2分别为无粘结段两端的钢筋直径和屈服强度;εmax和εcu分别为受压区混凝土的最大压应变和极限压应变;σ1和σ2分别为钢管轴向压应力和环向压应力;[σ]为钢管在单向受力状态下的极限强度;ρj为约束钢的体积比;εsu为最大应力时钢材的应变;fcc为约束混凝土的强度;t为钢管的厚度;L和LP分别为桥墩的高度和塑性铰长度;fy为耗能钢筋的屈服强度;σc为核心混凝土的最大压应力;dc为核心混凝土的直径;p为约束压力。
为建立桥墩在可恢复设计极限状态下的变形分析模型,做以下假定:
1) 受压区混凝土的压应力采用等效矩形应力表示,等效应力系数按文献[11]选取;
2) 钢管局部受压,均达到屈服强度fy;
3) 耗能钢筋采用三折线数学模型[22],屈服后刚度比参考钢筋的材性实验结果进行确定。
考虑耗能钢筋的无粘结段两端和混凝土应变渗透引起的粘结滑移,当底节段产生张角θgap时,受拉耗能钢筋的应变为[10,12]:

式中:Lub为耗能钢筋预留的无粘结段长度;ΔED,l为截面张开引起耗能钢筋的伸长量,可以表示为:

式中,ΔED,pl为应变渗透引起耗能钢筋的伸长量,可以表示为[15]:
应变渗透引起的等效无粘结长度为[13]:

式中,fg为灌浆料的抗压强度;db为耗能钢筋的直径。
Ou等[7]发现接缝张开过程对Leu并不敏感,为了方便计算可取:

受拉耗能钢筋的应力为:

这样,耗能钢筋提供的拉力为:

预应力筋的拉力增量为:

采用“修正的等效悬臂梁理论”[10],得到底截面受压区的曲率:

式中,LP为等效塑性铰长度,可以表示为[23]:

可恢复设计极限状态受压耗能钢筋、混凝土、钢管提供的压力分别为:

由可恢复设计极限状态下轴向力的平衡方程(同式(32)),得到关于受压区高度 c的一元一次方程,从而通过式(57)、式(58)、式(61)~式(63)获得任意张角θgap时受拉区耗能钢筋的拉力、预应力钢筋的拉力、受压区耗能钢筋的压力以及受压区混凝土和钢管的合压力。
可恢复设计极限状态下的墩顶水平位移和基底弯矩同等效屈服极限状态。
1.2.4 适用条件
已有研究结果表明[7],对于以弯曲破坏的预制节段拼装自复位桥墩,墩顶位移主要由底接缝张开引起。故上述变形分析模型推导没有考虑其他接缝张开对侧移的贡献,但有必要给出适用该分析模型的桥墩底节段高度的下限值。
方法 1:由第二个接缝处重力和预应力产生的压应力不被弯矩产生的拉应力抵消确定底节段高度:

式中:Fpk和Δpk分别为峰值承载力和峰值位移;A和W分别为截面的面积和抗弯截面模量;L1表示底节段的高度。
方法 2:由第二个接缝的峰值弯矩不超过消压弯矩确定底节段高度:

式中,Mpk和Md分别表示底接缝的峰值弯矩和消压弯矩。严格满足该变形分析模型的底节段高度可由式(64)或式(65)确定。
综上,论述了预制拼装CFST自复位桥墩变形分析模型的解析分析过程。为了方便设计,给出如图4所示的流程图。

图4 变形分析模型流程图Fig.4 Flow chart of deformation analysis model
2 变形分析模型的初步验证
由于预制节段拼装圆形CFST自复位桥墩的拟静力试验较少,为验证提出的变形分析模型,采用郭佳等[11]的自复位桥梁墩柱拟静力试验,进行对比分析。此时,上述计算式不考虑外置钢管的贡献,对应的混凝土本构采用Kent-Park模型[24],计算结果见图5。
通过对比发现,Wang等[14]采用塑性转角代替截面张角的变形分析模型,在屈服极限状态前刚度偏大,本文提出的模型和试验相差较小。与郭佳等[11]提出的基于 Euler梁理论的迭代分析模型相比,本文提出的变形分析模型不需要迭代和截面积分,计算更方便,设计极限承载力基本一致,但屈服前刚度和试验吻合更好。另外,消压极限状态的应变解答和应力解答吻合较好。也证明了本文方法对非钢管节段自复位构件变形分析的通用性。

图5 提出的模型与试验和相关分析模型的对比Fig.5 Comparison of the proposed model with the experimental results and previous analysis models
3 变形能力分析模型的进一步验证
为了进一步验证提出的分析模型,采用纤维截面的模拟模型和 CFST墩的拟静力试验进行对比验证。
3.1 基于OpenSees平台的纤维模型
采用OpenSees平台建立如图6所示的节段拼装钢管混凝土自复位桥墩的纤维模型。其中,钢管混凝土节段采用DispBeamColumn单元,混凝土本构采用Concrete01材料,不考虑混凝土抗拉强度;钢管本构选用 Steel02单轴材料本构,可反映钢材的 Bauschinger效应和等向强化效应。无粘结预应力筋采用CorotTruss单元,分离建模,顶部和桥墩共节点,底部固定,本构关系采用Elastic-PP单轴材料,通过设置初应变的方式施加预应力。此外,采用 ZeroLength单元和ZeroLengthSection单元并配以Elastic-No Tension材料模拟接缝,利用单压材料的不抗拉特性模拟底节段和承台以及上部节段间的分离和转动。耗能钢筋采用Truss单元进行模拟,采用 Steel02单轴材料本构,为了使耗能钢筋与桥墩变形协调,在同一高度处采用RigidLinkBeam单元与梁柱单元连接。

图6 节段拼装自复位桥墩的纤维模型Fig.6 Fiber model of precast segmental self-centering bridge
3.2 拟静力实验概况
试验CFST自复位桥墩由三个节段、加载端和承台组成。墩高 1.8 m,加载点到承台顶面的有效高度为2 m。圆钢管截面外径400 mm、壁厚6 mm,Q235钢材,内填C40混凝土。截面中心贯穿无粘结预应力筋 6×7Φs15.2,极限抗拉强度标准值为1860 MPa,张拉设计值为300 kN。上部结构设计重力为500 kN,为了加载方便,以预应力形式施加重力,总的预应力张拉设计值为 800 kN(轴压比为0.166)。耗能钢筋选用 HRB400级钢筋,距截面边缘40 mm,在150 mm的无粘结段处变径,两端采用机械套筒连接。具体设计细节见图7。

图7 具体设计细节Fig.7 Specific design details
本试验在天津大学滨海土木工程结构与安全教育部重点实验室进行,如图8所示,采用500 kN的电液伺服作动器进行拟静力加载。整个加载过程采用位移控制,按位移角0.5%的整数倍进行单周往复加载,水平向最大位移角达到5%时终止试验。
3.3 模拟模型、实验结果和本文方法的验证
CFST自复位桥墩的变形分析模型与纤维截面模拟模型、试验结果数据对比如图9所示。可见骨架曲线吻合良好,说明本文方法对关键状态点有较好的估计精度;此外,对比了结构设计所关心的消压状态、等效屈服状态和可恢复设计极限状态下的抗弯承载力,与实测值的误差分别为7.02%、6.38%和11.06%,如表1所示。表明本文提出的模型的有效性。

图8 试验加载图Fig.8 Test loading diagram

图9 提出的模型与试验和模拟的对比Fig.9 Comparison of proposed model with experiment and simulation

表1 抗弯极限承载力对比Table 1 Comparison of ultimate bending capacity
4 结论
本文提出的变形分析模型将桥墩的变形行为分为3个阶段:消压极限状态、等效屈服极限状态和可恢复设计极限状态。消压极限状态底接缝不张开,按墩底刚接的现浇桥墩计算承载力和墩顶位移;对等效屈服极限状态和可恢复设计极限状态通过计算受压区高度进而计算承载力和墩顶位移,得到以下结论:
(1) 本文提出的变形分析模型考虑了桥墩的弯曲变形、剪切变形和接缝转动的贡献。与传统的迭代方法相比,该分析模型不需要迭代,采用“图乘法”计算,力学过程更明晰,计算更便捷,且精度较高。
(2) 该分析模型考虑了耗能钢筋的无粘结段和混凝土粘结滑移引起的应变渗透效应,通过“修正的等效悬臂梁理论”确定截面张角和受压区曲率,与拟静力试验得到的消压承载力、等效屈服承载力和可恢复设计极限承载力分别相差 7.02%、6.38%和11.06%,较好地预测预制拼装CFST自复位桥墩的荷载-位移关系曲线,为同类型结构构件的结构设计、分析提供参考和理论支撑。

