组合材料加固砖砌体的有限元模拟方法
陈再现,杨续波
(哈尔滨工业大学(威海)土木工程系,威海 264209)
砌体结构以其成本低、材源广、耐久性和耐火性好、施工方便等优点,在我国工业与民用建筑领域得到广泛应用。但砌体结构自重大、抗剪性能差,导致其在地震中损坏严重[1]。加固是目前提高既有砌体结构性能的主要手段,国内外学者对其进行了大量试验研究,部分学者对砌体有限元编程作了有益尝试。
戴如之[2]利用ANSYS建立分离式砌体模型对水平嵌筋加固砌体墙的开裂性能进行研究;朱成成等[3]利用ABAQUS建立水平嵌筋加固砌体模型,通过弹塑性动力分析研究嵌筋间距对加固效果的影响。上述有限元模型均基于理论分析阐述其可行性,缺乏试验数据,有待进一步研究。另有学者基于试验数据,建立砌体有限元验证模型,来评估加固砌体抗震性能。黄斌和阿肯江·托呼提 提出等效体积单元(RVE)法,利用ANSYS建立整体式砌体模型,对钢丝网水泥砂浆加固方法进行研究;Garofano等[5]利用 DIANA软件建立聚合物面层加固砌体有限元模型,并就砌体强度、墙体形状、砂浆强度等因素进行变参数分析;杜德润等[6]运用ABAQUS建立型钢加固砌体墙模型,研究钢材最佳布置方案;Lignola等[7]通过DIANA软件建立二维有限元模型以模拟分析纤维增强水泥基质加固砌体(FRCM)对角压缩试验。此类有限元模型是将验证后的未加固砌体模型直接用于加固砌体变参数分析,加固砌体缺少试验数据,有待深入研究。还有一些学者基于大量试验,分别建立了未加固砌体和加固砌体有限元验证模型,对砌体加固性能进行系统研究。张斯等[8]利用ABAQUS零厚度Cohesive单元考虑砌筑形式建立纤维布加固砌体分离式模型,进行低周往复加载下性能的研究;Susila等[9]考虑砂浆界面滑移效应,采用ABAQUS建模研究竹竿穿孔加固砌体性能、破坏形态及承载力拟合良好;王亭等[10]基于RVE法,运用ANSYS建立砌体整体式模型来研究钢筋网水泥砂浆抹面加固砌体试件的抗震性能。褚少辉等[11]运用ABAQUS研究应力比、高宽比、纤维布层数等因素对碳纤维布加固砌体性能的影响;Dolatshahi等[12]采用ABAQUS/Explicit模块来研究墙体变形能力的主要影响因素,破坏形态模拟良好;陈莹等[13]基于玻璃纤维复合材料加固砌体,提出了考虑粘结剥离效应的数值建模方法,并从块体层面验证了其可行性。Ombres和Verre[14]运用ABAQUS建立宏观模型对水泥基质(FRCM)约束砌体柱进行结构性能分析。
上述有限元模型建模方法尚存在如下不足:一方面,模型仅含有单一加固材料,对于组合材料加固模型的建模研究相对较少,通常忽略加固材料失效以及同砌体间的滑移剥离效应;另一方面,加固模型普遍缺乏必要的试验组验证,验证指标偏少,缺乏普适性,用于加固砌体变参数分析需作进一步优化。为此,本文依托内置钢板聚合物砂浆面层砌体加固法[15]相关试验,基于ABAQUS有限元软件建立加固砌体模型,探讨建模方法和计算效果。
1 砌体数值模拟原理与建模方法
对于砌体数值分析方法的研究,在于寻求最佳建模方法,实现在节约计算资源和时耗的同时提高分析精度,主要包括基本假定选取、建模方法选取、本构关系的选取三个部分。
1.1 建模思路与基本假定
砌体结构的基本组分是砖块体和砂浆,因此砌体有限元模型的建模方法一般分为分离式和整体式两大类。本文综合考虑计算精度和计算效率因素,以未加固砌体整体式模型为基础,结合分离式思想建立加固砌体有限元模型。
对于加固砌体的建模,通常思路是选用实体部件建立砌体墙片;线性部件或壳体部件模拟加固钢材和加固面层。但此类建模方法,所用单元类型多,维度不一,单元连接处理不理想;且线形部件无法模拟钢板屈曲与焊口断裂现象。基于上述原因,文中砌体及各类加固材料均选用实体部件建立。
模型建立所用到的基本假定包括连续性假定、匀质性假定与各向同性假定。其中,连续性假定要求宏观构件尺寸比块体大五倍以上[16],砌体、钢板及聚合砂浆面层均符合条件。其次,砌体虽然由块体、砂浆组成,但考虑到各组分空间排布均匀,这里假设其同加固钢板、砂浆一样为单一材质,即满足匀质性假定。此外,鉴于砌体弹性模量在水平、垂直方向上的差异较小,泊松比影响不大,因此在宏观分析中可将其视作各向同性匀质体。对于钢板、聚合物砂浆而言,它们的物理力学特性在各方向亦无显著差异,基本满足各向同性假定。
1.2 单元选取与建模方法
所涉及的单元类型包括实体单元、接触单元和生死单元三类。其中各类材料部件的主体部分均采用八节点六面体线性减缩积分实体单元(C3D8R),砂浆面层与砌体连接部分采用零厚度的Surface Cohesive接触单元;加固钢板焊缝引入生死单元进行模拟。
C3D8R单元优点是位移求解精确、单元扭曲稳定性好、适于接触分析、不易发生“剪切自锁”[17]。对于C3D8R单元不适于模拟应力集中及产生“沙漏”数值问题,ABAQUS引入“沙漏刚度”来限制沙漏的扩展,模型中的单元越多限制作用越有效[17]。因此,文中通过细化网格来解决“沙漏”问题。Surface Cohesive单元的特点是能够同时满足相对位移和应力传递要求,单元厚度为零,适于模拟粘结滑移。钢板焊缝处生死单元通过对 C3D8R单元材性赋予断裂判据来完成单元的移除,即“杀死”失效单元。
未加固砌体模型由砌体墙片、加载顶梁及底梁三部分组成,通过Tie命令绑定连接,加载底梁底面设置为完全固定约束,竖向荷载以压强形式施加于加载顶梁顶面;为确保加载梁在侧向加载过程中保持水平,在加载顶梁顶面施加竖向位移限制;在加载梁左侧面心处设置参考点 FXB作为侧向位移加载点,并通过位移 Amp表控制施加与真实试验相同的位移加载历程,最后由Coupling命令将二者建立运动(六自由度)耦合关系。
加固砌体模型建立在未加固砌体模型基础之上。具体建模步骤如下:
1) 创建部件。分别创建聚合物砂浆面层及各类加固钢板部件,之后将加固扁钢、包角角钢及连接角钢依照试验墙体构造完成墙面布置,采用Merge命令合并形成加固钢骨架部件。
2) 划分单元。将各部件划分成规则几何集合体,然后采用结构化网格技术划分单元,见图 1,其中单元划分尺度控制系数设置为0.2。

图1 各材料部件单元划分Fig.1 Breakdown of material components
3) 赋予材性。输入各类材料的材性数据,生成各自的材料截面属性,然后将材料截面属性分别赋予到相应的材料部件实体上。
4) 装配部件。通过平移、旋转等操作,将加固钢骨架部件紧贴砌体墙面布置,然后将聚合物砂浆面层部件包裹在砌体墙部件和加固钢骨架部件外围,装配形成如图2所示的加固砌体。
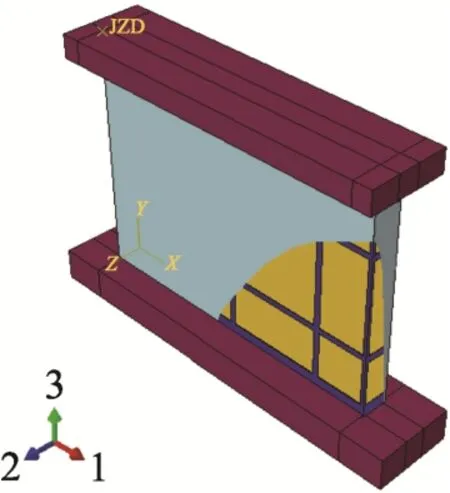
图2 加固砌体模型装配Fig.2 Assembly of reinforced masonry model
5) 创建分析步。在Initial分析步后增设VVV、HHH、FXB三个分析步。分别用于施加竖向荷载,控制加载顶梁水平度和墙体U1方向的侧向位移加载;三者依次生效,并继承至后续分析步。
6) 创建相互作用。首先通过Tie命令将包角角钢四端分别与顶、底梁相连。然后经面-面Tie命令完成加固钢骨架与聚合物砂浆面层的连接。最后由点-面接触将聚合物砂浆面层与砌体建立连接。
7) 处理边界条件。考虑到对拉螺栓及试验墙体侧向支撑的作用,通过对加固钢板对拉螺栓连接处设置边界条件来限制平面外位移,见图3。

图3 加固砌体边界条件设置Fig.3 Conditions for reinforcement of masonry boundary
8) 提交分析。模型数值计算由ABAQUS软件Standard静力分析模块完成。分析流程详见图 4,本文砌体有限元模型的计算终点取荷载下降至极限荷载85%[18]以下的时刻。

图4 模型数值分析流程图Fig.4 Flow chart for numerical analysis of model
1.3 材料本构与破坏准则
砌体和聚合物砂浆面层为基于混凝土塑性损伤模型(CDP)建立,包含屈服函数、流动准则和本构关系三部分。其中前两部分需要指定屈服函数和D-P流动准则中偏平面上的剪胀角ψ、偏心率e、双轴受压强度与单轴受压强度比σb0/σc0、拉压子午线上第二应力不变量的比值K和材料粘滞系数μ等。粘滞系数主要影响计算收敛性与计算精度,取值不宜过大。上述各参数取值参见表1。

表1 屈服函数及流动准则相关参数Table 1 Correlation parameters of yield function and flow criterion
CDP模型的本构关系设置包括各向同性弹性和各向同性损伤塑性两部分,弹性部分需指定弹性模量与泊松比;损伤塑性部分需指定材料的本构关系及损伤演化规律。
砌体受压本构关系采用杨卫忠模型[19]:

式中:σ、fm分别为砌体受压应力值、抗压强度平均值;ε、εm分别为砌体受压应变值、峰值应变值;η为砌体弹性模量与峰值变形模量之比,取1.633。
砌体加卸荷过程损伤演化表达式[19]为:

式中:d为砌体受压(受拉)损伤因子;E0为砌体弹性模量。
聚合物砂浆受压本构关系选用朱伯龙模型[20]:

聚合物砂浆加卸荷过程损伤演化表达式[21]为:

鉴于砌体和砂浆面层的抗拉强度均远低于各自抗压强度,为简化分析,可将受拉本构曲线上升段视作直线,即受拉弹性模量取值同受压弹性模量;受拉本构曲线下降段采用规范[22]附录C.2中给出的混凝土受拉本构关系曲线。
钢筋本构采用强化双折线模型,强化段变形模量取弹性模量的0.001;对于各类加固钢材连接处的角焊缝,据文献[23]附表1.3中Q235钢角焊缝与对接焊缝之比,取强度折减系数为0.744;角焊缝材料属性考虑金属柔性损伤,断裂应变设置为 0.033,损伤演化简化为直线,破坏位移假定为0.5 mm。
加固砌体模型中聚合物砂浆面层与砌体间的接触单元考虑界面粘结属性。界面粘结属性包括切向行为和法向行为。其中切向行为采用库伦模型;摩擦系数据规范[24]取钢材、混凝土沿砌体滑动的平均值 μ=0.575;法向通过添加粘性行为来模拟聚合物砂浆面层同砌体间的粘结滑移效应。粘结界面的接触力损伤演化规律参见图5。

图5 粘性行为损伤演化示意图Fig.5 Evolution of viscous behavior injury
ABAQUS接触属性中的粘结属性需要指定弹性刚度矩阵。本文不考虑刚度耦合效应,只需指定三个主应力方向的刚度knn、kss及ktt。关于粘结界面三向刚度的取值,可由式(7)、式(8)[25]确定:

式中:knn、kss、ktt分别为粘结界面法向、第一切向、第二切向刚度;hm为聚合物砂浆面层厚度;Em、Gm分别为聚合物砂浆弹性模量、剪切模量;Eb、Gb分别为砌体弹性模量、剪切模量。
考虑到聚合物砂浆良好的粘结性能及界面剂的使用,认为加固面层损伤起始取决于砌体轴心抗拉、抗剪强度平均值,具体计算公式[24]分别为:

式中:ft,m为砌体轴心抗拉强度平均值;fv0,m为砌体抗剪强度平均值;f2为砌筑砂浆抗压强度平均值。
采用二次应力准则[26]作为粘结力损伤起始判据,即满足式(11)条件后时损伤开始。演化规律采用能量定律,其中I型断裂能G11与II型断裂能G12、G21依照砌体轴心抗拉、抗剪强度等比换算[27]得到,指定能量定律指数为3,粘滞系数取0.0001。

式中:〈tn〉、〈ts〉、〈tt〉分别为粘结界面法向、第一切向、第二切向接触应力;分别为粘结界面法向、第一切向、第二切向最大应力。
2 砌体数值模型验证与结果分析
2.1 试验模型简介
选取文献[15]中两类共计八面加固墙体为分析对象,图6为试验加载装置,试验墙体尺寸及构造情况见图7,墙体编号及材性信息见表2。墙体高宽比为0.71,厚度为240 mm。各加固墙的竖向荷载均为600 kN。加固钢材强度等级为Q235级,材性试验结果如表3所示。聚合物砂浆面层性能参数如表4所示。试验加载采用力-位移混合控制的方案进行。即在墙体开裂前采用力控制加载,每级荷载加载一次;墙体开裂后改用位移控制加载每级荷载加载两次,直至荷载下降至极限荷载的85%停止加载。
2.2 破坏形态模拟对比分析
对于砌体开裂位移,试验取墙面首次出现肉眼可见裂缝时刻所处加载级的位移值。数值模拟模型采用式(3)计算所得砌体受拉损伤指标 DAMAGET来表征墙体裂缝分布和开展情况。钢板屈曲根据生死单元状态确定:第一阶段为弹性工作阶段,此时接触界面 Cohesive单元及焊口处生死单元均处于弹性受力状态,对应加固钢板小幅受力变形的弹性阶段;第二阶段为损伤累积阶段,此时接触界面Cohesive单元刚度开始损伤,焊口处生死单元达到折减强度,并开始产生塑性变形,加固钢板受力变形速率加快,但由于加固面层尚未失效剥离,此时钢板挠曲仍受约束;第三阶段进入失效阶段,此时接触界面Cohesive单元失效,粘结界面仅限提供正应力及摩擦力,而不再具有粘结性能,部分焊口处生死单元失效删除,加固钢板在竖向荷载及侧向应力的作用下趋于自由挠曲,并于钢板连接焊缝处进一步产生应力集中,继续引发其余焊口生死单元失效,此时对应加固钢板的挠曲及断裂失效阶段。
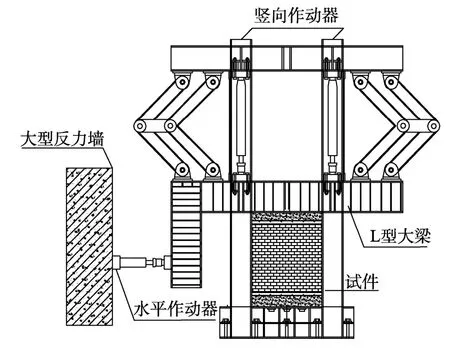
图6 试验加载装置布置Fig.6 Test loading device layout

图7 试验墙体示意Fig.7 Schematic of wall specimens

表2 墙体材料性能参数Table 2 Performance parameters of wall materials

表3 加固钢板性能参数Table 3 Performance parameters of reinforced steel plates

表4 聚合物砂浆面层性能参数Table 4 Performance parameters of polymer mortar layers
图8给出了加固砌体墙数值模拟与试验墙体主要破坏形态对比情况。由图8可知数值模型能够模拟出正交加固墙和斜撑加固墙的三阶段破坏特征:
1) 墙体中部首先出现斜裂缝,大致沿 45°方向延伸至墙体四角。此时模拟所得云图是据式(2)计算得到的,即采用砌体的受拉损伤值来表征裂缝开展。
2) 连接角钢与包角角钢连接处焊口断裂,加固扁钢产生不同程度屈曲,钢板失效。这一过程中,钢板焊口断裂对应生死单元失效移除时刻,即焊缝处生死单元应力达到文中所述折减强度后,进而产生塑性绝对变形位移达到0.5 mm的时刻。
3) 聚合物砂浆抹面与砌体脱粘,表征面层脱落失效,墙体最终破坏。此处砂浆面层脱粘剥离阶段对应文中所述接触界面处 Cohesive单元刚度开始损伤直至失效删除,此后界面仅存在摩擦力及正应力作用,即对应于文中图5(b)整体混合曲线的下降段,具体表达式参见式(11)。

图8 试验墙体主要破坏形态对比Fig.8 Comparison of main destruction forms of test walls
2.3 抗震性能模拟对比分析
2.3.1 正交加固墙
图9、图10和图11给出了不同砂浆强度下正交加固墙体滞回曲线、骨架曲线、刚度退化曲线模拟与试验结果的比较曲线。从图9~图11可以看出,本文数值模拟得到的滞回环、骨架曲线以及刚度退化曲线与试验结果基本一致。其中,对于BQ-3模型,下降段范围内数值模拟所得曲线与试验相应曲线相差较大,主要是荷载进入下降段后测试墙顶的位移计超量程进行更换导致的试验误差引起的。
2.3.2 斜撑加固墙
图12给出了砂浆为M1.0情况下斜撑加固墙体的滞回曲线、骨架曲线以及刚度退化曲线模拟与试验结果的对比曲线。由于各砂浆强度下所得曲线趋势基本一致,这里仅给出M1.0情况。

图9 正交加固墙数值模拟与实际试验滞回对比曲线Fig.9 Comparison of hysteresis curves between numerical simulation and actual test of orthogonally reinforced walls

图10 正交加固墙数值模拟与实际试验骨架对比曲线Fig.10 Comparison between numerical simulation and actual experimental skeleton curves of orthogonally reinforced walls

图11 正交加固墙数值模拟与实际试验刚度退化对比曲线Fig.11 Comparison curves between numerical simulation andactual experimental stiffness degradationof orthogonally reinforced walls

图12 XBQ-1数值模拟与实际试验对比曲线Fig.12 Comparison curves between XBQ-1 numericalsimulation and actual test
2.4 性能指标模拟对比分析
为定量评估本文所述模型的模拟精度,现将加固砌体的有限元计算结果同试验数据作对比分析,抗震性能指标及误差计算结果参见表5。
由表5可知,抗剪承载力和峰值位移两项指标的模拟效果最佳,相对误差绝对值的平均值分别为7.9%和8.6%。其中BQ-1和XBQ-4误差稍大,分别为11.5%和18.5%。能量耗散系数和初始刚度两项指标的相对误差绝对值的平均值分别为10.6%和12.0%。延性系数、极限位移和开裂位移的模拟相对误差绝对值的平均分别为 13.9%、13.9%和16.2%。注意到误差最大的指标位于 BQ-1开裂位移、BQ-3极限位移和 XBQ-3极限位移,分别达34.9%、-48.5%和-33.8%。分析位移相对误差较大的可能原因有两点:一是试件开裂时刻的视觉判定存在误差;二是试验分级加载制度过程中量测器材捕捉开裂和极限位移会存在滞后性。此外,延性系数又由开裂位移和峰值位移计算得出,这一过程中亦会产生误差累积。
整体来说,本文所述模型各项指标模拟效果良好。虽有个别项偏差稍大,但考虑到砌体材料、试验结果离散性等因素的影响。统计显示所有墙片的全部指标中有81%的误差在20%以内。

表5 墙体性能指标模拟值与试验值对比Table 5 Comparison of simulated and test values of wall performance indexes
3 结论
本文采用 ABAQUS有限元软件,在砌体整体式模型的基础上结合分离式思想提出了组合材料加固砌体的数值建模方法,并与已有试验成果进行了对比分析。现总结如下:
(1) 8片加固砌体墙片数值模拟和试验结果对比分析表明,采用本文提出的数值模拟方法能够很好地模拟出组合加固砖砌体墙片的破坏形态、滞回性能,是可行的,可用于组合材料加固砌体抗震性能的进一步变参数数值模拟研究。
(2) 数值模拟所得加固砌体墙片的滞回曲线、骨架曲线和刚度退化曲线与试验曲线基本吻合,主要破坏形态与试验一致,能够良好模拟出加固墙体的抗震性能和破坏特征。
(3) 数值模拟所得抗剪承载力、峰值位移两项指标的模拟效果最佳,大部分墙体误差在 7.6%以内,只有BQ-1和XBQ-4误差稍大,分别为11.5%和18.5%。能量耗散系数和初始刚度指标的模拟效果良好,相对误差绝对值的平均值分别为10.6%和12.0%。而延性系数、极限位移和开裂位移三项指标模拟误差稍大,相对误差绝对值的平均分别为13.9%、13.9%和16.2%。但总体而言,其具有重要参考价值。

