基于优先级顺序的进气凸轮型线优化分析
曹睿鑫,许俊峰,王步云,侯 健,张艳岗
(中北大学能源动力工程学院,山西 太原 030051)
伴随着我国汽车保有量的增加,由此导致的一系列环境、能源、交通等矛盾冲突日益突出[1],这要求汽车发动机向着高速、高强度、低排放的方向发展。因此,提高发动机配气机构的可靠性迫在眉睫。配气机构是发动机的重要组成部件,关系到发动机的动力性和可靠性。配气机构一般由配气凸轮驱动,而凸轮型线的好坏直接决定了配气机构和发动机的性能指标。在对凸轮进行分析时出现的问题往往不止一个,而不同问题对配气机构的影响大小不一,因此本文提出一种基于优先级顺序的优化策略,利用AVL-EXCITE Timing Drive对凸轮型线进行分析与优化。
1 配气机构建模及分析
1.1 配气机构模型建立
在AVL-EXCITE Timing Drive软件中,运动学、动力学分析是基于多质量动力学模型的理论,并以一定的集中质量进行简化[2]。根据原配气机构布置,用AVL-EXCITE Timing Drive分别建立运动学与动力学分析模型,如图1和图2所示,建立模型后需定义零件质量、刚度、阻尼等参数。
1.2 原配气机构分析
1.2.1原配气机构运动学分析
将原进气凸轮型线导入运动学模型中,并在模型中进行参数的仿真,得到进气阀的运动学参数,如表1和图3所示。
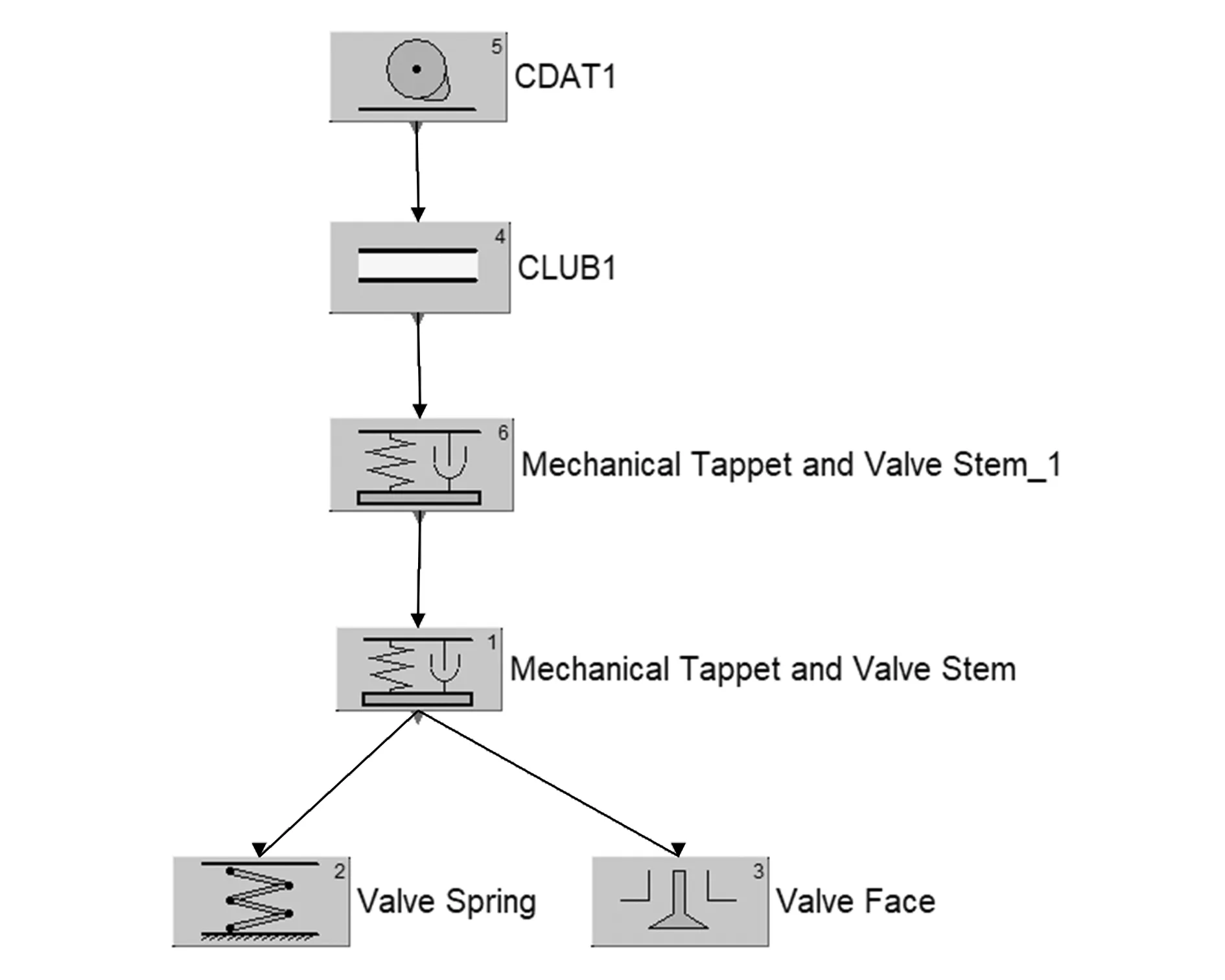
图1 配气机构运动学模型
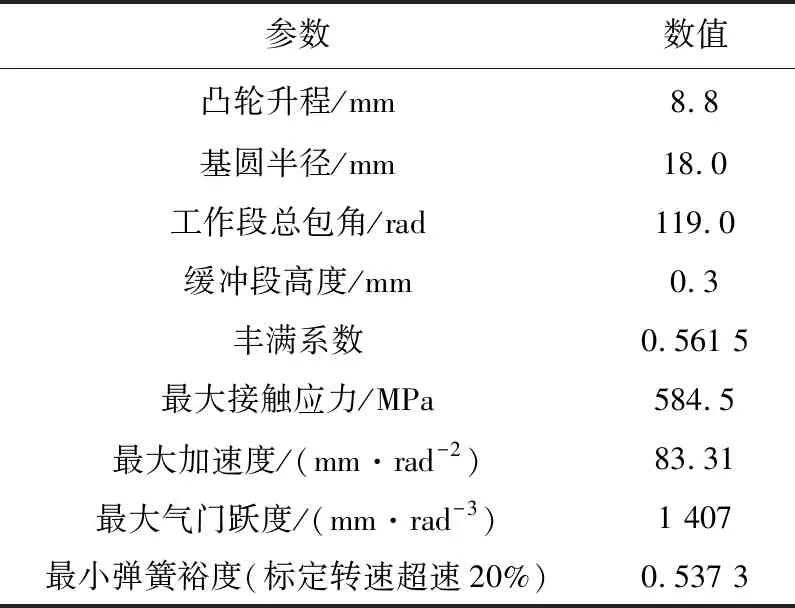
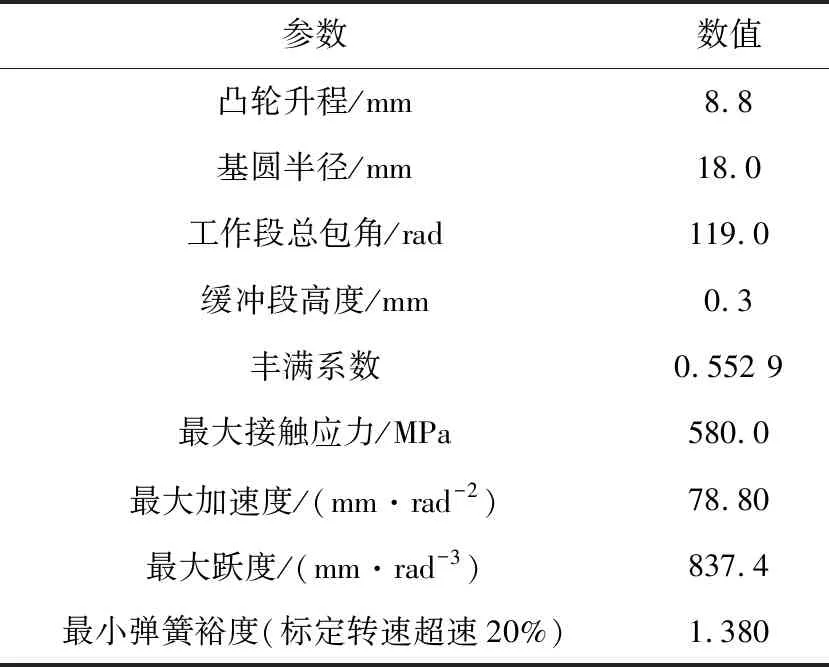
表1 原配气机构运动学主要参数
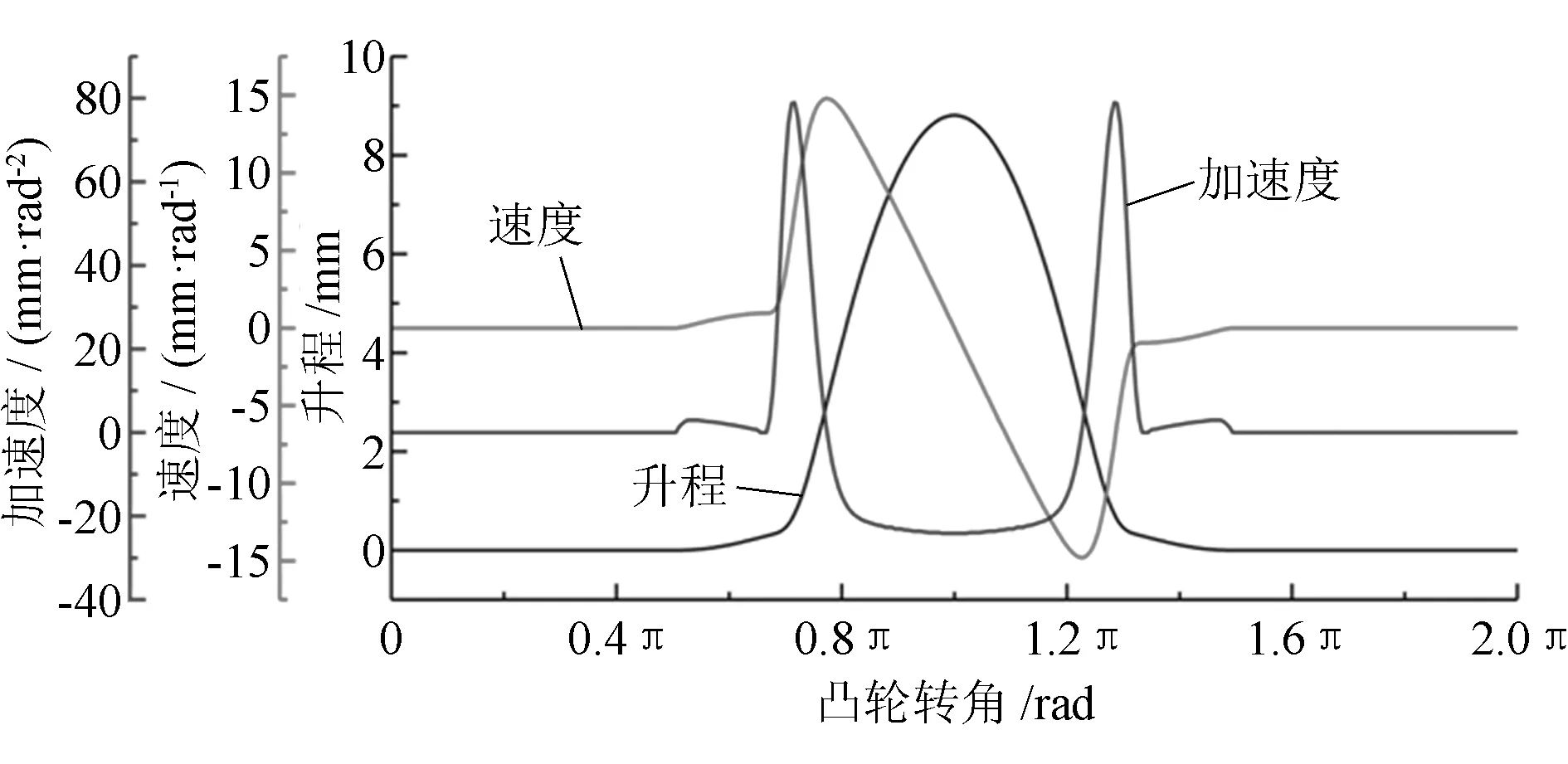
图3中进气凸轮的升程曲线较为平滑,但是速度和加速度曲线则出现了曲折,其中加速度曲线的起伏非常明显,这将导致凸轮的跃度急剧变化,气门最大跃度值过高。

图2 配气机构动力学模型

图3 凸轮升程、速度、加速度曲线
气门跃度是表示气门加速度变化缓急与否的参数,可以用来衡量凸轮和从动件之间的接触是否平稳。气门跃度通常小于1 000 mm/rad3[3],过大的气门跃度值会导致气门冲击,产生振动和噪声,不仅会导致发动机早期疲劳损伤,而且会严重影响流动特性。
在设计时要求气门弹簧的弹簧裕度留有合适的剩余量。裕度过小时,在发动机运转过程中从动件会与凸轮分离,产生飞脱;裕度过大时,会导致驱动功率过大,造成配气凸轮严重磨损。因此要求弹簧裕度的范围为1.25~1.60[4-5]。从表1中可以看到,原配气机构在超过标定转速20%的情况下最小弹簧裕度远小于基本要求。
为提高换气效率,凸轮型线应具有较高的丰满系数,一般丰满系数要求大于0.5[6]。原机丰满系数基本满足设计要求,但相对较低。原机凸轮与挺柱材料分别为钢与冷铸铁,其允许的最大接触应力为650 MPa,满足许用值要求。
1.2.2原配气机构动力学分析
本文在进行运动学分析时,将配气机构看作刚体,忽略了运动过程中各因素的弹性变形,造成高速时速度和加速度畸变,不利于配气机构的分析和优化。在高速工况下(本文仅分析6 000 r/min这一种高速工况),对原配气机构进行了动力学分析,部分结果如图4和图5所示。
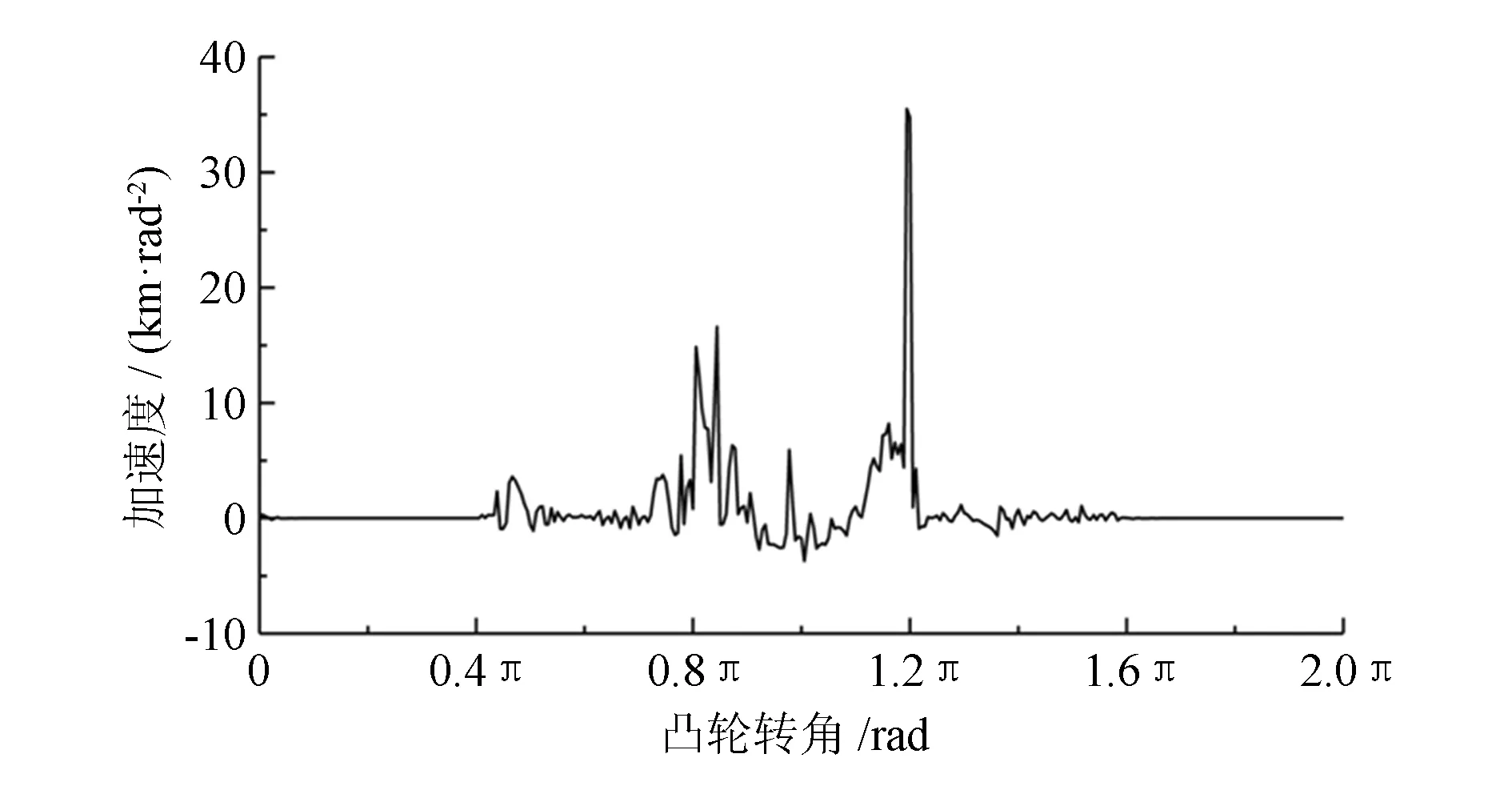
图4 基于动力学的加速度曲线

图5 基于动力学的接触应力曲线
从图4可以看到,凸轮的加速度曲线极不稳定,导致产生过大的跃度,从而产生较大的振动和噪声;从图5可以看到,最大接触应力为811.5 MPa,超过了材料允许的最大接触应力,在工作过程中周期性接触应力的反复作用下,将引起零件的较大磨损,从而导致凸轮与从动件之间的接触面损坏。
2 凸轮优先级顺序设计与优化
2.1 优先级顺序方案的设计
综上所述,对原配气凸轮进行运动学和动力学分析后,发现原配气机构凸轮型线存在严重缺陷,不能很好地满足配气机构的工作要求,因此需要对原进气凸轮型线进行合理优化。由此本文提出一种基于优先级顺序的凸轮型线优化方案。
1)凸轮与从动件之间的接触应力大小直接影响凸轮机构的寿命,由此可知,为了增加凸轮机构的使用寿命必须减小凸轮与从动件之间的接触应力。因此,将凸轮与从动件之间的接触应力定为第一优先级。
2)气门跃度是衡量凸轮和从动件间接触是否平稳的主要参数,一般认为气门跃度值越小越好,这样会使得气门运动更加平稳,从而使发动机进气行程更加顺畅。因此,将气门跃度定为第二优先级。
3)为使配气机构有良好的动力性能、工作时不发生过高的振动和噪声,要求配气机构加速度峰值的绝对值不能过大,从而提高配气机构的高速性能[7]。因此,将凸轮加速度定为第三优先级。
本文基于上述优先级顺序方案的设定,针对原配气机构出现的各种问题,对原配气机构的凸轮型线进行优化设计。
2.2 缓冲段设计
缓冲段是在凸轮基圆与工作段之间的过渡段。余弦缓冲段相对容易设计,且在缓冲段结束处加速度为零,能够实现和工作段加速度的平稳过渡,从而可以最大程度地保证配气机构的可靠性和稳定性。因此,新设计的凸轮型线采用余弦函数设计,气门落座速度为300 mm/s。余弦段的升程曲线函数方程为:
h=h0(1-cos(t·α)) 0≤α≤α0
(1)
式中:h为气门升程;α为凸轮轴转角;α0为缓冲段包角;h0为缓冲段升程;t为时间。
余弦缓冲段和工作段加速度曲线保持着连续性,对配气机构的可靠性和稳定性有较大的保障。
2.3 工作段设计
在工作段设计中,需要结合发动机自身条件,结合上述缓冲段的设计方式,采用多项式高频函数方法,设计出完整的凸轮型线。
气门升程函数为:
h=h(α)=(hmax-h0)(1+C2x2+C4x4+Cpxp+Cqxq+Crxr+Csxs)
(2)
(3)
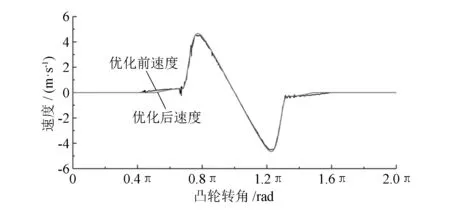
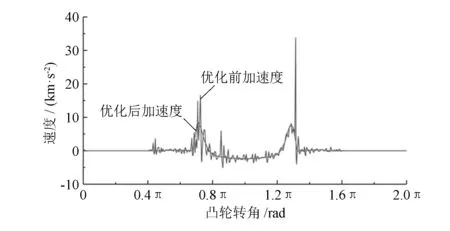
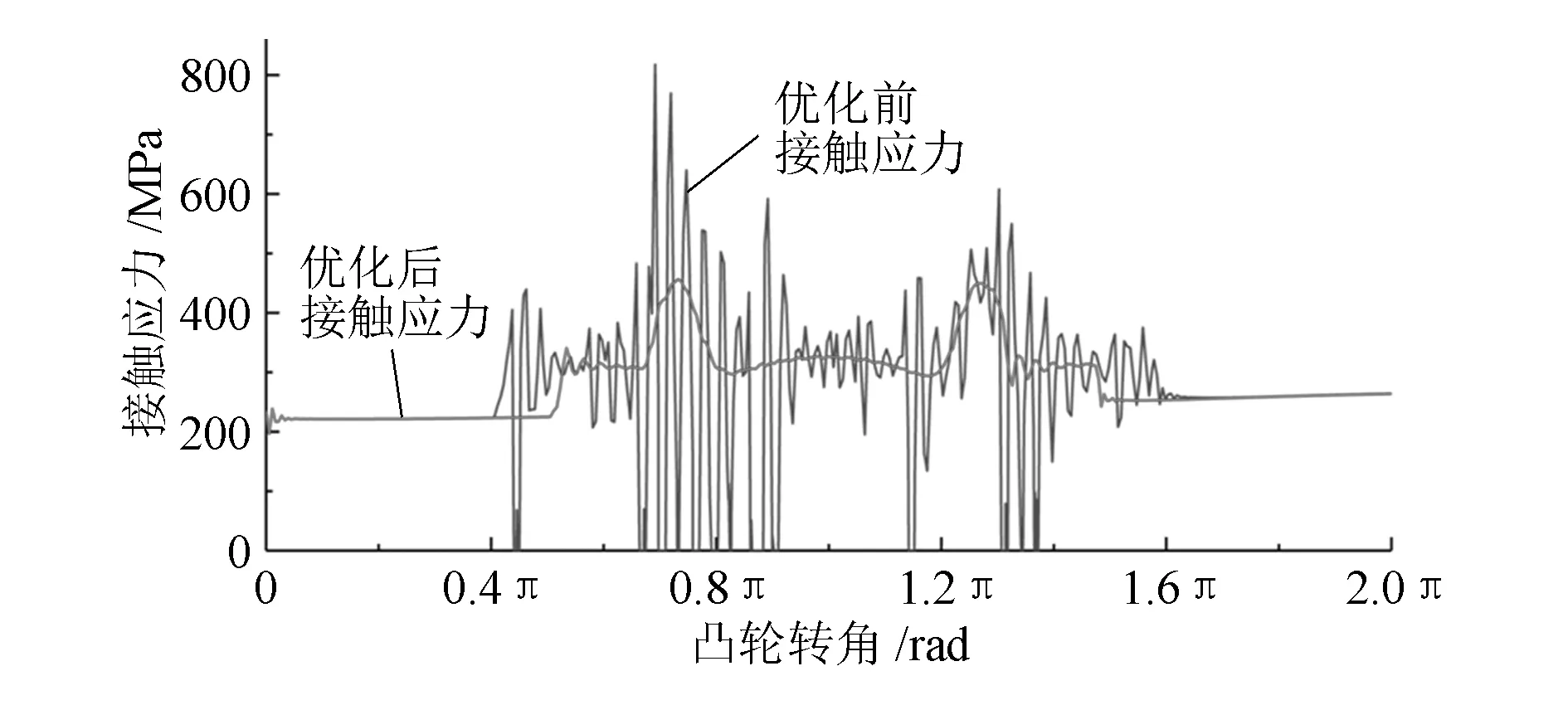
式中:hmax为气门最大升程;C2,C4,Cp,Cq,Cr,Cs为常数,其中p,q,r,s为偶数,且p 函数满足5个边界条件[8]: 1)当α=α0时,x=1,h=0,有 1+C2+C4+Cp+Cq+Cr+Cs=0 (4) 2C2+4C4+pCp+qCq+rCr+sCs=VR (5) 2C2+12C4+p(p-1)Cp+q(q-1)Cq+r(r-1)Cr+s(s-1)Cs=0 (6) p(p-1)(p-2)Cp+q(q-1)(q-2)Cq+r(r-1)(r-2)Cr+s(s-1)(s-2)Cs=0 (7) 5)当α=αB时,有 h(αB)=hmax (8) 联立方程(4)~(8),即可得到关于未知量Cp,Cq,Cr,Cs的方程组。系数C2,C4一般取0.1或0.2,而p,q,r,s可以根据经验公式[9]取值:p=2~20,q=2n,r=2n+2m,s=2n+4m,其中m,n为一定范围的正整数,通常m=2~9,n=3~10。 在优化设计中,考虑到各优先级参数对凸轮型线的影响程度大小,以凸轮和从动件之间的最大接触应力、凸轮的曲率半径和最小弹簧裕度为限制条件,结合上述凸轮型线函数的选取,将凸轮允许的最大跃度值、凸轮加速度最大峰值定为优化目标,经过多次调整,最终得到优化后的凸轮型线。 本文基于优先级设计原则,综合考虑各参数对配气凸轮的影响因素后,设计得到优化后的凸轮型线,并将优化后的凸轮型线在运动学模型中进行仿真,得到进气阀的运动学参数,如表2和图6所示。 表2 优化后的配气机构运动学主要参数 图6 优化后的凸轮升程、速度、加速度曲线 由仿真结果可知,新得到的凸轮气门升程、速度、加速度曲线都有比较光滑的过渡,较为稳定。优化后的气门跃度较原凸轮的跃度降低了40.5%,小于允许最大值1 000 mm/rad3,且没有较大的突变,说明凸轮和从动件运动平稳,没有太大振动,确保配气机构具有较为理想的运动特性。 优化后的凸轮型线在发动机转速为7 200 r/min(超标定转速20%)的情况下气门弹簧裕度显然处于许可范围内,情况比较理想。 将优化后的凸轮型线进行动力学仿真,优化前后凸轮升程曲线对比如图7所示,凸轮速度、加速度曲线对比如图8、图9所示。由图可知:优化后的凸轮型线比较平滑,说明气门的开启和关闭情况比较理想;优化后的速度曲线几乎无波动,说明气门落座时没有跳动;优化后的凸轮加速度曲线较为平顺,没有过大的波动。 图7 优化前后凸轮升程曲线 图8 优化前后凸轮速度曲线 图9 优化前后凸轮加速度曲线 从图10可得:优化后的凸轮与从动件之间最大的接触应力降为488.5 MPa,相比于原配气机构降低了39.8%,凸轮与从动件始终保持紧密接触,没有出现接触应力为0的情况,也没有产生飞脱现象。 图10 优化前后配气机构接触应力曲线 本文采用优先级顺序优化方案对原配气凸轮进行多项式高次方优化设计,利用AVL-EXCITE Timing Drive进行仿真分析,并将优化后的凸轮型线与原机运动学与动力学特性进行对比,结论如下:优化后,处于各优先级顺序的凸轮参数都有了显著改善,其中凸轮与从动件之间的最大接触应力比原来降低了39.8%,凸轮跃度降低了40.5%,有效地降低了凸轮与从动件之间的振动,保证了配气机构的平稳运行,而且优化后弹簧裕度仍然处于允许的范围内,提高了配气机构的可靠性。仿真分析得到的结果为凸轮型线优化提供了可靠的理论基础,因而后续工作将尽可能多做试验,以进一步完善相关理论。
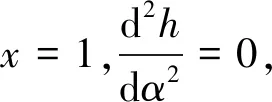
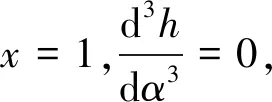
3 优化后的配气机构分析
3.1 优化后的配气机构运动学分析
3.2 优化后的配气机构动力学分析

4 结论

