住房价格、资本投资与工业部门资源配置效率
纪建悦 周婧琳 褚磊

摘 要:本文基于成本前沿理论对配置效率的分解,测算了工业部门的资源配置效率。在此基础上,选取资本投资为中介变量,利用2001—2017年我国30个省份的面板数据,采用系统GMM方法,运用逐步回归的中介效应分析模型就住房价格对工业部门资源配置效率的影响进行了实证分析。研究发现,住房价格通过“抽血效应”对实体经济资源配置效率产生显著的负向冲击,资本投资在其中起到了显著部分中介效应。
关键词:住房价格;资本投资;工业部门资源配置效率;中介效应;系统GMM
中图分类号:F830.9 文献标识码:A 文章编号:1674-2265(2020)12-0003-11
DOI:10.19647/j.cnki.37-1462/f.2020.12.001
一、引言
目前,我国经济发展进入调整期,经济增速放缓,主要依靠资源投入拉动经济增长的粗放型增长模式已经不再适用。要保持经济的持续健康发展,需要在既定的资源约束下提高资源的使用效率,这一方面依赖于技术水平的提升,另一方面也依靠资源配置的优化(陈永伟和胡伟民,2011)[1]。如果我国的资源配置效率可以达到美国的水平,则TFP将提高30%—50%,若不存在资源错配,总产出将提高110%(Hsieh和Klenow,2009)[2]。因此,提高资源配置效率对经济增长至关重要。学者们进一步对影响资源配置效率的因素进行了探究(丁志国等,2012;邵宜航等,2013;张建华和邹凤明,2015)[3-5]。在宏观层面,Restuccia和Rogerson(2008)[6]、陈永伟和胡伟民(2011)[1]、Brandt(2013)[7]等都认为要素市场和产品市场相对价格扭曲是造成资源配置效率下降的主要原因;张佩和马弘(2012)[8]、张庆君(2015)[9]和Midrigan等(2014)[10]认为信贷市场缺陷,即金融市场扭曲也是影响资源配置效率的重要因素;同时,产品替代性、调整成本的存在会加剧资源错配程度(孙浦阳等,2013;杨光等,2015)[11,12];周黎安等(2013)[13]、韩剑和郑秋玲(2014)[14]、靳来群等认为政治周期、政府干预、行政垄断是影响资源配置效率的重要渠道。而在微观企业层面,陈艳利等基于信息不对称和委托代理理论分析了企业集团内部交易与资源配置效率的关系,指出关联担保和内部交易会降低资源配置效率(陈艳利等,2014)[16]。
自1998年我国全面推行住房商品化后,特别是2003年以来,住房价格快速上涨。从2003年到2018年,全国平均商品房销售价格从2359元/平方米上涨到8736.9元/平方米,增长了3.7倍。许多学者针对房价与实体经济的关系展开研究,有学者认为房价上涨带来房地产市场的繁荣,同时带动了房地产相关行业的发展,推动了经济增长(梁云芳,2006)[17];但也有学者认为房地产行业过快发展会挤压实体经济,阻碍经济的长期稳定增长。此外,冯玉梅和杨瑞桐就不同地域展开研究,认为金融资源投入具有房地产业比较优势的城市能够促进当地经济增长,而投入房地产业比较劣势的城市则不利于当地经济增长(冯玉梅和杨瑞桐,2018)[18]。Han和Lu(2017)[19]则在行业层面进行分析,证实高房价抑制了制造业企业的生产性投资,进而对中国实体经济部门产生显著影响。上述文献从不同角度阐释了房地产迅猛发展对实体经济的影响,揭示了房地产过度繁荣的双面效应。
由于房地产兼具实物资产和虚拟资产的双重属性,我国城市房价持续高企,房地产投资额占社会固定资本投资额的比重亦逐年攀升,部分学者开始注意到房地产过度繁荣与资源配置效率的关系。陈斌开等认为,高房价导致资源错配,降低资源再配置效率,進而降低全要素生产率,阻碍中国经济的持续稳定增长(陈斌开等,2015)[20]。张巍和许家云等认为,高房价引致的工资上涨导致了我国过度的资本深化和过快的产业升级,并降低了地区的资源配置效率(张巍等,2018)[21]。罗双成和陈卫民利用中介效应模型检验房价上涨通过要素错配影响城市创新能力的作用机制,认为房价上涨过快导致资源错配,造成资源配置效率的损失,是抑制城市创新能力的重要原因(罗双成和陈卫民,2019)[22]。另外,房地产投资对实体经济资源配置效率的影响机理也逐渐成为学术界争论的热点。罗知和张川川(2015)[23]考察了房地产投资对制造业资源配置效率的影响,发现国有企业获得大量信贷资源并投资于房地产是造成制造业资源配置效率下降的原因之一。余永泽和李启航(2019)[24]认为,城市高房价显著抑制了城市全要素生产率水平的提升,而这种抑制效应主要来自房地产投资对实体经济资金的“挤占效应”和“资源错配效应”。徐妍和郭品(2019)[25]提出,我国房地产定价中的非效率因素是近年来房价持续上涨的重要原因,且会引起资本市场和劳动力市场的资源错配。
由文献梳理可知,现有相关研究还存在一些可拓展空间:现有文献针对住房价格影响实体经济的研究,特别是在房价影响配置效率的作用路径方面仍存在争议,且鲜有学者将住房价格、工业部门资本投资和资源配置效率纳入同一框架下构建数理模型进行实证分析;此外,现有研究大多利用TFP的离散程度衡量资源配置效率,而计算TFP时的诸多假设降低了计算结果的准确性。为此,本文以地区资本投资为切入点,选取工业部门新增固定资产投资为中介变量,主要考察在该中介效应下,住房价格快速上涨对工业部门资源配置效率的影响。本文研究对新时期进一步提高工业部门资源配置效率、促进经济增长具有重要的理论价值和现实意义。
二、影响机理分析
(一)工业部门资源配置效率测算
Farrell(1957)[26]首次以直观图(见图1)的形式提出成本效率的概念,并将前沿分析方法引入到效率研究中来,形成最初的成本前沿理论。该理论认为成本效率可以分解为技术效率和配置效率。其中,配置效率衡量的是在当前的投入价格水平下,决策单元实现投入最优组合的能力,本文用图1对配置效率进行说明。假设决策单元使用两种投入,分别为劳动力与资本,生产一种产出y。等产量线L(y)为生产y所需的最少要素投入组合。PP为决策单元的一条成本线,PP与L(y)相切于a点。当决策单元的投入组合为a点时,能以最小的成本生产y,配置有效。若决策单元的投入组合在a点的左侧,说明相对于劳动力来说,资本投入过少;若决策单元的投入组合在a点的右侧,则说明相对于劳动力来说,资本投入过多。以上两种情形都是配置非有效的。当决策单元的投入组合在b点时,配置效率(AE)可以表示为:
[AE=od/ob]
当决策单元的投入组合为c点时,不仅存在配置非有效,而且存在技术非有效。由于本文主要讨论资源配置效率,因此在分析中假设决策单元都是技术有效的。
快速上涨的住房价格给房地产业带来了高额的回报。按照吕江林(2010)[27]的计算方法,2018年房地产企业的平均成本费用利润率为14.2%,而工业企业仅为6.9%。房地产业的高回报率吸引了大量投资,2003—2018年该行业投资规模年均增长率为15.82%。房地产过度投资会对工业部门的资金产生“抽血效应”,从图2可以看出,当房地产投资迅速膨胀,投资增长率上升时,工业新增固定资产投资增长率下降,二者呈现明显的负相关关系。
高房价给房地产带来高回报,高回报使得房地产投资迅速增加,房地产业成为巨大的“吸金池”,对工业部门的资金产生巨大的吸附作用,形成对工业部门的“抽血效应”。假设短时期内,劳动力供应充足,劳动力和资本的价格保持不变,则房地产对工业资金的“抽血效应”会使得工业部门资源配置效率下降。具体分析如下:
对于初始配置有效的决策单元,由于“抽血效应”的存在,一方面,其没有充足的资金,无法扩大生产规模,提高市场占有率,挤出低效决策单元,从而失去了进一步提高资源配置效率的机会;另一方面,由于投资的“理性选择”,决策单元倾向于将稀缺资源投入到高回报率的房地产业,减少主要业务的资本投入。在产出y一定的情况下,资本投入减少,使得投入组合由图1中的a点向b点移动,即配置效率下降。
对于初始配置非有效的决策单元,如图3所示。若决策单元的初始投入组合为(a)图[OO1],即相对于劳动力来说,资本投入过少。那么,当整体工业资本投入减少或决策单元将资本投向房地产业时,投入组合由[OO1]向[OO2]方向移动,组合中的资本投入进一步减少,配置效率进一步降低。若决策单元初始投入组合为(b)图[OO3],即相对于劳动力来说,资本投入过多。这时,当整体工业资本投入减少或决策单元将资本投入房地产业时,投入组合由[OO3]向[OO4]方向移动,配置效率改善。但如果房价进一步上涨,房地产业的利润率进一步提升,资本进一步抽离工业部门,决策单元将更多的资本投向房地产业,投入组合由[OO4]向[OO5]方向移动,相对于劳动力来说,资本投入过少,配置效率下降。
因此,“抽血效应”使得初始配置有效决策单元的配置效率下降,而对于初始配置非有效的决策单元,不管劳动力和资本的投入比例如何,其配置效率最终都趋于降低。同时,“抽血效应”使得工业部门的资本投入迅速减少,而短时间内,劳动力的数量却不会发生太大的变化,这种相对供求关系的变化,必然会引起要素价格的相对扭曲,而要素价格相对扭曲正是导致资源配置效率下降的主要原因(谢攀和林致远,2016)[28]。
(二)住房价格对资源配置效率的影响路径
房价快速上涨作为一种产品市场的相对价格扭曲,会导致资源错配,进而降低资源配置效率,最终损害TFP的增长(罗双成,陈卫民,2019)[22]。一方面,房地产行业的发展会削弱个体的创业行为,对创业活动具有挤出效应,而且住房价格是产生挤出效应的主要原因(林嵩,2012)[29]。另一方面,高房价会对企业的创新活动产生阻碍(张杰等,2016)[30],高回报率吸引了大批企业携带大量资金进入房地产业,遏制了企业创新,从而削弱了实体经济发展(王文春和荣昭,2014)[31]。房地产市场迅猛发展使房地产企业获利丰厚,并吸引了越来越多的资金涌入房地产领域。在金融资源有限而房地产高回报率的情况下,工业部门资本投资重心转移,使金融资源过度配置到房地产行业而挤占本行业的投资,使高效率的企业缺乏资金用于扩大生产规模、提高市场占有率和挤出低效率企业。同时,房地产价格上升会使工业企业经营成本增加、利润压缩,资金进一步退出实体经济。因此,房地产投资挤出工业部门投资后会使其资源配置效率下降,该挤出效应容易导致经济结构失衡,是长期经济发展的潜在风险。
综合上述分析,本文认为:住房价格高企,房地产投资额占比攀升,会通过“抽血效应”吸纳大量工业部门资本投资资金,进而导致其资源配置效率下降。
三、研究设计
(一)数据来源与变量定义
1. 数据来源。基于数据的可获得性,本文选取我国30个省份2001—2017年的相关数据进行工业部门资源配置效率的测算及中介效应分析。
在工业部门资源配置效率测算部分,工业企业就业人数和工业就业人员平均劳动报酬数据来自《中国劳动统计年鉴》,固定资产净值、固定资产折旧和工业增加值数据来自《中国统计年鉴》。在中介效应分析部分,各省份商品房销售价格、进出口总额、财政支出与财政收入数据来自《中国统计年鉴》,工业部门新增固定资产投资数据来自《中国固定资产投资统计年鉴》,工业国有企业比重数据来自《中国工业统计年鉴》。由于年鉴中部分数据缺失,采用插值法对2001年、2002年和2013年的工业部门新增固定资产投资数据进行处理。相关变量名义值均用价格指数進行处理,以消除通货膨胀的影响。其中,劳动报酬、商品房销售价格和进出口总额采用分省CPI指数进行处理,固定资产净值与工业部门新增固定资产投资采用固定资产投资价格指数进行处理,工业增加值采用工厂生产者出厂价格指数处理,各指数均以2000年不变价平减。
2. 变量定义。
(1)工业部门配置效率测算。选取工业企业就业人数和固定资产净值为投入指标,工业增加值为产出指标。以工业企业就业人员平均劳动报酬作为劳动力的价格,以当年固定资产折旧与固定资产净值的比值作为固定资产的价格(杨大强和张爱武,2007)[32]。其中,当年固定资产折旧等于本期累计折旧与上期累计折旧的差值。由于在进行固定资产出售、清理、处置的会计处理时,必须将原来提取的固定资产累计折旧转出,所以可能会出现减少本期累计折旧的现象,这时,以本期累计折旧减去上期累计折旧计算的当年折旧额会出现负数,以此折旧额计算的固定资产价格小于零,这与现实情况不符。因此,对于固定资产价格小于零的数据,本文用相邻两期固定资产价格的平均值作为本期的固定资产价格。指标具体计算方法见表1。
(2)中介效应分析。将工业部门资源配置效率作为被解释变量,住房价格作为主要解释变量,选取工业部门新增固定资产投资作为资本投资的替代指标,即中介变量。此外,工业部门的资源配置效率还受到许多其他因素的影响,如要素价格、金融发展水平、政府干预等。本文选取的控制变量主要有三个:
首先,一个省份的国有企业比重会影响该省份工业部门的资源配置效率,因为国有企业更容易以较低的成本从银行获得贷款,其投资方向会对工业部门资源配置效率产生影响。若国有企业将以较低成本获取的信贷资源投向资源配置效率较低的行业,如房地产业,则会降低工业部门的资源配置效率。因此,本文以国有企业比重(国有工业企业就业人数/工业总就业人数)作为控制变量。
其次,一个省份的贸易发展水平也会影响该省份工业部门的资源配置效率。由于贸易发展程度越高的省份竞争会更加激烈,激烈的竞争可以提高资源的配置效率,使二者呈现正向促进关系。鉴于地区的贸易发展水平与其进出口总额往往正相关,故本文选取进出口总额作为控制变量。在数据处理时,先利用各年汇率将进出口总额统计单位由“千美元”换算为“人民币”,再使用分省CPI指数对名义进出口总额进行调整。
最后,在以经济指标为主要政绩考核指标的背景下,政府有直接干预经济建设的动机,表现为扩大财政支出的冲动(靳来群等,2015)[15]。一方面,政府干预经济很可能会进一步加大要素市场和产品市场相对价格的扭曲程度,从而加剧资源错配,降低资源配置效率;另一方面,政府干预经济可以弥补社会投资的不足,使得工业部门有机会获得足够的资本来提高资源配置效率。因此,本文以财政激励((財政支出-财政收入)/财政收入)作为控制变量。
(二)模型构建
1. 工业部门资源配置效率测算方法。在测算资源配置效率时,现有文献大多采用HK方法。[2]使用该方法测算配置效率时,需要对生产函数形式进行设定,且存在许多假设条件,但设定的函数形式和某些假设条件很可能与现实情况不符,从而降低测算结果的准确性。为解决以上问题,本文采用DEA窗口分析法(DEA Windows Analysis)测算工业部门的资源配置效率。
DEA方法构造出一个非参数的包络前沿面,位于前沿面上的点有效,位于前沿面下的点无效。假设有N个决策单元(DMU),每个决策单元使用K种投入生产M种产出,第i个决策单元的效率值就是求解以下线性规划:
一般的DEA方法主要用于测算截面数据的效率值,而不能直接用于面板数据的分析,而且用截面数据测算的效率值不能直接用于跨时期的比较(盛鹏飞,2015)[33]。为克服以上缺陷,凯诺斯等提出了DEA窗口分析法,该方法利用移动平均的原则,将同一决策单元在不同时期作为不同的决策单元进行效率测算(Charnes等,1985)[34]。假设有N个决策单元、T个时期的面板数据,首先将其分成若干个子面板数据,每个子面板数据包括L个时期,L一般为3(Sufian,2017)[35]。这样,每个子面板数据就形成了一个窗口,共有T-L+1个窗口,其次利用每个窗口构建前沿面:
最后,将每个决策单元同一时期不同窗口的效率值进行平均,得到该决策单元的最终效率值。当外部冲击使得前沿面剧烈变动,从而导致同一时期不同窗口的效率值发生显著差异时,可以采取剔除异常值的方式得到更加有效的评价值(盛鹏飞,2015)[33]。本文首先通过投入变量及其价格以及产出变量,测度各省份2001—2017年的成本效率(CE),再剔除价格因素进一步测算得到综合技术效率(TE),最终计算二者之比得到各省份各考察年度的配置效率(AE)。
2. 中介效应模型。经典的中介效应检验方法是Baron和Kenny(1986)[36]提出的依次检验法,变量之间的关系如下:
在式(10)—(13)中,[AEit]和[AEit-1]为被解释变量,即当期和滞后一期的工业部门的资源配置效率;[Priceit]表示主要解释变量即住房价格;[NIit]和[NIit-1]表示中介变量,即当期和滞后一期的工业部门新增固定资产投资;[Zit]表示影响资源配置效率的三个控制变量,即国有企业比重([Stateit])、贸易发展水平([Tradeit])和财政激励([Financeit]);[μit]为干扰项。
在模型中引入滞后的被解释变量会导致内生性问题,解释变量可能与扰动项相关也会产生内生性问题。当存在内生性问题时,采用传统固定效应或随机效应的OLS估计得到的估计量是有偏的。同时,上述式(10)并没有消除未观察到的省际区域效应,阿雷利亚诺等提出采用广义矩估计(GMM)方法解决以上问题(Arellano和Bond,1991)[37],做一阶差分可消除省际效应:
但在(14)式中,[ΔAEit-1]与[Δεit]依然相关,为此,必须采用工具变量进行估计,也被称为差分GMM。布伦德尔等将差分方程与水平方程作为一个方程系统进行GMM估计,称为系统GMM(Blundell 和Bond,1998)[38]。与差分GMM相比,系统GMM可以提高估计效率,使得估计结果更为可靠(钱学锋和陈勇兵,2009)[39]。因此,本文将采用系统GMM方法就住房价格对工业部门资源配置效率的影响进行实证分析。
中介效应的检验方法众多,且在统计检验功效方面各有优劣。本文采用温忠麟和叶宝娟(2014)[40]提出的修正后的中介效应检验方法,以Bootstrap法来替代Sobel检验。检验流程图见图4。
四、工业部门资源配置效率测算
(一)描述性统计
表2报告了工业部门的资源配置效率测算中主要变量的描述性统计结果。附加相应的劳动力价格和固定资产价格,用以计算工业部门的资源成本效率。
(二)测算结果
本文运用MaxDEA软件进行效率测算。综合考虑可信度和稳定性因素后,将窗口宽度选择为3,共有15个窗口。窗口分析中,每一列数值反映了同一窗口内,同一省份效率值随时间的变化趋势;每一行则为各省份同一时期(每年)在不同窗口下的效率值。具体测算中,先基于传统CCR模型下的窗口分析方法,测算得到各年各省份的成本效率值(CE)和综合技术效率值(TE),将各时期各窗口的均值作为各省份在该时期的最终效率值,以体现效率值测度的稳定性,再将成本效率和技术效率的比值作为各省份各时期的配置效率值(AE)。
考虑到篇幅的限制,本文只列出了上海、江苏、广东、宁夏、青海和贵州六个省份测算的效率,具体值见表3、表4。其中,宁夏、青海和贵州为欠发达地区的代表,上海、江苏和广东为发达地区的代表。从表3中可以看出,从时间层面上来看,不管是发达地区还是欠发达地区,在2008年前后各省份工业部门的资源配置效率都出现较大的变化。在2008年之前,各省工业部门的资源配置效率相对较高;而2008年之后,各省工业部门的资源配置效率在波动中有所下降。以宁夏为例,2001年其工业部门资源配置效率为0.651845,到2008年波动至0.894182,但到了2017年又下降至0.587632。与工业部门资源配置效率情况类似,2008年也是我国住房价格变动的转折年,房价从2003年开始迅速上涨,在2008年经历了短暂的下跌之后,在2009年又开启了新一轮的快速上涨。
各省份工业部门资源配置效率与住房价格的关系见图5。 可以发现,相比于欠发达地区,发达地区整体房价偏高。例如广东2017年的商品房价格已经接近9000元/平方米,而位于欠发达地区的宁夏,2017年的商品房价格还不到3000元/平方米,大约是广东省的1/3。从时间维度来看,不管是发达地区还是欠发达地区,各省份的住房价格都呈上升趋势,而工业部门的资源配置效率则呈波动下降趋势,二者之间呈现负相关关系;并且住房价格增长越快,工业部门资源配置效率下降幅度越大。自2011年前后,各省的住房价格开始了新一轮的走高,与此同时,各省份工业部门的资源配置效率出现结构性的下滑。
接下来,本文以就业人数为权重,将30个省份工业部门的资源配置效率进行加权,得到全国平均工业部门资源配置效率,并计算出全国平均工业部门资源配置效率增长率(见表5)。可以看出,在2008年以前,全国平均工业部门资源配置效率在波动中有所上升,从0.733435增长到0.764494;自2008年之后,全国平均工业部门资源配置效率出现波动下降趋势,到2017年降至0.576769。这与上文六个省份工业部门资源配置效率的变化趋势是一致的。而全国平均部门工业资源配置效率增长率整体上呈下降趋势,甚至从2008年到2010年连续为负数。比较2004年前后的全国平均工业部门资源配置效率增长率可以发现,全国平均工业部门资源配置效率增长率在2004年出现了整体下滑,增长率一路下降为负数。而2004年之后,我国住房价格却开始快速上涨。
全国平均工业部门资源配置效率增长率和住房价格增长率之间的关系见图6。可以看出,全国平均工业部门资源配置效率增长率与住房价格增长率呈现明显的负相关关系。2004年以来,住房价格开始走高,而全国平均工业部门资源配置效率增长率却开始出现结构性下滑,特别是2009年,住房价格涨幅高达近19.91%,为2002—2017年的最高峰,而同年全国平均工业部门资源配置效率增长率也跌至2002年以来的谷底,为-9.89%。综合以上分析,本文认为,住房价格迅速上升,会导致工业部门的资源配置效率下降,下文对该假说进行验证。
五、实证结果与分析
(一)变量描述性统计
表6列示了各变量的描述性统计结果,其中工业部门资源配置效率按各年各省份工业就业人数进行加权处理。数据显示,在本文考察的2001—2017年期间,30个省份的工业部门资源配置效率在0.000775和0.08838范围内波动,不同省份间的工业资源配置效率差距较大,这说明各省工业部门资源配置效率水平并不平衡。
(二)实证结果
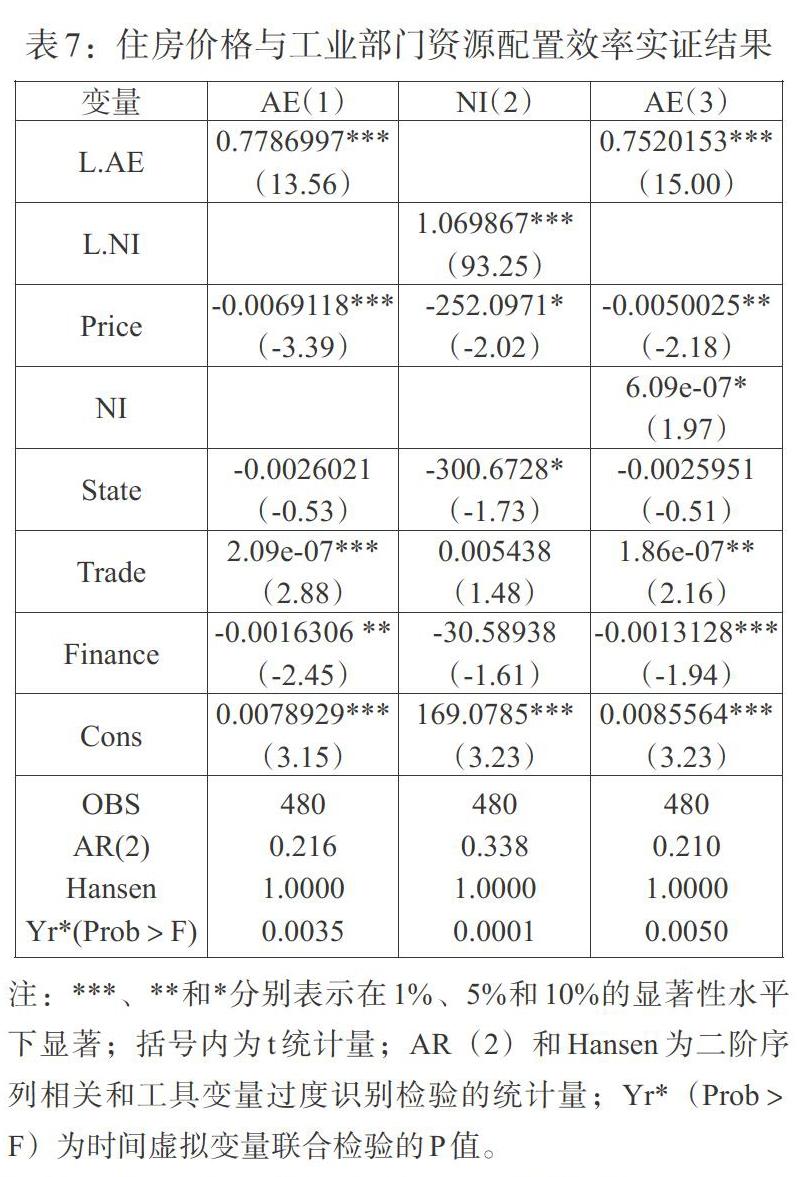
本文借鉴温忠麟和叶宝娟(2014)[40]提出的中介效应检验流程(见图4),采用系统GMM估计方法进行实证分析,共计510个样本。由于同一个省份不同时期之间的扰动项一般存在自相关,而普通标准误差计算方法假设扰动项是独立同分布的,故普通标准误差的估计并不准确,本文采用聚类稳健标准误差。
为控制宏观经济波动对配置效率的影响,模型中加入2001—2017年的时间虚拟变量yr*,为防止产生共线性,剔除掉第一年的时间虚拟变量yr1。yr*的联合检验P值表明,三个方程均通过了时间虚拟变量的联合显著性检验。此外,使用系统GMM估计方法有一个前提,即扰动项[εit]不存在自相关,而AR(2)统计量可对此条件进行检验。表7中三个方程的AR(2)统计量对应的P值分别为0.216、0.338、0.210,均表明扰动项不存在二阶自相关,因此使用系统GMM估计方法的前提条件成立。本文还采用Hansen检验对模型使用的工具变量进行过度识别检验,表7中Hansen统计量对应的P值均为1.0000,表明无法拒绝“所有工具变量均有效”的原假设。以上检验结果说明了模型设定的合理性和工具变量的有效性。
表7中结果(1)—(3)分别为式(11)—(13)的回归结果。可以看出,工業部门资源配置效率的当期表现受到其滞后项表现的正向影响,在直接效应中估计系数为0.7786997,而在间接效应中系数为0.7520153,均在1%显著性水平下显著,这意味着工业部门资源配置效率较高的省份有进一步提升配置效率的趋势。结果(1)和结果(3)中住房价格对工业部门资源配置效率的系数[c]和[c]均显著为负,说明住房价格快速上涨会导致工业部门的资源配置效率下降。同时,在加入资本投资这一中介变量后,该系数由-0.0069118提高至-0.0050025,而中介变量(NI)的系数b显著为正,说明在住房价格对工业部门资源配置效率的负向影响中,资本投资起到了显著的中介效应;结果(2)中地区住房价格(Price)的估计值a在10%水平下为负,表明地区住房价格的上升会吸引部分资金,导致工业部门新增固定资产投资不足。根据中介效应检验流程,由于系数a和b均显著,故无须进行bootstrap检验,报告资本投资的部分中介效应量约为[abc]= 3.1%,即住房价格通过资本投资这一中介变量对工业部门资源配置效率影响的大小为3.1%。上述结果均验证了本文的理论分析假设。
就控制变量而言,进出口总额(Trade)对资源配置效率产生正向影响,并且在5%水平下显著,这意味着贸易发展水平越高的省份,其工业部门的资源配置效率就越高;财政激励与工业部门资源配置效率高度负相关,表明政府干预加剧了资源错配,从而降低配置效率;国有企业比重对配置效率产生负向影响,与理论预期一致,但不显著。
(三)稳健性检验
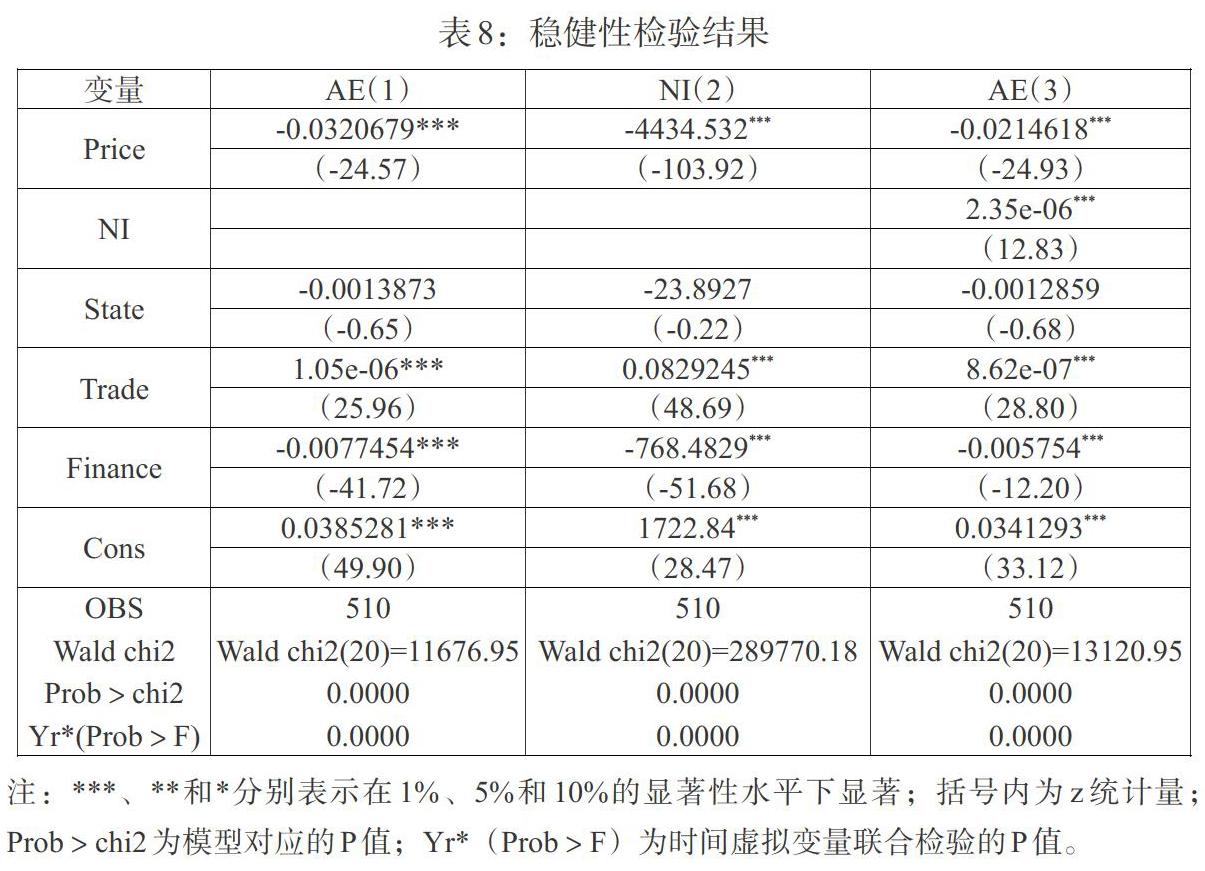
为了保证估计结果的可靠性,本文对系统GMM估计结果做进一步的稳健性检验。鉴于省份间省情不同,截面跨度较大,宏观经济的波动也会从整体上影响各省份的工业资源配置效率,因此不同省份干扰项的不同波动表现为截面异方差,且同一时点上不同省份间干扰项又存在一定的相关性。统计检验结果支持了这一想法,故采用附加权重矩阵的广义最小二乘法(GLS)估计多方程模型,同样在模型中加入控制宏观经济波动的时间虚拟变量yr*,结果见表8。
对比表7和表8可以发现,估计结果的系数符号及显著性基本一致。因此,本文的主要实证结论是可信的。
六、研究结论与对策建议
本文首先使用DEA窗口分析法测算出工业部门资源配置效率;然后,為克服内生性问题,采用系统GMM估计方法,在中介效应模型框架下利用省级动态面板数据对住房价格、资本投资和工业部门资源配置效率的关系进行了实证分析;最后,利用GLS估计方法对估计结果进行稳健性检验。结果表明,住房价格对工业部门资源配置效率产生显著的负向冲击,且资本投资在其中发挥了显著的部分中介作用,中介效应量为3.1%。随着住房价格的不断上涨,房地产业会吸纳更多资金而导致工业部门资本投资下降,从而对资源配置效率产生负面影响,资源配置效率的下降又会阻碍全要素生产率的提升,进而削弱经济持续增长的动力。
基于本文结论,在我国经济转型升级与持续推进供给侧结构性改革的背景下,相关部门需要重视房地产市场发展与工业部门资本投资之间的平衡:第一,应进一步优化资本结构,推动房地产市场的良性发展要根据各地区实际情况合理控制住房资本总量,防止房地产投资增长过快。同时,进一步深化供给侧结构性改革,拓宽民间投资渠道,防止民间资本过度流向房地产行业。第二,以合理测度住房基础价值为前提,构建科学的房地产市场长效调控机制。要积极开展相关调查统计工作,完善数据库建设,强化对相关理论探索与政策研究的管理优化与经费支持。第三,有效结合市场手段和非市场手段,推进基础制度建设。一方面,以市场配置资源为基础性制度安排,提高工业部门资源配置效率及全要素生产率,促进经济高质量发展。另一方面,通过适度调节来解决房地产市场外部性与市场失灵,以更好地应对经济增长过程中出现的结构失衡等问题,在提高效率的同时兼顾公平,保障我国经济持续健康发展。
参考文献:
[1]陈永伟,胡伟民.价格扭曲、要素错配和效率损失:理论和应用 [J].经济学(季刊),2011,(4).
[2]Hsieh C T,B J Klenow. 2009. Misallocation and Manufacturing TFP in China and India [J].The Quarterly Journal of Economics,2009,(4).
[3]丁志国,赵宣凯,苏治.中国经济增长的核心动力——基于资源配置效率的产业升级方向与路径选择 [J].中国工业经济,2012,(9).
[4]邵宜航,步晓宁,张天华.资源配置扭曲与中国工业全要素生产率——基于工业企业数据库再测算 [J].中国工业经济,2013,(13).
[5]张建华,邹凤明.资源错配对经济增长的影响及其机制研究进展 [J].经济学动态,2015,(1).
[6]Restuccia D,R Rogerson. 2008. Policy Distortions and Aggregate Productivity with Heterogeneous Establishment [J].Review of Economic Dynamics,(4).
[7]Brandt L,T Tombe and X Zhu. 2013. Factor Market Distortions Across Time, Space and Sectors in China [J].Review of Economic Dynamics,(1).
[8]张佩,马弘.借贷约束与资源错配——来自中国的经验证据 [J].清华大学学报(自然科学版),2012,(9).
[9]张庆君.要素市场扭曲、跨企业资源错配与中国工业企业生产率 [J].产业经济研究,2015,(4).
[10]Midrigan V,D Y Xu. 2014. Finance and Misallocation:Evidence from Plant-level Data [J].American Economic Review,(2).
[11]孙浦阳,蒋为,张龑. 产品替代性与生产率分布——基于中国制造业企业数据的实证 [J].经济研究,2013,(4).
[12]杨光,孙浦阳,龚刚. 经济波动、成本约束与资源配置 [J].经济研究,2015,(2).
[13]周黎安,赵鹰妍,李力雄.资源错配与政治周期[J].金融研究,2013,(3).
[14]韩剑,郑秋玲.政府干预如何导致地区资源错配——基于行业内和行业间错配的分解 [J].中国工业经济,2014,(11).
[15]靳来群,林金忠,丁诗诗. 行政垄断对所有制差异所致资源错配的影响 [J].中国工业经济,2015,(4).
[16]陈艳利,乔菲,孙鹤元.资源配置效率视角下企业集团内部交易的经济后果 [J].会计研究,2014,(10).
[17]梁云芳,高鐵梅,贺书平.房地产市场与国民经济协调发展的实证分析 [J].中国社会科学,2006,(3).
[18]冯玉梅,杨瑞桐. 房地产业金融资源配置、比较优势与经济增长 [J].山东社会科学,2018,(11).
[19]Han,L,M Lu. 2017. Housing Prices and Investment:An Assessment of China's Inland-favoring Land Supply Policies [J].Journal of the Asia Pacific Economy,(22).
[20]陈斌开,金箫,欧阳涤非.住房价格、资源错配与中国工业企业生产率 [J].世界经济,2015,(4).
[21]张巍,许家云,杨竺松.房价、工资与资源配置效率——基于微观家庭数据的实证分析 [J].金融研究,2018,(8).
[22]罗双成,陈卫民.房价上涨、要素错配与中国创新型城市发展 [J].上海经济研究,2019,(3).
[23]罗知,张川川.信贷扩张、房地产投资与制造业部门的资源配置效率 [J].金融研究,2015,(7).
[24]余泳泽,李启航. 城市房价与全要素生产率:“挤出效应”与“筛选效应”[J].财贸经济,2019,(1).
[25]徐妍,郭品. 房价、资源错配与企业创新——基于房价效率因素和非效率因素的分析 [J].经济问题,2019,(7).
[26]Farrell M J. 1957. The Measurement of Productive Efficiency [J].Journal of the Royal Statistical Society, (120).
[27]吕江林.我国城市住房市场泡沫水平的度量 [J].经济研究,2010,(6).
[28]谢攀,林致远.地方保护、要素价格扭曲与资源误置——来自A 股上市公司的经验证据 [J].财贸经济,2016,(2).
[29]林嵩.房地产行业对于创业活动的挤出效应——基于中国跨地区面板数据的分析 [J].经济管理,2012,(6).
[30]张杰,杨连星,新夫.房地产阻碍了中国创新么?——基于金融体系贷款期限结构的解释 [J].管理世界,2016,(5).
[31]王文春,荣昭.房价上涨对工业企业创新的抑制影响研究 [J].经济学(季刊),2014,(2).
[32]杨大强,张爱武.1996—2005年中国商业银行的效率评价——基于成本效率和利润效率的实证分析 [J].金融研究,2007,(12).
[33]盛鹏飞.中国能源效率偏低的解释:技术无效抑或配置无效 [J].产业经济研究,2015,(1).
[34]Charnes A,W Copper,B Golany et al. 1985. Foundations of Data Envelopment Analysis for Pareto-Koopmans Efficient Empirical Production Functions [J].Journal of Econometrics,(1).
[35]Sufian M. 2007. Benchmarking the Efficiency of the Korean Banking Sector:A DEA Approach [J].Benchmarking:An International Journal,(1).
[36]Baron RM,Kenny DA. 1986. The Moderator Mediator Variable Distinction in Social Psychological Research:Conceptual,Strategic,and Statistical Considerations [J].J Pers Soc Psychol,51(6).
[37]Arellano F,S Bond. 1991. Some Test of Specification for Panel Data:Monte Carlo Evidence and an Application to Employment Equations [J].Review of Economic Studies,(58).
[38]Blundell R,S Bond. 1998. Initial Conditions and Moment Restriction in Dynamic Panel Data Models [J]. Journal of Econometrics,(87).
[39]钱学锋,陈勇兵.国际分散化生产导致了集聚吗:基于中国省级动态面板数据GMM 方法 [J].世界经济,2009,(12).
[40]温忠麟,叶宝娟.有调节的中介模型检验方法:竞争还是替补 [J].心理学报,2014,(5).
Abstract:Taking the decomposition of cost frontier theory on the resource allocation efficiency,this paper measures the efficiency of the resource allocation of the industrial sectors. Based on this,capital investment is selected as the intermediary variable and panel data of 30 provinces in China from 2001 to 2017 are used,adopting the systematic GMM method,this paper empirically analyzes the influence of housing price on resource allocation efficiency of industrial sector by using stepwise regression intermediary effect analysis model. It is found that the housing price has a significant negative impact on the resource allocation efficiency of the real economy through the "blood drawing effect",in which capital investment plays a significant part of the mediating effect.
Key Words:housing prices,capital investment,resource allocation efficiency in industry sectors,the mediating effect,systematic GMM

