双齿轮式排肥器设计与试验

顿国强 于春玲 郭艳玲 纪文义 ISLAM K R 杜佳兴

(1.东北林业大学机电工程学院，哈尔滨 150040；2.东北农业大学工程学院，哈尔滨 150030；3.俄亥俄州立大学土壤、水和生物能源中心，派克顿 45661；4.黑龙江省农业科学院佳木斯分院，佳木斯 154007)

0 引言

化肥用量和施肥均匀性均严重影响着作物的产量，适量的化肥能提高农作物的产量，但过量或是不合理的施用化肥不仅达不到高产、优质的目的，还会降低化肥的利用效果，浪费资源、污染环境[1-2]。相关学者对精量施肥控制技术做了大量研究[3-7]。

排肥器是施肥机械的关键部件，目前，国内外设计和研究的排肥器形式主要有外槽轮式、转盘式、离心式、螺旋式、星轮式和振动式等[8]，其中应用最多的是外槽轮式排肥器[9]，其结构简单、操作方便、价格便宜[10-11]，但也存在化肥施用量大、排肥均匀性差等问题，只能使用流动性好的松散化肥和复合粒肥[12-13]。为了提高排肥器排肥均匀性、控制排肥量，许多学者做了大量研究。顿国强等[14]通过在外槽轮排肥器下端安装肥料调配装置，有效改善了排肥流量脉动的现象；丁筱玲等[15]分别以排肥器槽深及施肥速度作为优先控制策略分析了对排肥稳定性的影响，并改进了导流槽的结构；祝清震等[16-17]分析了槽轮半径、凹槽数目、有效工作长度以及凹槽截面形状对直槽轮式排肥器排肥性能的影响。这些研究成果为施肥装置的进一步优化提供了参考。

为了提高颗粒肥料施肥均匀性，本文设计一种双齿轮式排肥器，分析结构参数对排肥效果的影响，建立排肥过程数学模型，运用离散元法仿真分析不同结构参数对排肥均匀性的影响，优化结构参数，并应用3D打印技术制造最优结构参数组合下的双齿轮式排肥器，与外槽轮排肥器进行对比验证试验，以期为排肥器的进一步优化提供参考。

1 工作原理与结构设计

1.1 结构组成

双齿轮式排肥器的结构主要包括排肥盒、左右渐开线排肥齿轮、左右传动齿轮、排肥口等，如图1所示。其中渐开线排肥齿轮是完成排肥作业的关键部件。

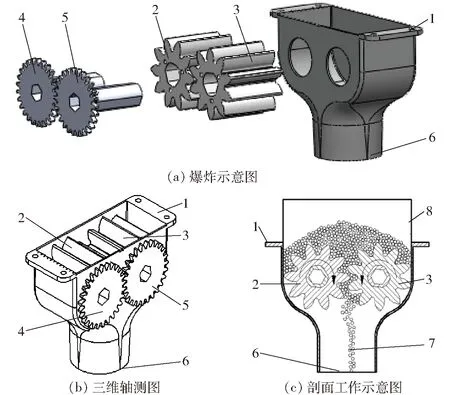
图1 双齿轮式排肥器结构示意图

1.2 工作原理

工作前，左右传动齿轮分别固装在左右渐开线排肥齿轮上，动力输入轴固装在左传动齿轮上。工作时，动力输入轴顺时针转动，带动左传动齿轮与右传动齿轮啮合转动，进而带动固装在其上的左右渐开线排肥齿轮转动，左右渐开线排肥齿轮是由啮合状态水平保持一段距离得到的相对位置不变的间隙排肥齿轮，排肥齿轮转动过程中带动肥箱内的肥料转动，肥料随着齿脊与齿槽间形成的容肥空间向下运动，落入排肥口，由于双齿轮的齿脊与齿槽连续交替作业，排肥齿轮的容肥空间大小基本不变，无脉动现象，肥料颗粒连续稳定地排出，提高了排肥流量的均匀性，本排肥器通过调节排肥轮的转速控制排肥量。

1.3 双渐开线排肥齿轮设计

双渐开线排肥齿轮是排肥过程中的关键部件，齿脊与齿槽间形成的容肥空间大小决定了排肥量，因此，为了得到影响排肥量的具体结构参数，需对双齿轮的容肥空间进行计算。

排肥器排出肥料的总质量为

m1=ρV

(1)

式中m1——排出肥料质量，g

ρ——肥料密度，g/cm3

V——排出肥料体积，cm3

双渐开线排肥齿轮由两个处于啮合状态的齿轮水平分开长度c得到的相对位置不变的非啮合齿轮，即排肥齿轮，啮合状态如图2所示，排肥状态如图3所示，阴影部分为两齿轮重合区域。图中参数分别为齿轮分度圆半径r，啮合状态齿轮中心距a1，左、右排肥齿轮转速n1、n2，排肥齿轮齿顶圆半径ra，排肥齿轮中心距a2。

图2 渐开线齿轮啮合状态

图3 渐开线齿轮排肥状态

由齿轮啮合基本条件可知

a1=2r

(2)

c=a2-a1

(3)

n1=n2

(4)

排肥器排出肥料总体积为

(5)

其中

k=2z

(6)

式中S1——两渐开线齿轮容肥区的面积，mm2

b——排肥齿轮长度，mm

k——排肥齿轮转动一周齿脊、齿槽重合次数

n——排肥齿轮转速，r/min

t——排肥器运动时间，s

z——排肥齿轮齿数

排肥齿轮转速n与n1、n2大小相等，当渐开线齿轮齿脊、齿槽运动到如图3所示状态时，计算一次重合次数，排肥轮转动一周重合次数为两排肥轮总齿数。

采用分度圆法[18]计算单个渐开线齿轮截面面积为

Sr=πr2

(7)

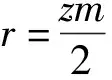
(8)

式中Sr——单个排肥齿轮齿脊截面面积，mm2

m——排肥齿轮模数，mm

单个渐开线齿轮齿槽的面积为

Sk=Sa-Sr

(9)

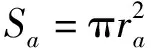
(10)

(11)

则单个齿槽的面积为

(12)

式中Sk——单个排肥齿轮的总齿槽面积，mm2

Sa——单个排肥齿轮的齿顶圆面积，mm2

Sc——单个齿槽面积，mm2

两渐开线齿轮齿脊、齿槽重合情况如图4所示，其中阴影部分为两齿轮齿槽间隙即容肥区，为方便计算将齿顶圆与轮齿的重合区域近似看作等腰梯形，则重合区域的面积为

St=lh

(13)

其中

h=2ra-a2

(14)

联立式(3)、(14)可得

(15)

式中St——重合区面积，mm2

l——等腰梯形中线长度，mm

h——等腰梯形高度，mm

图4 排肥齿轮容肥区示意图

由图4可知，重合区域梯形的中线可通过渐开线齿轮任意圆的齿厚得到，即

(16)

(17)

(18)

式中Si——中线所在圆齿厚，mm

s——渐开线齿轮分度圆齿厚，mm

ri——中线所在圆半径，mm

α——渐开线齿轮压力角，(°)

αi——中线所在圆压力角，(°)

由渐开线齿轮极坐标方程式可知

(19)

式中αk——渐开线在任意点K的压力角，(°)

rk——渐开线在任意点K的向径，mm

rb——渐开线齿轮基圆直径，mm

由渐开线齿轮极坐标方程式可得

(20)

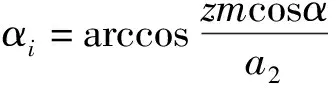
(21)

(22)

两排肥齿轮容肥空间可表示为单个齿槽面积与等腰梯形面积的差

S1=Sc-St

(23)

即

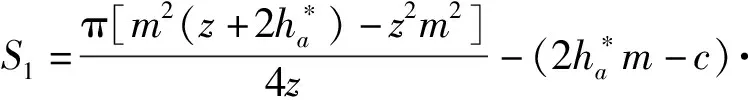
(24)

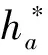
以标准垄垄距65 cm、作业速度上限3 m/s为设计依据，由式(1)、(5)、(24)计算可知，当排肥轮工作转速为60 r/min时，其理论排肥量可达到极限施肥量750 kg/hm2的农艺要求。本文首先以排肥轮压力角及排肥轮间隙为试验因素，以改善排肥流量均匀性为优化准则，通过仿真试验优化排肥轮结构，设置仿真试验排肥轮转速为60 r/min，其次通过台架试验的方式验证通过调整排肥轮转速可控制排肥量。

2 离散元仿真平台建立

施肥作业过程中，肥料颗粒处于流动的状态，利用传统的试验研究方法，无法捕捉施肥过程中肥料颗粒所处的力学状态及空间位置分布[20-21]。采用离散元软件EDEM进行仿真研究及分析，可有效模拟排肥器的实际作业过程，评价其作业性能，加快排肥器的研发进度[22-23]。LIEDEKERKE等[24-25]通过离散元法分析了离心撒肥部件参数变化对肥料颗粒土壤分布状况的影响；LANDRY等[26]运用离散元模型仿真分析了离心撒肥机对土壤的适应状况；顿国强等[27]采用EDEM离散元软件，分析了外槽轮排肥器排肥舌倒角机构参数对排肥均匀性的影响；杨洲等[28-29]利用EDEM仿真软件和3D打印成型技术分析了外槽轮式排肥器结构参数和工作参数对排肥量的影响。

排肥齿轮是排肥过程中的关键部件，其结构参数的变化直接影响排肥量及其均匀性，因此，采用EDEM建立双齿轮排肥器的仿真模型，分析各结构参数变化对排肥量及其均匀性的影响，得到双齿轮的最佳结构参数。

2.1 肥料颗粒离散元模型

选用江苏晋煤恒盛化工股份有限公司生产的尿素作为离散元建模的试验材料，其粒度范围为1.73～3.74 mm。随机选取300粒尿素颗粒，测量尿素颗粒的三维尺寸(长L、宽B、高H)，测量结果如表1所示。

表1 颗粒参数

计算肥料颗粒的等效直径和球度

(25)

(26)

式中D——肥料颗粒的等效直径，mm

Sp——肥料颗粒的球度，%

结果分别为2.51 mm和93.66%，颗粒球度Sp大于90%，因此选用直径为2.51 mm的球体颗粒作为仿真的颗粒模型，半径标准差为0.199 mm，服从正态分布。

2.2 仿真参数设置

肥料颗粒表面无黏附作用，因此选择EDEM软件中默认的接触模型Hertz-Mindlin(no slip)[30]，作为肥料颗粒与肥料颗粒、肥料颗粒与排肥装置之间的接触模型，其在力的计算方面精确且高效[31-32]。肥料颗粒、排肥装置的材料参数与接触参数设置如表2所示。

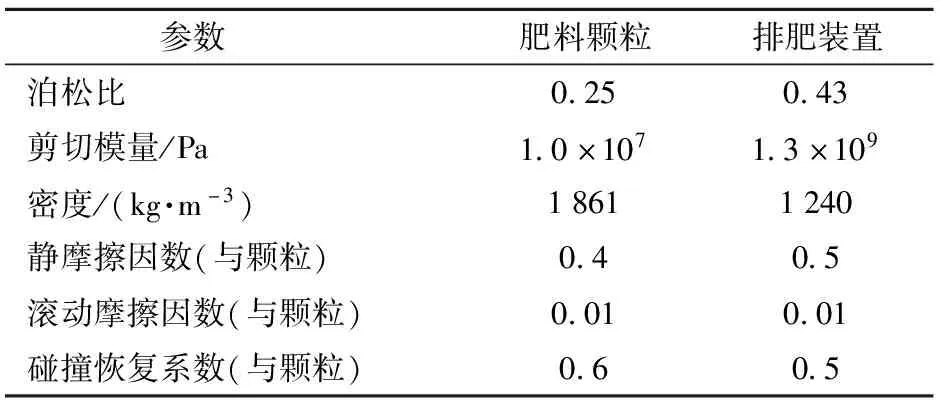
表2 离散元仿真参数设置

2.3 排肥器离散元模型

简化双齿轮式排肥器模型，导入EDEM中，按照表2设置参数。在肥箱上部建立颗粒工厂，生成的肥料颗粒半径呈正态分布，标准差为0.199 mm，颗粒生成速度为10 000个/s，生成总量为20 000个，产生颗粒总时间为2 s，设置排肥轮第2秒开始转动，排肥轮转速为60 r/min，在肥料收集盒底部设置肥料质量监测区。仿真步长为2.0×10-5s，数据记录间隔为0.005 s，仿真总时间为10 s，仿真过程如图5所示。

图5 渐开线排肥齿轮EDEM仿真模型

2.4 排肥性能评价方法

本文主要研究排肥齿轮结构参数对排肥量均匀性的影响，为了准确评价在EDEM仿真试验过程中不同结构参数对排肥性能的影响，参考JB/T 9783—2013《播种机外槽轮排肥器》可知排肥均匀度变异系数可反映排肥量的均匀性和排肥过程中的稳定性，因此以排肥均匀度变异系数作为双齿轮式排肥器排肥性能的评价指标，若变异系数过大，则排肥器的排肥稳定性和均匀性都较差，反之数值越小，排肥效果越好。

仿真结束后，统计各个时刻肥料质量监测区内肥料颗粒的总质量，计算仿真过程中肥料颗粒质量的均值

(27)

式中φ——检测的总次数

ki——第i时刻监测区内肥料颗粒的质量，g

计算仿真过程中质量监测区域内肥料颗粒质量的标准差

(28)

得到仿真过程排肥器排肥均匀度变异系数

(29)

3 单因素试验与结果分析

3.1 排肥轮压力角与排肥均匀性的关系

排肥轮为渐开线齿轮，其压力角的大小会改变容肥空间的大小与形状，进而影响排肥过程中肥料下落的均布效果。依据渐开线齿轮设计原理，试验选取压力角分别为10°、15°、20°、25°、30°、35°、40°的7组排肥轮，进行排肥过程中排肥流量均匀性的对比单因素试验，其中7组排肥轮间隙统一取5 mm。

不同压力角的排肥轮排肥均匀度变异系数变化趋势如图6所示，随着排肥轮压力角逐渐增大，排肥均匀度变异系数先减小后增大，当排肥轮压力角为20°时，排肥均匀度变异系数最小，说明此排肥轮压力角在20°左右时，肥料分布均匀，排肥效果较好。

图6 排肥轮压力角与排肥均匀度变异系数关系

3.2 排肥轮间隙与排肥均匀性的关系

由理论分析可知，排肥轮间隙直接影响容肥空间的大小，进而影响排肥效果。已知试验肥料为尿素，直径为2.51 mm，根据前期所做预试验，排肥间隙过大，则肥料直接下落，无排肥效果，排肥间隙过小则肥料堵塞排肥轮肥料无法排出，排肥间隙分别取3、4、5、6、7 mm的5组排肥轮，进行排肥过程中排肥流量均匀性的对比单因素试验，其中5组排肥轮压力角统一为20°。

不同间隙的排肥轮排肥均匀度变异系数变化趋势如图7所示，随着排肥轮间隙逐渐增大，排肥均匀度变异系数先减小后增大，当排肥轮间隙为5 mm时，排肥均匀度变异系数最小，说明此排肥轮间隙在5 mm左右时，肥料分布均匀，排肥效果较好。

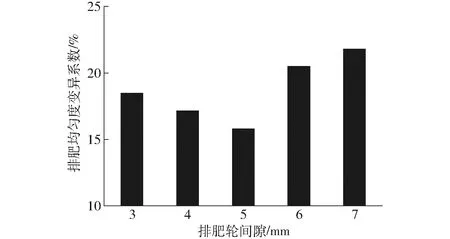
图7 排肥轮间隙与排肥均匀度变异系数关系

4 响应面试验

4.1 试验设计

通过分析排肥轮不同压力角和间隙对渐开线齿轮排肥效果的影响，对排肥轮的结构参数进行优化。选用二次通用旋转组合试验方法，分析排肥轮压力角、排肥轮间隙对肥料均匀性效果的影响，以排肥均匀度变异系数作为评价指标，在单因素仿真试验结果的基础上，选取排肥轮压力角区间为15°～ 25°，排肥轮间隙区间为4～6 mm，试验因素编码如表3所示。

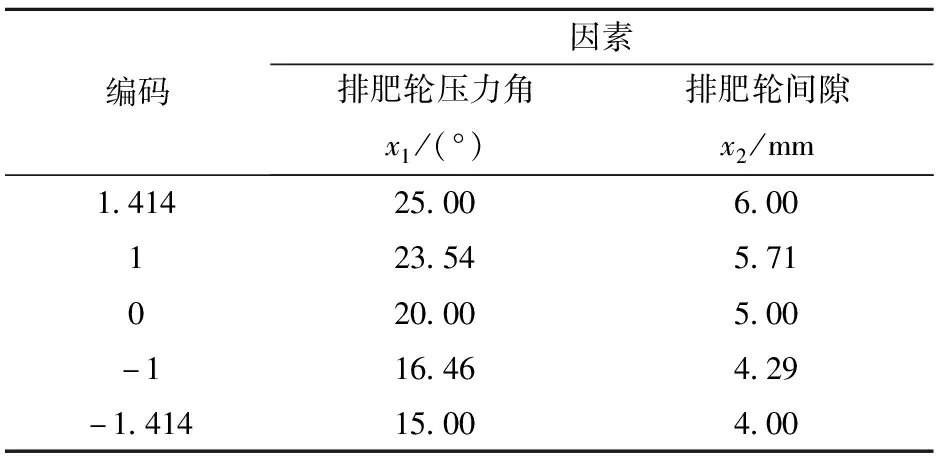
表3 试验因素编码

4.2 试验方案与结果分析

应用Design-Expert软件对试验结果进行回归分析，以确定两个试验因素下排肥均匀度变异系数的变化规律，试验方案及结果如表4所示。

以排肥轮压力角x1、排肥轮间隙x2为试验因素，以排肥均匀度变异系数σ为试验指标，运用Design-Expert软件对试验结果进行方差分析，如表5所示。

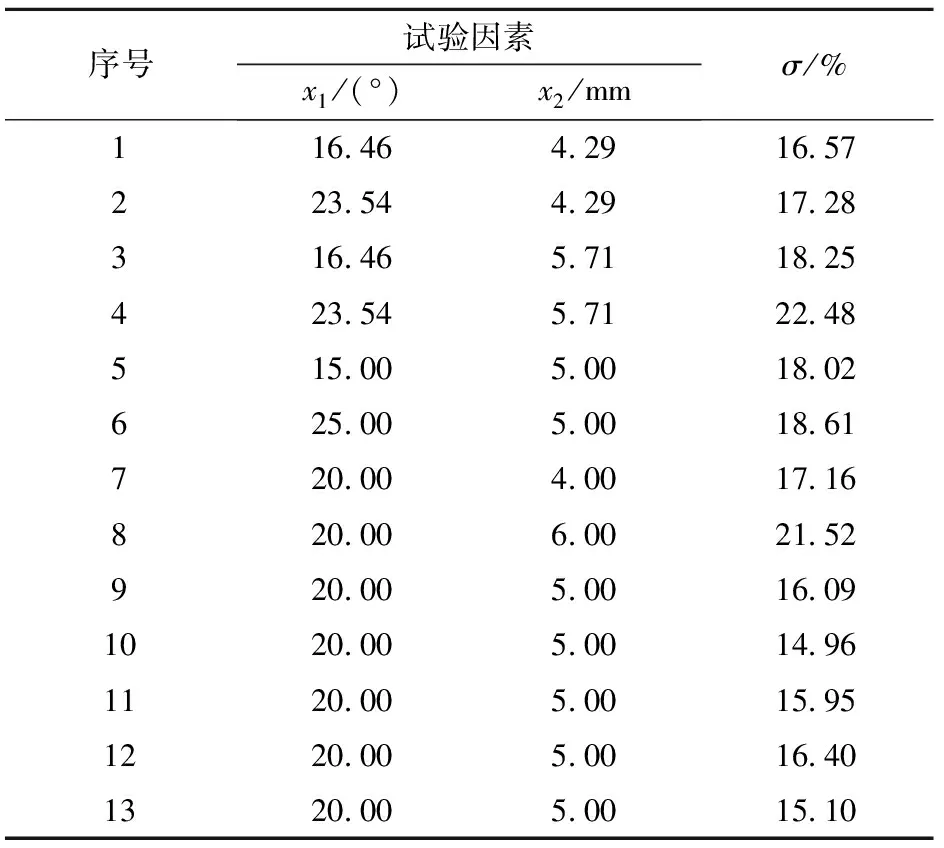
表4 试验方案与结果

表5 方差分析

注：** 表示差异极显著(P<0.01)，*表示差异显著(P<0.05)。

σ=163.43-5.57x1-39.91x2+0.35x1x2+

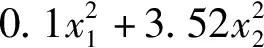
(30)

4.3 试验因素对指标的影响

排肥轮压力角及排肥轮间隙对排肥均匀度影响如图8所示。由图8a可知，变异系数σ随排肥轮压力角、排肥轮间隙的增大均呈现先增大后减小的趋势；由图8b可知，排肥轮间隙对排肥均匀度变异系数的影响比排肥轮压力角大，与表5中的方差分析结果吻合。

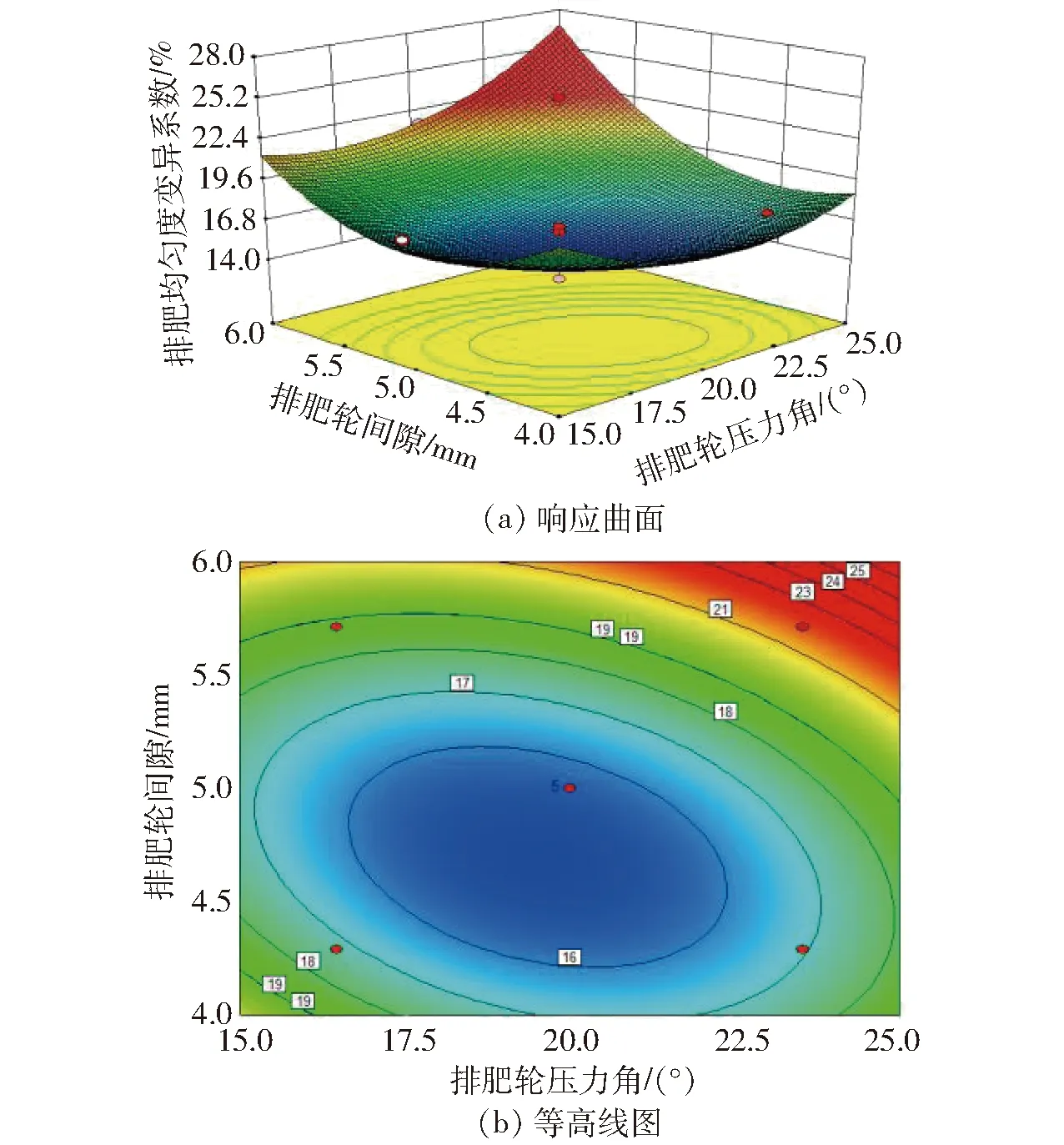
图8 试验因素对变异系数的影响

4.4 参数优化及仿真验证

为了得到排肥轮的最优结构参数，对排肥轮压力角及间隙进行参数优化，设定变异系数最大为16%，得最优参数分别为：排肥轮压力角19.52°、排肥轮间隙4.7 mm，此时排肥均匀度变异系数的理论值为15.30%。

为了检验参数优化的结果，在上述优化组合条件下进行仿真验证试验，仿真排肥均匀度变异系数为14.58%，与优化理论值偏差为0.72个百分点，仿真验证结果与理论计算结果基本一致，证明回归模型具有准确性和可行性。

5 台架验证试验

在理论分析及仿真分析后，为验证双齿轮式排肥器优化结果的可靠性与可行性，参考NY/T 1003—2006《施肥机械质量评价技术规范》对双齿轮式排肥器进行试验验证。

5.1 试验材料与仪器

试验地点为东北林业大学智能农机装备实验室，时间为2019年5月。选用江苏晋煤恒盛化工股份有限公司生产的尿素作为试验材料，其粒度范围为1.73～3.74 mm，选取最优结构参数的排肥轮，排肥轮齿数z=10，排肥轮直径d=60 mm，排肥轮槽长为30 mm，应用3D打印加工排肥齿轮及排肥器的其他结构部件，如图9所示，试验台架为自主设计的排肥试验台，台架试验如图10所示。

图9 双齿轮式排肥器实物图

图10 台架验证试验

5.2 试验方案与结果

5.2.1性能试验

本文所设计排肥器无调肥隔板，但可通过控制转速进而控制排肥量，采用单因素试验的方法，试验因素为排肥轮转速取20、30、40、50、60 r/min共5个水平，试验指标为排肥量，每个水平试验时间为10 s，试验过程中每隔2 s采集一次数据，每组试验重复5次取平均值。试验结果如表6所示，排肥量随工作时间的变化曲线如图11所示，调节排肥轮的转速可明显改变排肥量，且排肥量随工作时间呈线性变化趋势。

表6 控制转速调节排肥量试验结果

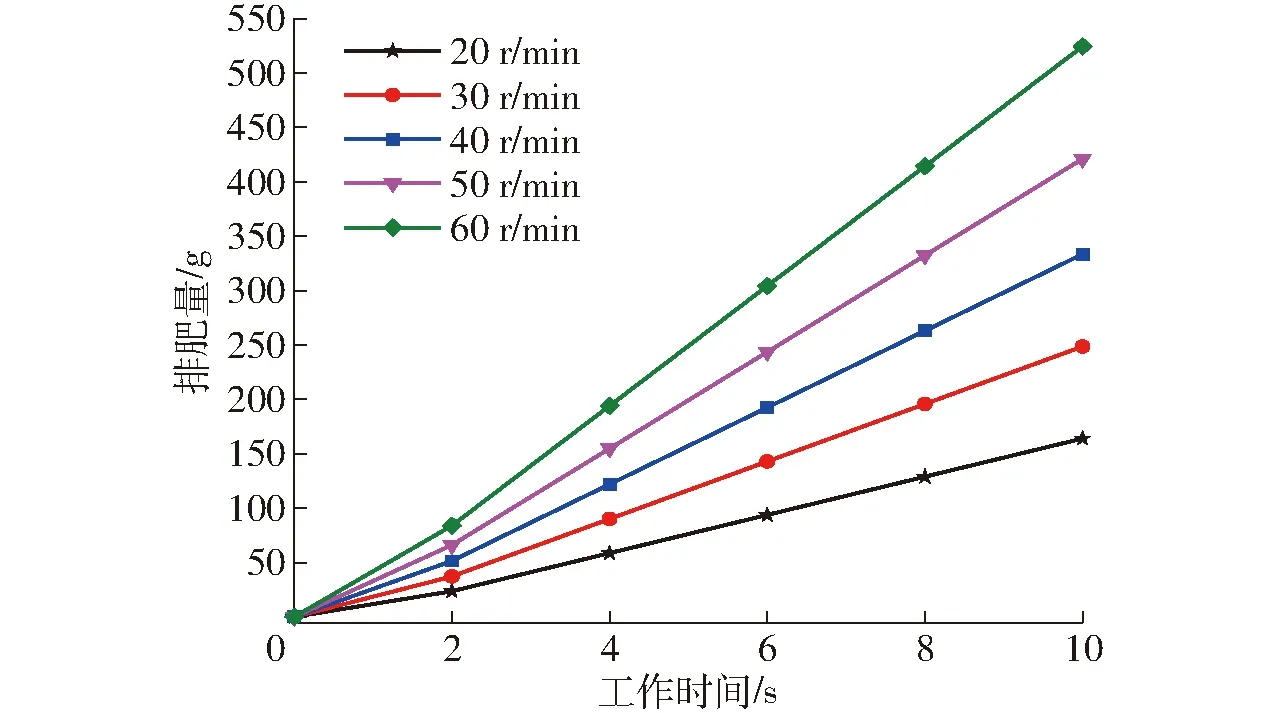
图11 不同排肥轮转速的排肥量曲线

应用Origin Pro对试验结果进行线性拟合，拟合图如图12所示，排肥流量随排肥轮转速的增加而增加，拟合曲线结果显示排肥流量与排肥轮转速呈线性相关，拟合曲线方程为：y=0.93x-1.46，R2=0.998。因此，排肥器可通过改变排肥轮转速线性调节排肥流量。

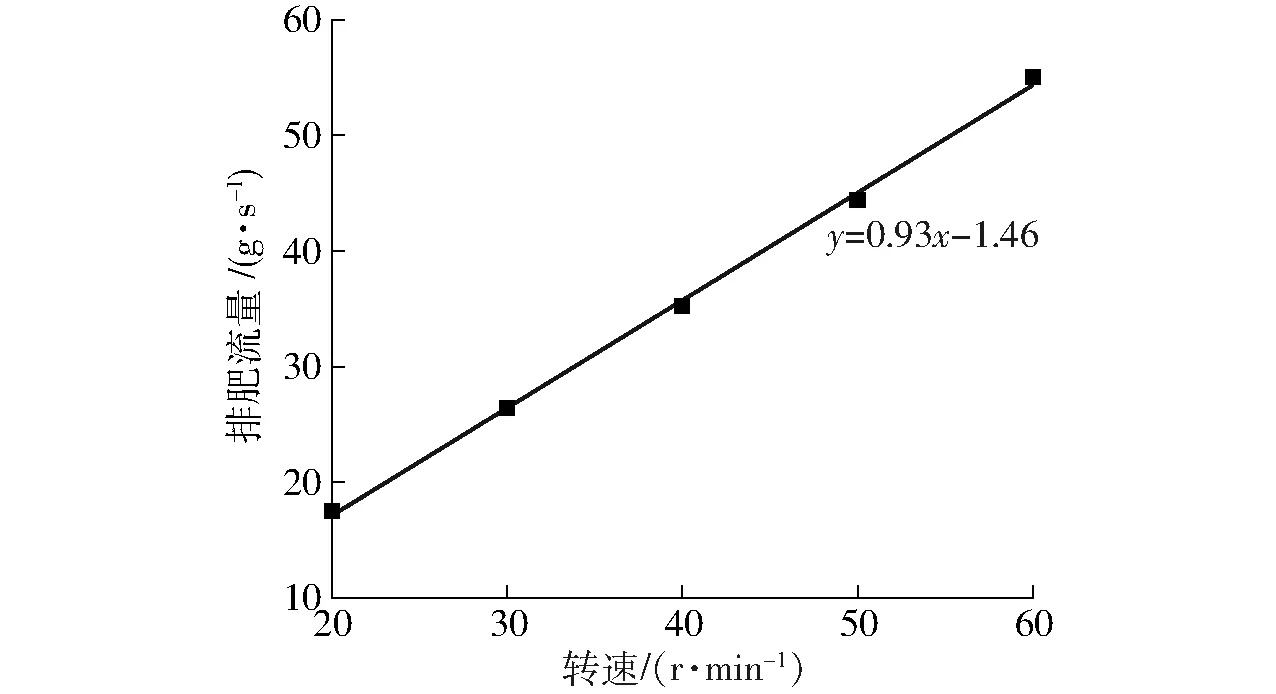
图12 排肥轮转速与排肥流量拟合曲线

5.2.2对比验证试验

为验证排肥器施肥均匀性改善的效果及仿真优化结果的准确性，将双齿轮式排肥器和市面上应用最多的外槽轮排肥器进行施肥均匀性对比验证试验，设定两者工作转速为60 r/min，工作槽长为30 mm，试验时间为10 s，每组试验重复5次取平均值，统计试验排肥量与试验均匀性变异系数，结果如表7所示。

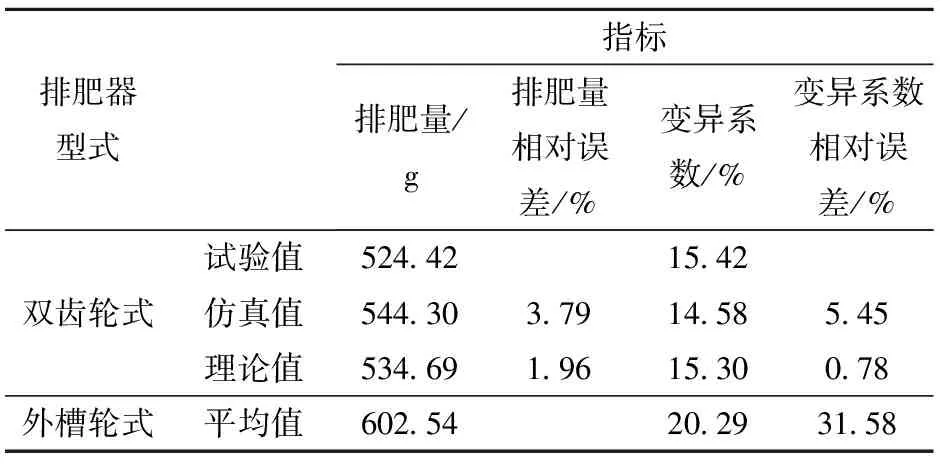
表7 对比验证试验结果

由表7可知，采用优化结构参数后的排肥轮，试验排肥量与仿真排肥量相对误差为3.79%，与理论排肥量相对误差为1.96%，通过分析确定主要原因为台架试验中肥料存在较大结块，未完全破碎，导致排肥量偏小，但相对误差均在5%以内，为可接受范围，满足实际要求。

试验变异系数与仿真值相对误差为5.45%，与理论值相对误差为0.78%，通过分析，确定出现偏差的原因主要为仿真时将颗粒理想为球状，而台架试验中所用的尿素颗粒并非标准球体，均匀性较差，且存在一定的结块现象，所以台架试验得到的变异系数与仿真值存在偏差，但偏差不大，两者基本吻合，说明仿真优化结果是准确的；同等条件下外槽轮排肥器变异系数的平均值为20.29%，优化后的排肥轮变异系数与外槽轮排肥器变异系数相对误差达31.58%，发现优化后的双齿轮式排肥器排肥效果较好，有效地提高了颗粒肥料的施肥均匀性，满足设计要求。

6 结论

(1)设计了双齿轮式排肥器，通过理论分析确定了影响其排肥均匀性的主要因素为排肥轮压力角和排肥轮间隙。

(2)单因素仿真试验结果表明，排肥轮压力角在15°～25°，排肥轮间隙在4～6 mm，排肥均匀性较好；由二次通用旋转组合试验得出最优结构参数组合为排肥轮压力角19.52°、排肥轮间隙4.7 mm，此时排肥均匀度变异系数的理论值为15.30%。

(3)台架验证试验结果表明，可通过改变排肥轮转速实现排肥量的线性调节；试验排肥量与理论排肥量及仿真排肥量基本一致，排肥均匀度变异系数试验值为15.42%，同等条件下外槽轮排肥器的变异系数为20.29%，有效地提高了颗粒肥料的施肥均匀性。