超临界二氧化碳向心涡轮泄漏特性计算与分析

赵 峰， 吕 国 川， 杨 金 广， 刘 艳， 王 晓 放

( 大连理工大学 能源与动力学院, 辽宁 大连 116024 )

0 引 言

以超临界二氧化碳(supercritical carbon dioxide，简称SCO2)为工质的布雷顿循环因具有效率高、结构紧凑以及环境友好等特点越来越受到研究者们的关注，其关键部件向心涡轮的效率对整体循环效率有显著的影响[1]，一直以来许多学者致力于SCO2向心涡轮的研究．美国桑迪亚国家实验室(Sandia National Laboratory，SNL)和贝泰船用推进公司(Bechtel Marine Propulsion Corporation，BMPC)，以及韩国能源研究所(Korea Institute of Energy Research，KIER)在SCO2循环实验中对SCO2向心涡轮进行了研究．而轮背空腔内流动状态非常复杂，其间隙泄漏损失是向心涡轮气动损失的重要组成部分[2-3]，在输出相同功率的情况下，其叶轮承受的轴向力更大，因此对间隙密封展开研究具有重要意义．

迷宫密封具有密封性好、结构简单、工作可靠等优点，适用于高温、高压、高速等场合，是一种应用极为广泛的非接触式密封．其主要机理是依靠密封间隙的节流作用和密封腔的动能耗散效应来实现密封．国内外许多研究团队对SCO2向心涡轮和迷宫密封展开了广泛而深入的研究．Yucel等[4]采用数值模拟与试验相结合的方法得到影响迷宫密封效果的主要因素，包括温度、压差、齿数和齿形等；Bariaud等[5]在涡轮转子上设计了迷宫密封结构，试验结果表明密封性能良好；朱高涛[6]采用Fluent软件对迷宫式压缩机的泄漏特性进行了详细的研究；Ma等[7]对SCO2向心涡轮轮背空腔进行气动设计，并且分别用轮背泄漏率为0.2%和2%两种算例对抽气叶片进行数值模拟，结果表明抽气叶片可以有效地减小涡轮的轴向力．

目前关于SCO2向心涡轮迷宫密封还缺乏相关研究资料．本文基于迷宫密封形式对某MW级SCO2向心涡轮轮背空腔泄漏流展开参数化研究，分析密封出口压力、密封间隙、密封齿高、密封齿数和密封齿形等对涡轮泄漏量[8]和轴向力的影响，旨在减少轮盘背部间隙泄漏损失，改善向心涡轮轮盘、涡轮轴和轴承[9]等部件的工作状况．其中，SCO2的物性参数通过NUMECA/TabGen生成的物性表格计算得到．

1 数值计算分析

1.1 几何模型

基于本课题组某MW级SCO2向心涡轮的设计结构，以轮背空腔为研究对象建立迷宫密封几何模型，如图1所示．

图1 迷宫式向心涡轮结构图

1.2 网格划分

在数值模拟过程中，湍流模型选用Spalart-Allmaras模型．经过网格无关性验证后，最终确定总网格数约为867万，其中第一层壁面网格高度ywall=0.001 mm，满足该湍流模型的要求．向心涡轮及其轮背空腔迷宫密封计算网格如图2所示．表1给出了迷宫密封的几何参数．

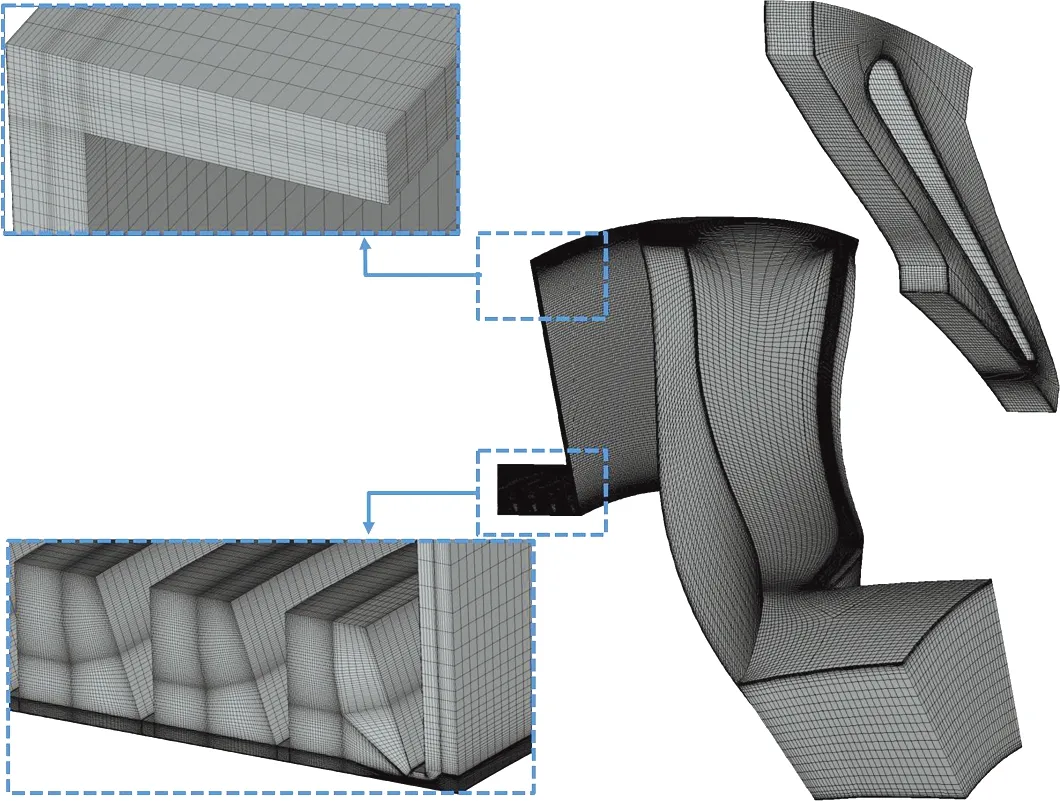
图2 轮背空腔与迷宫密封网格

表1 迷宫密封几何参数

1.3 边界条件设置

入口边界条件的设置选择给定总温、总压、气流方向以及湍流黏度，涡轮出口给定静压，密封出口压力条件给定平均静压pg，out．涡轮的工作条件如表2所示．

表2 涡轮设计点运行工况

2 模型验证

2.1 计算方法验证

为验证密封泄漏特性计算的准确性，本文基于文献[10]中的模型和试验数据，对本文中的计算方法进行验证，其中环形孔模型的具体结构尺寸如图3所示．在数值计算过程中，边界条件给定入口总温319 K，入口总压10 MPa，出口压力可根据压比(出口压力与入口压力比)进行取值．

图3 环形孔正视图(单位：mm)

由图4可知，数值计算结果整体上基本与试验数据吻合．当压比小于0.74时，数值计算结果与试验数据最为相符；当压比大于0.74时，数值计算结果与试验数据相差较大，最大相对误差发生在0.85附近，约为9%．综上，本文采用的研究方法具有一定的准确性．

2.2 迷宫密封验证

由图5、6可知，迷宫密封对涡轮轴向力F和泄漏量L影响较大．随着密封出口静压的增大，涡轮轴向力和泄漏量整体呈现减小的变化趋势，带有密封结构的涡轮轴向力与不带密封结构的涡轮轴向力，最大相差为2.727 kN，最小相差为1.658 kN．带有密封结构的涡轮泄漏量与不带密封结构的涡轮泄漏量，最大相差为0.194 kg/s，最小相差为0.032 kg/s．综上，迷宫密封能够有效改善SCO2向心涡轮泄漏流．

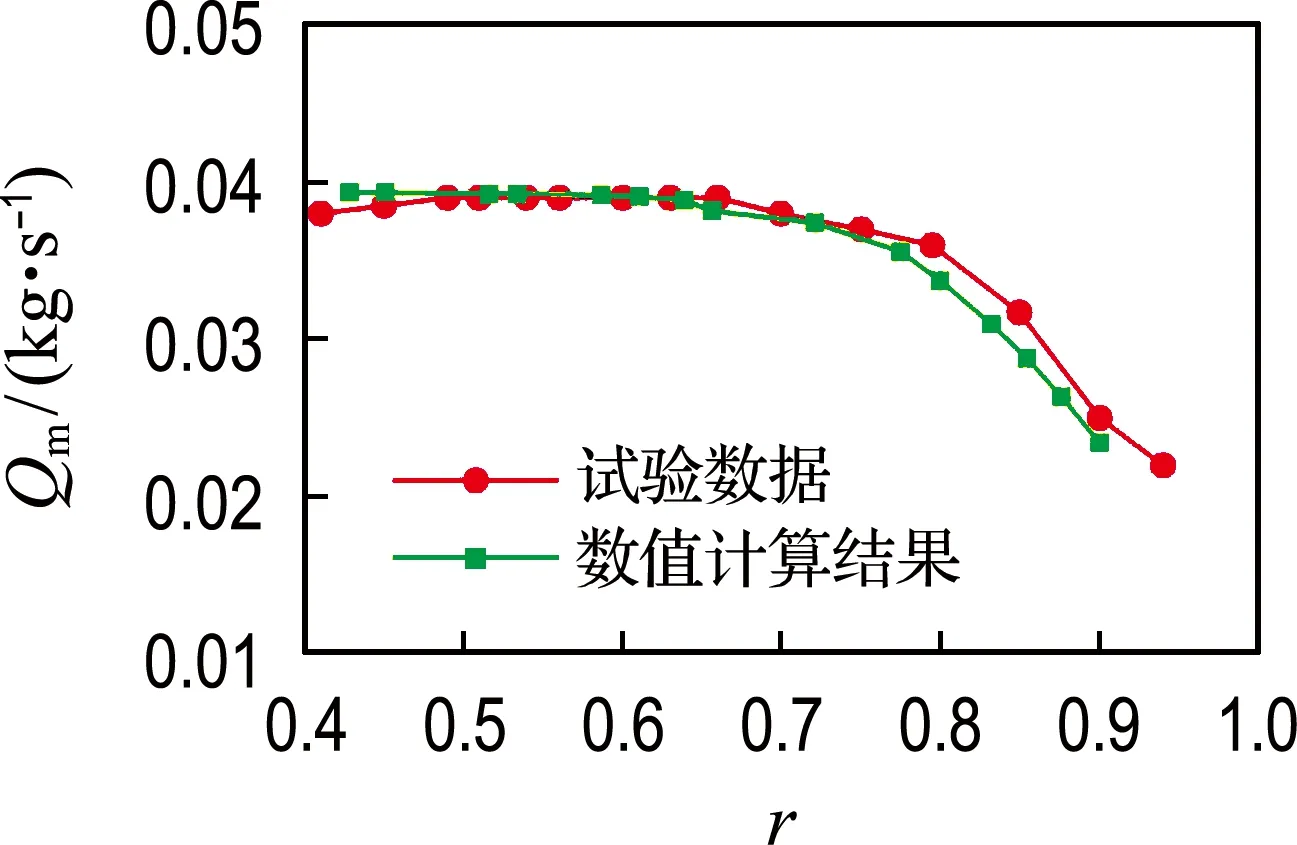
图4 SCO2环形孔试验与数值计算结果对比

图5 有无密封结构涡轮轴向力对比

图6 有无密封结构涡轮泄漏量对比

3 迷宫密封特性研究

3.1 密封出口压力对泄漏量与轴向力的影响

为研究密封出口压力对SCO2向心涡轮轮背泄漏流的影响，本文计算7种静压条件下的泄漏量和轴向力，其他条件保持不变，如图7、8所示．由图7可知随着密封出口静压的增大，泄漏量逐渐减少．密封出口静压的增大导致密封间隙中的射流减弱，密封腔内压力降低，动能耗散较多，密封性能得到改善．Li等[11]的试验研究中也有类似的结论．

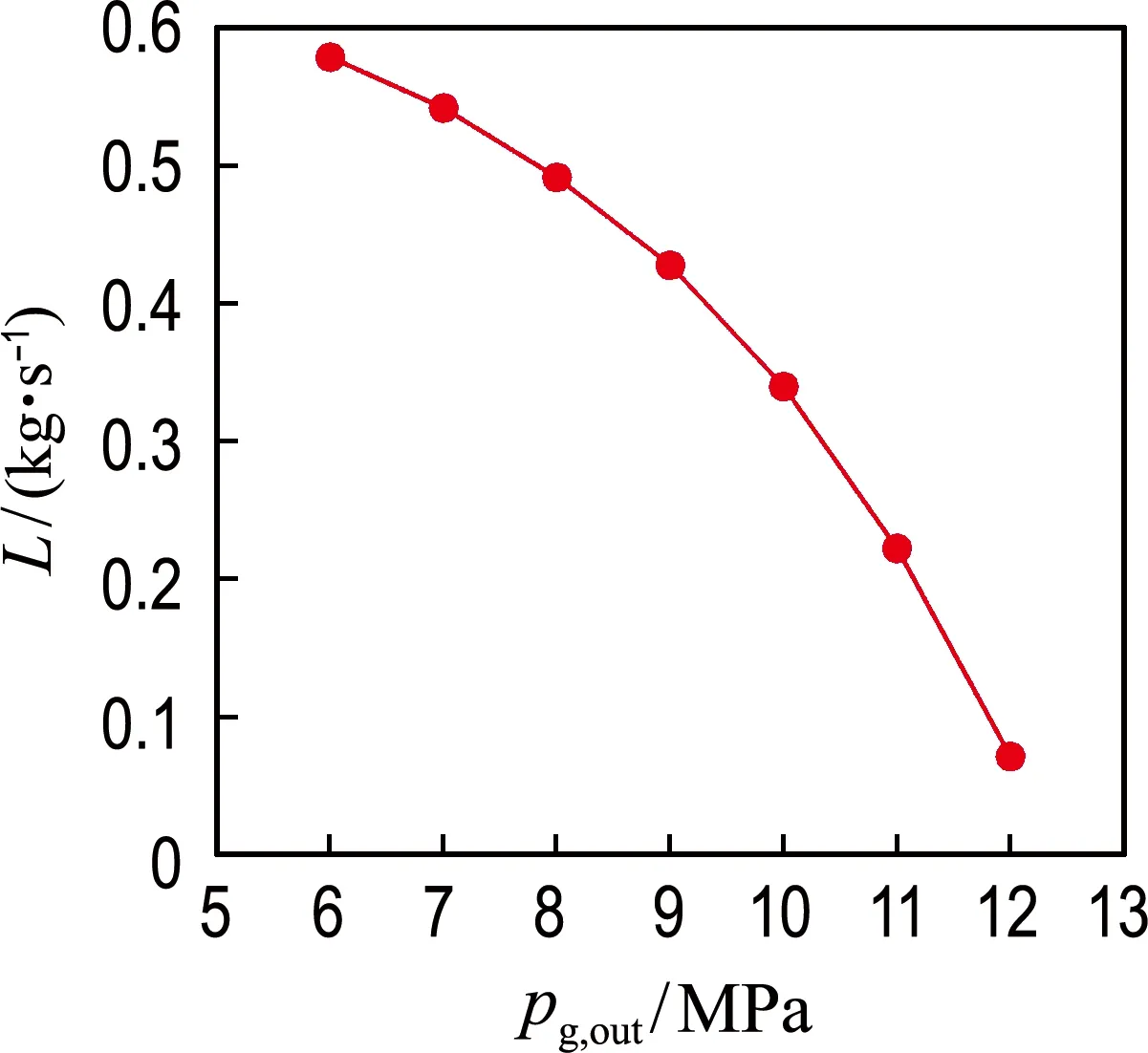
图7 泄漏量随密封出口静压的变化曲线

图8 轴向力随密封出口静压的变化曲线

与具有相同输出功率的燃气轮机相比，向心涡轮叶轮上承受的轴向力更大．作为承担轴向力的主要部件，止推轴承设计得合理与否直接影响涡轮的使用寿命，因此，轴向力计算显得十分必要．轴向力数值计算[12]主要是基于图9所示的受力分析，通过对叶轮表面和轮背空腔等处的压力分布进行积分，最终得到各部分的轴向力．图中Ft1是叶轮出口平面力，Ft2是叶片及轮毂作用力，F2是叶轮轮背作用力．假设涡轮轴向力以指向轮背方向为负方向，则涡轮轴向力合力Ft=Ft1+Ft2-F2．

将叶轮出口平面力Ft1和叶片及轮毂作用力Ft2统称为叶轮工作面轴向力F1，它指向轮背的方向定义为负方向，轮背轴向力F2为正方向．由于轴向力的最终计算结果为负值，为显示方便，图8中显示的是密封间隙s=0.20 mm时轴向力的绝对值．由图可知随着密封出口静压的增大，密封进出口压差减小，导致轮背轴向力F2的增大，而叶轮工作面轴向力F1基本不变，最终导致轴向力合力减小．

图9 叶轮轴向力简图

3.2 密封腔结构对泄漏量和轴向力的影响

迷宫密封腔结构直接决定了射流在空腔内部形成的涡流形态及强度，从而影响迷宫密封性能．图10为迷宫密封腔二维结构示意图．

图10 迷宫密封腔结构示意图

3.2.1 密封间隙 为研究密封间隙对SCO2向心涡轮轮背泄漏流的影响，建立4种密封间隙(s=0.13 mm，0.18 mm，0.20 mm，0.25 mm)的迷宫密封模型．不同间隙模型在相同设置条件下的泄漏量和轴向力计算结果如图11和12所示．

由图11可知，泄漏量随密封间隙线性增加．随着密封间隙增大，泄漏量逐渐增大，气体压力损失也随之增大，这与文献[13]的研究结果是一致的．泄漏量随着密封间隙的增大而增大的原因，可以分成两个方面：一方面，密封间隙增大，泄漏面积增大，工质直接流入下一个齿腔，未能形成强烈的射流，涡流流动减弱；另一方面，密封间隙增大，节流耗散作用减弱．在相同条件下，密封间隙越小，密封进出口压差反而越大，这表明泄漏量受密封间隙的影响更为显著．由图12可知随着密封间隙的增大，轴向力随之增大．在相同条件下，密封间隙越小，轮背空腔静压越大，而叶轮工作面轴向力F1变化不大．因此，在满足安全运行和生产工艺要求的前提下，应尽可能选择较小的密封间隙．

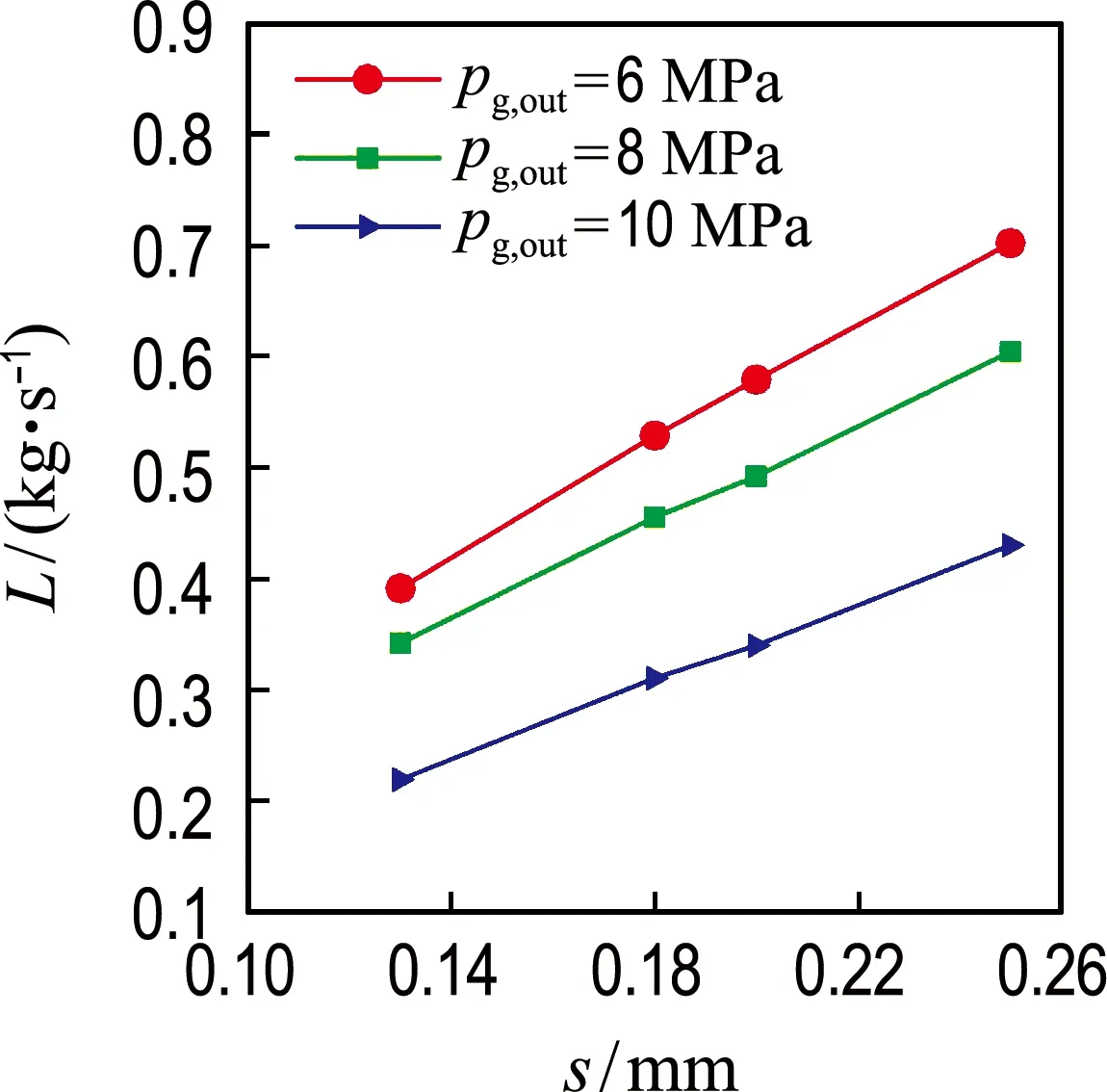
图11 泄漏量随密封间隙的变化曲线

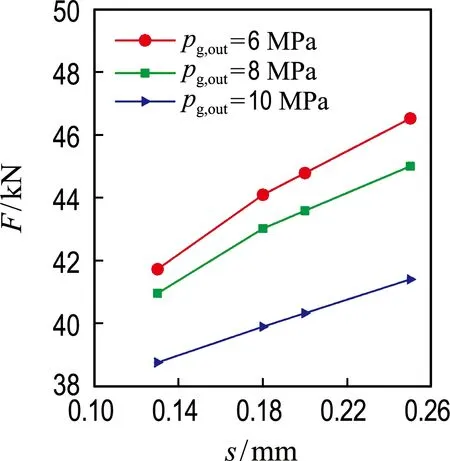
图12 轴向力随密封间隙的变化曲线

3.2.2 密封齿高 为研究密封齿高对SCO2向心涡轮轮背泄漏流的影响，建立8种密封齿高(h=0.9 mm，1.8 mm，2.7 mm，3.6 mm，4.5 mm，5.4 mm，6.3 mm，7.2 mm)的迷宫密封模型．不同密封齿高模型在相同设置条件下的泄漏量和轴向力计算结果如图13和14所示．

由图13可知，在密封齿高取值为1.8～5.4 mm 时，泄漏量线性减少；当密封齿高大于6.3 mm 时，泄漏量趋于稳定，达到相应压力、密封间隙下的最小值．造成这种情况的原因是，随着密封齿高的增大，迷宫密封内的流动在最后一个空腔内逐渐达到临界状态，出现流动堵塞，泄漏量不再随着密封齿高的增大而变化．由图14可知，随着密封齿高的增大，轴向力整体呈现减小的变化趋势．与泄漏量类似，当密封齿高大于6.3 mm时，轴向力基本保持不变．

图13 泄漏量随密封齿高的变化曲线

图14 轴向力随密封齿高的变化曲线

3.2.3 密封齿数 为探究密封齿数对SCO2向心涡轮轮背泄漏流的影响，本文建立4种密封齿数(n=4，5，6，7)的迷宫密封模型，计算其在密封出口静压分别为6、8、10 MPa时的泄漏量和轴向力．改变密封齿数有两种方案[14]：保持齿间距不变改变迷宫密封轴向长度(方案一)和保持迷宫密封轴向长度不变改变齿间距(方案二)．本文对上述两种方案都进行了数值模拟，其中方案一的齿间距设定为2.0 mm，方案二密封轴向长度设定为20 mm．

图15和16分别展示了基于方案一泄漏量和轴向力随密封齿数的变化情况．由图中的曲线可知，随着齿数的增加，泄漏量和轴向力随之减小，齿数为7时的密封效果最好．Kim等的研究[15]也证实了这一结论．

图15 不同齿数模型对应的泄漏量变化曲线(方案一)

图16 不同齿数模型对应的轴向力变化曲线(方案一)

Fig.16 Axial-force variation curve corresponding to different tooth number models (Scheme 1)

图17展示的是方案一的不同齿数模型速度矢量图和熵分布云图．由图17(a)～(d)可知，随着齿数的增加，齿腔中心的大涡面积不断扩大，流场分布更加均匀．迷宫密封的熵增主要分布在齿腔边角处．尤其当齿数为4时，熵增非常明显，密封效果差．随着齿数增加，熵增幅度减弱．而在齿数为7的模型中，熵的分布比较均匀，除了齿腔边角处的熵略有增加，这种情况下流体的动能通过湍流漩涡和摩擦等方式耗散为热能的效率较高，泄漏量最少．

图18和19分别展示了基于方案二泄漏量和轴向力随密封齿数的变化情况．观察图中曲线可得，与方案一类似，随着齿数的增加，泄漏量和轴向力都减小，齿数为6和7时密封效果基本相同．

图20展示的是方案二的不同齿数模型速度矢量图和熵分布云图．由图可知齿数为4的模型中熵增剧烈；随着齿数增加，密封腔内熵增减弱，6个齿腔模型的流场和熵分布与7个齿腔模型基本相同，密封效果相差不大．在实际的工程应用中，由于安装尺寸和结构布局等因素的制约，迷宫密封轴向长度及其结构形式是确定的，只能通过改变齿间距来调整密封齿数(即方案二)．对于本研究中的直角梯形齿形而言，设置6个齿腔可以实现最佳的密封效果．

(a) n=4

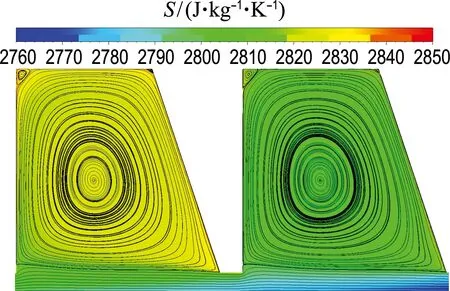
(b) n=5

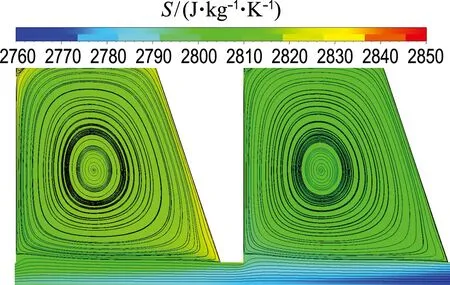
(c) n=6

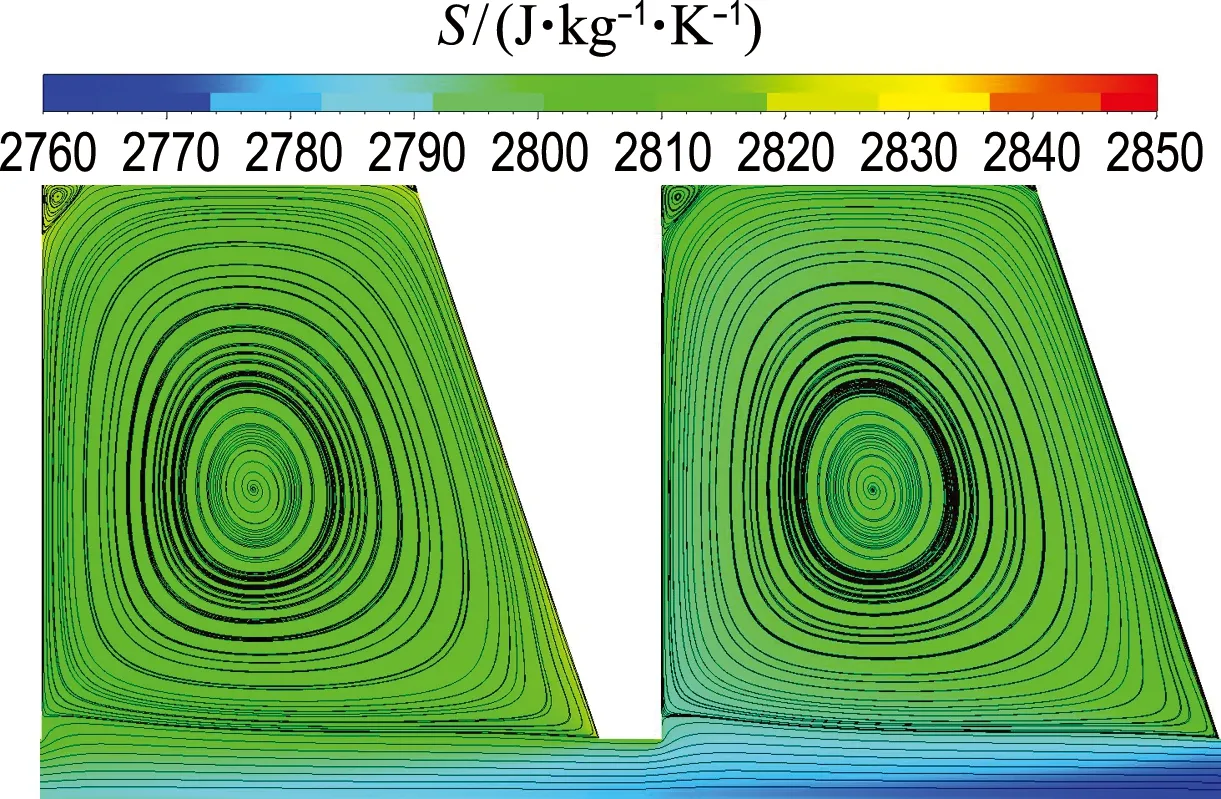
(d) n=7

图17 不同齿数模型速度矢量图和熵分布云图(方案一)

Fig.17 Velocity vector and entropy distribution cloud map for different tooth number models (Scheme 1)

图18 不同齿数模型对应的泄漏量变化曲线(方案二)

图19 不同齿数模型对应的轴向力变化曲线(方案二)

3.2.4 密封齿形 为研究齿形对SCO2向心涡轮轮背泄漏流的影响，建立4种齿形(三角形齿、矩形齿、直角梯形齿和等腰梯形齿)的迷宫密封模型，如图21所示．不同齿形模型在相同设置条件下的泄漏量和轴向力计算结果如图22和23所示．

由图22和23可知，等腰梯形齿密封效果最好，轴向力最小，直角梯形齿次之，紧接着是矩形齿，三角形齿的密封效果最差，轴向力最大．

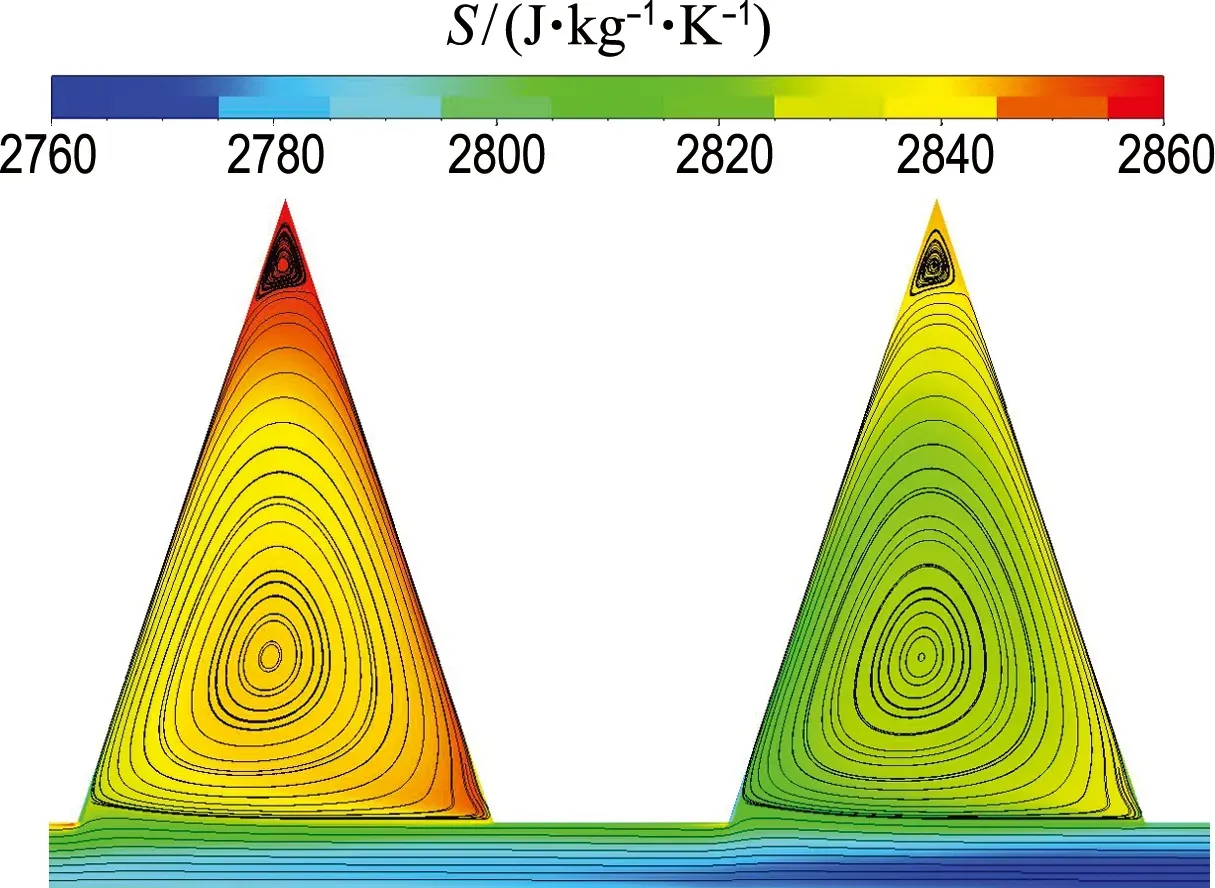
图24展示的是4种齿形对应的速度矢量图和熵分布云图．由图可知4种齿形的流场结构相似，均存在分布于齿腔中心的大涡流和边角处的小涡流以及齿尖处的分离涡流．另外，各齿形的流场仍存在一些差异．三角形齿腔的大涡流范围小，熵增明显；直角梯形齿的大涡流没有等腰梯形齿腔的大涡流发展的充分，且等腰梯形齿边角处存在更小范围的小涡流，熵的分布比较均匀；矩形齿腔中心的大涡流范围较大，但边角处的熵增显著．综上，等腰梯形齿密封性能最优．

(a) n=4

(b) n=5

(c) n=6

(d) n=7

图20 不同齿数模型速度矢量图和熵分布云图(方案二)

Fig.20 Velocity vector and entropy distribution cloud map for different tooth number models (Scheme 2)

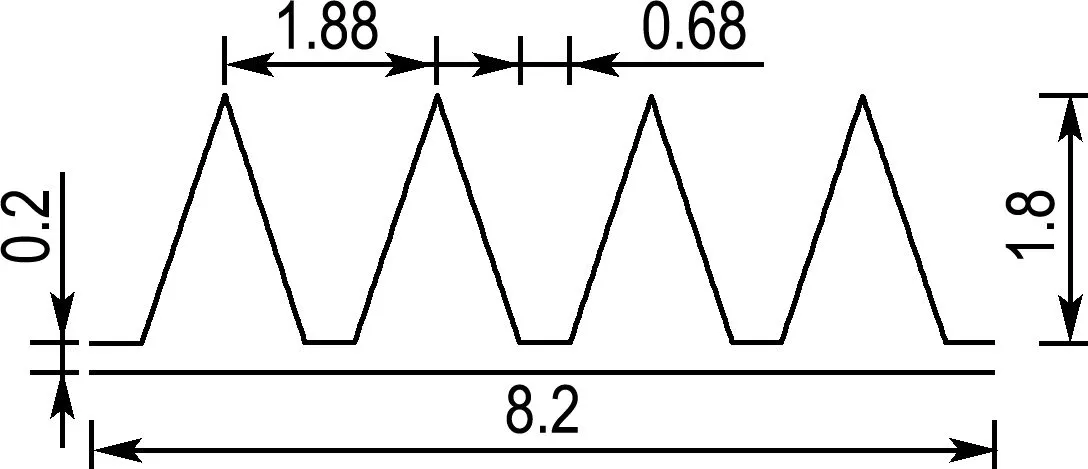
(a) 三角形齿

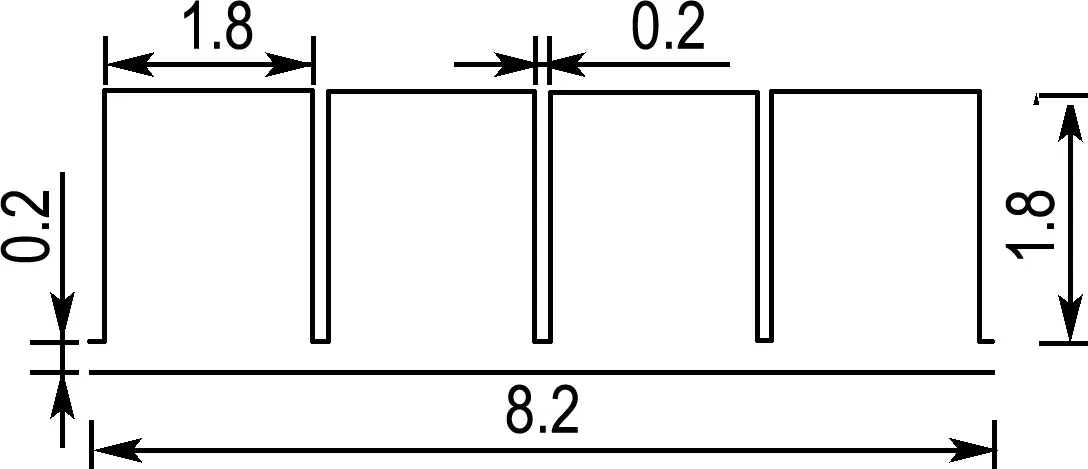
(b) 矩形齿

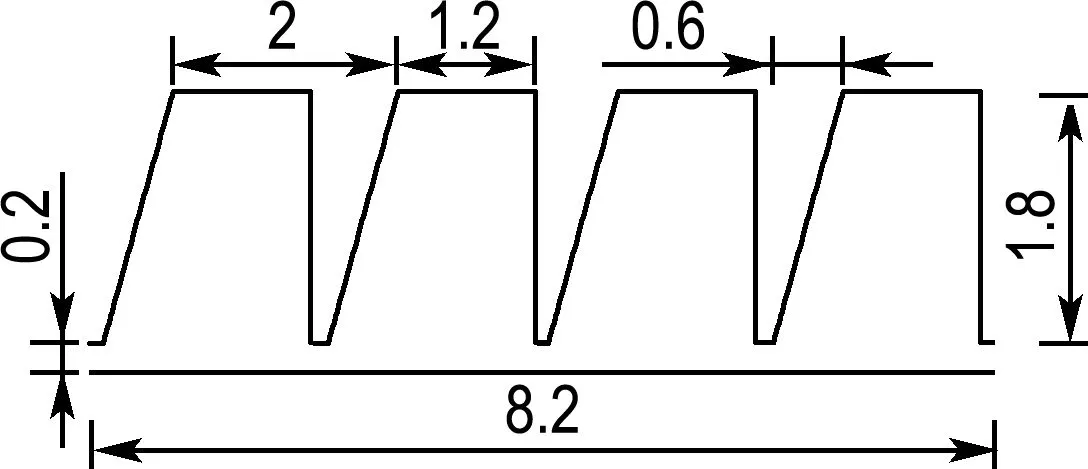
(c) 直角梯形齿

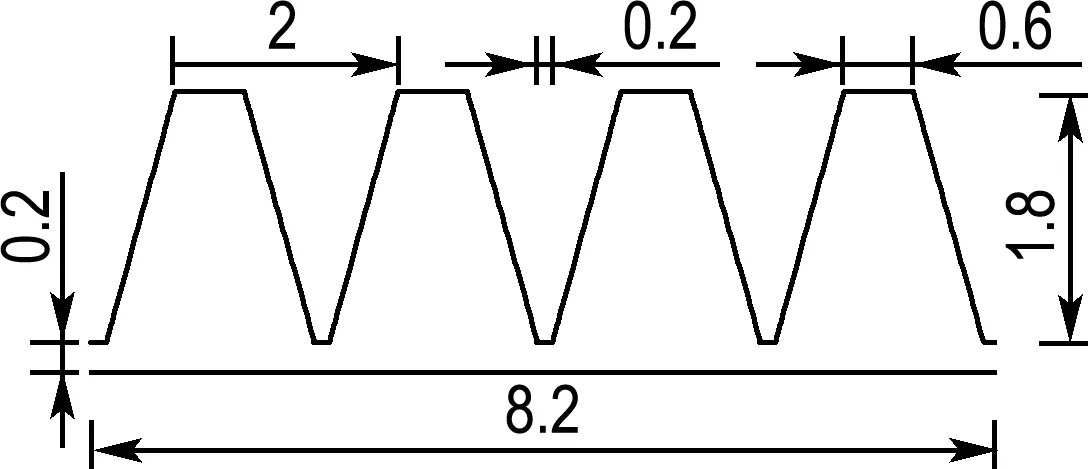
(d) 等腰梯形齿

图21 不同齿形的迷宫结构示意图(单位：mm)

Fig.21 Schematic diagram of the labyrinth structure of different tooth shapes (unit: mm)

图22 不同齿形泄漏量随密封出口静压变化曲线

图23 不同齿形轴向力随密封出口静压变化曲线

(a) 三角形

(b) 直角梯形

(d) 矩形

图24 不同齿形对应的速度矢量图和熵分布云图

Fig.24 Velocity vector and entropy distribution cloud map for different tooth shapes

4 结 论

(1)采用迷宫密封能够有效地改善轮背泄漏流，对于本文研究的某MW级SCO2向心涡轮，最大降低泄漏量为0.194 kg/s，最大降低轴向力为2.727 kN．涡轮的泄漏量和轴向力随着密封出口压力的增大而减小，与密封间隙呈正比变化趋势，在一定范围内随着密封齿高增大而近似线性减小，当密封齿高超过6.3 mm时，泄漏量和轴向力基本保持不变．

(2)大量的试验研究表明，随着密封齿数的改变，迷宫密封的泄漏量会发生变化．在密封轴向长度给定的情况下，合理地设置齿数能实现泄漏量和轴向力最小化，对于本文研究的直角梯形齿而言，齿数为6的模型具有最佳的密封效果．

(3)采用不同的密封齿形会产生不同的迷宫效应．本文中等腰梯形齿的密封性能优于直角梯形齿、三角形齿及矩形齿．