数学问题解决背后的脑科学

李晓东

小华和小明在同一个跑道上跑步，他们跑得一样快，但小华比小明后起跑。当小华跑了5圈时，小明跑了15圈。当小华跑到30圈时，小明跑了多少圈？对于这种本该用加法解决的问题，很多学生却错误地给出（15÷5）30=90（圈）的比例答案。

儿童在很小的时候就有了加法思维，如明白多与少的意思，懂得与同伴公平地分配零食和玩具，上小学后则进一步学习了加减运算。加法思维是基于绝对量的考量，比例思维是基于相对量的思考，要求同时对几个数量关系进行比较，比例思维比加法思维更为复杂与困难。儿童在小学低段就熟练地掌握了加减法，到6年级才学习比例，但为什么学生反而在加法上犯了比例错误呢？一种观点认为，这是由于问题的呈现形式造成的。比如，学生在学习比例推理时，遇到的问题总是以缺值形式呈现的，即在问题中，依次给出a、b、c三个数，要求求出第四个数x，使得a/b=c/x，或者a/c=b/x。学生在长期的练习中，错误地将这种问题呈现形式与比例推理建立了联结，形成了一种错误的直觉，即只要见到这种题型就会激活比例推理的方法。心理学上把这种错误的直觉叫启发式偏差。

人的大脑在加工信息时存在两种系统：一种是启发式系统，一种是分析式系统。前者是基于直觉的，其特点是快速、整体或全局的，无需努力。在很多情况下，这种策略是有效的，但有时会产生误导;后者则是缓慢、费力的，需要分析式策略，但总会得出正确答案。任何年龄的个体，在解决问题时，头脑里都是多种知识、多种策略并存并彼此竞争的。通常儿童和成人都会优先采用启发式策略，当启发式与问题冲突时，必须抑制住启发式的误导，才能启动分析式系统正确解决问题。

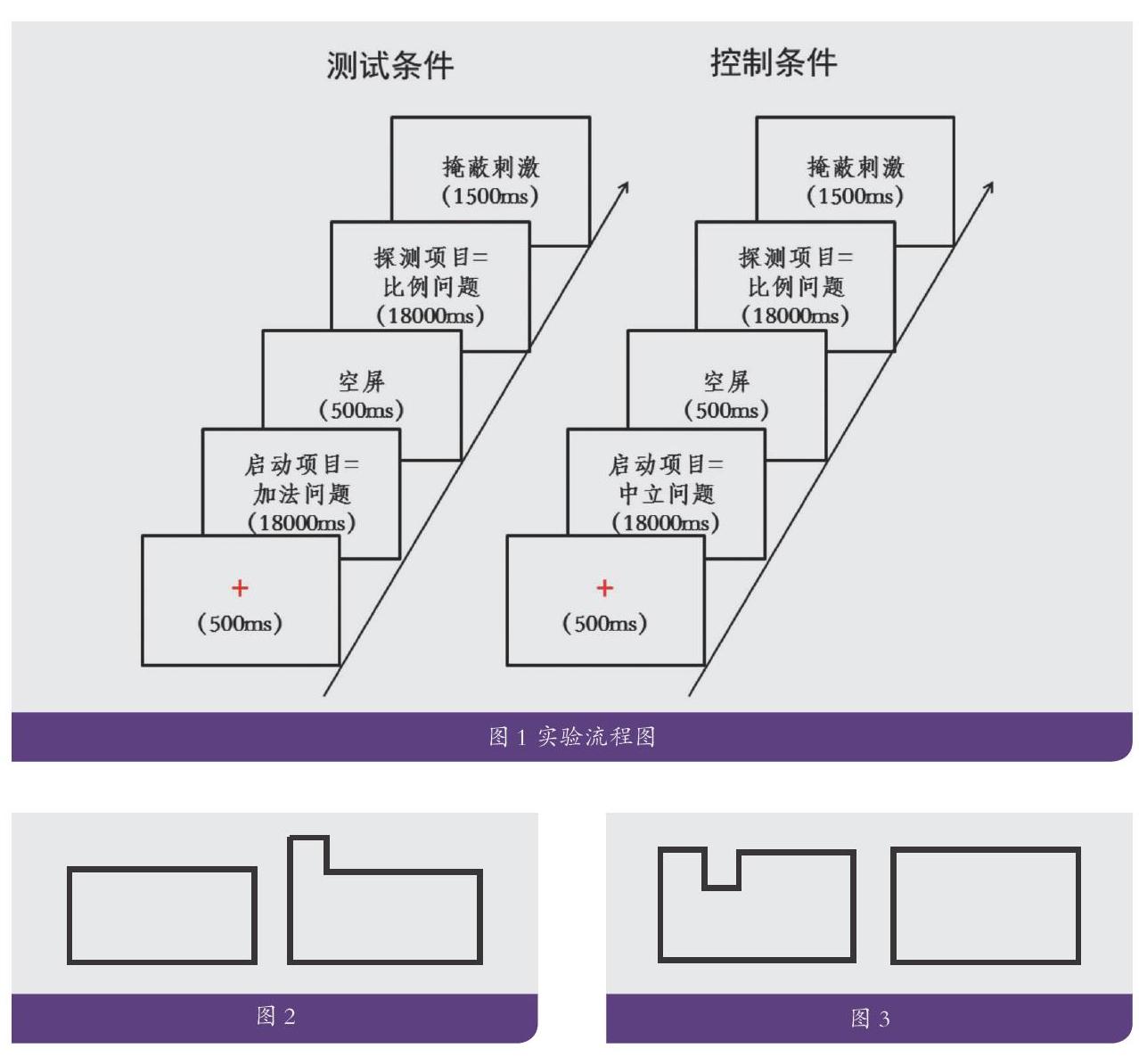
我们课题组采用负启动实验范式做过一项研究，实验流程（见图1）。负启动的实验逻辑是，如果在前一阶段需要抑制某种策略，那么在接下来的阶段需要重新激活该策略时则需要付出代价，表现为反应时的延长或错误率上升。该研究比较了大、中、小学生在两种条件下的表现：测试条件下先完成加法问题（启动项）再完成比例问题（探测项）;控制条件下先完成中立问题再完成比例问题。结果发现与控制条件相比，学生在测试条件下在比例问题上的错误率更高、反应时更长，说明要克服比例推理的误导需要抑制控制的参与。研究还发现，学生除了在缺值形式的加法问题上需要抑制比例策略外，在非符号的图片推理形式的加法任务上也同样需要抑制比例推理的误导。

先前知识的熟练掌握也可能成为一种误导性策略，从而干扰后续知识的学习。例如，在不同国家的学生中都发现了自然数偏差现象，即把自然数规则错误地迁移到有理数上。自然数偏差有三种，一种是大小比较，也叫整数偏差。如学生在学习分数时会误认为3/5 < 3/8，因为5<8; 学习小数时，误认为0.23>0.5，因为23>5，或者认为越长的小数越大。第二种是密度问题。自然数，数字是离散的、伪连续的，任意数字之后都有一个确切的数字，比如数字1后是数字2，数字2后接数字3。任意两个不相等自然数之间的数字个数是有限的，例如数字1和数字3之间，有且仅有一个自然数2。有理数是没有这个特性的，一个特定的有理数后面是没有确切的数的，而且两个有理数之间是有无数个数的。研究发现，学生对理解有理数的密度问题感到困难。例如，9年级的学生有一半以上的学生认为在3/8和5/8之间有一个数。第三种是算术运算偏差。对于自然数来说，加法和乘法运算总会使结果变得更大，进行减法和除法运算时，结果总会变得更小;但对于有理数，这条规则却不一定适用，如0.49<9 。我们最近的研究发現，学生比较不一致分数时（即分母大分数小）需要抑制自然数偏差的误导，表现为更长的反应时，脑电的研究也证明在比较不一致分数时需要抑制控制的参与。在判断有理数不等式是否成立时，也需要抑制“加法和乘法使结果变大，减法和除法使结果变小”的误导性策略。

此外，在其他一些数学问题上，学生也容易受到直觉的误导。学生常认为面积大的图形，其周长也长。我们设计了两种任务，一种是一致性任务，面积和周长协变，即面积大、周长长（如图2）;一种是不一致任务，面积大、周长小（如图3）。结果发现学生完成不一致任务时，需要抑制“面积大、周长长”的误导性策略。

学生在不一致任务上失败会不会是因为他们没有探测到问题与策略之间的冲突而不是抑制失败？为了回答这个问题，我们先让学生分别做一道一致题和一道不一致题，然后让他们对自己的答案做自信心判断。其逻辑是如果学生能够探测到冲突，那么当他们错误地使用了误导性策略时，相比于正确解答的情况其自信心会下降。结果发现在一致题上做对、不一致题做错的学生对于不一致题的自信是低于一致题的;而一致和不一致题都做对的学生对不一致题的自信是高于一致题的。说明学生是能够探测到冲突的，那些在不一致题目上正确的学生因为探测到了冲突对自己的答案就更加自信。因此，我们可以得出结论，学生之所以在不一致问题上失败，是因为他们不能有效抑制误导性策略或过度学习的知识。研究还发现，学生的工作记忆容量与学生解题的错误率是呈显著负相关的，这说明学生不能抑制启发式偏差可能与工作记忆资源不足有关。

这些研究表明，过度学习可能是一把双刃剑：一方面熟能生巧，遇到同类问题时可能会迅速解决问题;但是当眼前的问题与过去学习的内容只是表面相似而本质不同时，过度学习的知识就成为一种启发式偏差妨碍问题的解决。教师应了解抑制功能在学生学习过程中的重要性，抑制不仅意味着抵抗外源性的干扰，抑制头脑中的误导性知识与策略同样重要。同时，研究也表明对学生加强元认知、工作记忆等认知能力训练有助于克服启发式偏差。