等截面连续梁桥动力特性解析计算方法研究

郑玉平

（苏交科集团检测认证有限公司，南京211112）

1 引言

连续梁桥的频率特性一般只能通过有限元分析计算得到，建模分析工作量大。本文针对等截面连续梁桥，采用微分方程解析求解与超越方程数值求解相结合的方法，给出此类桥梁的动力特性解析解。

2 等截面连续梁桥自振频率求解

对如图1 所示的等跨、等截面连续梁结构，任取第s跨为分析对象，其第n阶振型函数以及振型函数对位置坐标的导数表示为方程式（1）～式（3）：

图1 连续梁示意图

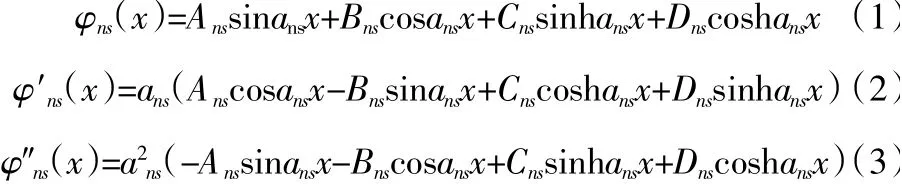
式中，渍ns为第n阶振型函数，渍忆ns为一阶导数、渍义ns为二阶导数；Ans、Bns、Cns、Dns、…为由边界条件决定的常数；an为频率参数。

以第s跨为对象，其振型函数以及相邻两跨的振型函数应满足以下边界条件：

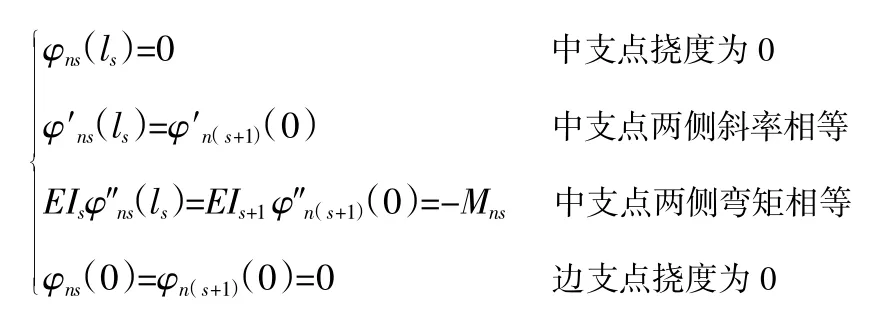
式中，E为弹性模量。

将振型函数及其导数代入上式边界条件，即可得到连续梁振型函数的边界方程：

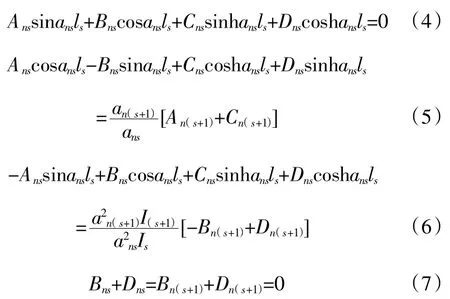
联立方程可得到第s跨的三弯矩方程（8）：

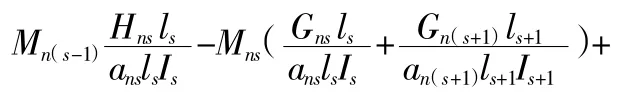
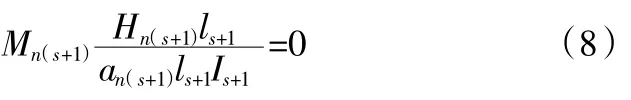
式中，Mn（s-1）、Mns、Mn（s+1）对应n阶s-1、s、s+1 连续支点处的弯矩。

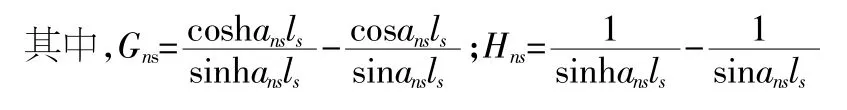
采用三弯矩方程构成一个联立方程组，方程组的解为结构按固有振型振动时节点弯矩。由于弯矩的任意性，要求方程组的系数行列式必须为零，这就构成了一个以Gns和Hns为未知数，或本质上以频率参数ansls为未知数的方程，即为连续梁的频率方程。表1 为等截面等跨径连续桥的频率方程。

表1 等截面等跨径连续梁桥的频率方程

采用数值方法进行求解，可得到相应的频率参数anl。将anl由小到大排列，可发现anl是按表1 中的频率方程排序顺次取值，并循环往复，部分结果如表2 所示。自振圆频率如下：

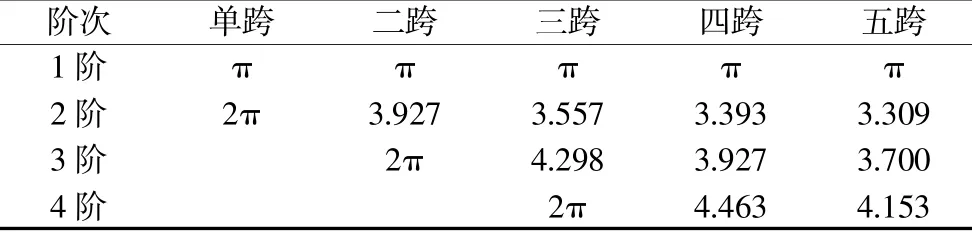
表2 等截面等跨径连续梁桥的部分频率参数al

连续梁桥随跨数的增加，其频率谱逐渐变得密集，此种频谱加密是由连续梁桥内支点的转动约束条件的不同引起。

3 等截面连续梁桥振型方程求解

随着桥跨数量的增加，连续梁桥的振型函数也变得更为复杂，但不同桥跨数量连续梁桥的振型函数之间存在着一定的联系。约定每一桥跨左支点x=0、右支点x=ls，本节将在此坐标体系下建立等截面、等跨径连续梁桥的振型方程。

设连续梁第i跨第n阶的振型方程如式（10）：

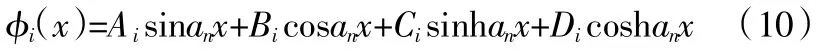
再次应用上文中给出的连续梁桥边界条件方程（4）～（7），可将振型方程中的4 个参数用单一变量描述，即为等截面连续梁桥的振型方程解析解。本文对常见跨径连续梁桥进行了求解。

对二跨连续梁桥：

1）第2n+1 阶振型（n=0，1，2，3，…），准1（x）=Aisinanx；准2（x）=-Aisinanx；

2）第2n+2 阶振型（n=0，1，2，3，…），准1（x）=（cosalsinaxcoshalsinhax）B2；

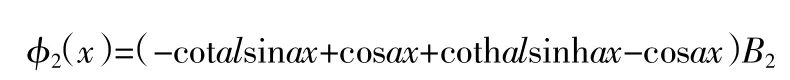
由于此二振型方程后文还会用到，为便于区分，记准*L（x）=准1（x）；准*R（x）=准2（x），二者为对称振型。

对于更多跨的连续梁桥，其振型也有固定的范式。两侧边跨振型方程为频率参数al的函数准*L（x）和准*R（x），二者形状关于连续梁中点对称，且函数形式与上式相同，并不随连续梁跨数的增加而改变。其余各中跨的振型准i（x）均可描述为两边跨振型的线性组合，即：

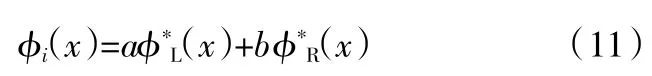
其中，准*L（x）=（cosalsinax-coshalsinhax）B2；准*R（x）=（-cotalsinax+cosax+cothalsinhax-cosax）B2；对于等跨径、等截面连续梁桥，无论截面尺寸、材料性质和跨径如何，a和b的数值均保持不变。此数值是由频率方程所决定的，只与结构边界条件和频率有关，对于常用跨径组合的系数a、b值汇总如表3 所示。

表3 连续梁桥振型组合系数（a，b）

4 结论

1）由于桥跨间约束的影响，相对于单跨简支梁桥，连续梁桥天然具有密集模态分布特性，在连续梁桥动力检测中应注意提高测试频域分辨率，避免频率遗漏。

2）等跨径、等截面连续梁桥的振型方程同样存在固定振动范式，中跨的振型方程可通过两边跨振型方程的线性叠加得到，叠加系数只与桥梁跨数有关。